Analysis of Free Vibration and Critical Buckling Load of Fiber Reinforced FGM Beams
-
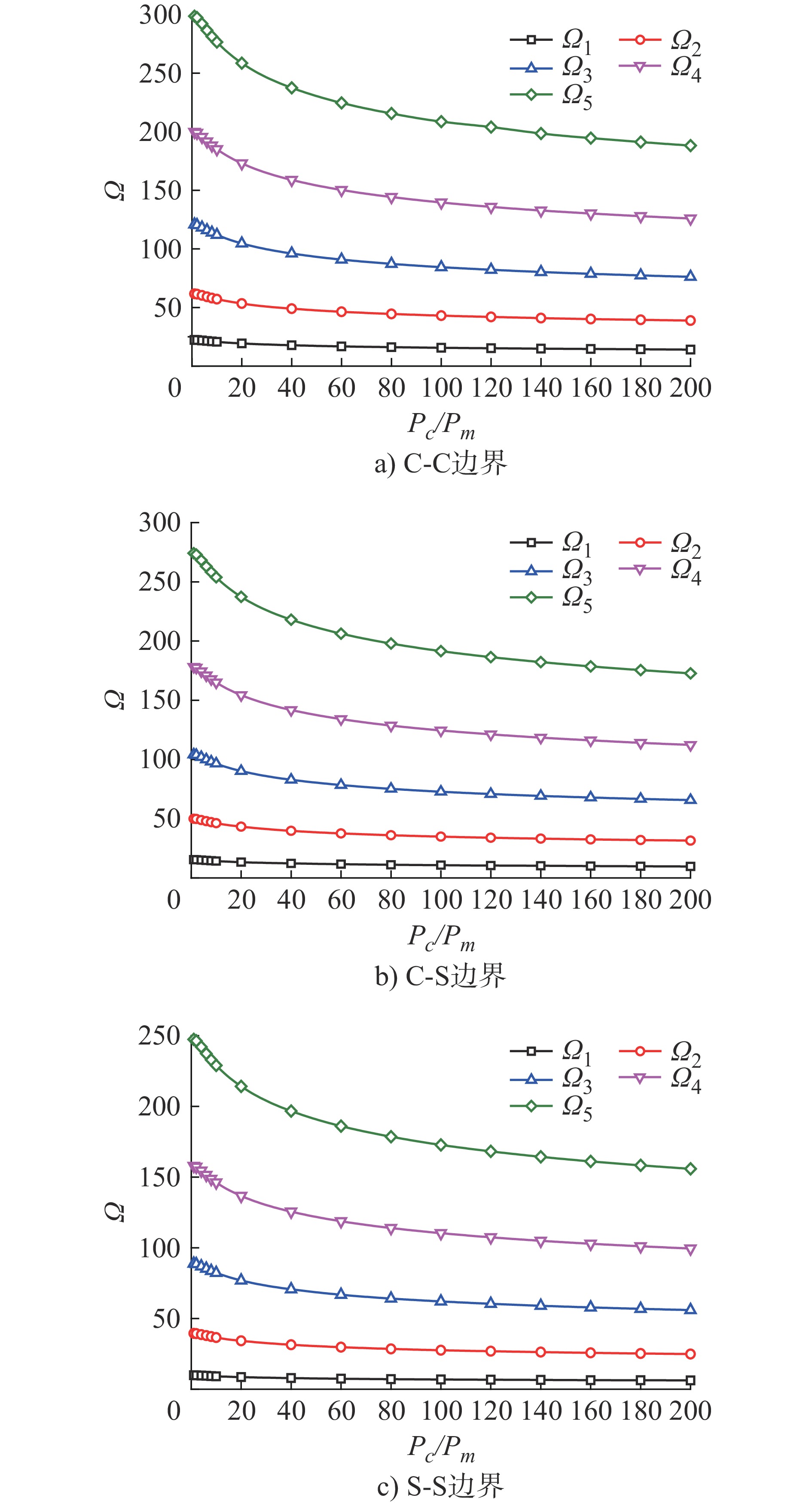
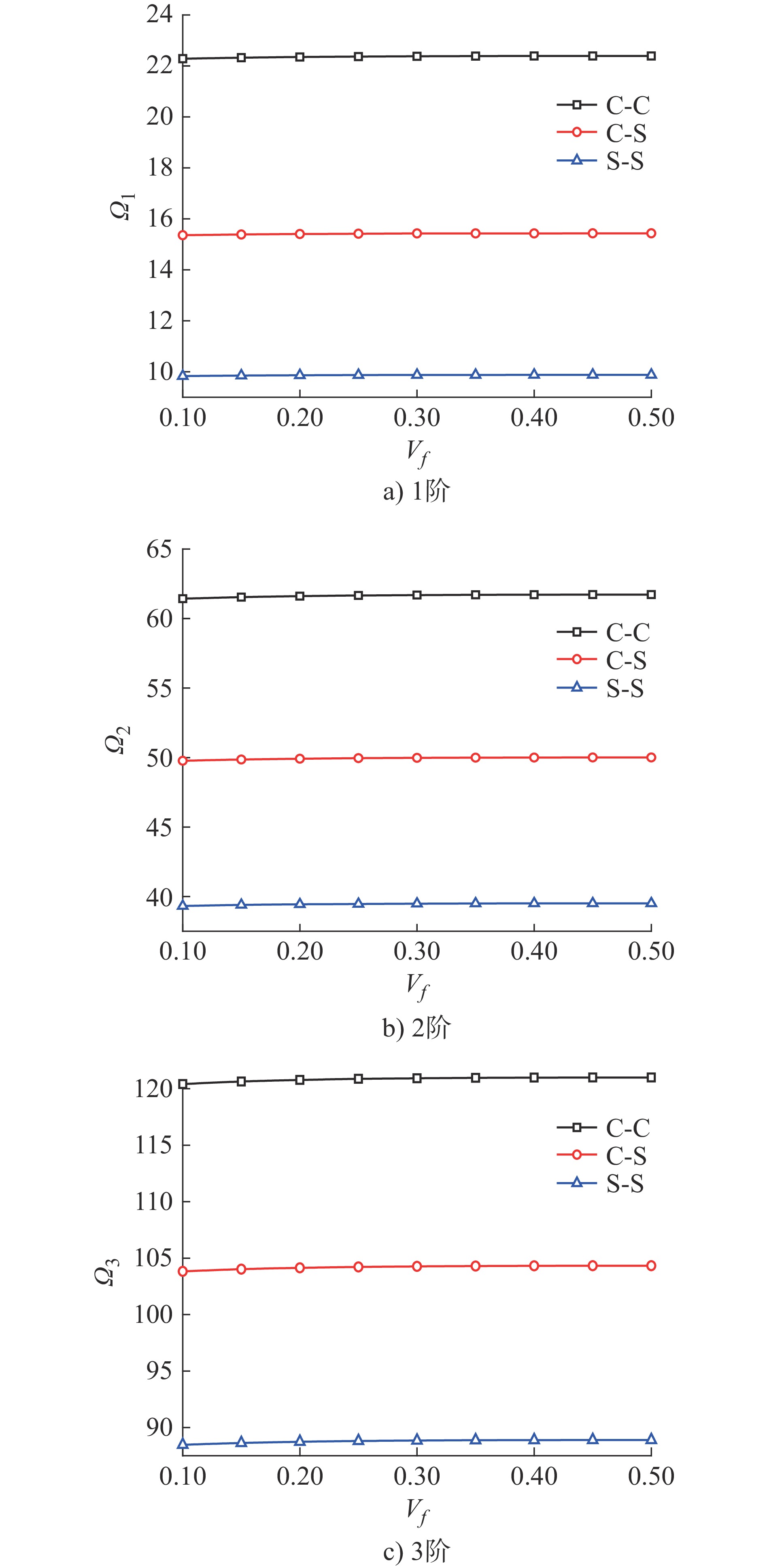
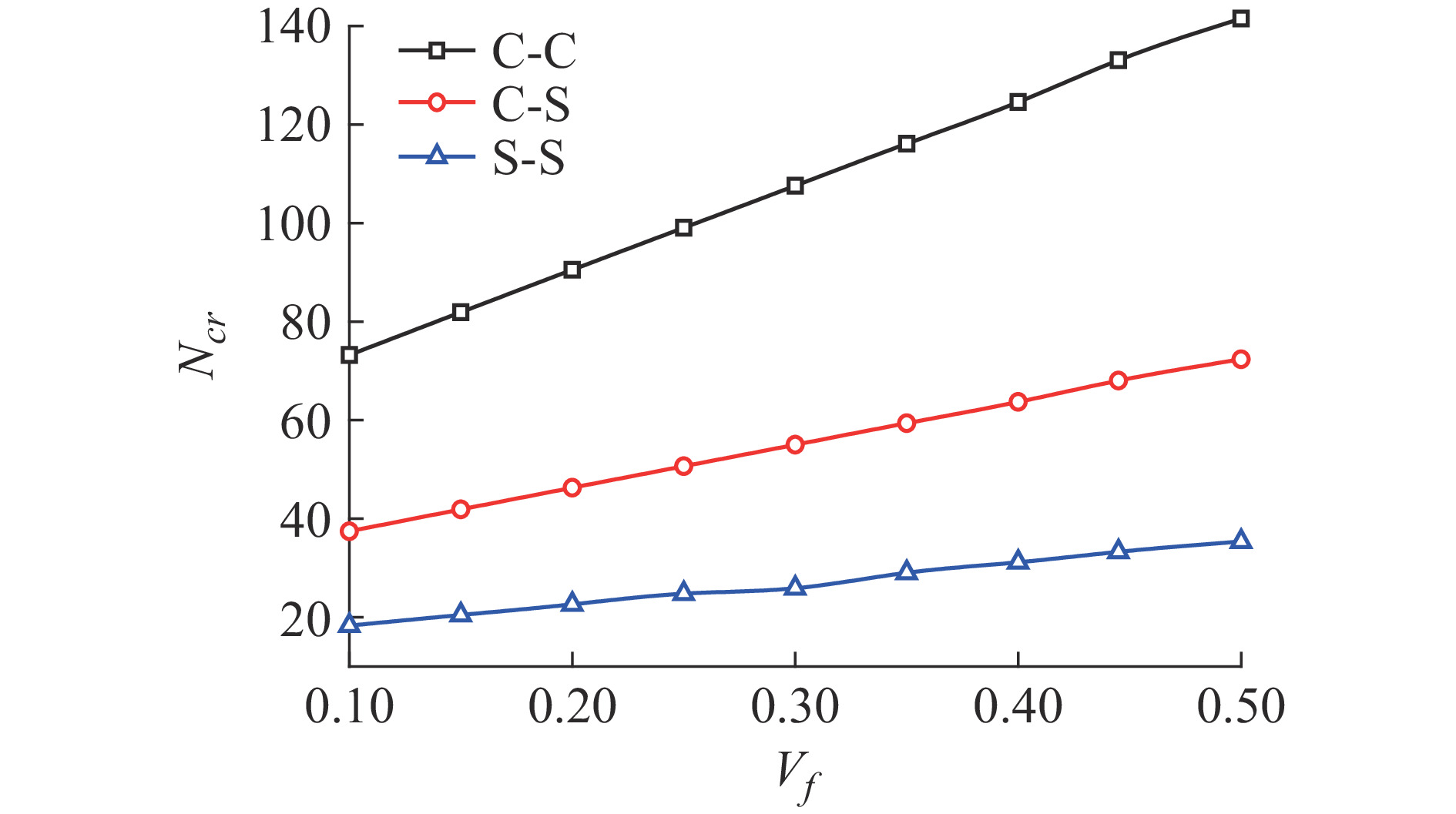
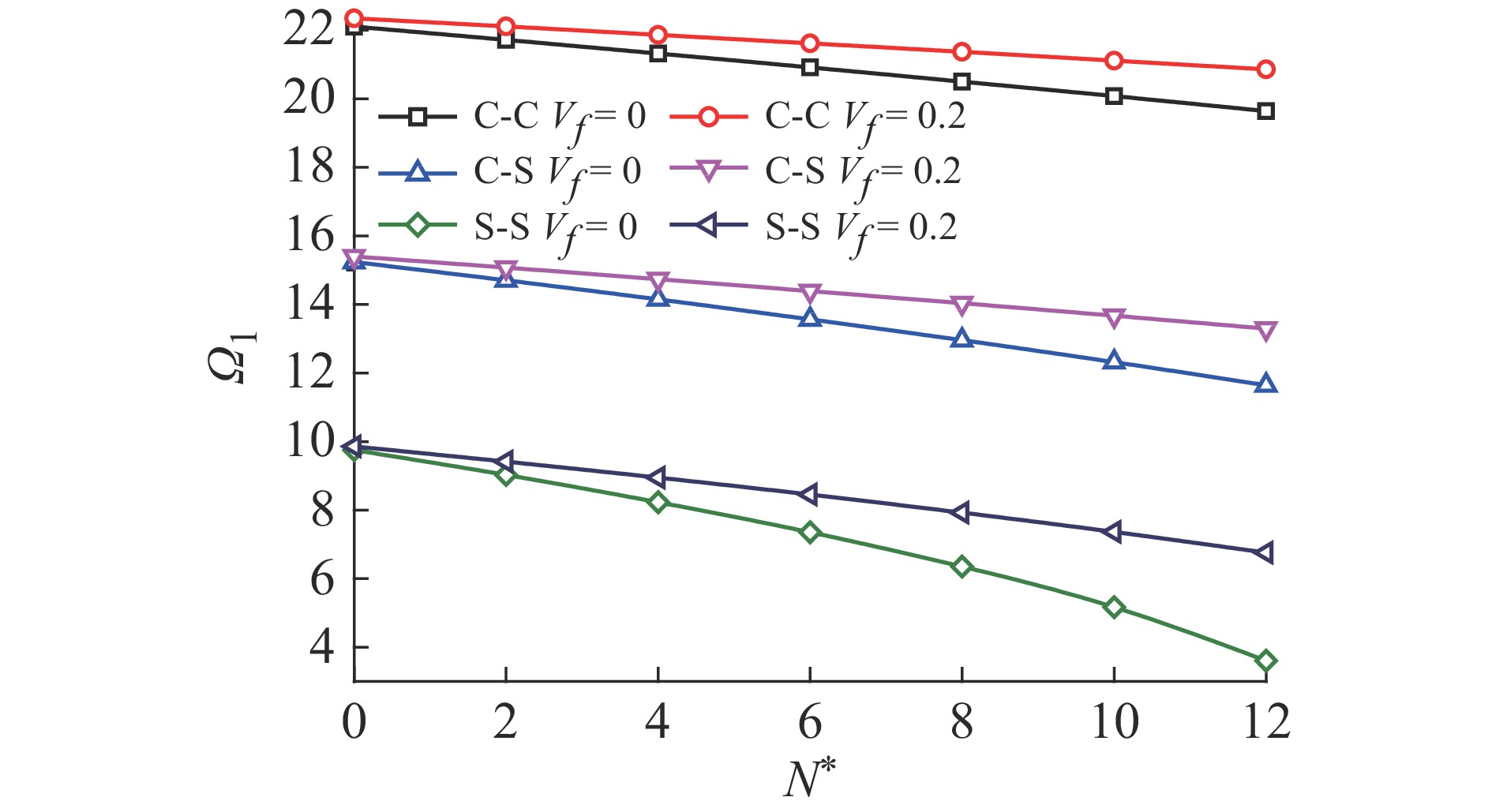
摘要: 基于经典梁理论(CBT)研究轴向力作用下纤维增强功能梯度材料(FGM)梁的横向自由振动和临界屈曲载荷问题。首先考虑由混合律模型来表征纤维增强FGM梁的材料属性,其次利用Hamilton原理推导轴向力作用下纤维增强FGM梁横向自由振动和临界屈曲载荷的控制微分方程,并应用微分变换法(DTM)对控制微分方程及边界条件进行变换,计算了纤维增强FGM梁在固定-固定(C-C)、固定-简支(C-S)和简支-简支(S-S)3种边界条件下横向自由振动的无量纲固有频率和无量纲临界屈曲载荷。退化为各向同性梁和FGM梁,并与已有文献结果进行对比,验证了本文方法的有效性。最后讨论在不同边界条件下纤维增强FGM梁的刚度比、纤维体积分数和无量纲压载荷对无量纲固有频率的影响以及各参数对无量纲临界屈曲载荷的影响。
-
关键词:
- 功能梯度材料梁 /
- 自由振动 /
- 固有频率 /
- 临界屈曲载荷 /
- 微分变换法 (DTM)
Abstract: Based on the classical beam theory (CBT), the transverse free vibration and critical buckling load of fiber reinforced functionally graded material (FGM) beams subjected to axial force are studied. Firstly, the mixing law model is considered to characterize the material properties of the fiber reinforced FGM beam. Secondly, the governing differential equations of transverse free vibration and critical buckling load of the fiber reinforced FGM beam subjected to axial force are derived by Hamilton principle, and the governing differential equations and boundary conditions are transformed by differential transformation method (DTM). The dimensional natural frequencies for transverse free vibration and dimensionless critical buckling loads of the fiber reinforced FGM beam are calculated under three boundary conditions of clamped-clamped (C-C), clamped-simply supported (C-S) and simply supported-simply supported (S-S). The problem is reduced to homogeneous material beams and FGM beams and compared with the existing literatures to verify its effectiveness. Finally, the effects of stiffness ratio, fiber volume fraction and dimensionless compressive load on the dimensionless natural frequency and all parameters on the dimensionless critical buckling load of the fiber reinforced FGM beam under different boundary conditions are discussed. -
表 1 不同边界条件各向同性材料梁的无量纲固有频率
表 2 不同边界条件下FGM梁无量纲固有频率
Pc/Pm Ω C-C C-S C-S 本文解 文献[21] 本文解 文献[21] 本文解 文献[21] Ω1 22.1080 22.108 15.2354 15.235 9.7526 9.7525 2 Ω2 60.9416 60.942 49.3725 49.373 39.0113 39.010 Ω3 119.4699 119.47 103.0117 103.01 87.7733 87.773 Ω1 21.7197 21.720 14.9678 14.968 9.5813 9.5813 3 Ω2 59.8711 59.871 48.5052 48.505 38.3251 38.325 Ω3 117.3713 117.37 101.2022 101.20 86.2315 86.231 Ω1 21.3518 21.352 14.7143 14.714 9.4190 9.4190 4 Ω2 58.8571 58.857 47.6837 47.684 37.676 37.676 Ω3 115.3834 115.38 99.4882 99.488 84.7710 84.771 Ω1 21.0199 21.020 14.4856 14.486 9.2726 9.2726 5 Ω2 57.9424 57.941 46.9427 46.942 37.0905 37.090 Ω3 113.5903 113.59 97.9421 97.942 83.4536 83.454 -
[1] 张鹏. 纤维增强功能梯度材料梁静态力学行为分析[D]. 扬州: 扬州大学, 2012ZHANG P. Analysis of the static mechanical behavior of fiber-reinforced functionally graded material beams[D]. Yangzhou: Yangzhou University, 2012 (in Chinese) [2] 衡亚洲. 弹性地基上正交各向异性矩形板自由振动与屈曲的DTM求解[D]. 兰州: 兰州理工大学, 2017HENG Y Z. Free vibration and buckling analysis of orthotropic rectangular plates resting on elastic foundations by using DTM[D]. Lanzhou: Lanzhou University of Technology, 2017 (in Chinese) [3] REDDY J N, CHIN C D. Thermomechanical analysis of functionally graded cylinders and plates[J]. Journal of Thermal Stresses, 1998, 21(6): 593-626 doi: 10.1080/01495739808956165 [4] WATTANASAKULPONG N, BUI T Q. Vibration analysis of third-order shear deformable FGM beams with elastic support by Chebyshev collocation method[J]. International Journal of Structural Stability and Dynamics, 2018, 18(5): 1850071 doi: 10.1142/S0219455418500712 [5] EBRAHIMI F, GHADIRI M, SALARI E, et al. Application of the differential transformation method for nonlocal vibration analysis of functionally graded nanobeams[J]. Journal of Mechanical Science and Technology, 2015, 29(3): 1207-1215 doi: 10.1007/s12206-015-0234-7 [6] GHAZARYAN D, BURLAYENKO V N, AVETISYAN A, et al. Free vibration analysis of functionally graded beams with non-uniform cross-section using the differential transform method[J]. Journal of Engineering Mathematics, 2018, 110(1): 97-121 doi: 10.1007/s10665-017-9937-3 [7] BAGHLANI A, KHAYAT M, DEHGHAN S M. Free vibration analysis of FGM cylindrical shells surrounded by Pasternak elastic foundation in thermal environment considering fluid-structure interaction[J]. Applied Mathematical Modelling, 2020, 78: 550-575 doi: 10.1016/j.apm.2019.10.023 [8] 滕兆春, 昌博, 付小华. 弹性地基上转动功能梯度材料Timoshenko梁自由振动的微分变换法求解[J]. 中国机械工程, 2018, 29(10): 1147-1152 doi: 10.3969/j.issn.1004-132X.2018.10.003TENG Z C, CHANG B, FU X H. DTM analysis for free vibrations of rotating functionally graded material Timoshenko beams on elastic foundations[J]. China Mechanical Engineering, 2018, 29(10): 1147-1152 (in Chinese) doi: 10.3969/j.issn.1004-132X.2018.10.003 [9] 林鹏程, 滕兆春. 热冲击下轴向运动FGM梁的自由振动分析[J]. 振动与冲击, 2020, 39(12): 249-256LIN P C, TENG Z C. Free vibration analysis of axially moving FGM beams under thermal shock[J]. Journal of Vibration and Shock, 2020, 39(12): 249-256 (in Chinese) [10] GUPTA A, TALHA M, SEEMANN W. Free vibration and flexural response of functionally graded plates resting on Winkler-Pasternak elastic foundations using nonpolynomial higher-order shear and normal deformation theory[J]. Mechanics of Advanced Materials and Structures, 2018, 25(6): 523-538 doi: 10.1080/15376494.2017.1285459 [11] 蒋伟男, 郝育新, 吕梅. 几种边界条件下功能梯度夹层板自由振动分析[J]. 北京信息科技大学学报, 2020, 35(1): 15-22JIANG W N, HAO Y X, LYU M. Free vibration analysis of functional gradient sandwich plates under several boundary conditions[J]. Journal of Beijing Information Science & Technology University, 2020, 35(1): 15-22 (in Chinese) [12] 李万春, 滕兆春. 变曲率FGM拱的面内自由振动分析[J]. 振动与冲击, 2017, 36(9): 201-208LI W C, TENG Z C. In-plane free vibration analysis of FGM arches with variable curvature[J]. Journal of Vibration and Shock, 2017, 36(9): 201-208 (in Chinese) [13] 贺丹, 门亮. 碳纳米管增强型复合材料功能梯度板的自由振动模型与尺度效应[J]. 计算力学学报, 2018, 35(3): 326-330 doi: 10.7511/jslx20161028004HE D, MEN L. A free vibration model of carbon nanotube-reinforced functionally graded composite plates and scale effects[J]. Chinese Journal of Computational Mechanics, 2018, 35(3): 326-330 (in Chinese) doi: 10.7511/jslx20161028004 [14] 李晓倩, 宋敉淘. 温度场下石墨烯增强功能梯度梁的主共振行为分析[J]. 河南科技大学学报(自然科学版), 2019, 40(1): 66-71LI X Q, SONG M T. Primary resonance of functionally graded graphene-reinforced nanocomposite beams in thermal environments[J]. Journal of Henan University of Science and Technology (Natural Science), 2019, 40(1): 66-71 (in Chinese) [15] NEJATI M, FARD K M, ESLAMPANAH A, et al. Free vibration analysis of reinforced composite functionally graded plates with steady state thermal conditions[J]. Latin American Journal of Solids and Structures, 2017, 14(5): 886-905 doi: 10.1590/1679-78253705 [16] SHEN H S, XIANG Y. Nonlinear analysis of nanotube-reinforced composite beams resting on elastic foundations in thermal environments[J]. Engineering Structures, 2013, 56: 698-708 doi: 10.1016/j.engstruct.2013.06.002 [17] YAS M H, SAMADI N. Free vibrations and buckling analysis of carbon nanotube-reinforced composite Timoshenko beams on elastic foundation[J]. International Journal of Pressure Vessels and Piping, 2012, 98: 119-128 doi: 10.1016/j.ijpvp.2012.07.012 [18] THOMAS B, INAMDAR P, ROY T, et al. Finite element modeling and free vibration analysis of functionally graded nanocomposite beams reinforced by randomly oriented carbon nanotubes[J]. International Journal on Theoretical and Applied Research in Mechanical Engineering, 2013, 2(4): 97-102 [19] DING K, WENG G J. The influence of moduli slope of a linearly graded matrix on the bulk moduli of some particle- and fiber-reinforced composites[J]. Journal of Elasticity, 1999, 53(1): 1-22 [20] CLYNE T W, HULL D. An Introduction to Composite Materials[M]. 3rd ed. New York: Cambridge University Press, 2019 [21] BOUAMAMA M, ELMEICHE A, ELHENNANI A, et al. Exact solution for free vibration analysis of FGM beams[J]. Revue des Composites et des Matériaux Avancés-Journal of Composite and Advanced Materials, 2020, 30(2): 55-60 -







 下载:
下载: