Stochastic Model Updating Combining Cokriging Model and Single Objective Function
-
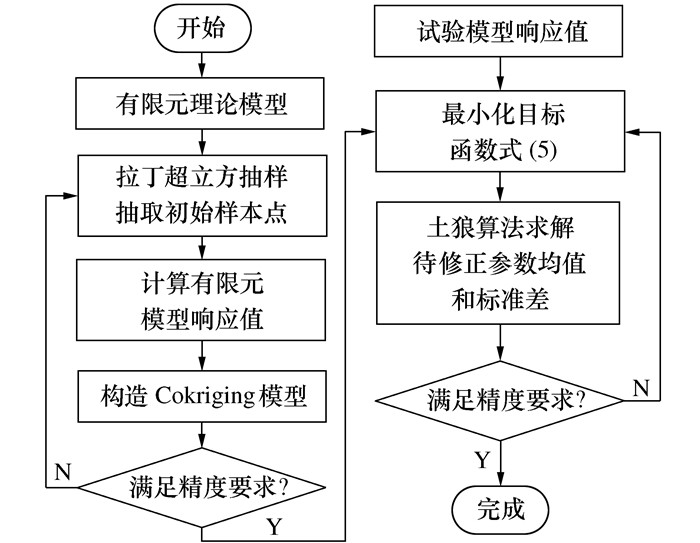
摘要: 将Cokriging代理模型技术和单目标函数进行结合,提出了一种随机模型修正方法。该方法将不确定性模型修正问题转化为较简单的待修正参数统计特征的修正问题,能够在保证模型修正精度的同时,有效缓解模型修正中由于分步修正和多目标修正造成的计算成本高的问题。首先,假设待修正参数和响应均服从高斯分布,采用拉丁超立方抽样获取训练集样本,构造满足精度要求的Cokriging模型以替代复杂的有限元模型参与迭代计算。然后,建立有限元模型计算响应统计特征与试验响应统计特征的加权残差目标函数,引入土狼优化算法最小化该单目标函数来得到待修正参数的统计特征。最后,通过二维和三维桁架结构验证了所提方法的可行性。
-
关键词:
- 不确定性 /
- 模型修正 /
- 单目标函数 /
- 全局优化 /
- Cokriging模型
Abstract: A stochastic model updating method is proposed by combining the Cokriging surrogate model technique with the single objective function. The method transforms the uncertainty model updating problem into a simple updating problem of the statistical characteristics of the parameters to be updated, which can effectively alleviate the high computational cost problem caused by the stepwise and multi-objective updating while ensuring the updating accuracy. Firstly, assuming that the parameters to be updated and the corresponding responses obey Gaussian distribution, the Latin hypercube sampling is used to obtain the training set samples, and the Cokriging model satisfying the accuracy requirement is constructed to replace the complex finite element model in the iterative calculation. Then, the weighted residual objective function between the statistical characteristics of the finite element model calculated responses and the statistical characteristics of the test responses is established, and the coyote optimization algorithm is introduced to minimize the single objective function to obtain the statistical characteristics of the parameters to be updated. Finally, the feasibility of the proposed method is verified by the two-dimensional and the three-dimensional truss structures.-
Key words:
- uncertainty /
- model updating /
- single objective function /
- global optimization /
- Cokriging model
-
表 1 修正前后结构参数均值与标准差(二维桁架)
Table 1. The mean and standard deviation of structural parameters before and after updating(2D truss)
修正参数 试验值 有限元值 修正前误差/% 多目标修正结果 单目标修正结果 修正值 相对误差/% 修正值 相对误差/% E1均值/GPa 190 209 10 190.006 3.16×10-3 190.099 5.21×10-2 E2均值/GPa 210 231 10 209.988 5.71×10-3 209.817 8.71×10-2 d均值/(kg·m-3) 7 800 7 020 -10 7 799.936 8.21×10-4 7 801.184 1.52×10-2 E1标准差 2.5 - - 2.622 4.88 2.581 3.24 E2标准差 2.2 - - 2.103 4.41 2.225 1.14 d标准差 25.0 - - 24.855 0.58 25.828 3.31 表 2 三维桁架模型属性
Table 2. Properties of 3D truss model
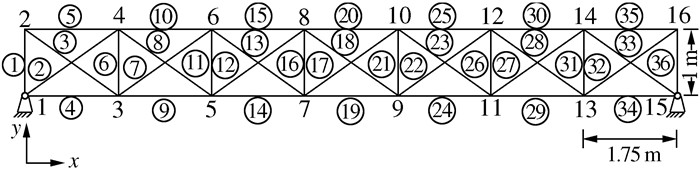
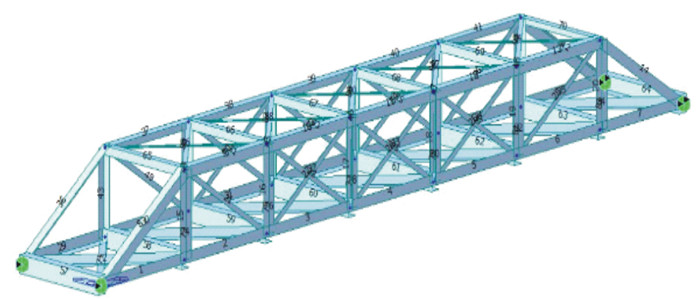
总重 节长 跨长 主桁中心距 跨高比 桁高 泊松比 杆单元 节点 54 kg 0.4 m 2.8 m 0.36 m 10 0.27 m 0.3 94个 28个 表 3 修正前后结构参数均值与标准差(三维桁架)
Table 3. The mean and standard deviation of structural parameters before and after updating(3D truss)
修正参数 试验值 有限元值 修正前误差/% 多目标优化 单目标优化 修正值 相对误差/% 修正值 相对误差/% E1均值/GPa 230 253 10 229.406 0.258 229.638 0.157 E2均值/GPa 210 189 -10 210.910 0.433 210.320 0.152 d均值/(kg·m-3) 7 300 8 030 10 7 305.604 7.68×10-2 7 300.361 4.95×10-3 E1标准差 3.0 - - 2.949 1.70 2.904 3.20 E2标准差 2.0 - - 2.089 4.45 2.003 0.15 d标准差 20.0 - - 20.400 2.00 20.473 2.36 -
[1] SIMOEN E, DE ROECK G, LOMBAERT G. Dealing with uncertainty in model updating for damage assessment: a review[J]. Mechanical Systems and Signal Processing, 2015, 56-57: 123-149. doi: 10.1016/j.ymssp.2014.11.001 [2] MOTTERSHEAD J E, LINK M, FRISWELL M I. The sensitivity method in finite element model updating: a tutorial[J]. Mechanical Systems and Signal Processing, 2011, 25(7): 2275-2296. doi: 10.1016/j.ymssp.2010.10.012 [3] 严海, 马锐磊, 梁跃, 等. 基于模态参数的水下航行器楔环结构有限元模型修正[J]. 鱼雷技术, 2016, 24(2): 87-93.YAN H, MA R L, LIANG Y, et al. Finite element model correction for wedged-ring connection structure of underwater vehicle based on modal parameters[J]. Torpedo Technology, 2016, 24(2): 87-93. (in Chinese) [4] 冷建成, 田洪旭, 徐爽, 等. 基于优化Kriging模型的平台结构动力学模型修正[J]. 振动与冲击, 2019, 38(18): 19-23.LENG J C, TIAN H X, XU S, et al. Dynamics model updating of an offshore platform structure based on optimized Kriging model[J]. Journal of Vibration and Shock, 2019, 38(18): 19-23. (in Chinese) [5] GOVERS Y, BÖSWALD M, FVLLEKRUG U, et al. Analysis of sources and quantification of uncertainty in experimental modal data[C]//International Conference on Noise & Vibration Engineering, Proceedings of ISMA2006. KU Leuven, Belgium, 2006: 4161-4173. [6] HUANG B, CHEN H. A new approach for stochastic model updating using the hybrid perturbation-Garlekin method[J]. Mechanical Systems and Signal Processing, 2019, 129: 1-19. doi: 10.1016/j.ymssp.2019.04.012 [7] MOENS D. Uncertainties in structural dynamics[J]. Mechanical Systems and Signal Processing, 2012, 32: 1-4. doi: 10.1016/j.ymssp.2012.07.011 [8] 宗周红, 高铭霖, 夏樟华. 基于健康监测的连续刚构桥有限元模型确认(Ⅱ)-不确定性分析与模型精度评价[J]. 土木工程学报, 2011, 44(3): 85-92.ZONG Z H, GAO M L, XIA Z H. Finite element model validation of the continuous rigid frame bridge based on structural health monitoring-Part Ⅱ: uncertainty analysis and evaluation of model accuracyⅡ[J]. China Civil Engineering Journal, 2011, 44(3): 85-92. (in Chinese) [9] HUA X G, NI Y Q, CHEN Z Q, et al. An improved perturbation method for stochastic finite element model updating[J]. International Journal for Numerical Methods in Engineering, 2008, 73(13): 1845-1864. doi: 10.1002/nme.2151 [10] FANG S E, ZHANG Q H, REN W X. Parameter variability estimation using stochastic response surface model updating[J]. Mechanical Systems and Signal Processing, 2014, 49(1-2): 249-263. doi: 10.1016/j.ymssp.2014.04.017 [11] 陈炉云, 杨念. 基于多层次权重系数的结构动力学模型修正[J]. 上海交通大学学报, 2017, 51(12): 1415-1421.CHEN L Y, YANG N. Model updating analysis of structural dynamic problem based on multi-level weight coefficients[J]. Journal of Shanghai Jiaotong University, 2017, 51(12): 1415-1421. (in Chinese) [12] 陈辉, 张衡, 李烨君, 等. 测量模态不确定的梁式结构随机有限元模型修正[J]. 振动工程学报, 2019, 32(4): 653-659.CHEN H, ZHANG H, LI Y J, et al. Stochastic finite element model updating of beam structure based on uncertain measurement modes[J]. Journal of Vibration Engineering, 2019, 32(4): 653-659. (in Chinese) [13] 秦仙蓉, 詹澎明, 赵书振, 等. 基于替代模型的岸桥随机有限元模型修正[J]. 振动与冲击, 2020, 39(1): 43-48.QIN X R, ZHAN P M, ZHAO S Z, et al. Updating of stochastic finite element model of a quayside container crane based on meta-model[J]. Journal of Vibration and Shock, 2020, 39(1): 43-48. (in Chinese) [14] 崔逊学. 多目标进化算法及其应用[M]. 北京: 国防工业出版社, 2006.CUI X X. Multiobjective evolutionary algorithms and their applications[M]. Beijing: National Defense Industry Press, 2006. (in Chinese) [15] LAURENT L, BOUCARD P A, SOULIER B. Generation of a cokriging metamodel using a multiparametric strategy[J]. Computational Mechanics, 2013, 51(2): 151-169. [16] PIEREZAN J, DOS SANTOS COELHO L. Coyote optimization algorithm: a new metaheuristic for global optimization problems[C]//Proceedings of 2018 IEEE Congress on Evolutionary Computation. Rio de Janeiro, Brazil: IEEE, 2018. -







 下载:
下载: