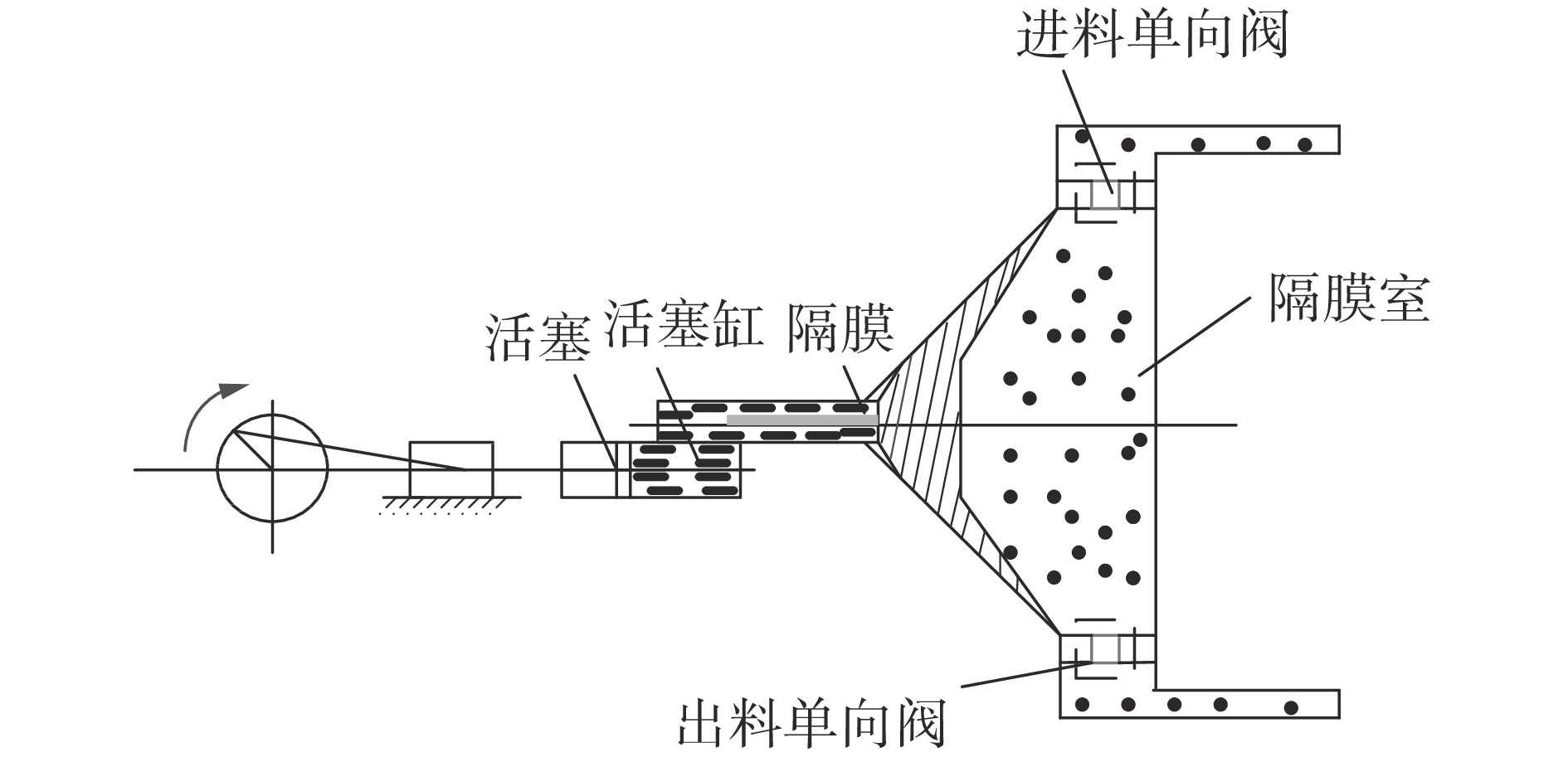
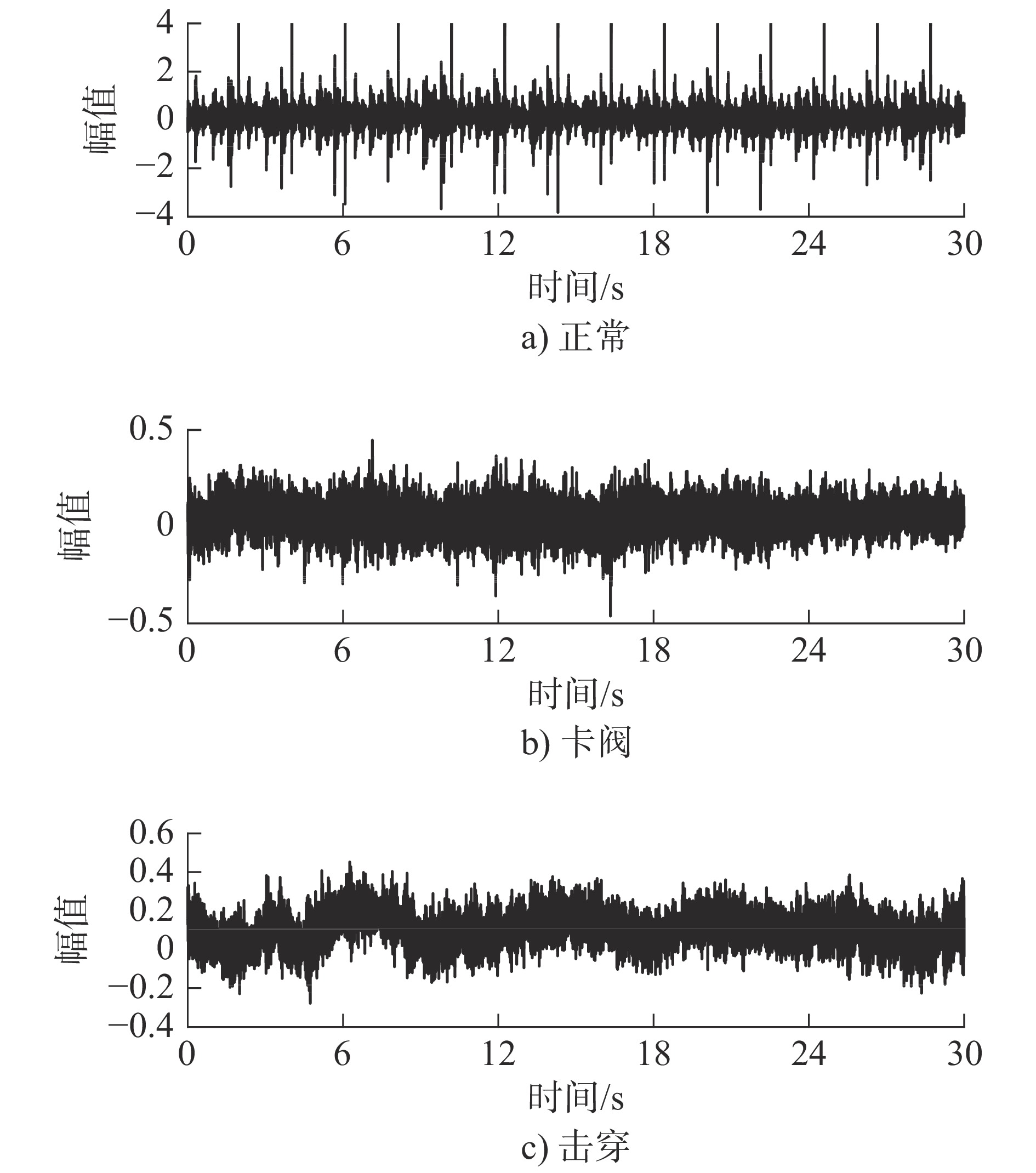
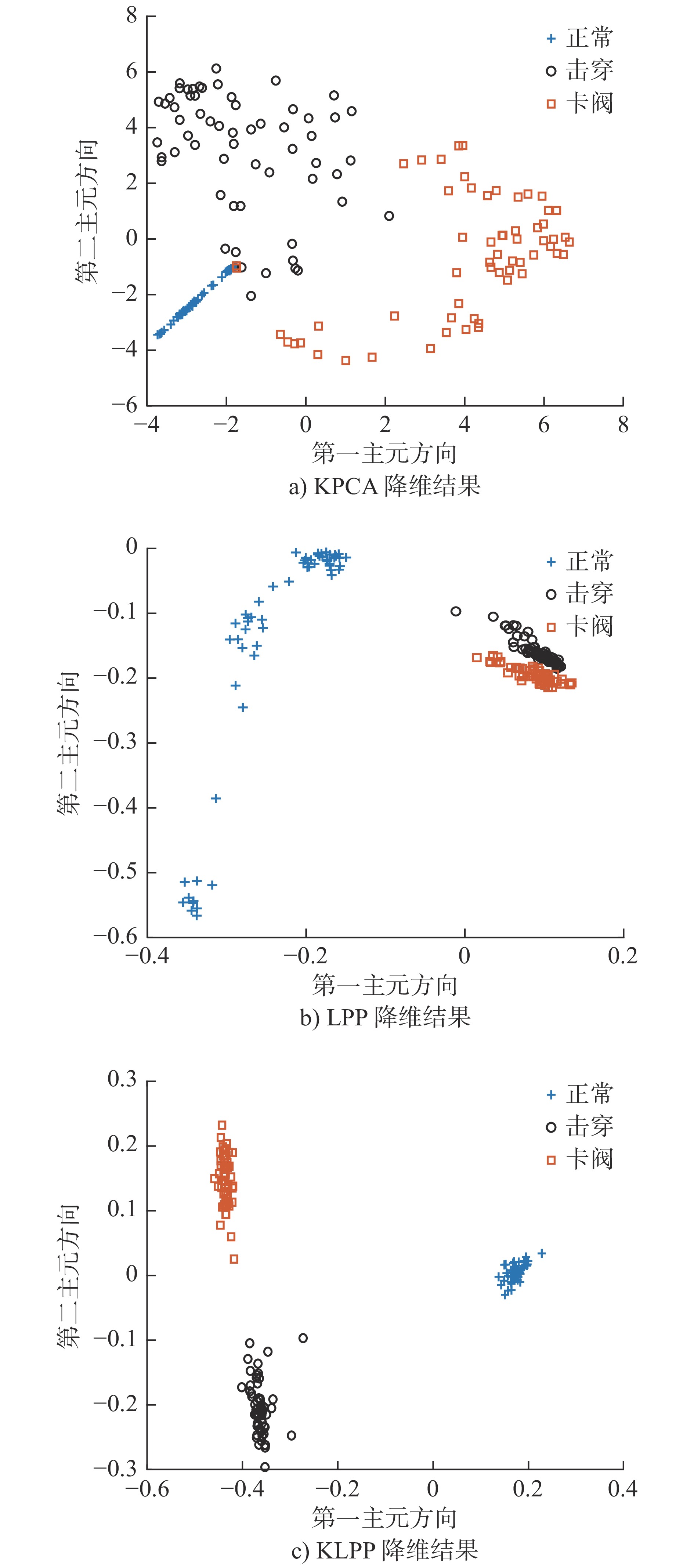
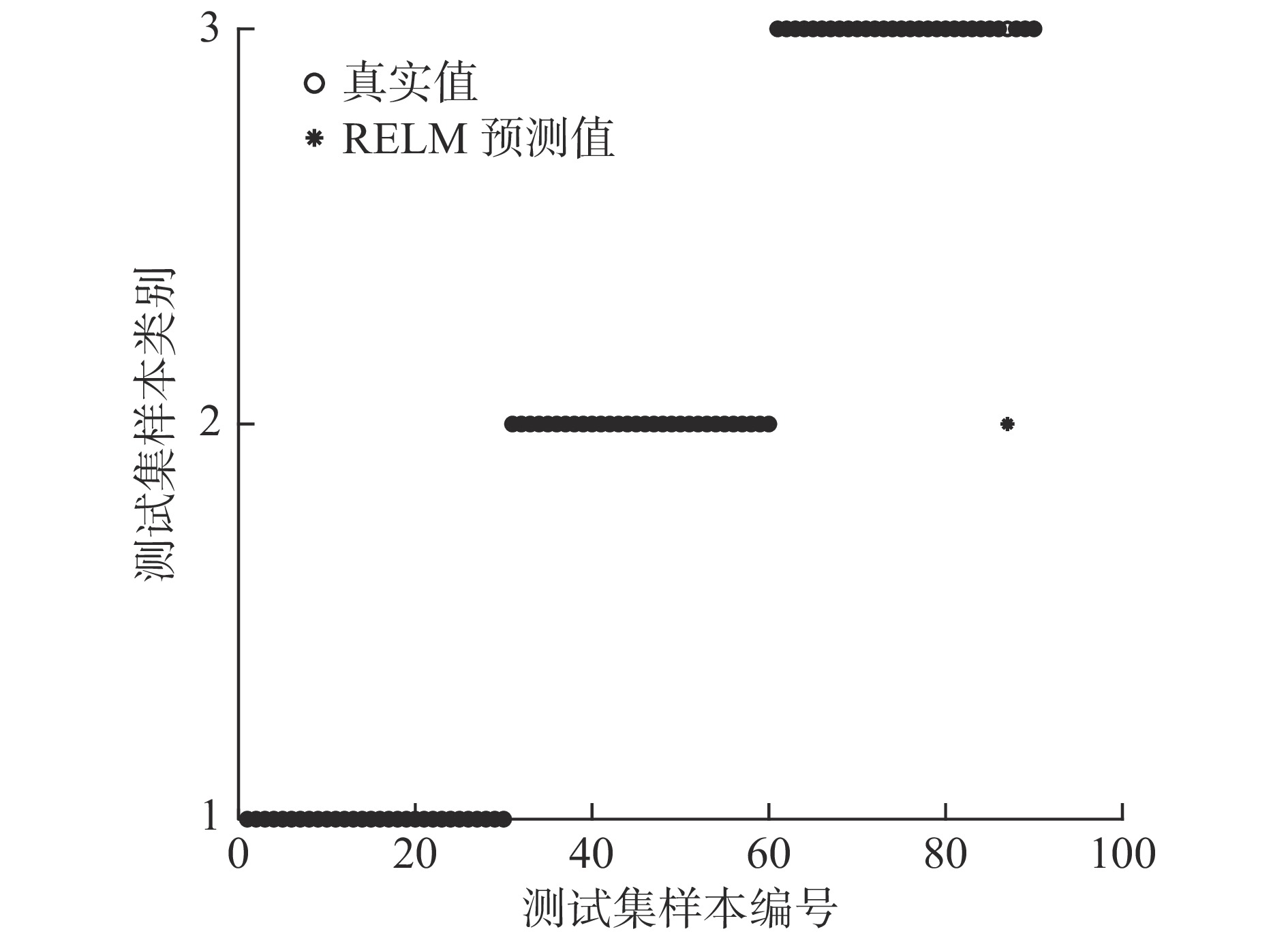
Check Valve Fault Diagnosis of High-pressure Diaphragm Pump with KLPP Feature Reduction and RELM
-
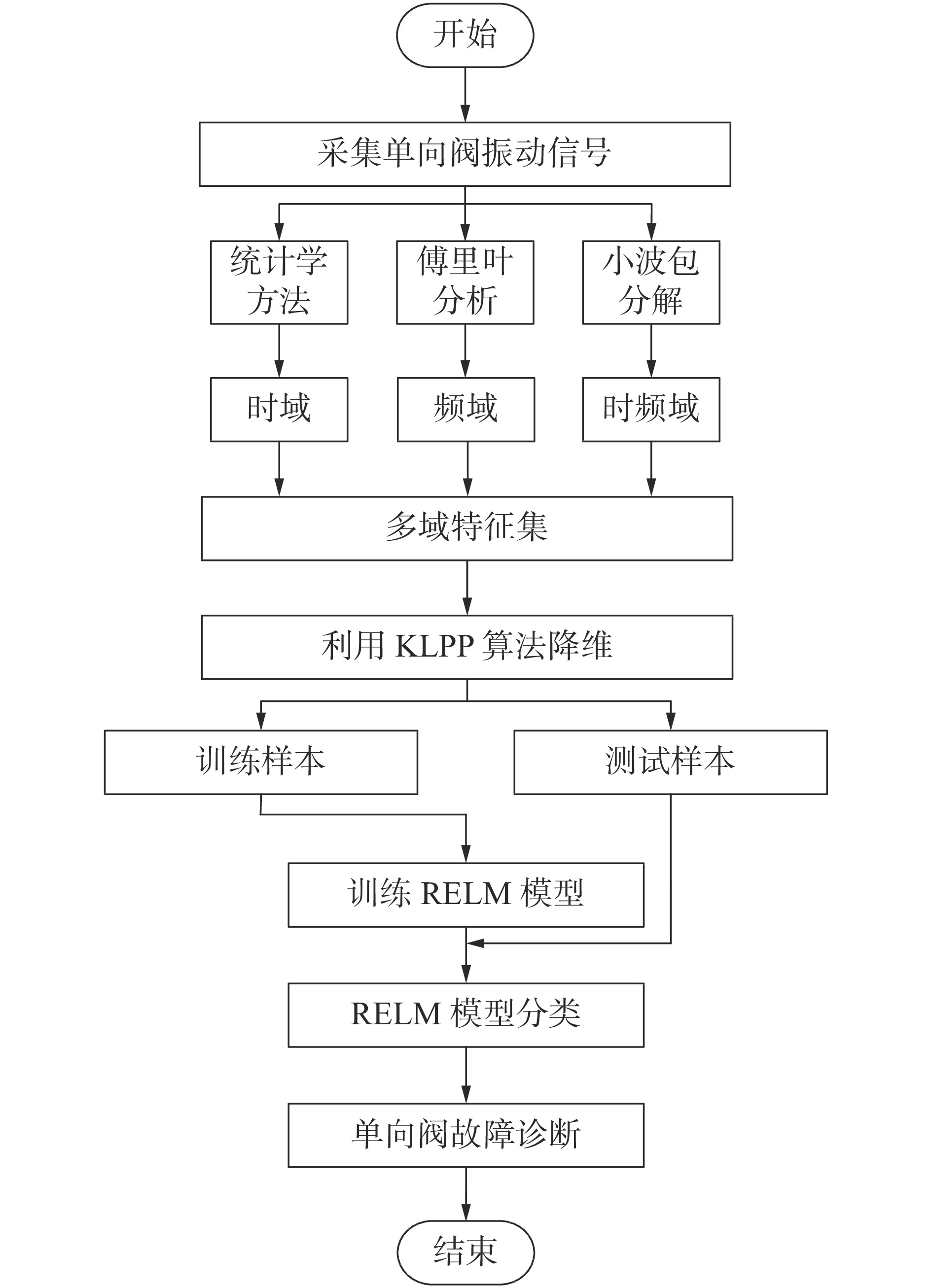
摘要: 为此提出基于核局部保持投影(KLPP)和正则化极限学习机(RELM)的高压隔膜泵单向阀故障诊断方法。首先,提取单向阀振动信号的时域、频域、时频域特征,构建多域特征集;然后,通过KLPP算法对构建的多域特征集进行维数约简;最后,建立基于RELM的故障诊断模型,用于识别单向阀运行状态。实验结果表明,基于多域特征的故障诊断方法检测精度高于单域特征识别方法;KLPP约简多域特征集,可以有效消除信息冗余;建立的RELM故障诊断模型识别精度达到98.89%,能够有效识别高压隔膜泵单向阀故障类型。Abstract: The single-domain feature cannot fully reflect the operating state of check valve of the high-pressure diaphragm pump, and the high-dimensional feature set composed of multi-domain features will produce dimensional disasters, and the information redundancy leads to low recognition accuracy of the fault diagnosis model. To this end, a fault diagnosis method for check valve of high-pressure diaphragm pump based on KLPP(Kernel local preservation projection) and RELM(Regularized extreme learning machine) is proposed in this paper. First, the time domain, frequency domain and time-frequency domain features of check valve vibration signal are respectively extracted to construct a multi-domain feature set. Then, dimensionality reduction is performed on the constructed multi-domain feature set through the KLPP algorithm. Finally, a fault diagnosis model based on RELM is established to identify the operating status of check valve. The experimental results show that the detection accuracy of the fault diagnosis method based on multi-domain features is higher than that of the single-domain feature recognition method; KLPP reduces the multi-domain feature set, which can effectively eliminate information redundancy; the established RELM fault diagnosis model has a recognition accuracy of 98.89%, which can effectively identify the fault type of check valve of the high-pressure diaphragm pump.
-
表 1 时域特征
Table 1. Time-domain features
特征参数 表达式 特征参数 表达式 特征参数 表达式 平均值 ${T_1} = \dfrac{1}{N}\displaystyle\sum\limits_{n = 1}^N {x(n)}$ 方差 ${T_7} = \dfrac{1}{N}\displaystyle\sum\limits_{n = 1}^N { { {\bigg( {x(n)} \bigg)}^2} }$ 脉冲指标 ${T_{13} } = \dfrac{ { {T_8} } }{ { {T_4} } }$ 标准差 ${T_2} = \sqrt {\dfrac{1}{ {N{{ - } }1} }\displaystyle\sum\limits_{n = 1}^N {\bigg[ {x(n) - {T_1} } \bigg]} }$ 最大值 $ {T_8} = \max \left| {x(n)} \right| $ 裕度指标 ${T_{14} } = \dfrac{ { {T_8} } }{ { {T_3} } }$ 方根幅值 ${T_{14} } = \dfrac{ { {T_8} } }{ { {T_3} } }$ 最小值 $ {T_9} = \min \left| {x(n)} \right| $ 偏度指标 ${T_{15} } = \dfrac{ { {T_5} } }{ { { {\bigg(\sqrt { {T_7} } \bigg)}^3} } }$ 绝对平均值 ${T_4} = \dfrac{1}{N}\displaystyle\sum\limits_{n = 1}^N {\left| {x(n)} \right|}$ 峰峰值 $ {T_{10}} = {T_8} - {T_9} $ 峭度指标 ${T_{16} } = \dfrac{ { {T_6} } }{ { { {\bigg(\sqrt { {T_7} } \bigg)}^2} } }$ 偏度 ${T_5} = \dfrac{1}{N}\displaystyle\sum\limits_{n = 1}^N { { {\bigg( {x(n)} \bigg)}^3} }$ 波形指标 ${T_{11} } = \dfrac{ { {T_2} } }{ { {T_4} } }$ 峭度 ${T_6} = \dfrac{1}{N}\displaystyle\sum\limits_{n = 1}^N { { {\bigg( {x(n)} \bigg)}^4} }$ 峰值指标 ${T_{12} } = \dfrac{ { {T_8} } }{ { {T_2} } }$ 表 2 频域特征
Table 2. frequency-domain features
特征参数 表达式 特征参数 表达式 特征参数 表达式 均值频率 ${F_1} = \dfrac{1}{K}\displaystyle\sum\limits_{k = 1}^K {s(k)}$ 频率特征6 ${F_6} = \sqrt {\dfrac{1}{K}\displaystyle\sum\limits_{k = 1}^K { { {\bigg({f_k} - {F_5}\bigg)}^2}s(k)} }$ 频率特征11 ${F_{11} } = \dfrac{ {\displaystyle\sum\limits_{k = 1}^K { { {\bigg({f_k} - {F_5}\bigg)}^3}s(k)} } }{ {K{ {({F_6})}^3} } }$ 频率中心 ${F_2} = \sqrt {\dfrac{1}{ {K - 1} }\displaystyle\sum\limits_{k = 1}^K { { {\bigg(s(k) - {F_1}\bigg)}^2} } }$ 频率特征7 ${F_7} = \sqrt {\dfrac{ {\displaystyle\sum\limits_{k = 1}^K {f_k^2s(k)} } }{ {\displaystyle\sum\limits_{k = 1}^K {s(k)} } } }$ 频率特征12 ${F_{12} } = \dfrac{ {\displaystyle\sum\limits_{k = 1}^K { { {\bigg({f_k} - {F_5}\bigg)}^4}s(k)} } }{ {K{ {({F_6})}^4} } }$ 标准差频率 ${F_3} = \dfrac{ {\displaystyle\sum\limits_{k = 1}^K { { {\bigg(s(k) - {F_1}\bigg)}^3} } } }{ {K{ {\bigg(\sqrt { {F_2} } \bigg)}^3} } }$ 频率特征8 ${F_8} = \sqrt {\dfrac{ {\displaystyle\sum\limits_{k = 1}^K {f_k^4s(k)} } }{ {\displaystyle\sum\limits_{k = 1}^K {f_k^2s(k)} } } }$ 频率特征13 ${F_{13} } = \dfrac{ {\displaystyle\sum\limits_{k = 1}^K {\sqrt {({f_k} - {F_5})s(k)} } } }{ {K{F_6} } }$ 频率特征4 ${F_4} = \dfrac{ {\displaystyle\sum\limits_{k = 1}^K { { {\bigg(s(k) - {F_1}\bigg)}^4} } } }{ {K{ {\bigg(\sqrt { {F_2} } \bigg)}^2} } }$ 频率特征9 ${F_9} = \dfrac{ {\displaystyle\sum\limits_{k = 1}^K {f_k^2s(k)} } }{ {\sqrt {\displaystyle\sum\limits_{k = 1}^K {s(k)} \displaystyle\sum\limits_{k = 1}^K {f_k^4s(k)} } } }$ 频率特征5 ${F_5} = \dfrac{ {\displaystyle\sum\limits_{k = 1}^K { {f_k}s(k)} } }{ {\displaystyle\sum\limits_{k = 1}^K {s(k)} } }$ 频率特征10 ${F_{10} } = \dfrac{ { {F_6} } }{ { {F_5} } }$ 表 3 单向阀3种状态多域特征样本
Table 3. Multi-domain features of the one-way valve in three states
状态 样本 特征值 正常 1 [0.1770,0.2189,0.3480,0.2633,0.0631,0.0765,2.8497,1.8592,−0.9904,0.1211,1.3216,5.3422,7.0607,8.4909,1.4981,5.2204,0.0086,0.0004,9.7908,146.7420,290.9450,28.3471,420.9275,843.8580,0.4988,0.0974,13.5441,412.3895,0.02404,0.8562,0.0930,0.0138,0.0172,0.0004,0.0025,0.0096,0.0070,0.1328,0.2209,0.0591,0.0699,0.0035,0.0152,0.0446,0.0347] 2 [0.1565,0.2278,0.3612,0.2728,0.0601,0.0893,3.2028,1.8960,−1.3068,0.1304,1.3239,5.2497,6.9500,8.3230,1.2767,5.2490,0.0097,0.0004,7.4746,94.6553,286.6772,27.6031,401.3355,798.7763,0.5024,0.0963,13.0351,408.7480,0.0261,0.7656,0.1220,0.0183,0.0767,0.0004,0.0014,0.0048,0.0108,0.2045,0.2567,0.0731,0.1970,0.0030,0.0089,0.0257,0.0489] 击穿 1 [0.0951,0.0870,0.1239,0.1016,0.0028,0.0006,0.4525,0.3423,−0.1102,0.0153,1.2197,2.7634,3.3704,3.9352,1.4512,2.3941,0.0017,0.0001,17.7957,375.2469,173.9553,10.6549,308.9678,850.6089,0.3632,0.0613,52.1945,4199.5463,0.0064,0.9667,0.0293,0.0010,0.0017,0.0001,0.0002,0.0008,0.0003,0.0328,0.1033,0.0069,0.0110,0.0009,0.0015,0.0058,0.0021] 2 [0.1143,0.1056,0.1387,0.1189,0.0036,0.0007,0.4575,0.3242,−0.1334,0.0192,1.1667,2.3369,2.7264,3.0707,1.3475,2.0194,0.0018,0.0001,19.6871,438.8704,183.7557,11.2595,321.8966,828.6363,0.3885,0.0613,45.3749,3345.3737,0.0068,0.9806,0.0141,0.0016,0.0020,0.0001,0.0002,0.0009,0.0005,0.0192,0.0600,0.0106,0.0122,0.0010,0.0017,0.0062,0.0039] 卡阀 1 [0.0845,0.0807,0.111,0.0927,0.0019,0.0004,0.4356,0.2849,−0.1507,0.0123,1.1973,2.5666,3.0731,3.5289,1.4025,2.3104,0.0020,0.0001,17.7270,379.3032,218.0078,11.2845,335,750.0681,0.4466,0.0518,35.1537,2433.5674,0.0073,0.8993,0.0779,0.0072,0.0081,0,0.0002,0.0060,0.0013,0.0955,0.1988,0.0357,0.0391,0.0004,0.0014,0.0307, 0.0086] 2 [0.0923,0.0915,0.1204,0.1030,0.0023,0.0005,0.4654,0.3179,−0.1475,0.0145,1.1686,2.6408,3.0861,3.4725,1.3412,2.1462,0.0020,0.0001,17.7732,379.7815,199.1707,11.2900,323.3263,781.6425,0.4136,0.05670,39.9310,2848.9510,0.0072,0.9427,0.0429,0.0039,0.0059,0,0.0001,0.0032,0.0013,0.0556,0.1351,0.0215,0.0301,0.0004,0.0012,0.0183,0.0085] 表 4 单域和多域特征RELM故障诊断结果
Table 4. RELM fault diagnosis results using single-domain and multi-domain features
特征提取方法 故障识别精度/% 正常 击穿 卡阀 平均 时域 83.33 83.33 66.67 77.78 频域 80 86.67 73.33 80 时频域 80 70 63.33 71.11 多域 90 90 76.67 85.56 表 5 多域特征降维后故障诊断结果
Table 5. Fault diagnosis results after dimensionality reduction of multi-domain features
方法 故障识别精度/% 正常 击穿 卡阀 平均 KPCA-ELM 93.33 90 83.33 88.89 KPCA-RELM 93.33 93.33 83.33 90 LPP-ELM 96.67 93.33 90 93.33 LPP-RELM 96.67 96.67 90 94.44 KLPP-ELM 100 96.67 93.33 96.67 KLPP-RELM 100 100 96.67 98.89 -
[1] 潘震, 黄国勇, 吴漫. 基于参数优化VMD和增强多尺度排列熵的单向阀故障诊断[J]. 振动与冲击, 2020, 39(15): 118-125.PAN Z, HUANG G Y, WU M. Check valve fault diagnosis based on VMD parametric optimization and enhanced multi-scale permutation entropy[J]. Journal of Vibration and Shock, 2020, 39(15): 118-125. (in Chinese) [2] 牟竹青, 黄国勇, 吴建德, 等. 基于DEMD的高压隔膜泵单向阀早期故障诊断[J]. 振动、测试与诊断, 2018, 38(4): 758-764.MOU Z Q, HUANG G Y, WU J D, et al. Early fault diagnosis of high pressure diaphragm pump check valve based on differential empirical mode decomposition[J]. Journal of Vibration, Measurement & Diagnosis, 2018, 38(4): 758-764. (in Chinese) [3] ZHOU C J, MA J, WU J D, et al. An adaptive VMD method based on improved Goa to extract early fault feature of rolling bearings[J]. International Journal of Innovative Computing, Information and Control, 2019, 15(4): 1485-1505. [4] SUN C, YIN H P, LI Y X, et al. A novel rolling bearing vibration impulsive signals detection approach based on dictionary learning[J]. IEEE/CAA Journal of Automatica Sinica, 2021, 8(6): 1188-1198. doi: 10.1109/JAS.2020.1003438 [5] 励文艳, 程珩, 赵立红, 等. 基于局部s变换和极限学习机的柱塞泵滑靴磨损故障诊断[J]. 液压与气动, 2019(12): 15-21. doi: 10.11832/j.issn.1000-4858.2019.12.002LI W Y, CHENG H, ZHAO L H, et al. Shoe wear fault diagnosis of axial piston pump based on local s transform and extreme learning machine[J]. Chinese Hydraulics & Pneumatics, 2019(12): 15-21. (in Chinese) doi: 10.11832/j.issn.1000-4858.2019.12.002 [6] 孙岩, 彭高亮. 改进胶囊网络的滚动轴承故障诊断方法[J]. 哈尔滨工业大学学报, 2021, 53(1): 23-28. doi: 10.11918/202004163SUN Y, PENG G L. Improved capsule network method for rolling bearing fault diagnosis[J]. Journal of Harbin Institute of Technology, 2021, 53(1): 23-28. (in Chinese) doi: 10.11918/202004163 [7] WANG L, JIANG S L, ZHANG Q, et al. Multi-domain high-resolution platform for integrated spectroscopy and microscopy characterizations[J]. Chinese Journal of Chemical Physics, 2020, 33(6): 680-685. doi: 10.1063/1674-0068/cjcp2006093 [8] 石明宽, 赵荣珍. 基于局部边缘判别投影的机械故障诊断方法[J]. 振动、测试与诊断, 2021, 41(1): 126-132. doi: 10.16450/j.cnki.issn.1004-6801.2021.01.018SHI M K, ZHAO R Z. A method of mechanical fault diagnosis based on locality margin discriminant projection[J]. Journal of Vibration, Measurement & Diagnosis, 2021, 41(1): 126-132. (in Chinese) doi: 10.16450/j.cnki.issn.1004-6801.2021.01.018 [9] 施莹, 庄哲, 林建辉. 基于卷积稀疏表示及等距映射的轴承故障诊断[J]. 振动、测试与诊断, 2019, 39(5): 1081-1088.SHI Y, ZHUANG Z, LIN J H. Fault diagnosis of bearing based on CSR-ISOMAP[J]. Journal of Vibration, Measurement & Diagnosis, 2019, 39(5): 1081-1088. (in Chinese) [10] 张成, 郭青秀, 冯立伟, 等. 基于局部保持投影−加权k近邻规则的多模态间歇过程故障检测策略[J]. 控制理论与应用, 2019, 36(10): 1682-1689. doi: 10.7641/CTA.2019.80858ZHANG C, GUO Q X, FENG L W, et al. Fault detection strategy based on locality preserving projections-weighted k nearest neighbors in multimodal batch processes[J]. Control Theory & Applications, 2019, 36(10): 1682-1689. (in Chinese) doi: 10.7641/CTA.2019.80858 [11] 刘长良, 曹威, 王梓齐. 基于MMI-PCA-KLPP二次降维和模糊树模型的NOx浓度软测量方法[J]. 华北电力大学学报, 2020, 47(1): 79-86.LIU C L, CAO W, WANG Z Q. Soft measurement method of NOx concentration based on MMI-PCA-KLPP and fuzzy tree model[J]. Journal of North China Electric Power University, 2020, 47(1): 79-86. (in Chinese) [12] DONG L K, CHEN S Y, MOU M L, et al. The effect of resonant magnetic perturbation with different poloidal mode numbers on peeling–ballooning modes[J]. Plasma Science and Technology, 2020, 22(11): 115101. doi: 10.1088/2058-6272/aba3bd [13] ABUASSBA A O M, ZHANG Y, LUO X, et al. A heterogeneous ensemble of extreme learning machines with correntropy and negative correlation[J]. Tsinghua Science and Technology, 2017, 22(6): 691-701. doi: 10.23919/TST.2017.8195351 [14] YAN X A, JIA M P. A novel optimized SVM classification algorithm with multi-domain feature and its application to fault diagnosis of rolling bearing[J]. Neurocomputing, 2018, 313: 47-64. doi: 10.1016/j.neucom.2018.05.002 [15] GUO J, HE J X. Dynamic response analysis of ship-bridge collisions experiment[J]. Journal of Zhejiang University-SCIENCE A, 2020, 21(7): 525-534. doi: 10.1631/jzus.A1900382 [16] ZHANG Y X, YOU D Y, GAO X D, et al. Online monitoring of welding status based on a DBN model during laser welding[J]. Engineering, 2019, 5(4): 671-678. doi: 10.1016/j.eng.2019.01.016 [17] 王海云, 王剑平, 罗付华. 融合多层次特征Faster R-CNN的金属板带材表面缺陷检测研究[J]. 机械科学与技术, 2021, 40(2): 262-269.WANG H Y, WANG J P, LUO F H. Study on surface defect detection of metal sheet and strip using faster R-CNN with multilevel feature[J]. Mechanical Science and Technology for Aerospace Engineering, 2021, 40(2): 262-269. (in Chinese) [18] 潘超, 陈祥, 蔡国伟, 等. 基于小波包尺度-能量占比的变压器三相不平衡绕组振动特征辨识[J]. 仪器仪表学报, 2020, 41(4): 129-137. doi: 10.19650/j.cnki.cjsi.J2005982PAN C, CHEN X, CAI G W, et al. Identification of winding vibration characteristics of three-phase unbalanced transformer based on scale-energy ratio of wavelet packet[J]. Chinese Journal of Scientific Instrument, 2020, 41(4): 129-137. (in Chinese) doi: 10.19650/j.cnki.cjsi.J2005982 [19] ZHENG S S, FU Y L, LAI K K, et al. An improvement to multiple criteria ABC inventory classification using Shannon entropy[J]. Journal of Systems Science and Complexity, 2017, 30(4): 857-865. doi: 10.1007/s11424-017-5061-8 [20] 何冬, 黄国勇, 钱恩丽, 等. 基于总变差降噪与RQA的单向阀故障诊断[J]. 电子测量与仪器学报, 2021, 35(2): 65-72. doi: 10.13382/j.jemi.B2003372HE D, HUANG G Y, QIAN E L, et al. Check valve fault diagnosis based on total variation de-nosing and recurrence quantification analysis[J]. Journal of Electronic Measurement and Instrumentation, 2021, 35(2): 65-72. (in Chinese) doi: 10.13382/j.jemi.B2003372 -






 下载:
下载: