Effect of Calculation Method for Asperity Distribution on Contact Solution
-
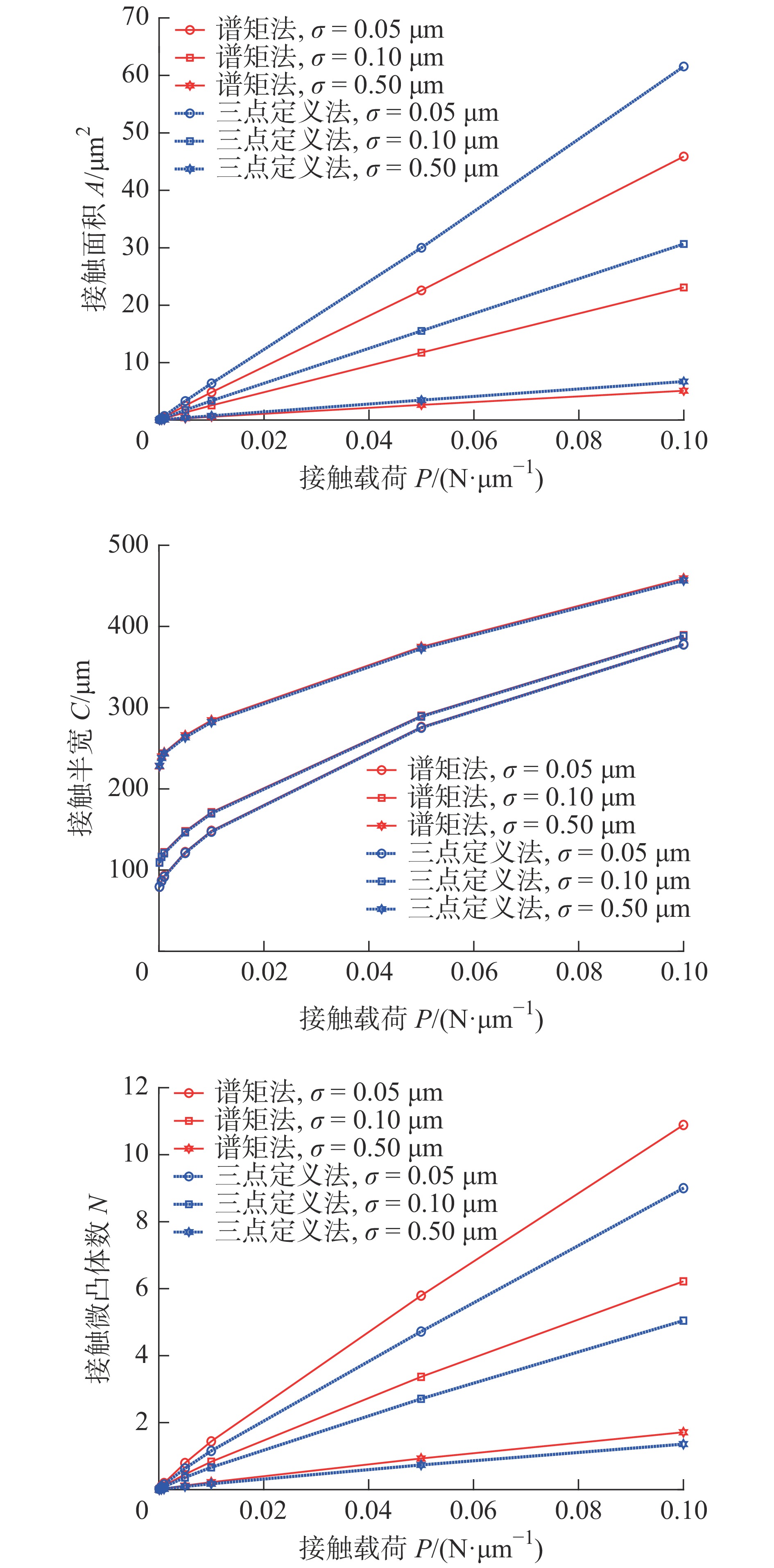
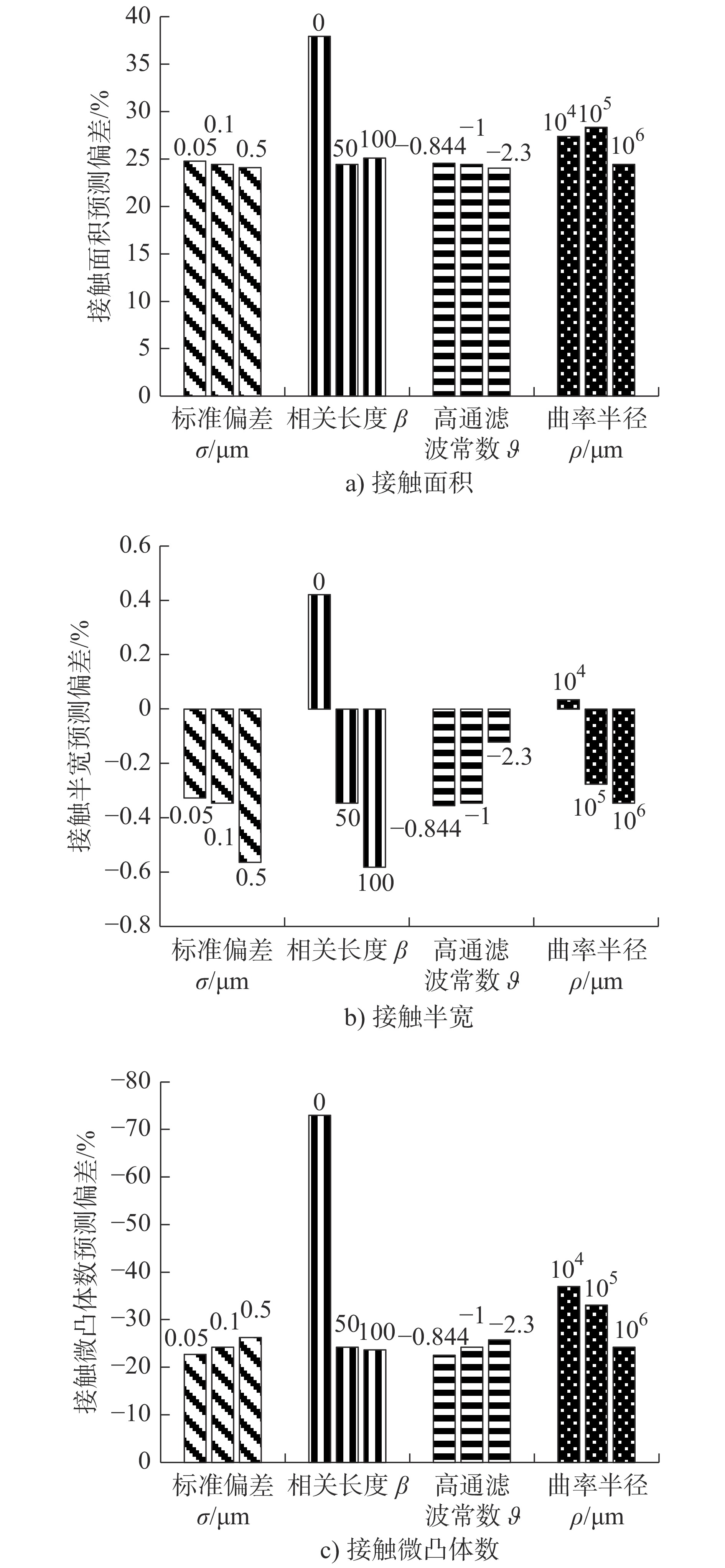
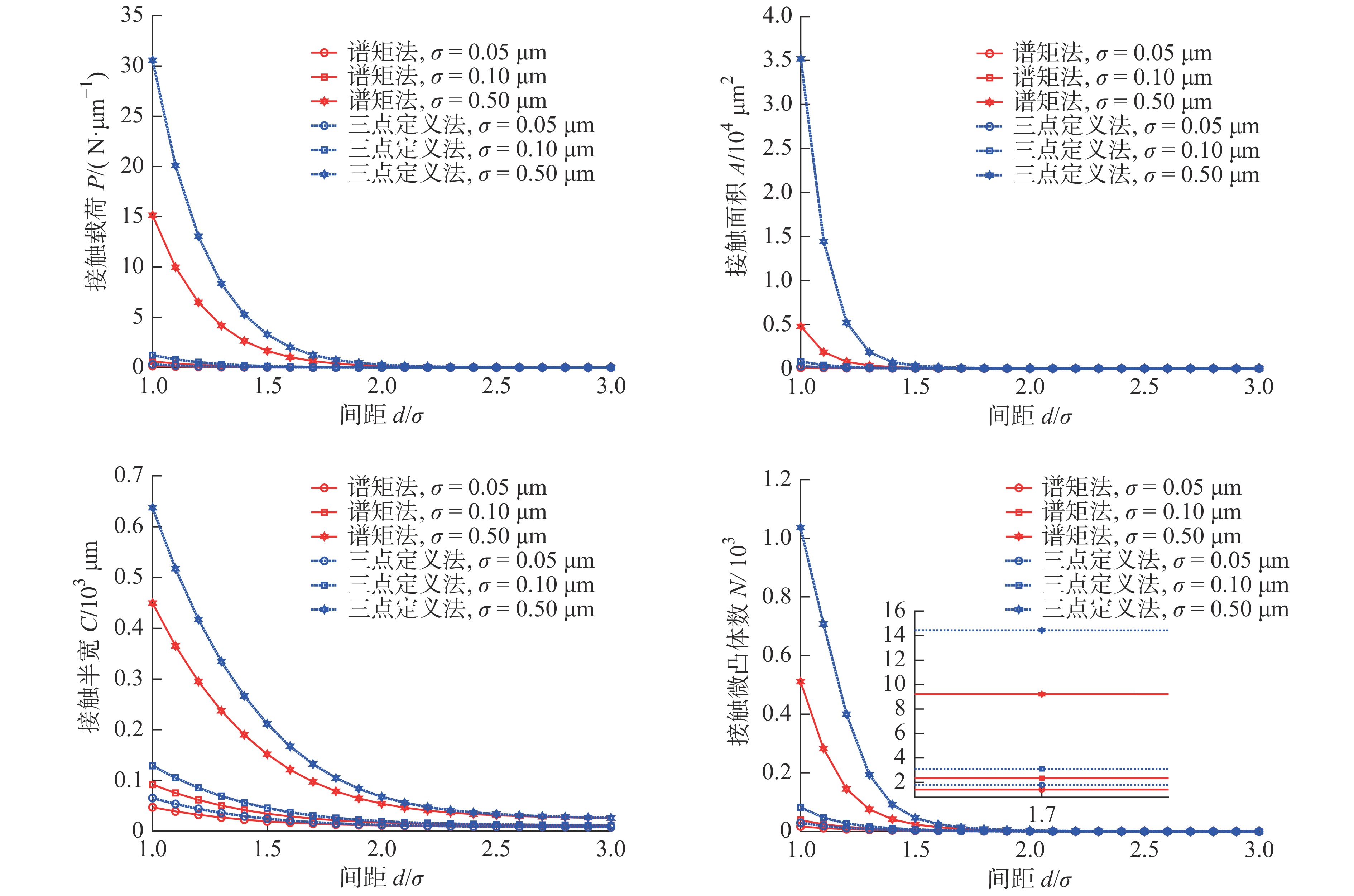
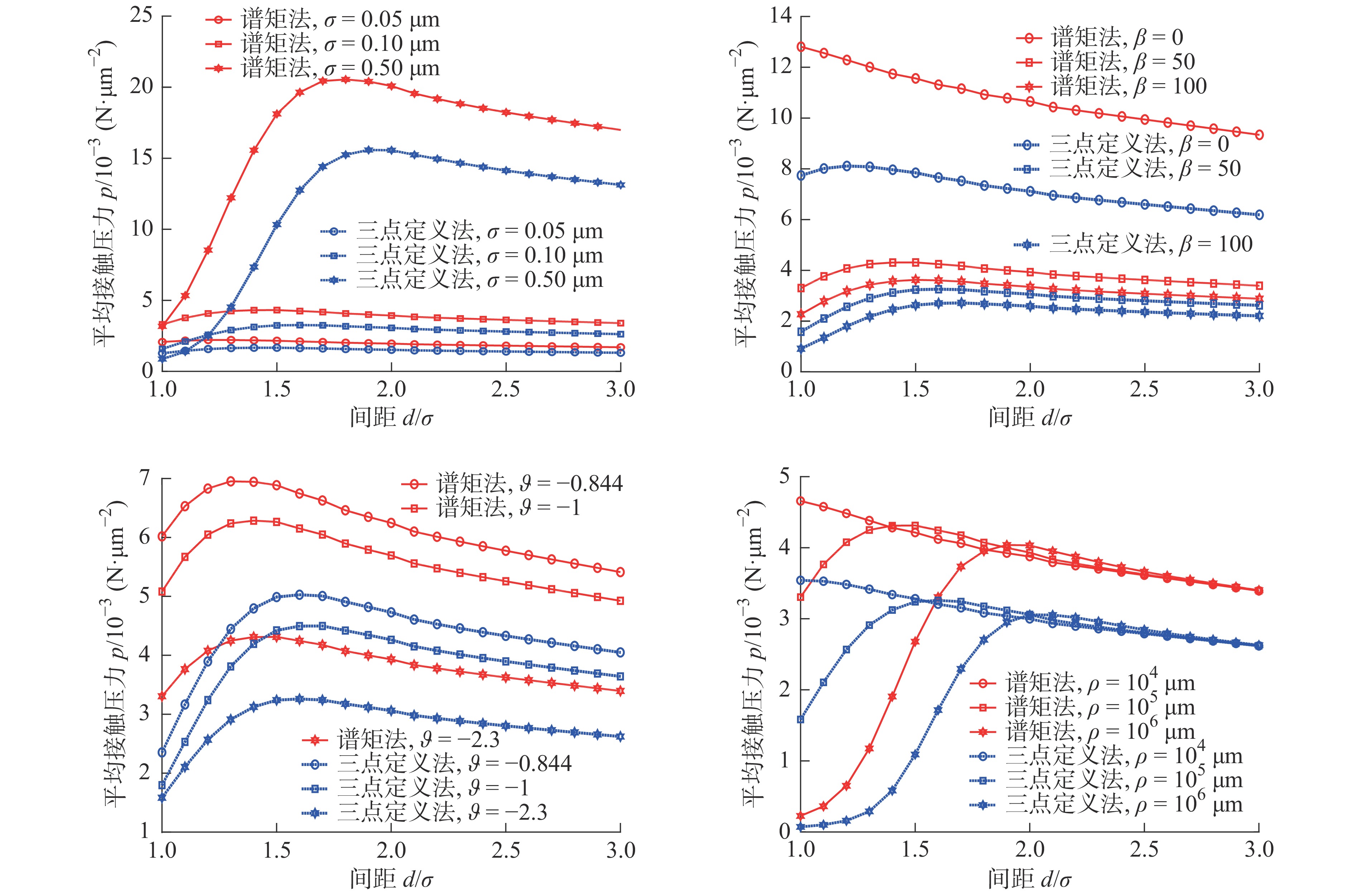
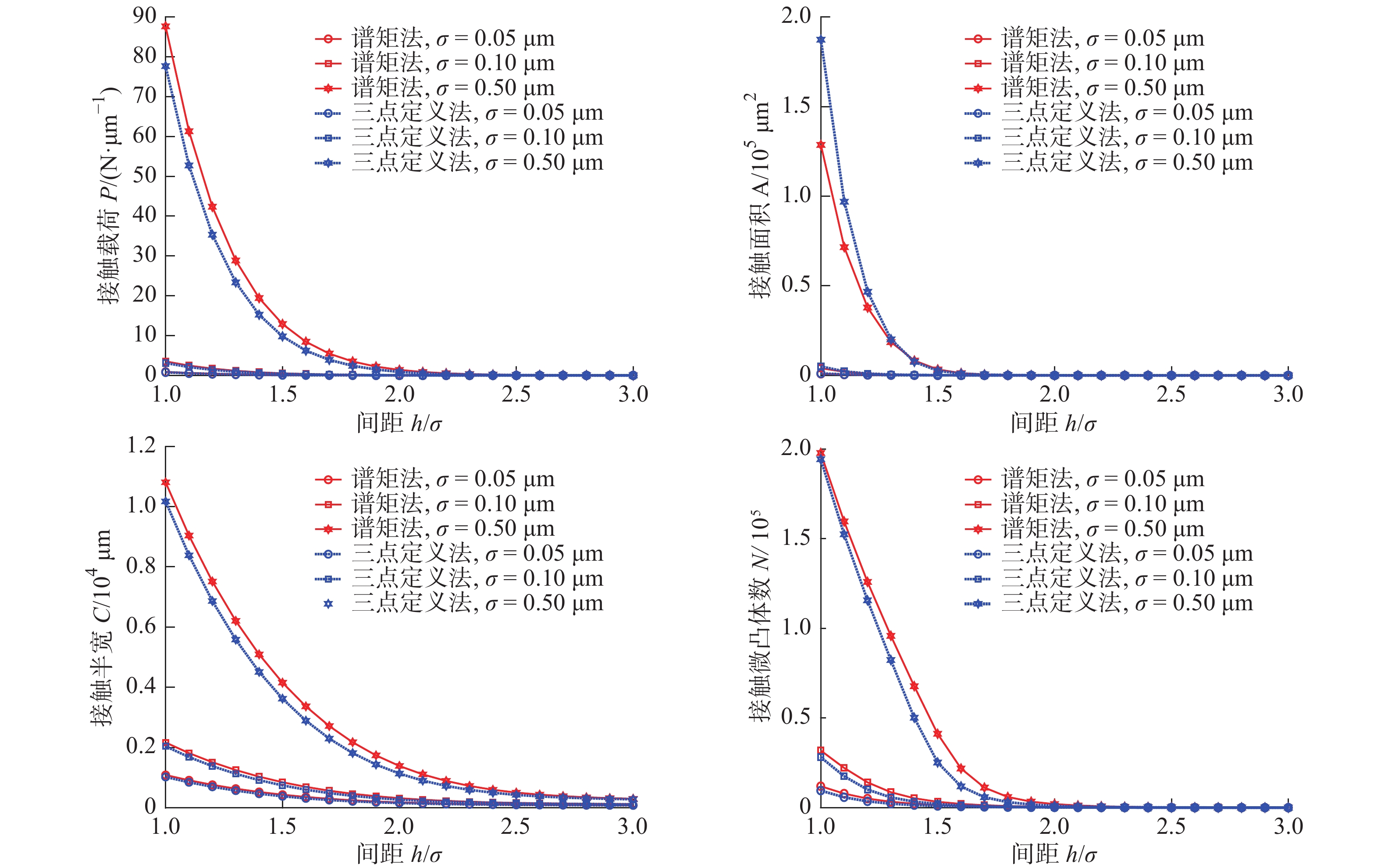
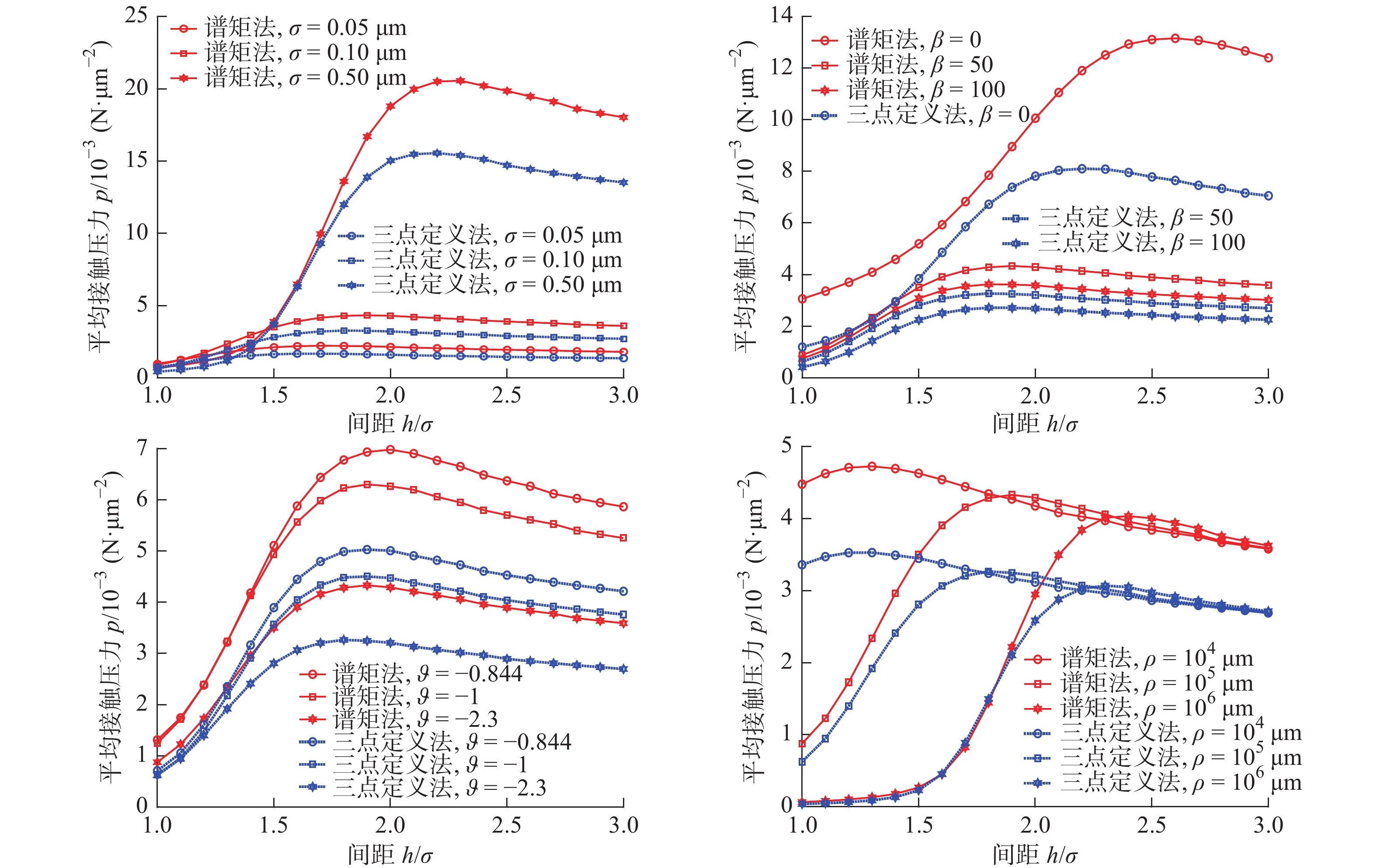
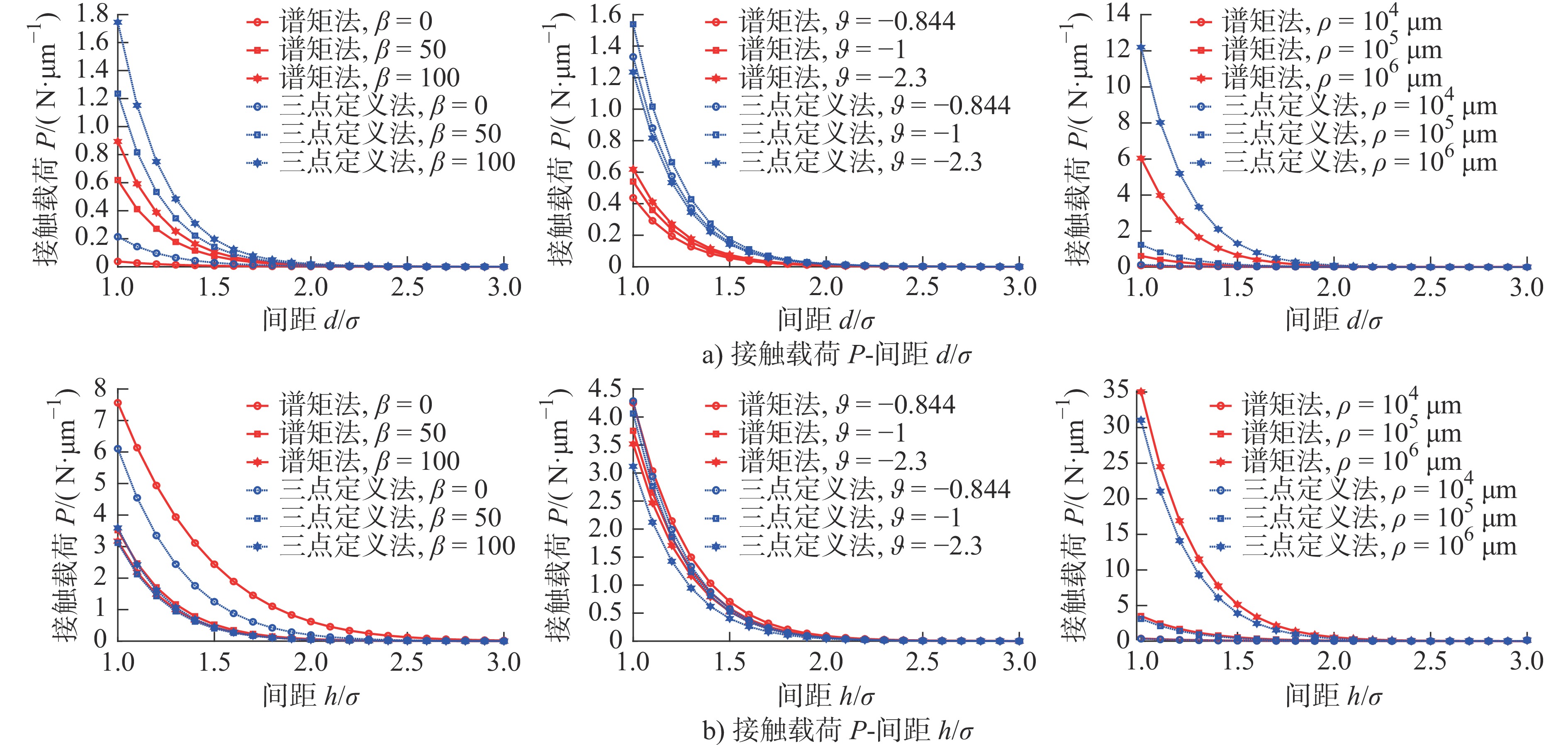
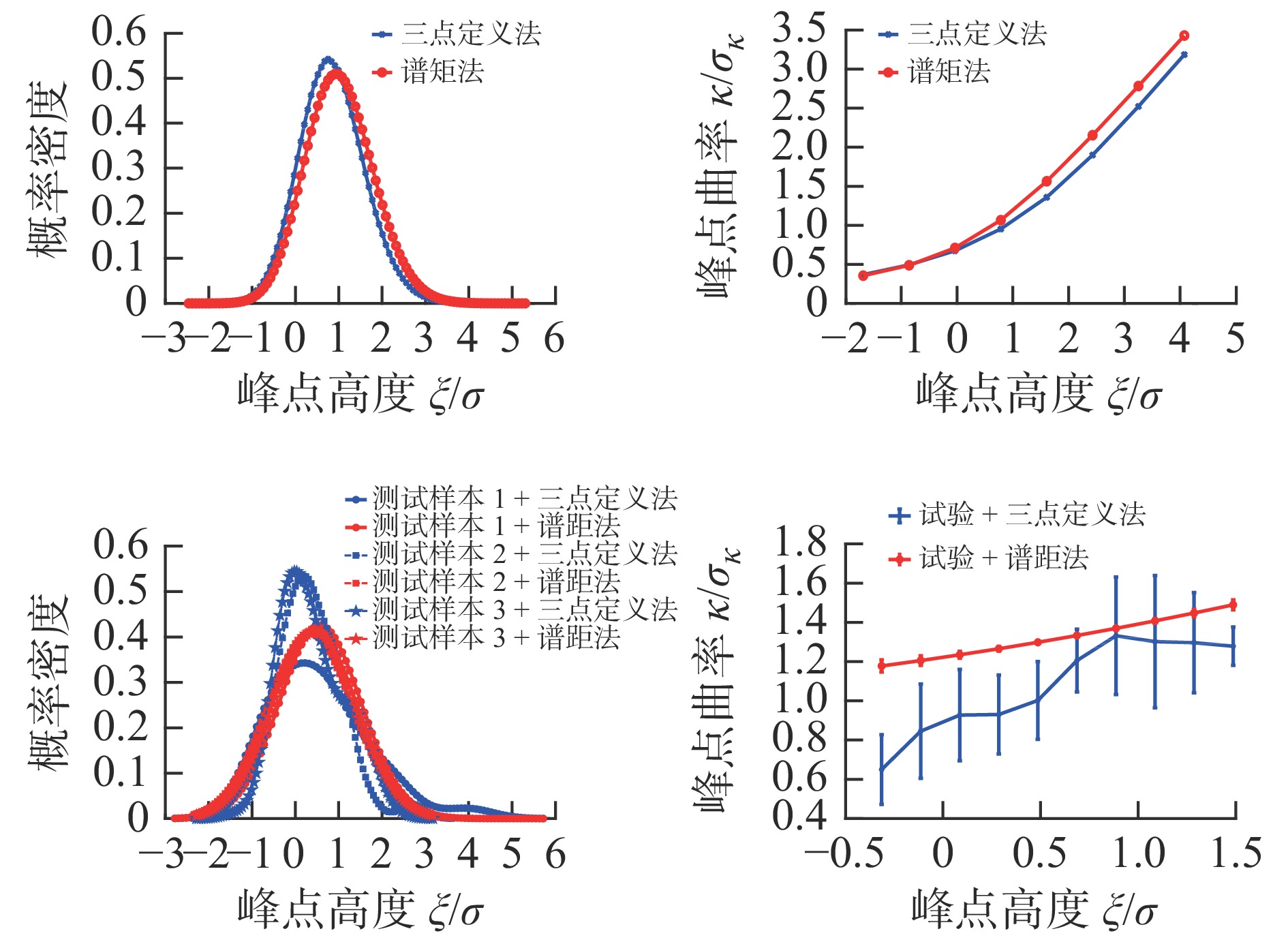
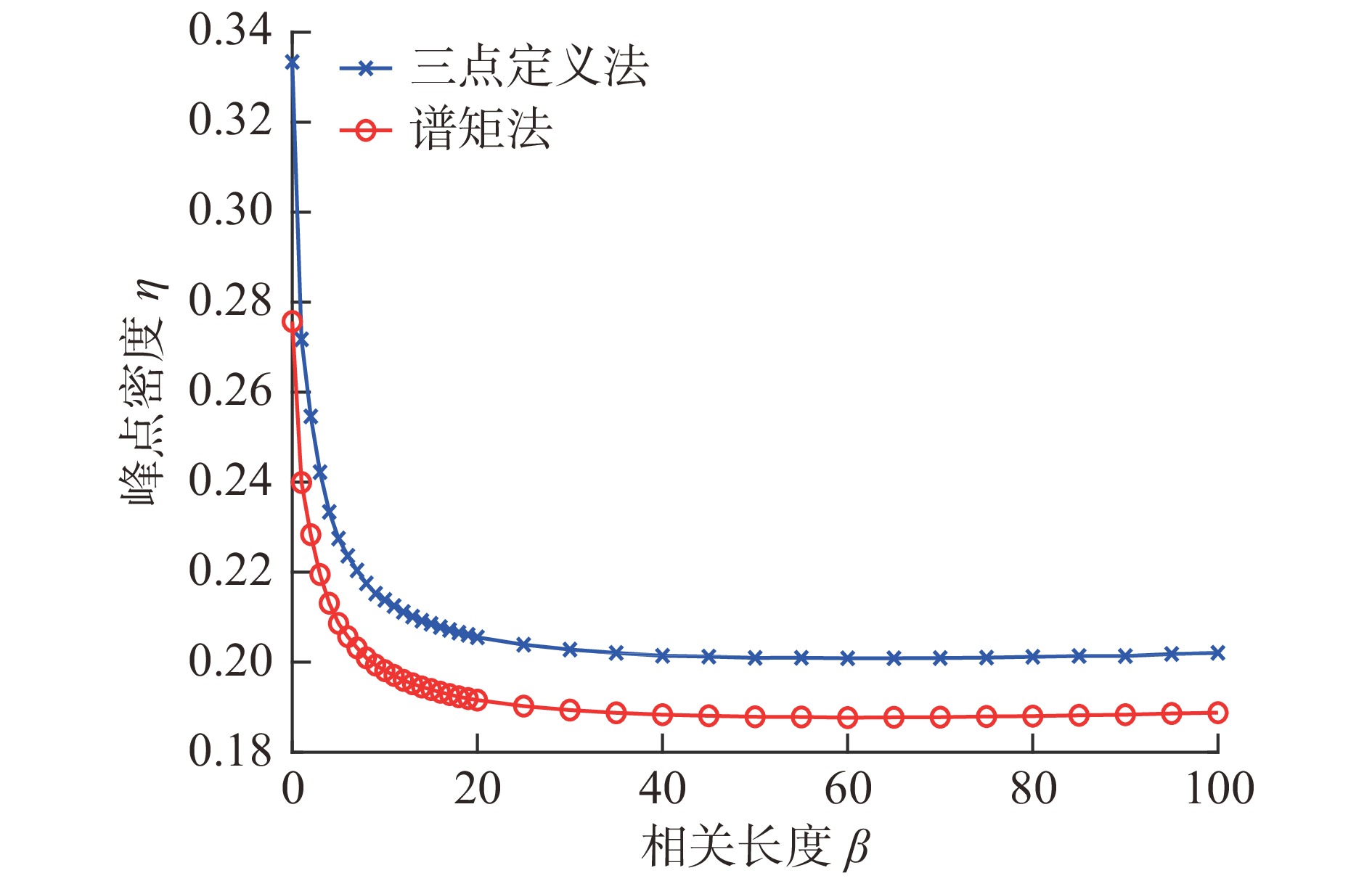
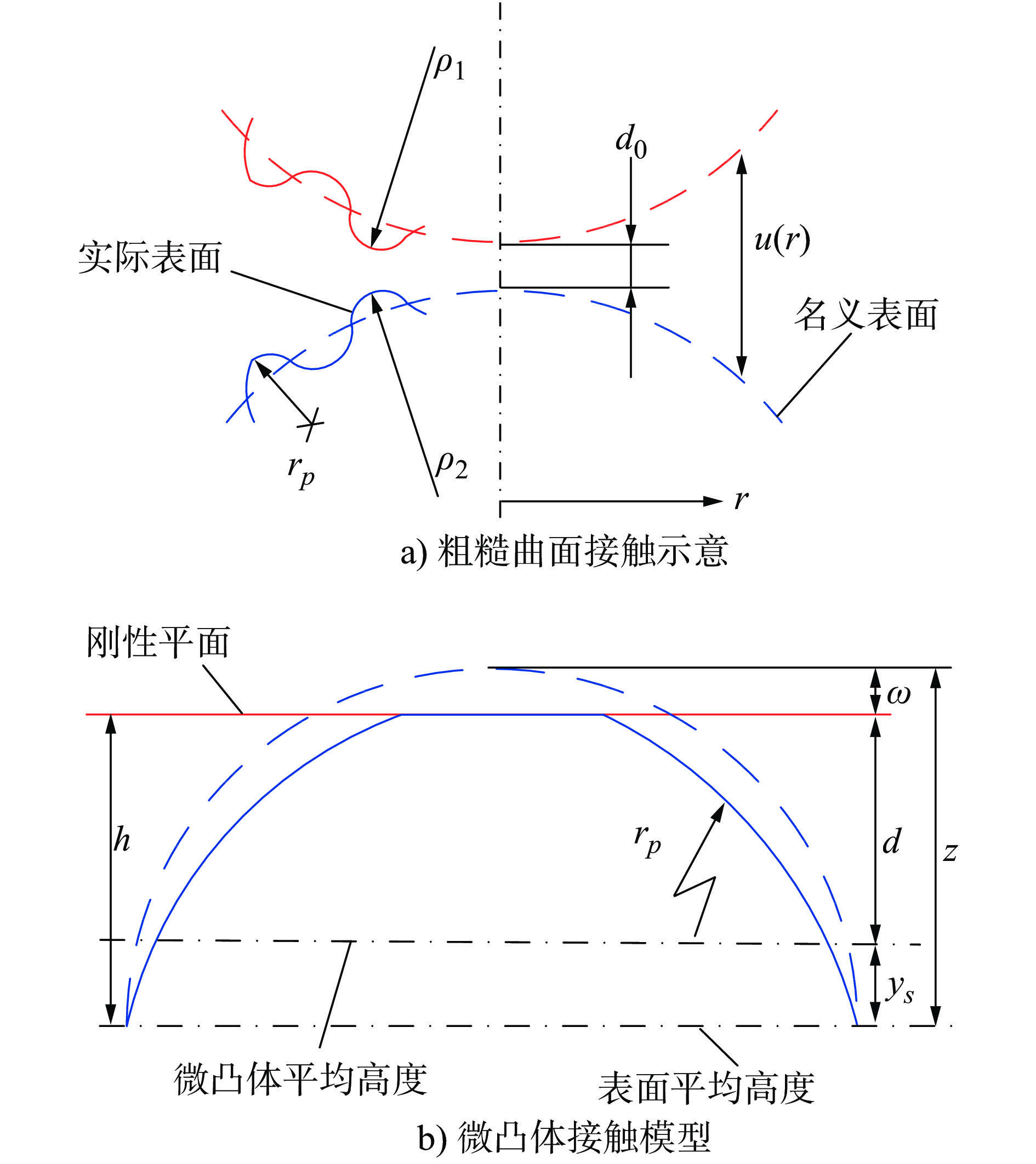
摘要: 为借助Greenwood-Williamson(GW)接触模型开展粗糙表面接触分析,基于微凸体识别的参数定义法和基于随机过程理论的谱矩法都被广泛用于微凸体分布参数计算。为厘清应用不同计算方法产生的接触求解差异,针对粗糙曲面接触,利用快速傅里叶变换重构获得不同统计分布下的粗糙表面随机样本,由三点定义法和谱矩法分别计算仿真样本的微凸体峰点分布参数,对样本开展GW接触分析,得到两种计算方法下接触预测结果,对结果进行了对比讨论,分析了样本表面统计分布参数、高通滤波常数、曲率半径和载荷的影响。最后,通过试验数据对谱矩法的计算偏差进行了检验,对微凸体分布参数计算给出了建议。Abstract: To perform contact analysis of rough surface with Greenwood-Williamson (GW) model, both the asperity identification scheme based method and spectral moment approach on the basis of random process theory are widely used for the calculation of asperity distribution parameters. In order to clarify the difference in contact solution caused by the application of the two methods, rough surface samples with various statistical distributions are randomly generated by using Fast Fourier Transformation. Asperity peak distribution parameters of the simulated samples are determined by using three-point definition and spectral moment approach, respectively. Contact analysis of the samples are carried out by using GW model with the two methods. The calculated results are compared and the effects of the statistical distribution parameters, high pass filtering, radius of curvature and load are discussed. Finally, the experimental data are used to inspect the deviation of spectral moment approach. Suggestions for calculating the asperity distribution parameters are provided.
-
Key words:
- rough surface /
- contact /
- asperity /
- spectral moment approach /
- GW model
-
表 1 接触面积预测相对偏差
Table 1. Relative deviation in predicted contact area
σ/μm P/(N·μm−1) 0.0001 0.001 0 0.010 0 0.100 0 0.05 23.15% 24.40% 24.36% 25.46% 0.10 23.60% 23.86% 24.31% 24.70% 0.50 23.81% 23.46% 23.80% 23.97% -
[1] THOMAS T R. Rough surfaces[M]. 2nd ed. London: Imperial College Press, 1999: 133-147 [2] WEN Y Q, TANG J Y, ZHOU W, et al. An improved simplified model of rough surface profile[J]. Tribology International, 2018, 125: 75-84. doi: 10.1016/j.triboint.2018.04.025 [3] GREENWOOD J A, WILLIAMSON J B P. Contact of nominally flat surfaces[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1966, 295(1442): 300-319. [4] GREENWOOD J A, WU J J. Surface roughness and contact: an apology[J]. Meccanica, 2001, 36(6): 617-630. doi: 10.1023/A:1016340601964 [5] SISTA B, VEMAGANTI K. Estimation of statistical parameters of rough surfaces suitable for developing micro-asperity friction models[J]. Wear, 2014, 316(1-2): 6-18. doi: 10.1016/j.wear.2014.04.012 [6] 运睿德, 丁北. 考虑多尺度接触状态的新接触模型[J]. 机械工程学报, 2019, 55(9): 80-89. doi: 10.3901/JME.2019.09.080YUN R D, DING B. New fractal contact model considered multi-scale levels[J]. Journal of Mechanical Engineering, 2019, 55(9): 80-89. (in Chinese) doi: 10.3901/JME.2019.09.080 [7] WHITEHOUSE D J. The digital measurement of peak parameters on surface profiles[J]. Journal of Mechanical Engineering Science, 1978, 20(4): 221-227. doi: 10.1243/JMES_JOUR_1978_020_037_02 [8] WEN Y Q, TANG J Y, ZHOU W, et al. A reconstruction and contact analysis method of three-dimensional rough surface based on ellipsoidal asperity[J]. Journal of Tribology, 2020, 142(4): 041502. doi: 10.1115/1.4045633 [9] 朱少禹, 孙军, 李彪, 等. 粗糙表面湍流润滑的随机模型[J]. 机械工程学报, 2019, 55(9): 71-79. doi: 10.3901/JME.2019.09.071ZHU S Y, SUN J, LI B, et al. Stochastic models for turbulent lubrication of rough surfaces[J]. Journal of Mechanical Engineering, 2019, 55(9): 71-79. (in Chinese) doi: 10.3901/JME.2019.09.071 [10] WEN Y Q, TANG J Y, ZHOU W, et al. A new elliptical microcontact model considering elastoplastic deformation[J]. Proceedings of the Institution of Mechanical Engineers, Part J:Journal of Engineering Tribology, 2018, 232(11): 1352-1364. doi: 10.1177/1350650117753447 [11] ZHAO Y W, CHANG L. A model of asperity interactions in elastic-plastic contact of rough surfaces[J]. Journal of Tribology, 2001, 123(4): 857-864. doi: 10.1115/1.1338482 [12] 韩姣皎, 杜飞, 徐超. 粗糙界面法向接触理论模型与实验结果对比研究[J]. 机械科学与技术, 2018, 37(12): 1875-1882. doi: 10.13433/j.cnki.1003-8728.20180091HAN J J, DU F, XU C. Comparative study on analytical models and experimental results for normal contact of rough surfaces[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(12): 1875-1882. (in Chinese) doi: 10.13433/j.cnki.1003-8728.20180091 [13] JOHNSONK L. 接触力学[M]. 徐秉业, 罗学富, 刘信声, 等译. 北京: 高等教育出版社, 1992: 451-481JOHNSON K L. Contact mechanics[M]. XU B Y, LUO X F, LIU X S, et al, trans. Beijing: Higher Education Press, 1992: 451-481. (in Chinese) [14] NAYAK P R. Random process model of rough surfaces[J]. Journal of Lubrication Technology, 1971, 93(3): 398-407. doi: 10.1115/1.3451608 [15] McCool J I. Comparison of models for the contact of rough surfaces[J]. Wear, 1986, 107(1): 37-60. doi: 10.1016/0043-1648(86)90045-1 [16] POGAČNIK A, KALIN M. How to determine the number of asperity peaks, their radii and their heights for engineering surfaces: a critical appraisal[J]. Wear, 2013, 300(1-2): 143-154. doi: 10.1016/j.wear.2013.01.105 [17] KALIN M, POGAČNIK A, ETSION I, et al. Comparing surface topography parameters of rough surfaces obtained with spectral moments and deterministic methods[J]. Tribology International, 2016, 93: 137-141. doi: 10.1016/j.triboint.2015.09.013 [18] ZHOU W, TANG J Y, HE Y F. Formulae of roughness peak distribution parameters with standard deviation and correlation length[J]. Proceedings of the Institution of Mechanical Engineers, Part J:Journal of Engineering Tribology, 2015, 229(12): 1395-1408. doi: 10.1177/1350650115579212 [19] PAWAR G, PAWLUS P, ETSION I, et al. The effect of determining topography parameters on analyzing elastic contact between isotropic rough surfaces[J]. Journal of Tribology, 2013, 135(1): 011401. doi: 10.1115/1.4007760 [20] LO C C. Elastic contact of rough cylinders[J]. International Journal of Mechanical Sciences, 1969, 11(1): 105-115. doi: 10.1016/0020-7403(69)90083-6 -







 下载:
下载: