Improved VMD-ITD Joint Denoising Method for Rock Fracture Acoustic Emission Signals
-
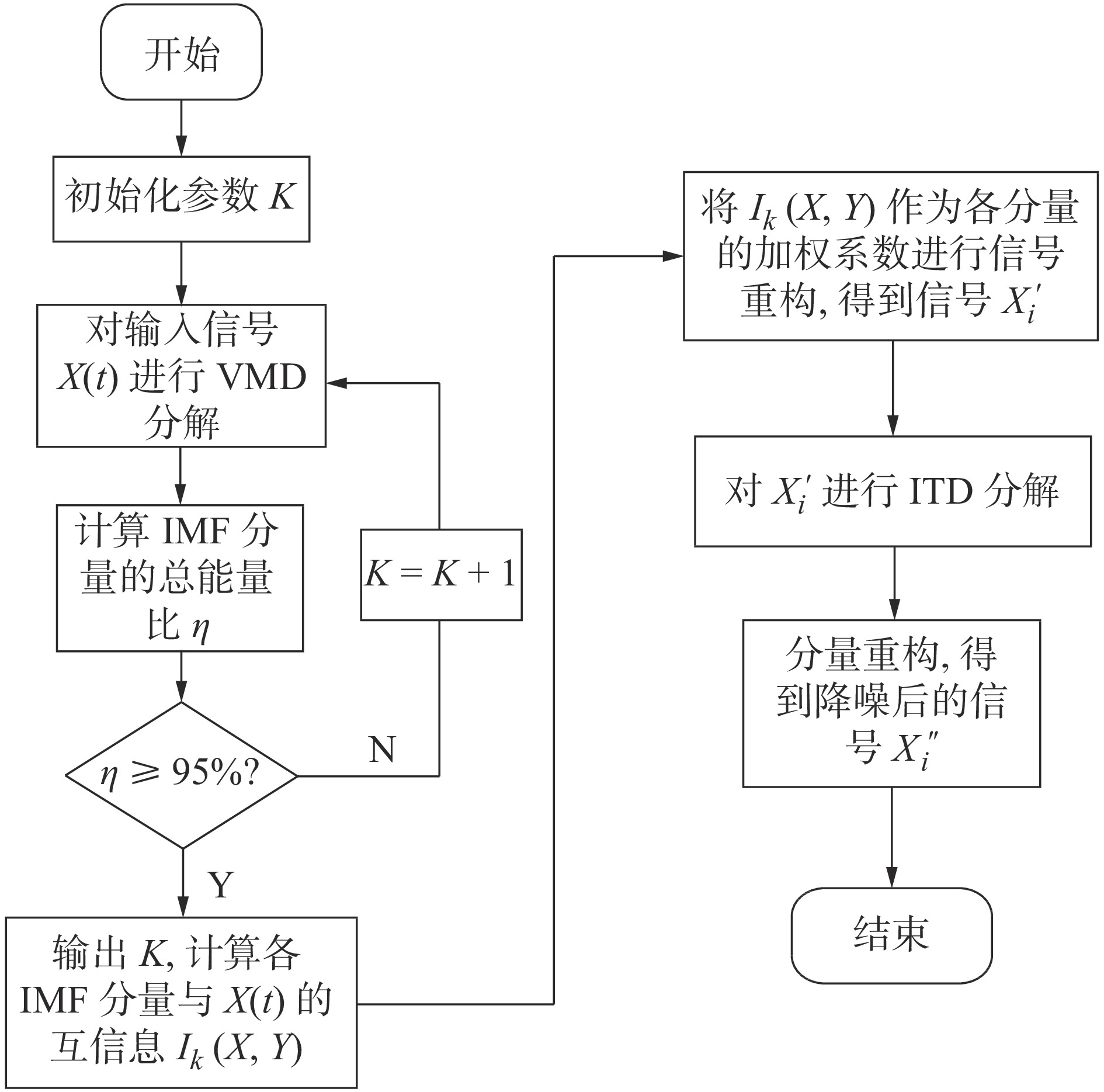
摘要: 针对岩石破裂声发射信号具有非线性、非平稳以及大样本的特点和传统VMD、ITD算法对降噪处理时存在一定局限性的问题,提出一种改进VMD-ITD联合降噪方法。以钨岩为研究对象,首先采用分量能量比作为VMD的终止条件,将岩石破裂声发射信号分解得到多个IMF分量,将各分量与原始信号的互信息量作为各分量的加权因子进行重构信号,再对重构信号进行ITD分解以达到二次降噪的目的,最后以均方根误差与信噪比为去噪效果评价指标,对比分析VMD、ITD以及改进VMD-ITD联合降噪算法降噪效果。通过试验验证,改进VMD-ITD联合降噪算法在抑制非平稳信号噪声中,其均方根误差为4.552 1,信噪比为10.012 8。相比单一的VMD、ITD算法,降噪效果更好。Abstract: Aiming at the characteristics of non-linear, non-stationary and large sample of rock fracture acoustic emission signals and the problem that traditional VMD and ITD algorithms have some limitations in denoising, an improved VMD-ITD joint denoising method is proposed. Taking tungsten rock as the research object, firstly, the component energy ratio is used as the termination condition of VMD, and rock fracture acoustic emission signal is decomposed into multiple IMF components. The mutual information between each component and original signal is used as the weighting factor of each component to reconstruct the signal, and then reconstructed signal is decomposed by ITD to achieve the purpose of secondary noise reduction. Finally, taking root mean square error and signal-to-noise ratio as the evaluation indexes,denoising effects of VMD, ITD and improved VMD-ITD joint denoising algorithm are compared and analyzed. Experiments show that improved VMD-ITD joint denoising algorithm has a root mean square error of 4.552 1 and a signal-to-noise ratio of 10.012 8. Compared with single VMD and ITD algorithms, it is better.
-
Key words:
- rock fractureacoustic emission signal /
- joint denoising /
- VMD /
- ITD /
- mutual information
-
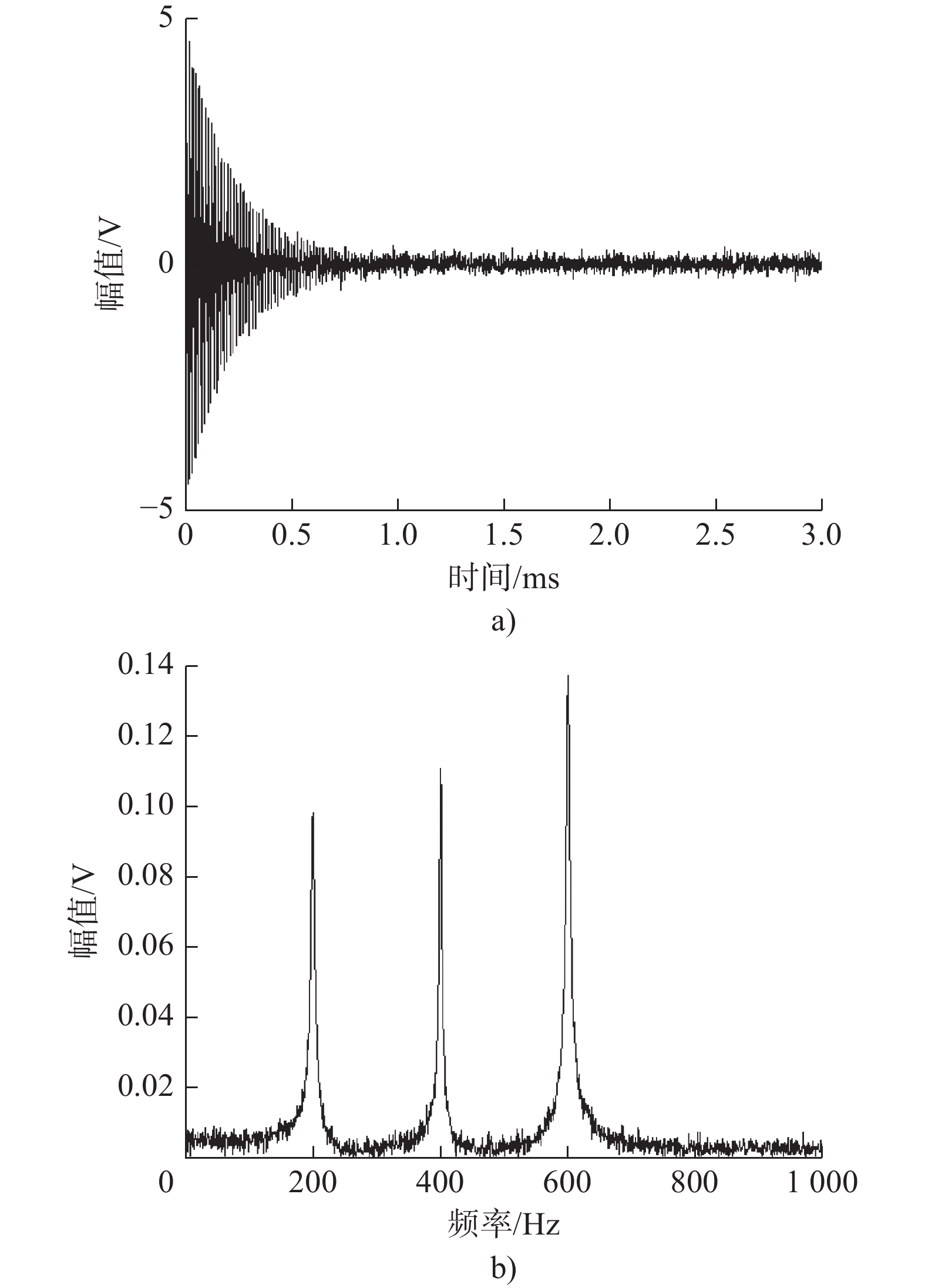
表 1 各IMF与加噪仿真信号的互信息量
Table 1. Mutual Information between each IMF and the simulated noisy signal
IMF序号 互信息量 IMF序号 互信息量 1 0.068 6 0.179 2 0.426 7 0.055 3 0.415 8 0.048 4 0.363 9 0.035 5 0.591 10 0.026 表 2 3种算法降噪后信号的信噪比与均方根误差
Table 2. Signal-to-noise ratio (SNR) and root mean square error (RMSE) of the denoised signals using three algorithms
降噪算法 均方根误差 信噪比 VMD 1.1534 6.8562 ITD 0.9003 10.2032 (IP)VMD-ITD 0.1586 14.2877 表 3 传感器SR150M的基本参数
Table 3. Basic parameters of the sensors
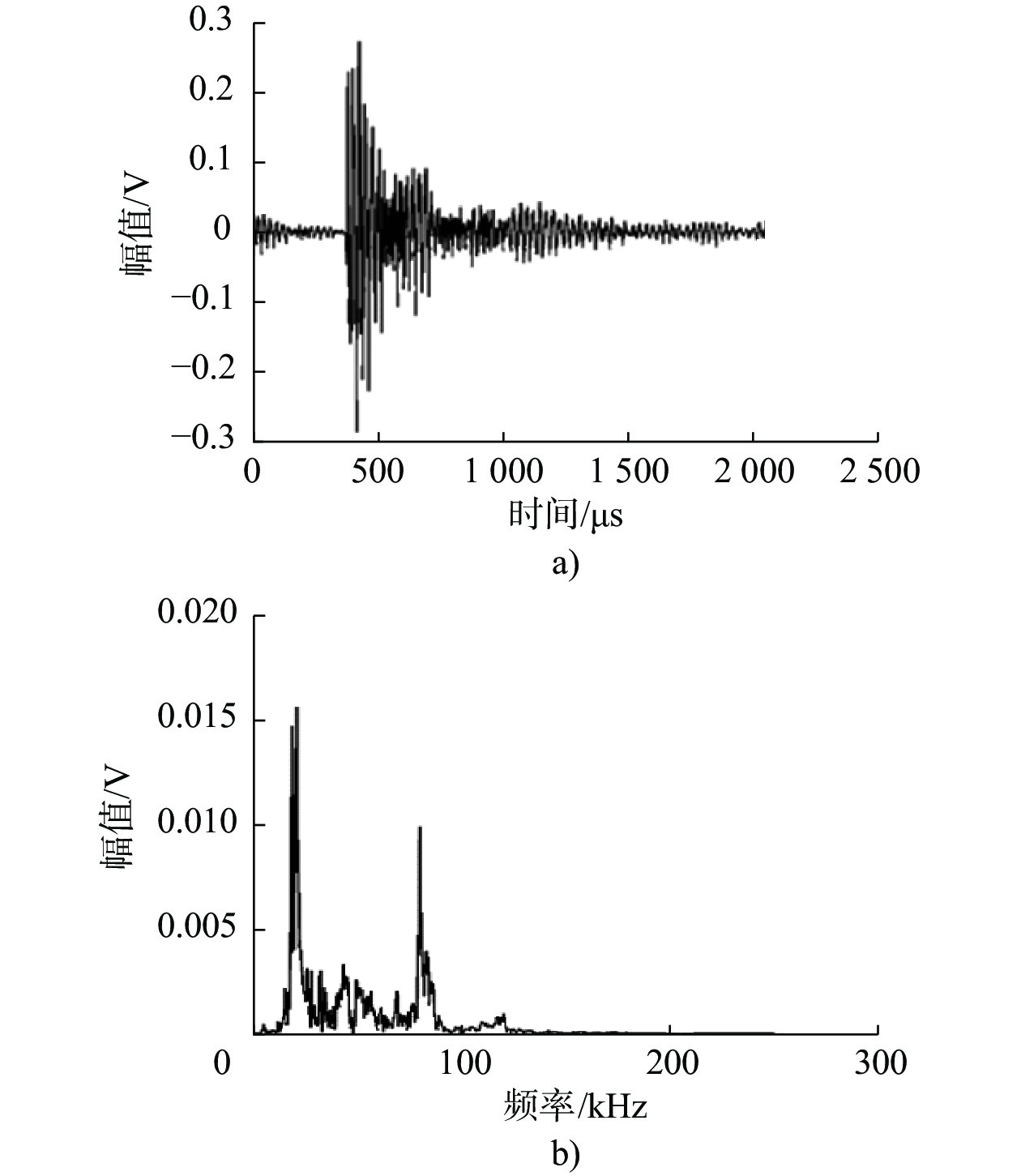
接收面材料 频率范围/kHz 谐振频率/kHz 灵敏度峰值/dB 陶瓷 60 ~ 400 150 >75 表 4 各IMF与含噪原始信号的互信息量
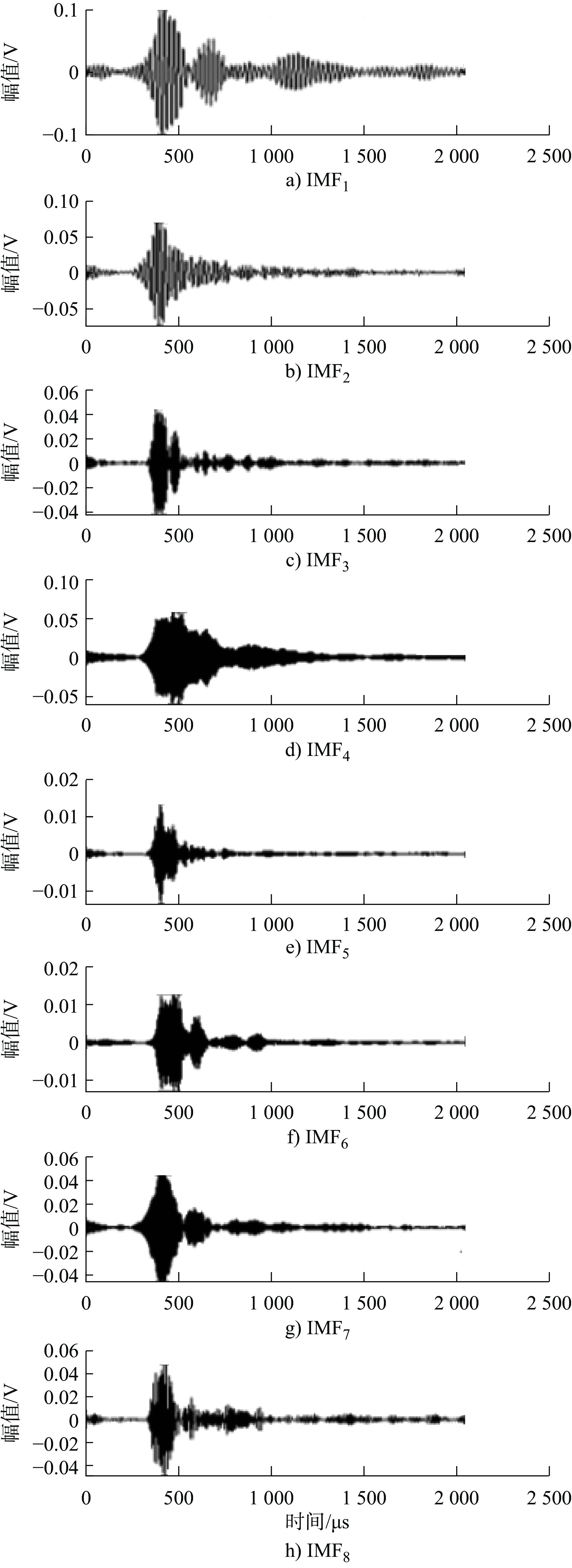
Table 4. Mutual information between each IMF and the noise-containing original signal
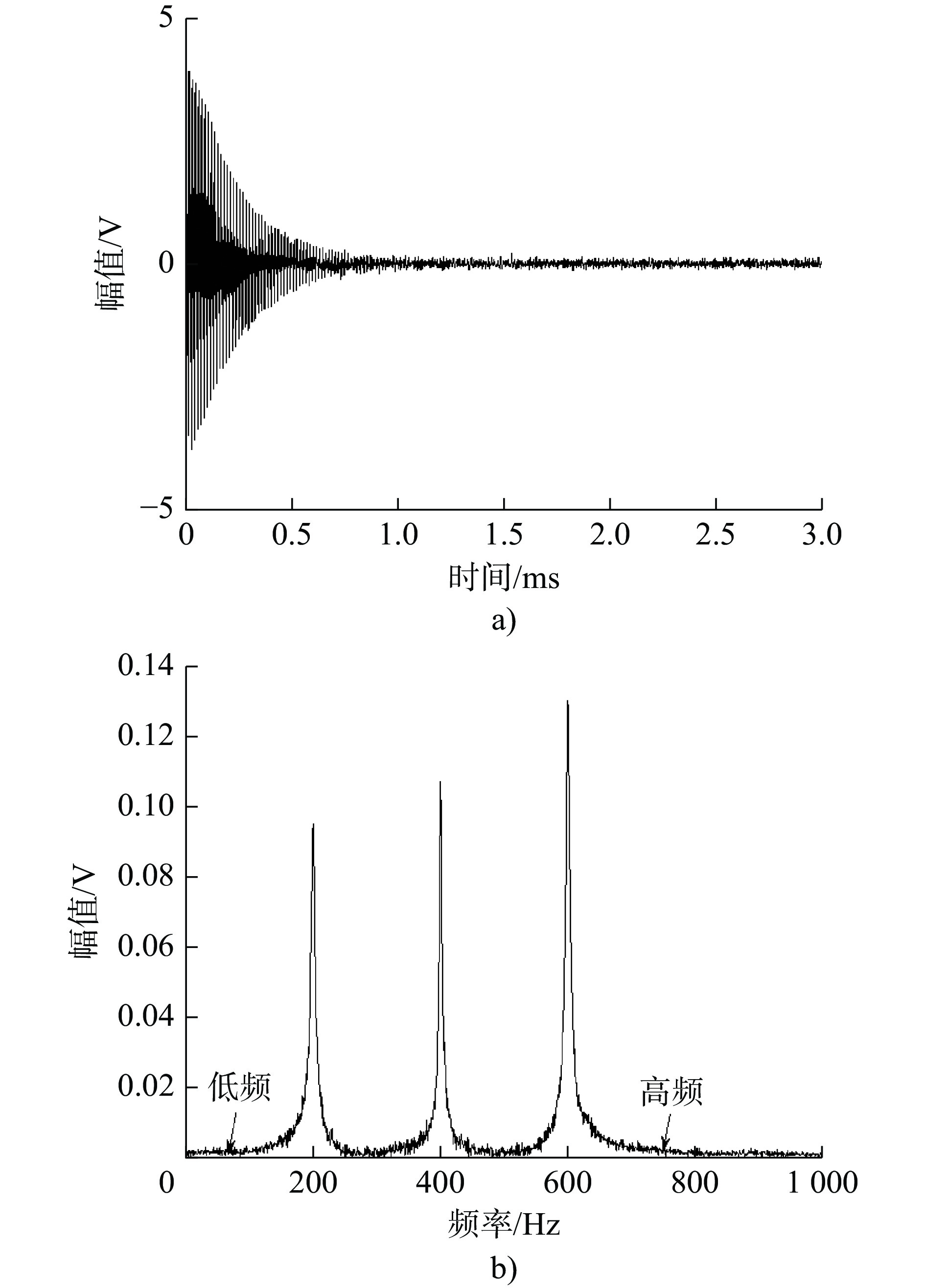
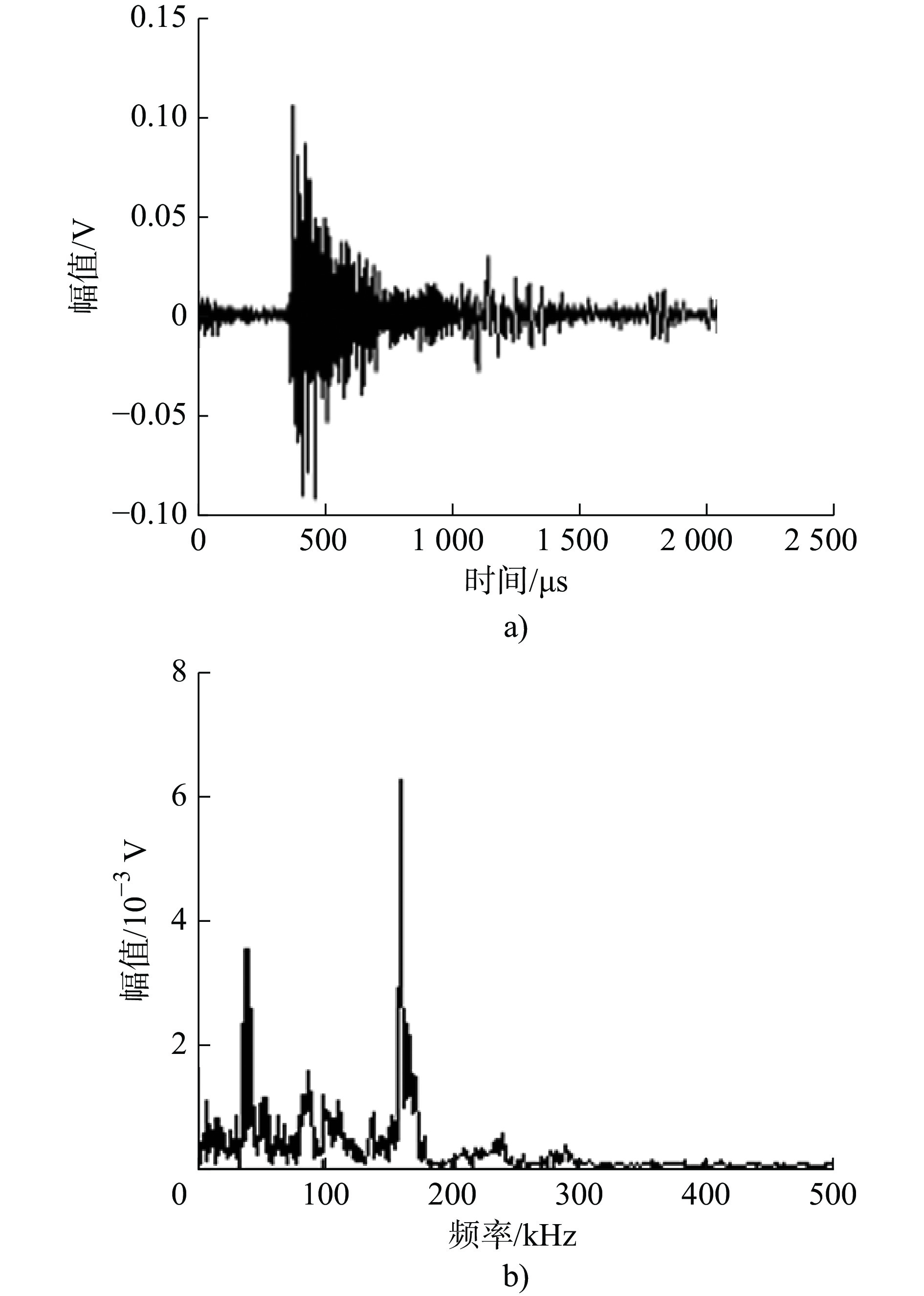
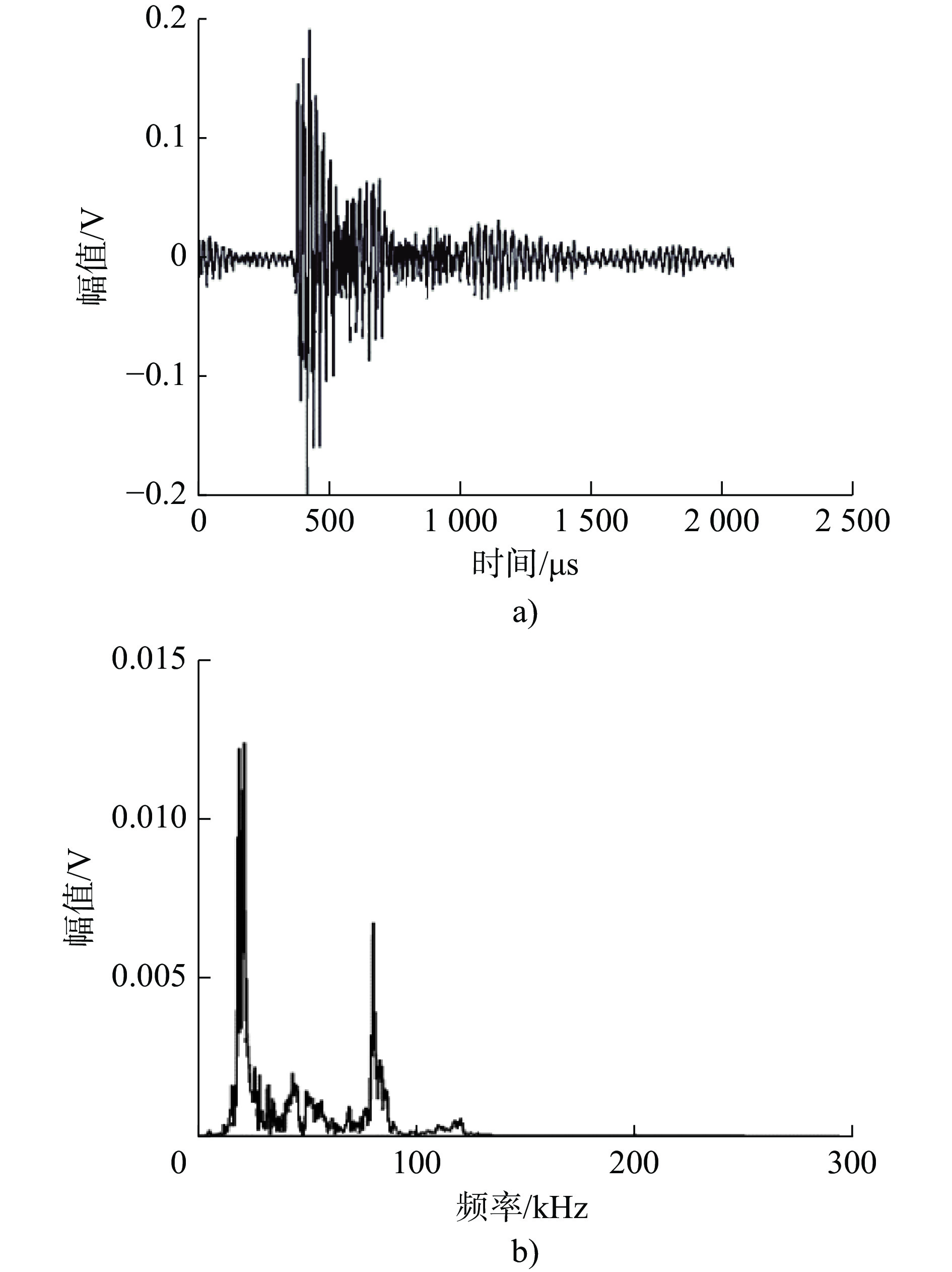
IMF序号 互信息量 IMF序号 互信息量 1 0.6200 5 0.2156 2 0.3548 6 0.2194 3 0.2054 7 0.2252 4 0.3084 8 0.2304 表 5 3种算法降噪后信号的信噪比与均方根误差
Table 5. Signal-to-noise ratio (SNR) and root mean square Error (RMSE) of the denoised signals using three algorithms
降噪算法 均方根误差 信噪比 VMD 13.7352 5.3352 ITD 10.3671 7.5326 (IP)VMD-ITD 4.5521 10.0128 -
[1] 杨永杰, 王德超, 郭明福, 等. 基于三轴压缩声发射试验的岩石损伤特征研究[J]. 岩石力学与工程学报, 2014, 33(1): 98-104. doi: 10.13722/j.cnki.jrme.2014.01.008YANG Y J, WANG D C, GUO M F, et al. Study of rock damage characteristics based on acoustic emission tests under triaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(1): 98-104. (in Chinese) doi: 10.13722/j.cnki.jrme.2014.01.008 [2] 徐奴文, 唐春安, 周钟, 等. 岩石边坡潜在失稳区域微震识别方法[J]. 岩石力学与工程学报, 2011, 30(5): 893-900.XU N W, TANG C A, ZHOU Z, et al. Identification method of potential failure regions of rock slope using microseismic monitoring technique[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(5): 893-900. (in Chinese) [3] 姜万录, 王浩楠, 朱勇, 等. 变分模态分解消噪与核模糊C均值聚类相结合的滚动轴承故障识别方法[J]. 中国机械工程, 2017, 28(10): 1215-1220. doi: 10.3969/j.issn.1004-132X.2017.10.013JIANG W L, WANG H N, ZHU Y, et al. Integrated VMD denoising and KFCM clustering fault identification method of rolling bearings[J]. China Mechanical Engineering, 2017, 28(10): 1215-1220. (in Chinese) doi: 10.3969/j.issn.1004-132X.2017.10.013 [4] 杨宇, 王欢欢, 喻镇涛, 等. 基于ITD改进算法和关联维数的转子故障诊断方法[J]. 振动与冲击, 2012, 31(23): 67-70. doi: 10.3969/j.issn.1000-3835.2012.23.012YANG Y, WANG H H, YU Z T, et al. A rotor fault diagnosis method based on ITD improved algorithm and correlation dimension[J]. Journal of Vibration and Shock, 2012, 31(23): 67-70. (in Chinese) doi: 10.3969/j.issn.1000-3835.2012.23.012 [5] ABDOOS A A, MIANAEI P K, GHADIKOLAEI M R. Combined VMD-SVM based feature selection method for classification of power quality events[J]. Applied Soft Computing, 2016, 38: 637-646. doi: 10.1016/j.asoc.2015.10.038 [6] AN X L, ZHANG F. Pedestal looseness fault diagnosis in a rotating machine based on variational mode decomposition[J]. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2017, 231(13): 2493-2502. doi: 10.1177/0954406216637378 [7] 张雪英, 刘秀丽, 栾忠权. VMD-模平方阈值与PNN相结合的齿轮故障诊断[J]. 机械科学与技术, 2018, 37(12): 1895-1901. doi: 10.13433/j.cnki.1003-8728.20180089ZHANG X Y, LIU X L, LUAN Z Q. Fault diagnosis of gear by using VMD-Modulo square threshold and PNN[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(12): 1895-1901. (in Chinese) doi: 10.13433/j.cnki.1003-8728.20180089 [8] FREI M G, OSORIO I. Intrinsic time-scale decomposition: time-frequency-energy analysis and real-time filtering of non-stationary signals[J]. Proceedings of the Royal Society A:Mathematical, Physical, and Engineering Sciences, 2007, 463(2078): 321-342. doi: 10.1098/rspa.2006.1761 [9] 郭力, 邓喻. 采用遗传算法优化神经网络的铸铁表面粗糙度声发射预测[J]. 机械科学与技术, 2018, 37(10): 1512-1516. doi: 10.13433/j.cnki.1003-8728.20180042GUO L, DENG Y. Acoustic emission monitor grinding surface roughness of cast iron via BP neural networks and genetic algorithm[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(10): 1512-1516. (in Chinese) doi: 10.13433/j.cnki.1003-8728.20180042 [10] 李启月, 王宏伟, 王靖博, 等. 基于EEMD和小波阈值法的爆破振动信号预处理研究[J]. 矿冶工程, 2021, 41(3): 28-31. doi: 10.3969/j.issn.0253-6099.2021.03.007LI Q Y, WANG H W, WANG J B, et al. Pretreatment of blasting vibration signal based on EEMD and wavelet threshold method[J]. Mining and Metallurgical Engineering, 2021, 41(3): 28-31. (in Chinese) doi: 10.3969/j.issn.0253-6099.2021.03.007 [11] LIU Y, ZHANG J H, QIN K J, et al. Diesel engine fault diagnosis using intrinsic time-scale decomposition and multistage Adaboost relevance vector machine[J]. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2018, 232(5): 881-894. doi: 10.1177/0954406217691554 [12] 丛蕊, 苏祥, 武佳奇, 等. 基于ITD和MED的滚动轴承故障特征提取方法[J]. 煤矿机械, 2018, 39(6): 138-141. doi: 10.13436/j.mkjx.201806052CONG R, SU X, WU J Q, et al. Fault feature extraction method of rolling bearing based on ITD and MED[J]. Coal Mine Machinery, 2018, 39(6): 138-141. (in Chinese) doi: 10.13436/j.mkjx.201806052 [13] GUO Z X, LEI X, YE T H, et al. Online detection of time-variant oscillations based on improved ITD[J]. Control Engineering Practice, 2014, 32: 64-72. doi: 10.1016/j.conengprac.2014.07.002 [14] YONG X. Blind source separation based on constant modulus criterion and signal mutual information[J]. Computers & Electrical Engineering, 2008, 34(5): 416-422. [15] 刘婷婷, 张迪, 王雪梅, 等. 基于VMD及模糊相关分类器的滚动轴承故障诊断[J]. 机械设计与制造, 2019(2): 222-225. doi: 10.3969/j.issn.1001-3997.2019.02.056LIU T T, ZHANG D, WANG X M, et al. Fault diagnosis of ball bearing based on VMD and ACC[J]. Machinery Design & Manufacture, 2019(2): 222-225. (in Chinese) doi: 10.3969/j.issn.1001-3997.2019.02.056 [16] ZHANG J, HE J J, LONG J C, et al. A new denoising method for UHF PD signals using adaptive VMD and SSA-Based shrinkage method[J]. Sensors, 2019, 19(7): 1594. doi: 10.3390/s19071594 [17] 张运东. 基于FVMD多尺度排列熵和GK模糊聚类的故障诊断方法[D]. 秦皇岛: 燕山大学, 2017ZHANG Y D. A method of fault diagnosis based on FVMD multi-scale permutation entropy and GK fuzzy clustering[D]. Qinhuangdao: Yanshan University, 2017. (in Chinese) [18] MITRAKOVIĆ D, GRABEC I, SEDMAK S. Simulation of AE signals and signal analysis systems[J]. Ultrasonics, 1985, 23(5): 227-232. doi: 10.1016/0041-624X(85)90018-6 [19] 白瑞. 基于声发射的旋转机械故障诊断[D]. 沈阳: 沈阳工业大学, 2017BAI R. Rotating machinery fault diagnosis based on acoustic emission technology[D]. Shenyang: Shenyang University of Technology, 2017. (in Chinese) -







 下载:
下载: