Application of Improved Particle Swarm Algorithm in Vehicle LQR Semi-active Suspension
-
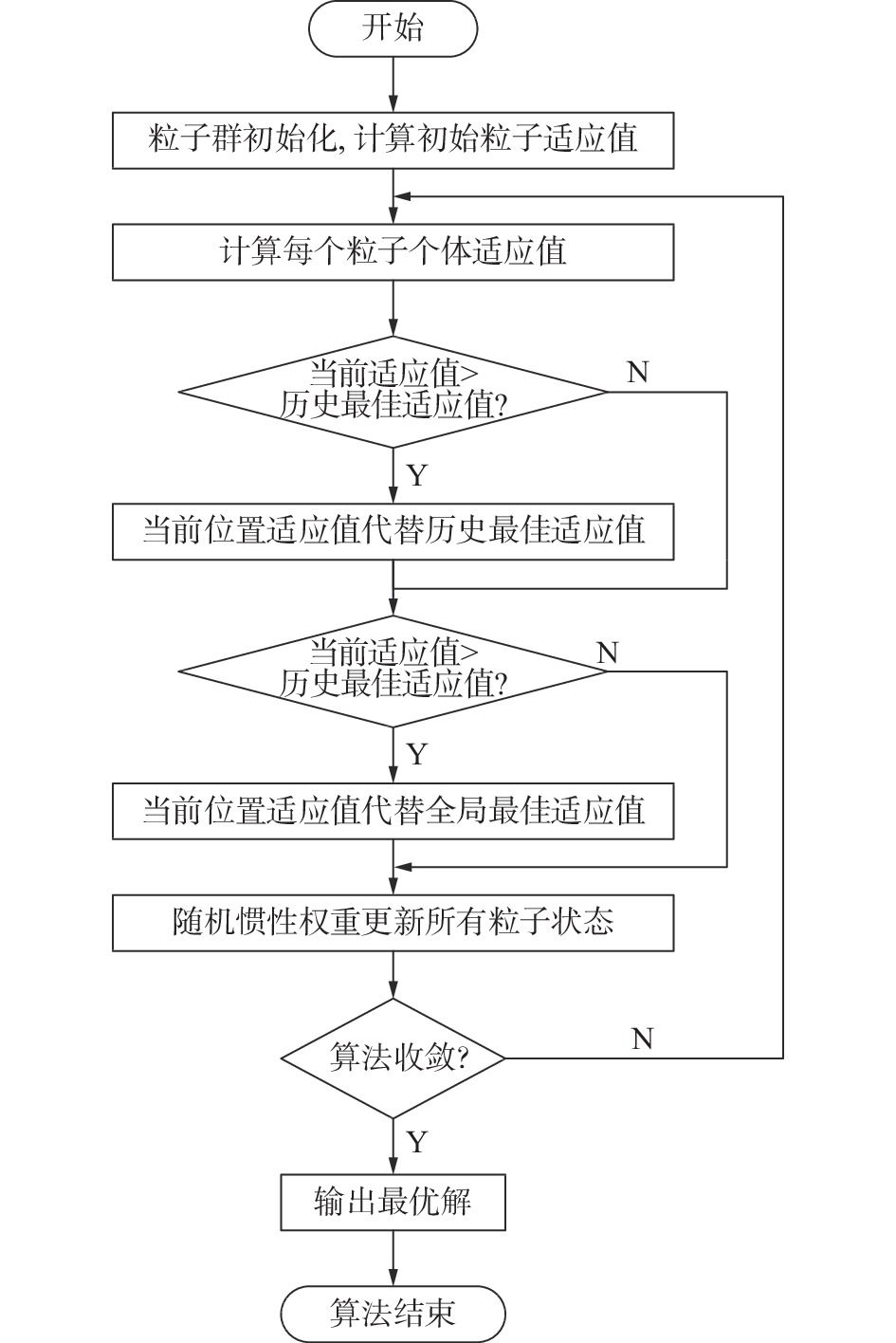
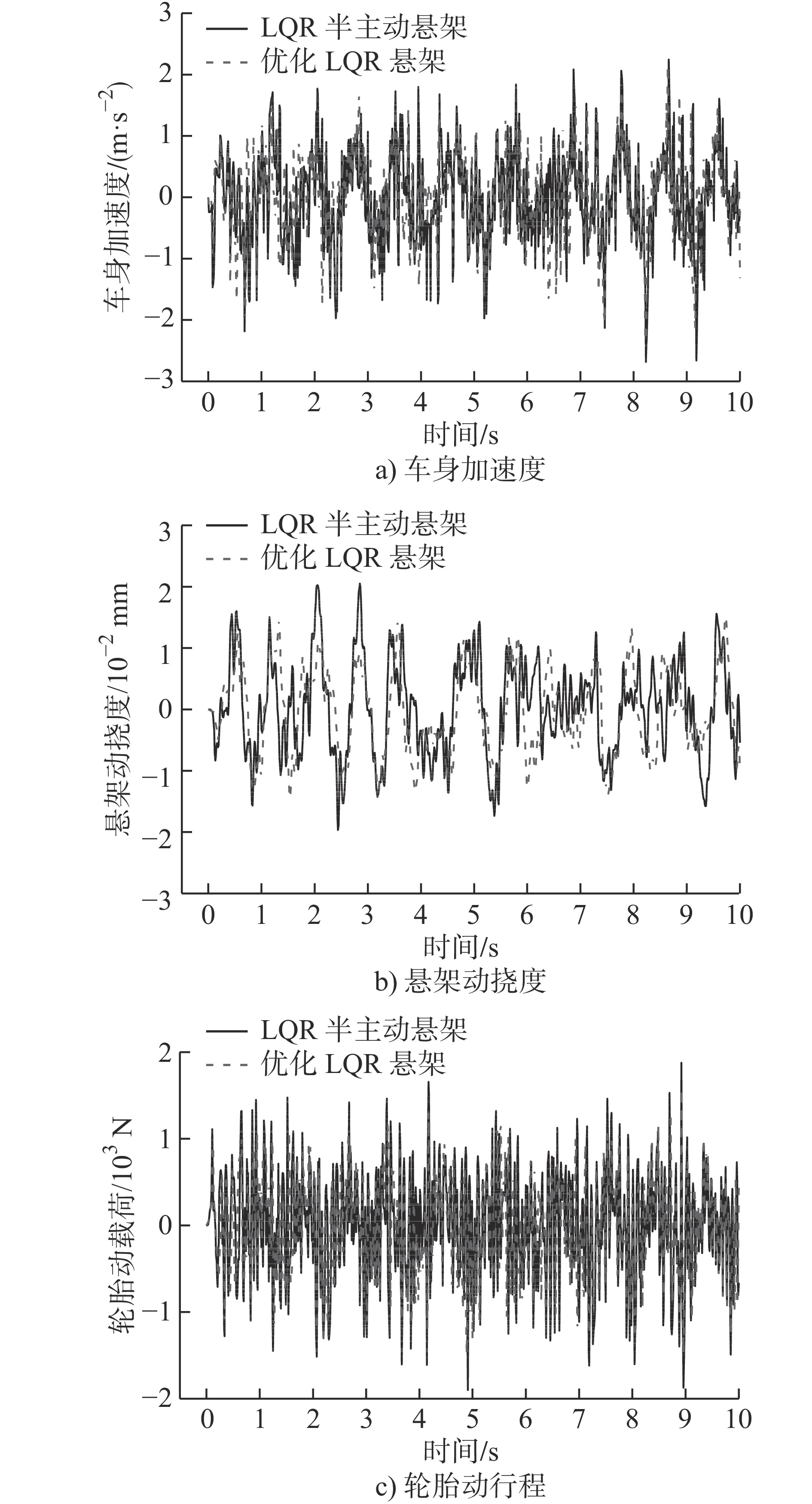
摘要: 针对车辆半主动悬架LQR控制中Q矩阵和R矩阵往往由经验取值的问题,提出一种基于改进粒子群算法的LQR控制方法。该算法采用随机惯性权重代替了传统粒子群算法的固定惯性权重,提高了求解精度和效率,得到了更加具有适应性的LQR控制矩阵系数。为验证此方法的有效性,基于天棚阻尼模型建立1/4车被动悬架模型和半主动悬架模型,利用线性二次最优控制建立LQR控制器,并利用优化算法得到新的控制矩阵。通过仿真对比被动悬架、LQR控制的LQR半主动悬架、改进粒子群算法优化后的优化LQR悬架的各项性能参数,发现优化LQR悬架在悬架动挠度没有受到影响的前提下,使车辆的垂向加速度和轮胎动载荷得到有效降低,提高了车辆的行驶平顺性和操纵安全性。Abstract: Aiming at the problem that the Q matrix and R matrix in the LQR control of vehicle semi-active suspensions are often valued by personal experience, an LQR control method based on an improved particle swarm algorithm is proposed. The algorithm uses random inertia weights instead of the fixed inertia weights of the traditional particle swarm algorithm, improves the accuracy and efficiency of the solution, and obtains more adaptive LQR control matrix coefficients. In order to verify the effectiveness of this method, a quarter-car passive suspension model and a semi-active suspension model are established based on the ceiling damping model, the LQR controller is established using linear quadratic optimal control, and the new control matrix is obtained using the optimization algorithm. Through simulation and comparison of various performance parameters of passive suspension, LQR semi-active suspension controlled by LQR, and optimized LQR suspension optimized by improved particle swarm algorithm, it is found that the optimized LQR suspension effectively reduces the vertical acceleration of the vehicle and the dynamic load of the tire on the premise that the dynamic deflection of the suspension is not affected, and improves the driving comfort and handling safety of the vehicle.
-
Key words:
- semi-active suspension /
- LQR control /
- particle swarm algorithm /
- ride comfort
-
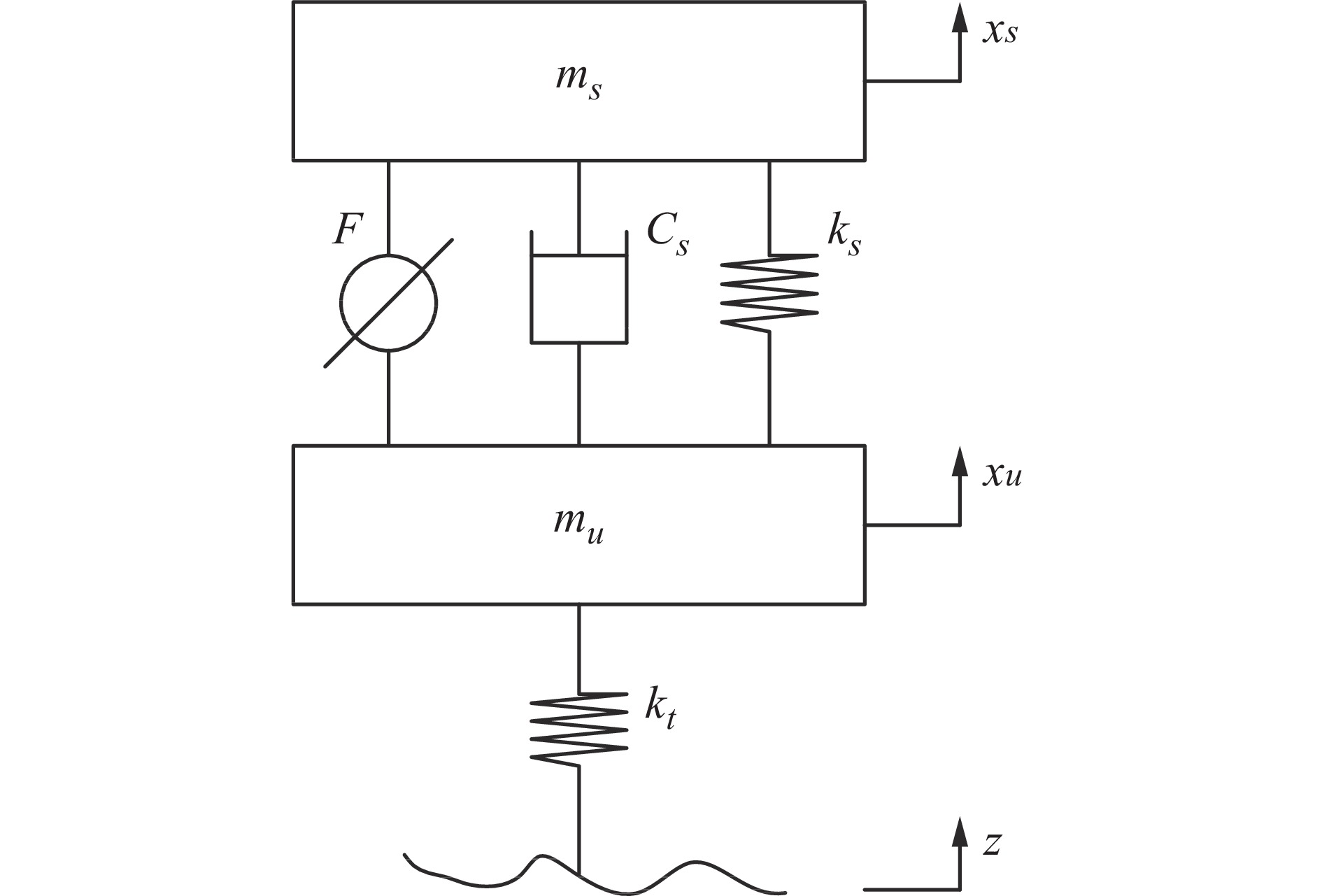
表 1 四分之一车仿真参数
模型参数 数值 簧载质量ms 380 kg 非簧载质量mu 40 kg 弹簧刚度ks 20 000 N/m 轮胎刚度kt 250 000 N/m 阻尼器阻尼系数Cs 1 500 N·s/m 下截止频率f0 0.1 Hz 表 2 各项评价指标的均方根值
参数 被动悬架 LQR半主动悬架 优化LQR悬架 车身加速度 0.999 069 0.774 814 0.707 692 悬架动挠度 8.88376 × 10−3 7.49789 × 10−3 6.81384 × 10−3 轮胎动载荷 737.6 601.9 544.3 -
[1] 张俊红, 洪刘生, 杨文钊, 等. 车辆悬架系统及其性能评价综述[J]. 机械设计与研究, 2015, 31(6): 147-153. doi: 10.13952/j.cnki.jofmdr.2015.0251ZHANG J H, HONG L S, YANG W Z, et al. Review of technique application and performance evaluation for the vehicle suspension system[J]. Machine Design and Research, 2015, 31(6): 147-153. (in Chinese) doi: 10.13952/j.cnki.jofmdr.2015.0251 [2] KIM H, YOON Y S. Semi-active suspension with preview using a frequency-shaped performance index[J]. Vehicle System Dynamics, 1995, 24(10): 759-780. doi: 10.1080/00423119508969117 [3] 徐明, 黄庆生, 李刚. 车辆半主动悬架智能控制方法研究现状[J]. 机床与液压, 2021, 49(1): 169-174. doi: 10.3969/j.issn.1001-3881.2021.01.034XU M, HUANG Q S, LI G. Research status of intelligent control method for vehicle semi-active suspension[J]. Machine Tool and Hydraulics, 2021, 49(1): 169-174. (in Chinese) doi: 10.3969/j.issn.1001-3881.2021.01.034 [4] 朱华. 半主动悬架的研究现状与发展趋势[J]. 城市车辆, 2009(4): 38-40.ZHU H. Development and trend of semi-active suspensions[J]. Urban Vehicles, 2009(4): 38-40. (in Chinese) [5] 徐旭, 杨晓峰, 沈钰杰, 等. 基于滞后型系统理论的半主动悬架控制系统稳定性分析[J]. 振动与冲击, 2021, 40(7): 208-215. doi: 10.13465/j.cnki.jvs.2021.07.028XU X, YANG X F, SHEN Y J, et al. Stability analysis of semi-active suspension control system based on hysteresis system theory[J]. Journal of Vibration and Shock, 2021, 40(7): 208-215. (in Chinese) doi: 10.13465/j.cnki.jvs.2021.07.028 [6] 赵强, 张娜, 岳永恒. 基于惯容器的半主动座椅悬架控制和优化[J]. 控制工程, 2019, 26(12): 2311-2316. doi: 10.14107/j.cnki.kzgc.161273ZHAO Q, ZHANG N, YUE Y H. Control and optimization of semi-active seat suspension based on inerter[J]. Control Engineering of China, 2019, 26(12): 2311-2316. (in Chinese) doi: 10.14107/j.cnki.kzgc.161273 [7] KARNOPP D. Design principles for vibration control systems using semi-active dampers[J]. Journal of Dynamic Systems, Measurement, and Control, 1990, 112(3): 448-455. doi: 10.1115/1.2896163 [8] 张磊, 张进秋, 彭志召, 等. 车辆半主动悬架改进型天棚阻尼控制算法[J]. 汽车工程, 2015, 37(8): 931-935. doi: 10.3969/j.issn.1000-680X.2015.08.012ZHANG L, ZHANG J Q, PENG Z Z, et al. Improved sky-hook damping control algorithm for semi-active vehicle suspensions[J]. Automotive Engineering, 2015, 37(8): 931-935. (in Chinese) doi: 10.3969/j.issn.1000-680X.2015.08.012 [9] 赵强, 何法, 王鑫, 等. 基于遗传算法优化的车辆主动悬架模糊PID控制[J]. 重庆理工大学学报(自然科学), 2016, 30(2): 6-11.ZHAO Q, HE F, WANG X, et al. Fuzzy-PID control of vehicle active suspension based on genetic algorithm optimization[J]. Journal of Chongqing University of Technology (Natural Science), 2016, 30(2): 6-11. (in Chinese) [10] 樊智敏, 王宝林, 樊宇. 基于粒子群算法的车辆半主动悬架模糊PID控制的优化研究[J]. 机械与电子, 2020, 38(11): 76-80. doi: 10.3969/j.issn.1001-2257.2020.11.016FAN Z M, WANG B L, FAN Y. Research on the optimization of fuzzy PID control of vehicle semi-active suspension based on particle swarm optimization[J]. Machinery and Electronics, 2020, 38(11): 76-80. (in Chinese) doi: 10.3969/j.issn.1001-2257.2020.11.016 [11] 张勇. 半主动座椅悬架非线性控制研究[D]. 长春: 吉林大学, 2019ZHANG Y. Research on nonlinear control of semi-active seat suspension[D]. Changchun: Jilin University, 2019. (in Chinese) [12] 张志飞, 刘建利, 徐中明, 等. 基于改进层次分析法的半主动悬架LQG控制器的设计[J]. 汽车工程, 2012, 34(6): 528-533. doi: 10.3969/j.issn.1000-680X.2012.06.011ZHANG Z F, LIU J L, XU Z M, et al. Design of LQG controller for semi-active suspension based on improved analytic hierarchy process[J]. Automotive Engineering, 2012, 34(6): 528-533. (in Chinese) doi: 10.3969/j.issn.1000-680X.2012.06.011 [13] 彭志召, 张进秋, 张雨, 等. 车辆半主动悬挂的频域控制算法[J]. 装甲兵工程学院学报, 2013, 27(4): 36-42 + 50.PENG Z Z, ZHANG J Q, ZHANG Y, et al. Frequency domain control algorithm for semi-active suspension of vehicles[J]. Journal of Academy of Armored Force Engineering, 2013, 27(4): 36-42 + 50. (in Chinese) [14] 来飞, 胡博. 汽车主动悬架技术的研究现状[J]. 南京理工大学学报, 2019, 43(4): 518-526. doi: 10.14177/j.cnki.32-1397n.2019.43.04.020LAI F, HU B. Research status of automotive active suspension technology[J]. Journal of Nanjing University of Science and Technology, 2019, 43(4): 518-526. (in Chinese) doi: 10.14177/j.cnki.32-1397n.2019.43.04.020 [15] THOMPSON A G. An active suspension with optimal linear state feedback[J]. Vehicle System Dynamics, 1976, 5(4): 187-203. doi: 10.1080/00423117608968414 [16] PRASAD L B, TYAGI B, GUPTA H O. Optimal control of nonlinear inverted pendulum system using PID controller and LQR: Performance analysis without and with disturbance input[J]. International Journal of Automation and Computing, 2014, 11(6): 661-670. doi: 10.1007/s11633-014-0818-1 -








 下载:
下载: