多带隙联合的声子晶体滤波梁弹性波传播特性

张鑫浩; 赵才友; 郑钧元; 牛亚文; 未娜超

doi:10.13433/j.cnki.1003-8728.20200629

多带隙联合的声子晶体滤波梁弹性波传播特性

doi: 10.13433/j.cnki.1003-8728.20200629

张鑫浩^{1, 2, 3,},
赵才友^{1, 2, ,},
郑钧元^{1, 2},
牛亚文^{1, 2},
未娜超^{1, 2}

1.
西南交通大学土木工程学院，成都　610031
2.
西南交通大学高速铁路线路工程教育部重点实验室，成都　610031
3.
西南交通大学唐山研究院，河北唐山　063000

基金项目: 国家自然科学基金面上项目（51978585）、高速铁路基础研究联合基金项目（U1734207）及四川省应用基础研究项目（2020YJ0214）

详细信息

作者简介:
张鑫浩（1996−），硕士研究生，研究方向为铁路轨道周期结构减振降噪，736948278@qq.com

通讯作者:
赵才友，教授，博士生导师，zcy848279@qq.com

中图分类号: MU211
计量
- 文章访问数: 154
- HTML全文浏览量: 53
- PDF下载量: 25
- 被引次数: 0
出版历程
- 收稿日期: 2021-05-14
- 网络出版日期: 2023-04-21
- 刊出日期: 2023-03-25

Elastic Wave Propagation Characteristics of a Combined Multi Band Gap Phononic Crystal Filter Beam

ZHANG Xinhao^{1, 2, 3
,},
ZHAO Caiyou^{1, 2
, ,},
ZHENG Junyuan^{1, 2},
NIU Yawen^{1, 2},
WEI Nachao^{1, 2}

1.
School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China
2.
The Ministry of Education Key Laboratory of High Speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China
3.
Tangshan Institute, Southwest Jiaotong University, Tangshan 063000, Hebei, China

摘要

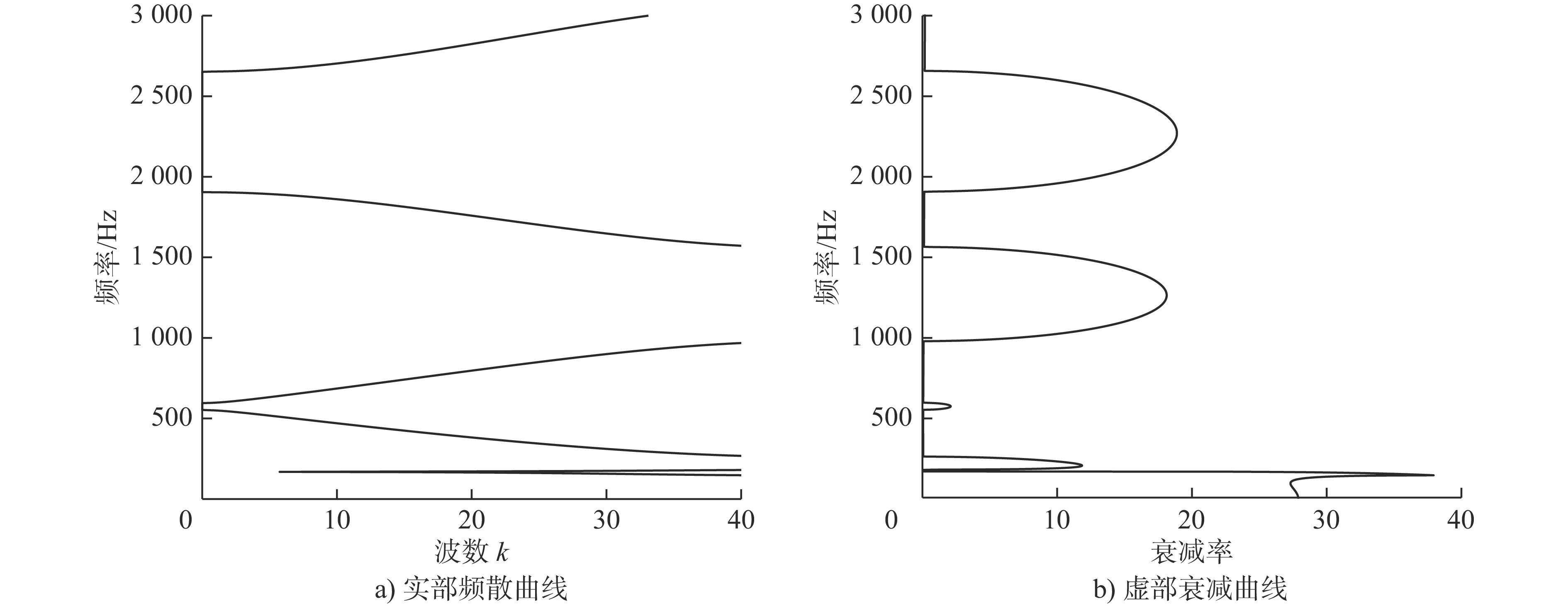
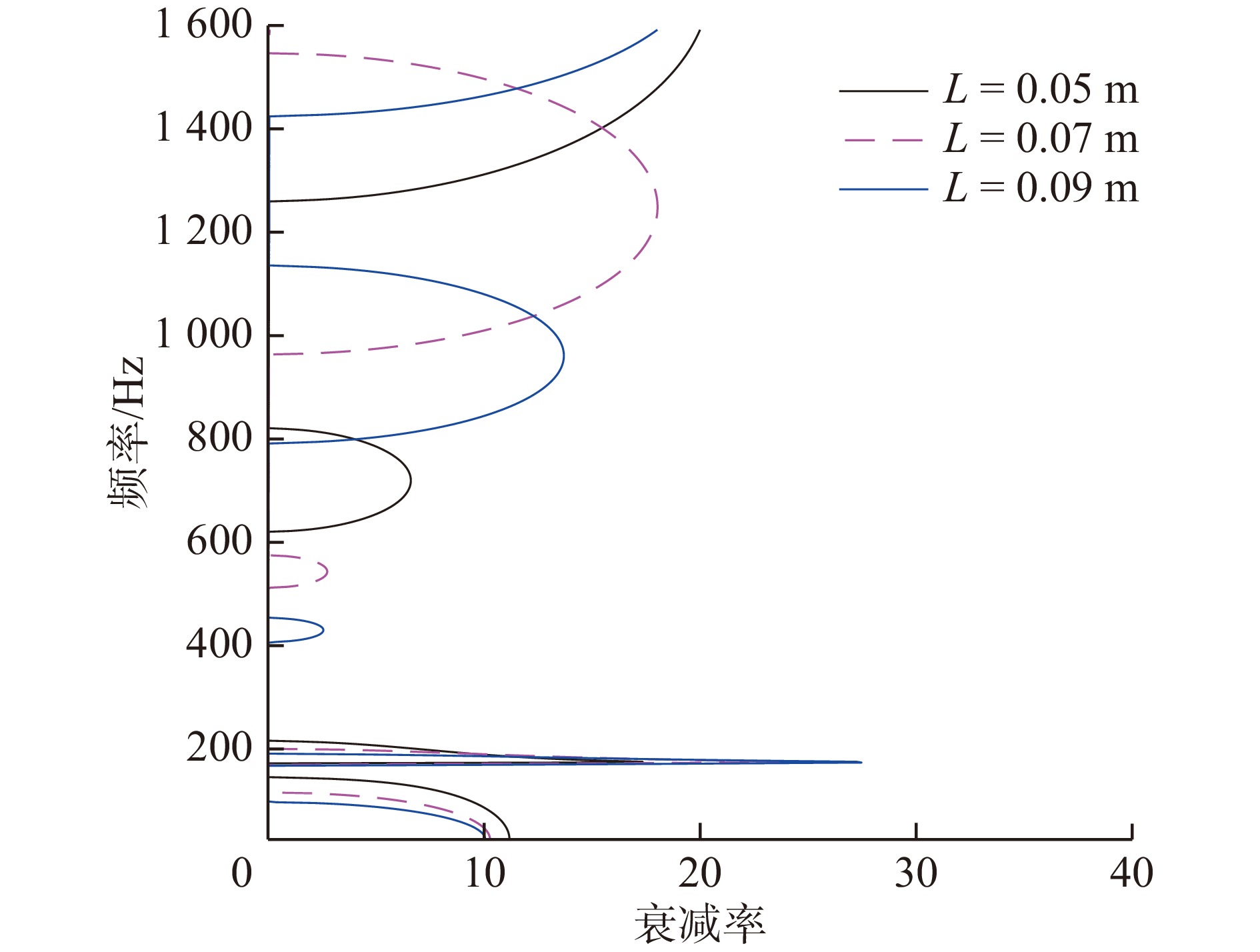
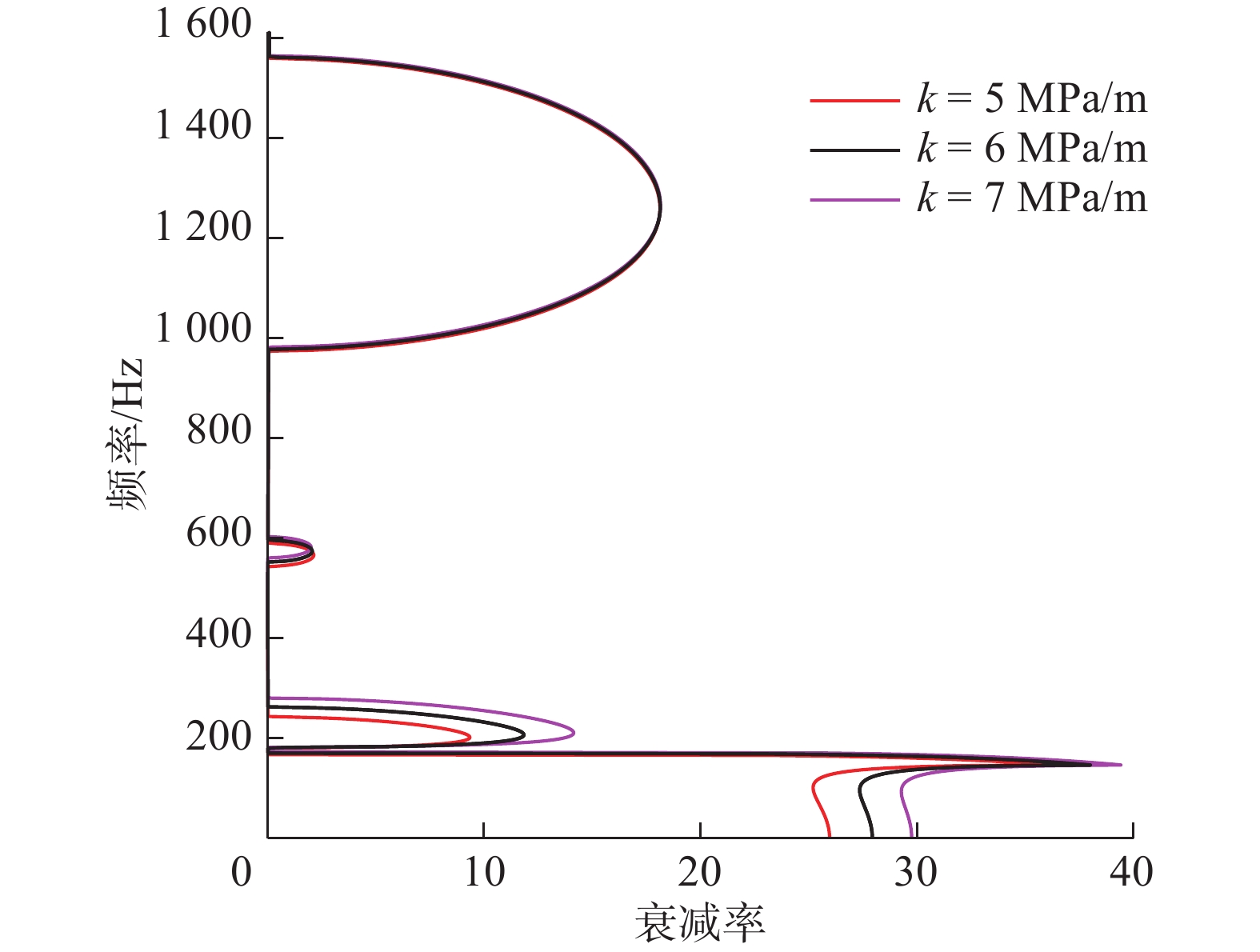
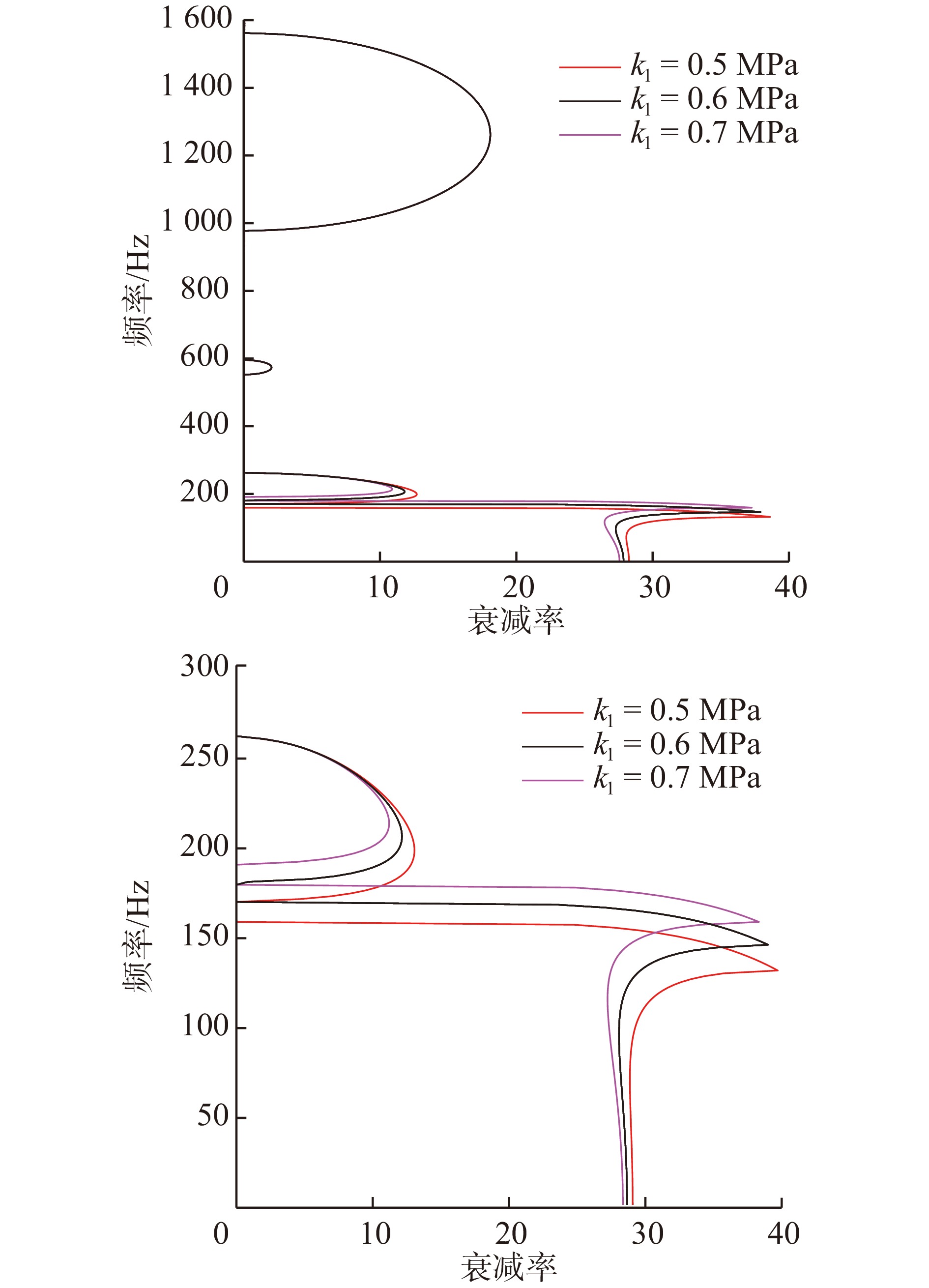
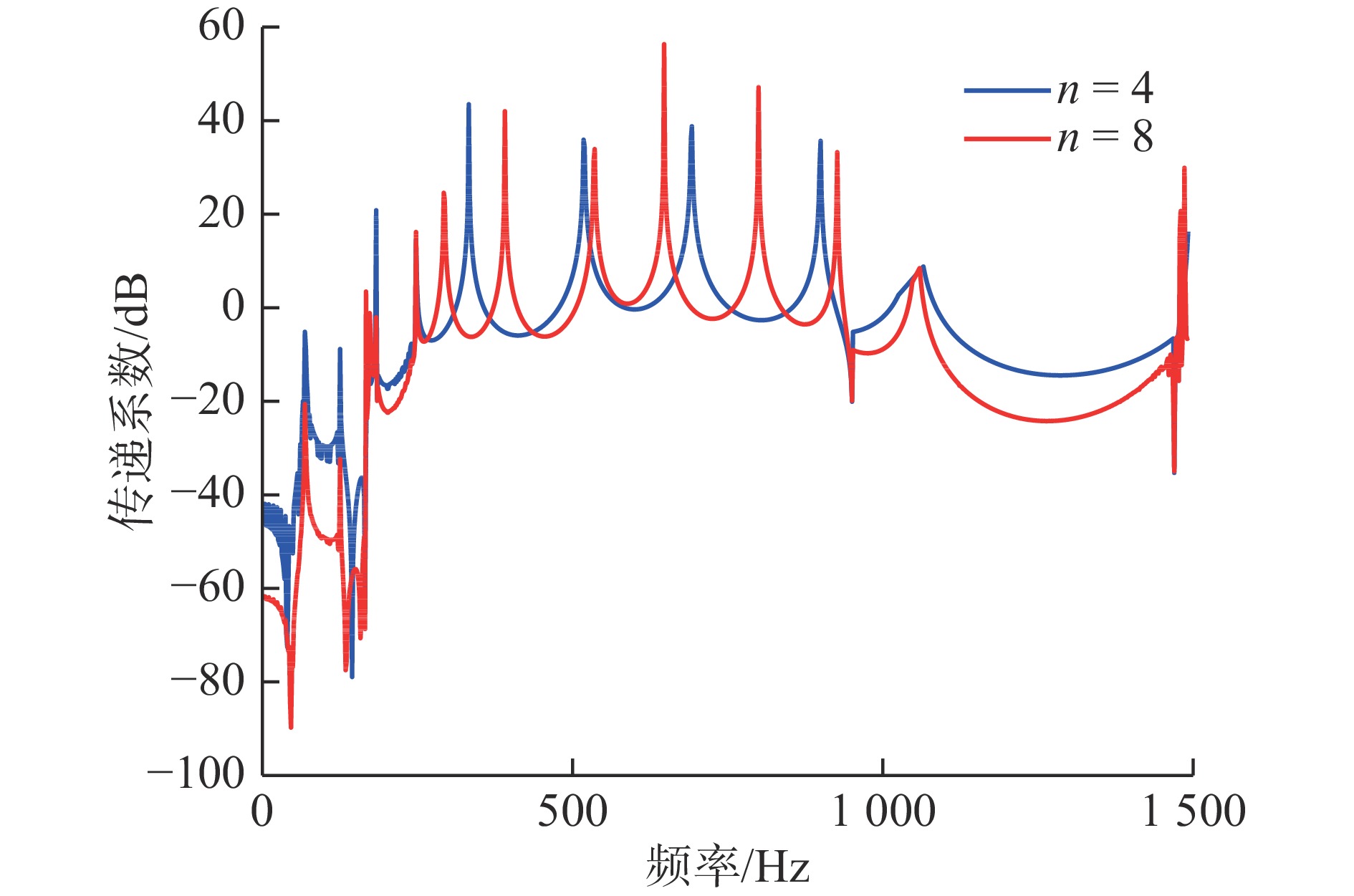
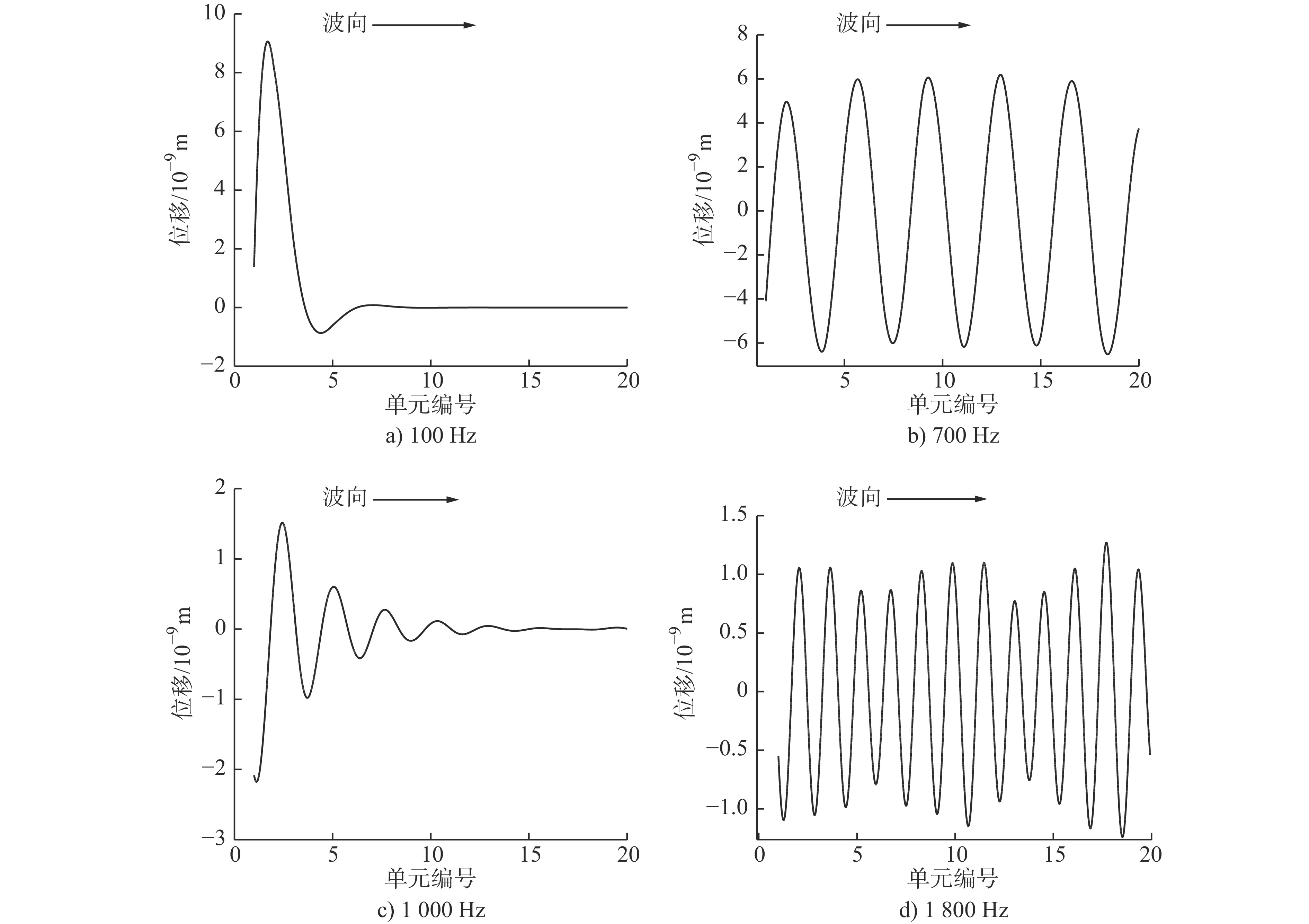
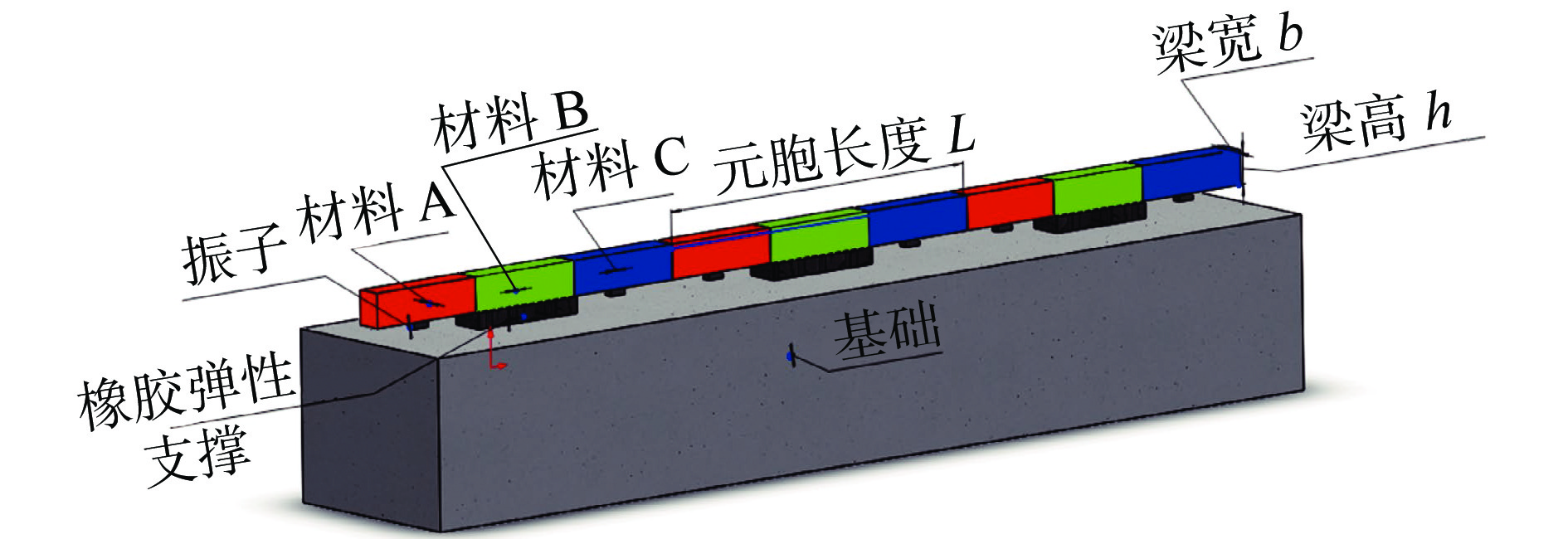
摘要: 提出了一种包含Bragg散射、整体局域共振和局部局域共振机理的多带隙联合声子晶体滤波梁，通过传递矩阵法与Bloch定理求得无限周期结构各阶带隙为0 ~ 170 Hz、180 ~ 262.6 Hz、552.3 ~ 597 Hz、974 ~ 1 563 Hz、1 903 ~ 2 667 Hz；并调节结构参数，得出带隙调制规律和带隙机理。同时，与其他3种工况声子晶体梁带隙特征进行对比分析，证明了声子晶体滤波梁在带隙宽度、丰富度以及弹性波衰减率方面均有着相对优势，具备更好的过滤或抑制结构中弹性波的性能。此外，求解近声子晶体滤波梁的振动传递系数，得出在各阶带隙范围内，弹性波的传播存在明显衰减，验证了带隙的存在。最后为探究弹性波在带隙/通带范围内的波动模式，分别提取位于带隙/通带范围梁体位移分布，发现在带隙频率范围内的弹性波沿波动方向快速衰减，表现出带隙特性；通带频率范围内的弹性波无明显变化或衰减，表现出通带特性。
- 声子晶体滤波梁 /
- 弹性波 /
- 带隙联合 /
- 振动传递特性 /
- 传递矩阵法
Abstract: In this paper, a multi-band gap joint phononic crystal filter beam is proposed, which is includes Bragg Diffraction, entire local resonance and partial local resonance. By means of Transfer Matrix and Bloch theorem, it is found that the band gaps of infinite periodic structures are 0 ~ 170 Hz, 180 ~ 262.6 Hz, 552.3 ~ 597 Hz, 974 ~ 1 563 Hz and 1 903 ~ 2 667 Hz. And the modulating law and mechanism of band gap are obtained by changing the structural parameters. At the same time, compared with the band gap characteristics of the traditional three-component and other three working conditions, it is proved that the phononic crystal filter beam has relative advantages in band gap width, richness and elastic wave attenuation rate. That’ to say, phononic crystal filter beam has better performance of filtering and suppressing elastic waves in the structure. In addition, the vibration transfer coefficient of near-phononic crystal filter beam is calculated, and it is concluded that the elastic wave propagation attenuates obviously in the range of each band gap, which verifies the existence of the band gap. In the last part, in order to find out the wave modes of elastic wave in the band gap and in the passband range, the displacement distribution of the beam in band gap and passband range is extracted respectively.From the result, it is found that the elastic wave in band gap frequency range attenuates rapidly along the wave direction, showing the characteristics of band gap. While the elastic wave in the frequency range of passband has no obvious change or attenuation, showing the characteristics of passband. To sum up, this structure provides a new idea and theoretical support for the subsequent apply of phononic crystals to reduce vibration and noise of beam structures.
- phononic crystal filter beam /
- elastic wave /
- band gap combination /
- vibration transfer characteristics /
- transfer matrix method

HTML全文

图 1 声子晶体滤波梁实际理想模型

下载: 全尺寸图片幻灯片

图 2 声子晶体滤波梁及元胞理论模型

下载: 全尺寸图片幻灯片

图 3 声子晶体滤波梁带隙图

下载: 全尺寸图片幻灯片

图 4 不同工况的梁元胞模型

下载: 全尺寸图片幻灯片

图 5 不同工况下的带隙对比图

下载: 全尺寸图片幻灯片

图 6 元胞支撑段长度对带隙的影响

下载: 全尺寸图片幻灯片

图 7 连续弹性支撑刚度k对带隙的影响

下载: 全尺寸图片幻灯片

图 8 弹簧振子刚度k₁对带隙的影响

下载: 全尺寸图片幻灯片

图 9 近声子晶体滤波梁的振动传递曲线

下载: 全尺寸图片幻灯片

图 10 通带/带隙频率范围内梁体位移分布（位置0.21 m）

下载: 全尺寸图片幻灯片

表 1 声子晶体滤波梁的结构及材料参数

名称	A	B	C
材料	钢	铝	铅
弹性模量/GPa	206	71.7	17
剪切模量/GPa	79.4	26	7
密度/（kg·m⁻³）	7850	2699	11300
泊松量	0.29	0.33	0.42
波束宽度/m	0.015	0.015	0.015
波束高度/m	0.02	0.02	0.02
波束长度/m	0.07	0.07	0.07
剪切系数	0.8	0.8	0.8

下载: 导出CSV

表 2 带隙汇总表 Hz

带隙	滤波梁	工况1	工况2	工况3
1阶	0 ~ 170	91 ~ 200	0 ~ 97.8	0 ~ 92.31
2阶	180 ~ 262.6	526.8 ~ 743.3	163.7 ~ 211	146.4 ~ 176.7
3阶	552.3 ~ 597	1214 ~ 1593	542.7 ~ 756	492 ~ 558.6
4阶	974 ~ 1563	1903 ~ 2667	1221 ~ 1635	947 ~ 1545
5阶	1903 ~ 2667	0	2198 ~ 2803	1903 ~ 2667
总带宽	1650.3	1468.8	1337.4	1551.21

下载: 导出CSV

参考文献(21)

[1]	KHELIF A, ADIBI A. Phononic crystals: fundamentals and applications[M]. Berlin: Springer, 2016
[2]	YUAN B, WEN J H, WEN X S. Oblique incidence properties of locally resonant sonic materials with resonance and Bragg scattering effects[J]. Chinese Physics B, 2013, 22(7): 074302. doi: 10.1088/1674-1056/22/7/074302
[3]	LI L, WEN J H, CAI L, et al. Acoustic scattering from a submerged cylindrical shell coated with locally resonant acoustic metamaterials[J]. Chinese Physics B, 2013, 22(1): 014301. doi: 10.1088/1674-1056/22/1/014301
[4]	CHEN S B, WEN J H, YU D L, et al. Band gap control of phononic beam with negative capacitance piezoelectric shunt[J]. Chinese Physics B, 2011, 20(1): 014301. doi: 10.1088/1674-1056/20/1/014301
[5]	沈惠杰, 温激鸿, 郁殿龙, 等. 基于Timoshenko梁模型的周期充液管路弯曲振动带隙特性和传输特性[J]. 物理学报, 2009, 58(12): 8357-8363. doi: 10.3321/j.issn:1000-3290.2009.12.038 SHEN H J, WEN J H, YU D L, et al. Flexural vibration property of periodic pipe system conveying fluid based on Timoshenko beam equation[J]. Acta Physica Sinica, 2009, 58(12): 8357-8363. (in Chinese) doi: 10.3321/j.issn:1000-3290.2009.12.038
[6]	温激鸿, 王刚, 郁殿龙, 等. 声子晶体振动带隙及减振特性研究[J]. 中国科学 E辑:技术科学, 2008, 51(1): 85-99. doi: 10.1007/s11431-008-0008-x WEN J H, WANG G, YU D L, et al. Study on the vibration band gap and vibration attenuation property of phononic crystals[J]. Science in China Series E:Technological Sciences, 2008, 51(1): 85-99. (in Chinese) doi: 10.1007/s11431-008-0008-x
[7]	YU D L, WEN J H, ZHAO H, et al. Vibration reduction by using the idea of phononic crystals in a pipe-conveying fluid[J]. Journal of Sound and Vibration, 2008, 318(1-2): 193-205. doi: 10.1016/j.jsv.2008.04.009
[8]	WANG P, YI Q, ZHAO C Y, et al. Wave propagation in periodic track structures: band-gap behaviours and formation mechanisms[J]. Archive of Applied Mechanics, 2017, 87(3): 503-519. doi: 10.1007/s00419-016-1207-8
[9]	易强, 王平, 赵才友, 等. 有砟轨道结构弹性波传播特性研究[J]. 铁道学报, 2019, 41(6): 137-145. doi: 10.3969/j.issn.1001-8360.2019.06.019 YI Q, WANG P, ZHAO C Y, et al. Study on elastic wave propagation properties of ballast track structure[J]. Journal of the China Railway Society, 2019, 41(6): 137-145. (in Chinese) doi: 10.3969/j.issn.1001-8360.2019.06.019
[10]	WANG P, YI Q, ZHAO C Y, et al. Wave propagation control in periodic track structure through local resonance mechanism[J]. Journal of Central South University, 2018, 25(12): 3062-3074. doi: 10.1007/s11771-018-3974-6
[11]	易强, 王宇航, 高鑫, 等. 轨道交通周期型声屏障带隙特性及其降噪性能[J]. 中南大学学报(自然科学版), 2019, 50(5): 1263-1270. YI Q, WANG Y H, GAO X, et al. Band gap properties and noise reduction performances of periodic noise barriers in rail transit[J]. Journal of Central South University (Science and Technology), 2019, 50(5): 1263-1270. (in Chinese)
[12]	GENG Q, WANG T, WU L, et al. Defect coupling behavior and flexural wave energy harvesting of phononic crystal beams with double defects in thermal environments[J]. Journal of Physics D:Applied Physics, 2021, 54(22): 225501. doi: 10.1088/1361-6463/abe1e7
[13]	CUI R X, ZHOU J S, GONG D. Band gap and vibration reduction properties of damped rail with two-dimensional honeycomb phononic crystals[J]. Shock and Vibration, 2021, 2021: 8814962.
[14]	HE F Y, QIAN D H, ZHAI M S. Wave propagation in a non-local piezoelectric phononic crystal Timoshenko nanobeam[J]. Modern Physics Letters B, 2021, 35(3): 2150064. doi: 10.1142/S0217984921500640
[15]	CHIN E B, MOKHTARI A A, SRIVASTAVA A, et al. Spectral extended finite element method for band structure calculations in phononic crystals[J]. Journal of Computational Physics, 2021, 427: 110066. doi: 10.1016/j.jcp.2020.110066
[16]	CHEN Z Y, WANG G F, ZHOU W J, et al. Elastic foundation induced wide bandgaps for actively-tuned topologically protected wave propagation in phononic crystal beams[J]. International Journal of Mechanical Sciences, 2021, 194: 106215. doi: 10.1016/j.ijmecsci.2020.106215
[17]	CANTANHÊDE H V, MIRANDA E J P JR, DOS SANTOS J M C. Elastic wave propagation in a bio-inspired phononic crystal[J]. Materials Science Forum, 2020, 1012: 9-13. doi: 10.4028/www.scientific.net/MSF.1012.9
[18]	冯青松, 杨舟, 郭文杰, 等. 周期离散支承钢轨垂向振动带隙特性分析[J]. 中国科学: 技术科学, 2020, 50(12): 1563-1576. doi: 10.1360/SST-2019-0271 FENG Q S, YANG Z, GUO W J, et al. Analysis of vertical vibration band gap characteristics of periodic discrete support rail[J]. Scientia Sinica Technologica, 2020, 50(12): 1563-1576. (in Chinese) doi: 10.1360/SST-2019-0271
[19]	冯青松, 杨舟, 梁玉雄, 等. 长度调制的声子晶体梁弯曲振动带隙特性分析[J]. 噪声与振动控制, 2020, 40(4): 1-8. FENG Q S, YANG Z, LIANG Y X, et al. Analysis of the bending vibration band gap characteristics of a length-adjustable phononic crystal beam[J]. Noise and Vibration Control, 2020, 40(4): 1-8. (in Chinese)
[20]	冯青松, 杨舟, 梁玉雄, 等. 双周期声子晶体梁弯曲振动带隙特性分析[J]. 噪声与振动控制, 2020, 40(3): 1-7 + 32. FENG Q S, YANG Z, LIANG Y X, et al. Study on bending vibration band gap characteristics of a double periodic phononic crystal beam[J]. Noise and Vibration Control, 2020, 40(3): 1-7 + 32. (in Chinese)
[21]	NORTON M P, KARCZUB D G. Fundamentals of noise and vibration analysis for engineers[M]. Cambridge: Cambridge University Press, 2003