Analyzing Vortex Phenomenon of High-speed Gear Shafting System and Its Critical Speed with Gyroscopic Effect Considered
-
摘要: 高速齿轮轴系由于不平衡量等因素受陀螺效应会产生较大弯矩存在潜在共振危险,计及转轴及齿轮轮体陀螺效应,分别采用梁单元法和有限元法建立某型共轴高速直升机传动系统高速输入轴系模型,系统研究高速齿轮轴系不同振型的涡动现象,结合临界转速坎贝尔图,对比自由与约束模态和约束模态下不同轴承刚度对临界转速数值影响。结果表明:高速齿轮轴系扭转和伸缩振型在自由及约束模态均不会产生涡动,弯曲、节径等横向振型产生明显涡动现象,且在约束模态下涡动现象减弱;临界转速数值随约束模态轴承刚度增加呈增大趋势。在高速齿轮轴系临界转速准确计算中,轴承刚度及陀螺效应影响不可忽视。Abstract: Due to the unbalance quantity factors ofa high-speed gear shafting system,its gyroscopic effect may generate a large bending moment and cause potentially dangerous resonance. The high-speed input shafting model of a certain type of coaxial high-speed helicopter′s transmission system was established with the beam element method and the finite element method respectively. The vortex phenomenon of the high-speed gear shafting system with different vibration modes was systematically studied. Combined with its critical speed Campbell diagram, the freedom iscompared with the constraint modal under different influences of bearing stiffness on the critical speed value. The results show that the torsion and expansion modes of the high-speed gear shafting system do not produce vortices in free and constrained modes, while the transverse modes such as bendingdiameter and pitch diameter generate significant vortices, which are weakened in the constrained mode. The value of critical speed increases with the increase of the bearing stiffness of constrained modal. The critical speed of the high-speed shafting system can be accurately calculated with the bearing stiffness and the gyroscopic effect considered.
-
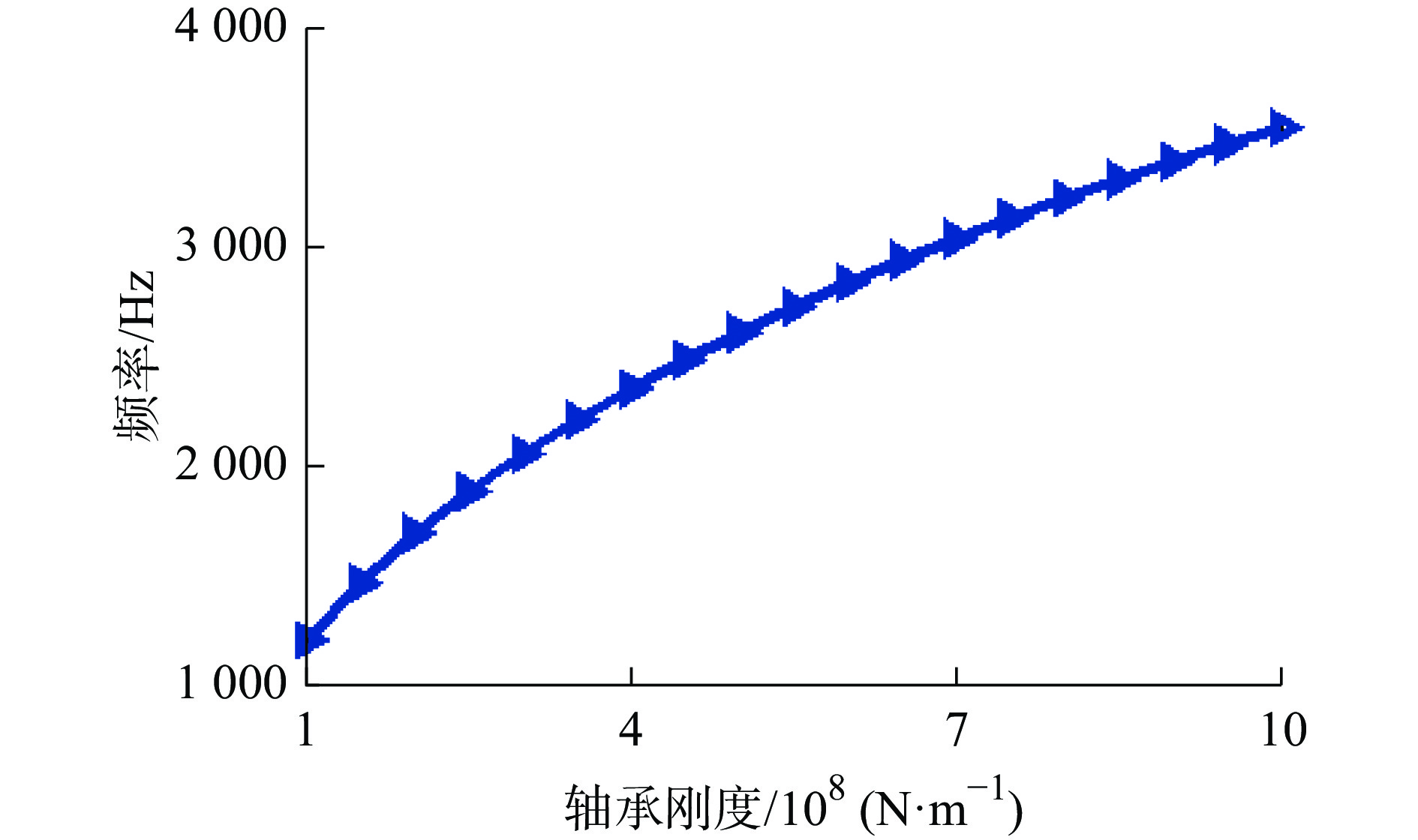
表 1 各工况下对应轴承刚度
工况 轴承 刚度/108(N·m−1) kxx kyy 地面慢车(0.5n) 1 1.28 5.61 2 1.18 4.89 起飞、着陆(1.0n) 1 1.71 6.53 2 1.27 5.28 悬停 (0.9n) 1 1.71 6.53 2 1.27 5.28 悬停 (1.0n) 1 1.56 5.18 2 1.21 5.00 正常前飞或侧飞(1.0n) 1 1.28 5.63 2 1.18 4.89 高速前飞或侧飞(0.85n) 1 2.19 7.58 2 2.53 6.29 单发飞行(1.0n) 1 1.61 6.3 2 1.22 5.09 表 2 高速齿轮轴齿轮参数
齿数 模数/
mm压力角/
(°)齿宽/
mm额定转速/
(r·min−1)啮频/
Hz25 3.2494 20 55 21600 9000 表 3 自由模态下频率结果
阶次 频率/Hz 临界转速/(r·min−1) 1 4098.8 245928 2 7363.0 441780 表 4 正常前飞或侧飞频率结果
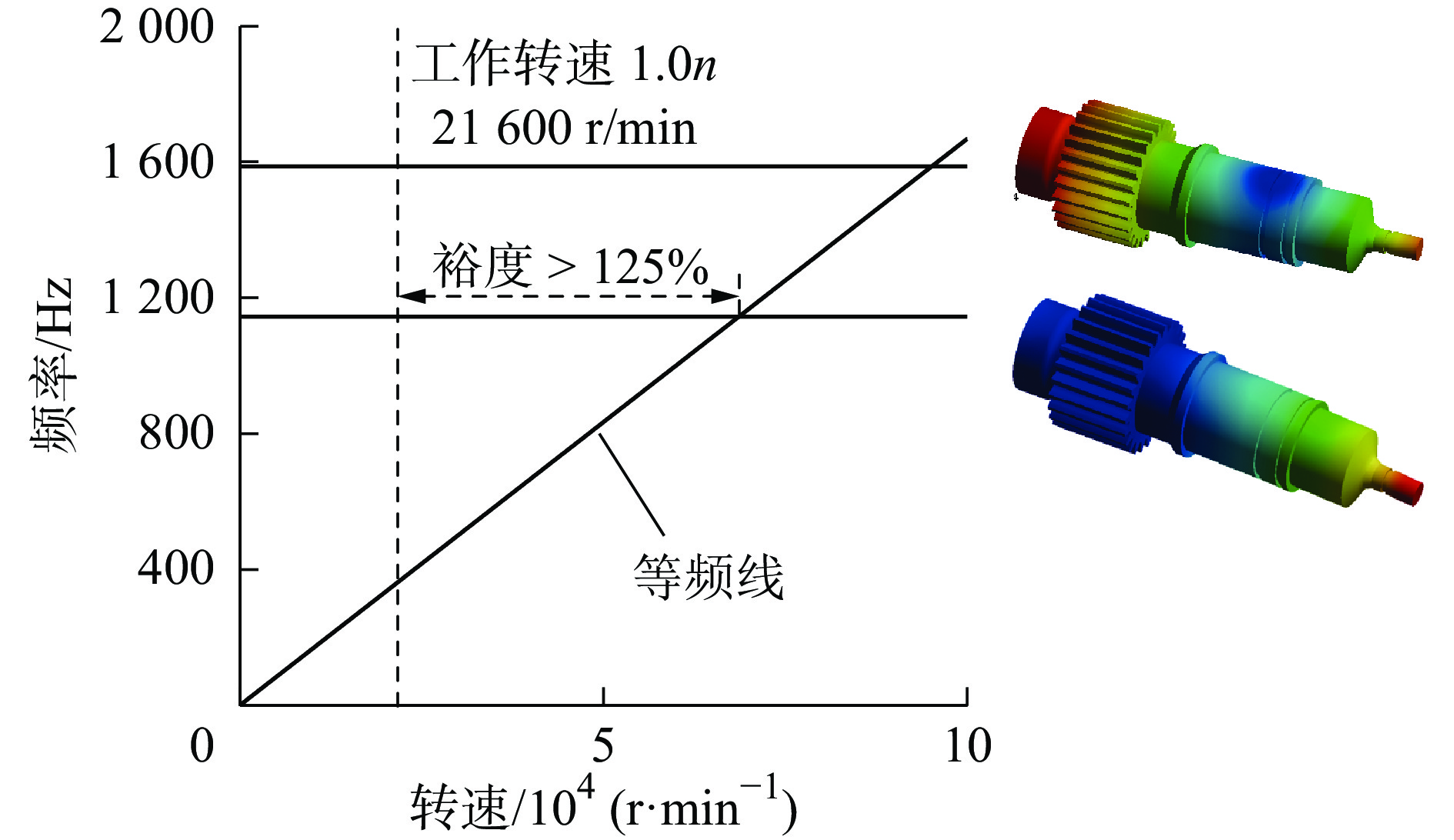
阶次 频率/Hz 临界转速/(r·min−1) 1 1143 68580 2 1587 95220 表 5 各工况下的临界转速
不同工况 阶次 频率/
Hz临界转速/
(r·min−1)安全裕度/
%地面慢车 1 1143 68580 535 起飞/着陆 1 1305 78300 262 悬停(0.9n) 1 1305 78300 302 悬停(1.0n) 1 1252 75120 247 正常前飞或侧飞 1 1143 68580 217 高速前飞或侧飞 1 1473 88380 381 单发飞行 1 1270 76200 252 -
[1] 隋永枫, 吕和祥. 陀螺效应对转子横向振动的影响分析[J]. 计算力学学报, 2003, 20(6): 711-714 doi: 10.3969/j.issn.1007-4708.2003.06.011SUI Y F, LYU H X. Influence of gyroscopic term to the vibration of rotor system[J]. Chinese Journal of Computational Mechanics, 2003, 20(6): 711-714 (in Chinese) doi: 10.3969/j.issn.1007-4708.2003.06.011 [2] 瓮雷, 杨自春, 曹跃云. 转子系统临界转速计算及不平衡响应分析[J]. 四川兵工学报, 2012, 33(11): 65-69 + 72WENG L, YANG Z C, CAO Y Y. Critical speed calculation and unbalance response analysis of rotor system[J]. Journal of Ordnance Equipment Engineering, 2012, 33(11): 65-69 + 72 (in Chinese) [3] 王永亮, 孙立权, 崔颖, 等. 考虑陀螺效应的转子动力学相似准则[J]. 航空动力学报, 2015, 30(12): 2840-2847WANG Y L, SUN L Q, CUI Y, et al. Dynamics similarity criteria of rotor dynamic with gyroscopic effect[J]. Journal of Aerospace Power, 2015, 30(12): 2840-2847 (in Chinese) [4] 陈金, 金栋平, 刘福寿. 论分布式陀螺柔性体结构的动力学建模问题[J]. 振动工程学报, 2020, 33(1): 74-81CHEN J, JIN D P, LIU F S. On dynamic modeling of distributed gyros flexible structures[J]. Journal of Vibration Engineering, 2020, 33(1): 74-81 (in Chinese) [5] 钱新, 杜星文. 旋转Rayleigh梁动力学性能的研究[J]. 力学学报, 2011, 43(3): 635-640 doi: 10.6052/0459-1879-2011-3-lxxb2009-712QIAN X, DU X W. Dynamic characteristics of spinning Rayleigh beams[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(3): 635-640 (in Chinese) doi: 10.6052/0459-1879-2011-3-lxxb2009-712 [6] 周健斌, 章俊杰, 孟光. 计及陀螺效应的翼吊式机翼-发动机系统结构动力学特性研究[J]. 振动与冲击, 2012, 31(6): 145-149 doi: 10.3969/j.issn.1000-3835.2012.06.030ZHOU J B, ZHANG J J, MENG G. Structural dynamic characteristics of a wing-engine system with gyro effects[J]. Journal of Vibration and Shock, 2012, 31(6): 145-149 (in Chinese) doi: 10.3969/j.issn.1000-3835.2012.06.030 [7] VAN LOAN C. A Symplectic method for approximating all the eigenvalues of a Hamiltonian matrix[J]. Linear Algebra and Its Applications, 1984, 61: 233-251 doi: 10.1016/0024-3795(84)90034-X [8] 钟万勰. 应用力学对偶体系[M]. 北京: 科学出版社, 2002ZHONG W X. Dual system of applied mechanics[M]. Beijing: Science Press, 2002 (in Chinese) [9] 刘伟佳. 陀螺效应对转子临界转速的影响[J]. 吉林师范大学学报(自然科学版), 2012, 33(3): 47-49LIU W J. Impact of gyroscopic effect on the critical speed of the rotor[J]. Journal of Jilin Normal University (Natural Science Edition), 2012, 33(3): 47-49 (in Chinese) [10] 倪德, 李科锋, 刘建武. 基于分布质量轴模型的尾传动轴系临界转速分析[J]. 南京航空航天大学学报, 2016, 48(6): 822-827NI D, LI K F, LIU J W. Critical speed analysis of helicopter tail drive shaft based on distributed mass shaft model[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2016, 48(6): 822-827 (in Chinese) [11] DE FELICE A, SORRENTINO S. Damping and gyroscopic effects on the stability of parametrically excited continuous rotor systems[J]. Nonlinear Dynamics, 2021, 103(4): 3529-3555 doi: 10.1007/s11071-020-06106-3 [12] 胡腾, 殷国富, 孙明楠. 基于离心力和陀螺力矩效应的“主轴-轴承”系统动力学特性研究[J]. 振动与冲击, 2014, 33(8): 100-108HU T, YIN G F, SUN M N. Dynamic performance of a shaft-bearing system with centrifugal force and gyroscopic moment effects[J]. Journal of Vibration and Shock, 2014, 33(8): 100-108 (in Chinese) [13] JAHANGIRI M, ASGHARI M, BAGHERI E. Torsional vibration induced by gyroscopic effect in the modified couple stress based micro-rotors[J]. European Journal of Mechanics-A/Solids, 2020, 81: 103907 doi: 10.1016/j.euromechsol.2019.103907 [14] 成永博, 卢永刚, 黎启胜, 等. 陀螺效应对精密离心机加速度的影响研究[J]. 机械科学与技术, 2013, 32(6): 801-804CHENG Y B, LU Y G, LI Q S, et al. The influence of gyroscopic effect on acceleration of precision centrifuge[J]. Mechanical Science and Technology for Aerospace Engineering, 2013, 32(6): 801-804 (in Chinese) [15] ZASTEMPOWSKI M, BOCHAT A. Gyroscopic effect in machine working assemblies[J]. Acta Technologica Agriculturae, 2020, 23(1): 24-29 doi: 10.2478/ata-2020-0005 [16] SEDDIGHI H, EIPAKCHI H. Natural frequency and critical speed determination of an axially moving viscoelastic beam[J]. Mechanics of Time-Dependent Materials, 2013, 17(4): 529-541 doi: 10.1007/s11043-012-9201-1 [17] DANESHJOU K, TALEBITOOTI M, TALEBITOOTI R. Free vibration and critical speed of moderately thick rotating laminated composite conical shell using generalized differential quadrature method[J]. Applied Mathematics and Mechanics, 2013, 34(4): 437-456 doi: 10.1007/s10483-013-1682-8 [18] 张爱强. 非惯性系下直升机主减速器高精度动力学建模及动态行为机理研究[D]. 重庆: 重庆大学, 2020ZHANG A Q. High-accuracy dynamics modeling and dynamic behavior mechanism of helicopter main reducer in non-inertial system[D]. Chongqing: Chongqing University, 2020 (in Chinese) -







 下载:
下载: