Application of Improved Whale Optimization Algorithm in Time-optimal Trajectory Planning of Manipulator
-
摘要: 针对机械臂时间最优轨迹规划问题,提出一种改进鲸鱼优化算法的最优轨迹规划方法。首先把机械臂各个关节的角度、角速度、角加速度作为约束参数,在关节空间中采用五次多项式插值构造机械臂的轨迹,然后建立以机械臂运行时间最优为目标的目标函数,采用改进的鲸鱼优化算法(IWOA)来对时间进行优化,提高机械臂的运行效率。最后通过MATLAB进行仿真,结果表明,改进的鲸鱼优化算法相较于其它同类算法求解精度更高,收敛速度更快,并且经过IWOA和轨迹优化结合得到的机械臂的位移、速度和加速度曲线都是平滑的且没有明显的突变,验证了该轨迹规划方法的有效性。Abstract: An optimal trajectory planning method based on improved whale optimization algorithm is proposed in order to solve the time optimal trajectory planning problem of manipulator. Firstly, the trajectory of the manipulator is constructed by quintic polynomial interpolation in the joint space with the constrains in the kinematic limits of velocity, acceleration, and jerk. Then, the objective function is established to minimize the running time of the manipulator and the improved whale optimization algorithm (IWOA) is used to optimize the time to improve the operation efficiency of the manipulator. Finally, the MATLAB simulation results show that the improved whale optimization algorithm has higher solvingaccuracy and faster convergence speed than other similar algorithms, and the displacement, velocity and acceleration curves of the manipulator which were obtained by combining IWOA and trajectory optimization are smooth without obvious mutation, which verifies the effectiveness of the proposed trajectory planning method.
-
Key words:
- manipulator /
- time-optimal trajectory planning /
- IWOA /
- quintic polynomial
-
表 1 4种算法实验参数设置
算法 参数 WOA – IWOA 种群规模为30;最大迭代次数为500;
空间维度为30;k = 0.4GWO a=[2,0] PSO wmax=0.9,wmin=0.4,c1=c2=2.0 表 2 6个基准测试函数
函数表达式 维数 定义域 理论最优值 $ {f_1}(x) = \displaystyle\sum\limits_{i = 1}^d {x_i^2} $ 30 $ [ - 100,100] $ 0 $ {f_2}(x) = \displaystyle\sum\limits_{i = 1}^d {\left| {{x_i}} \right|} + \prod _{i = 1}^d\left| {{x_i}} \right| $ 30 $ [ - 10,10] $ 0 $ {f_3}(x) = \displaystyle\sum\limits_{i = 1}^d {[100(} {x_{i + 1}} - x_i^2{)^2} - {({x_i} - 1)^2}] $ 30 $ [ - 10,10] $ 0 $\begin{gathered} {f_4}(x) = - 20\exp \left( { - 0.2\sqrt {\dfrac{1}{d}\displaystyle\sum\limits_{i = 1}^d {x_i^2} } } \right) - \exp \left( {\dfrac{1}{d}\displaystyle\sum\limits_{i = 1}^d {\cos (2\text{π} {x_i})} } \right) + 20 + e \\ \end{gathered}$ 30 $ [ - 32,32] $ 0 ${f_5}(x) = \dfrac{1}{ {4\;000} }\displaystyle\sum\limits_{i = 1}^d {x_i^2 - \prod\limits_{i = 1}^d {\cos \left(\dfrac{ { {x_i} } }{ {\sqrt i } }\right)} } + 1$ 30 $ [ - 600,600] $ 0 ${f_6}(x) = x_i^2 - 10\cos (2\text{π} {x_i}) + 10$ 30 $ [ - 5.12,5.12] $ 0 表 3 基准测试函数优化结果
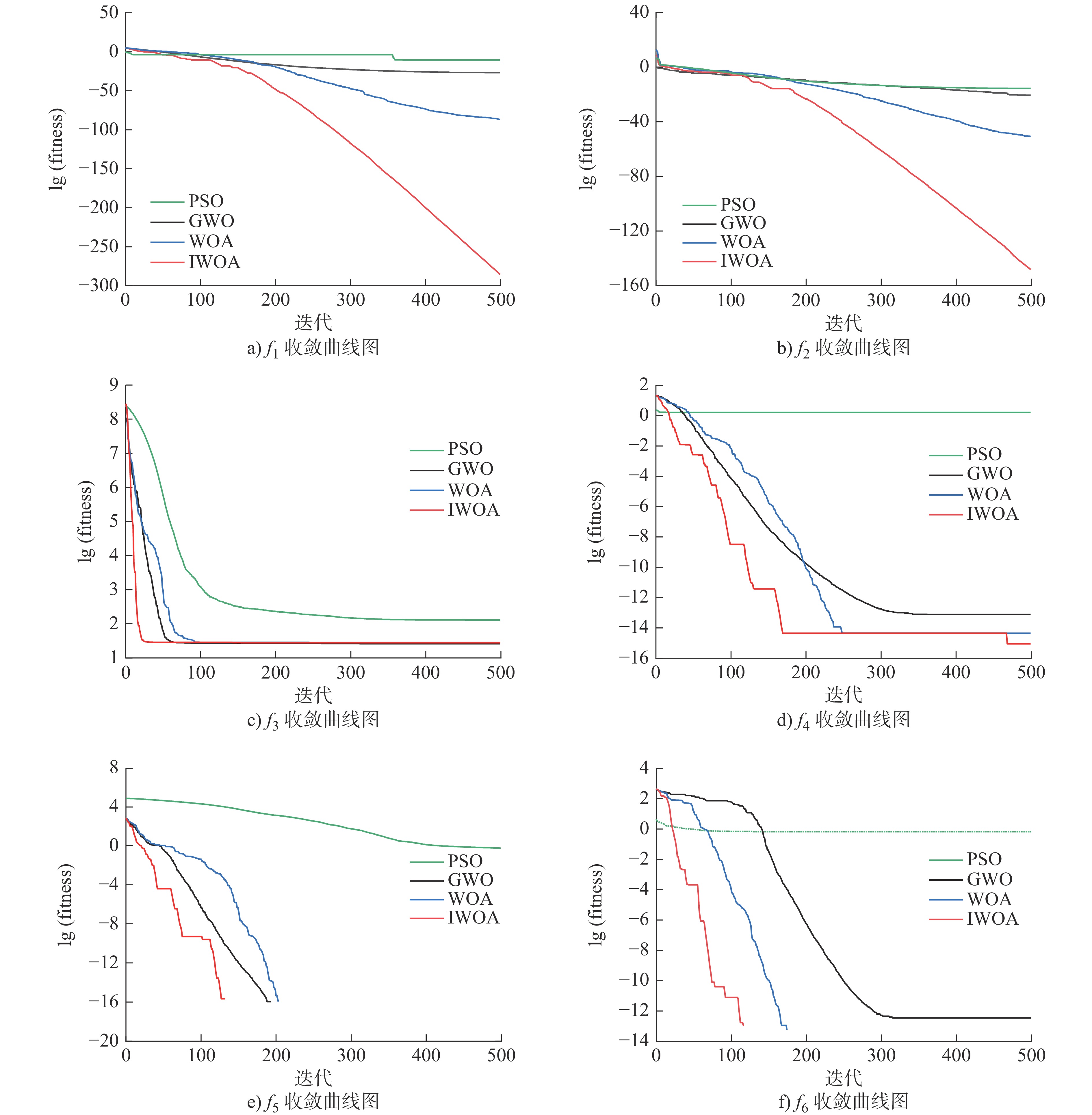
指标 算法 f1 f2 f3 f4 f5 f6 Best WOA 2.58×10−87 6.52×10−58 2.78×101 4.44×10−15 0.00×100 0.00×100 IWOA 2.94×10−289 1.59×10−149 2.41×101 8.88×10−16 0.00×100 0.00×100 GWO 6.21×10−29 2.38×10−17 2.58×101 6.84×10−14 0.00×100 5.68×10−14 PSO 7.56×10−5 8.89×10−1 2.21×101 1.80×10−3 2.61×10−5 1.23×102 Mean WOA 2.56×10−80 4.32×10−53 2.80×101 6.31×10−15 0.00×100 2.84×10−15 IWOA 4.01×10−282 2.12×10−145 2.47×101 8.88×10−16 0.00×100 0.00×100 GWO 1.01×10−27 4.03×10−17 2.71×101 1.21×10−13 3.93×10−3 2.32×102 PSO 4.12×10−4 4.15×101 1.99×102 6.36×100 3.15×10−1 3.58×102 Worst WOA 2.26×10−74 1.04×10−50 2.88×101 8.88×10−15 0.00×100 5.68×10−14 IWOA 8.44×10−280 1.37×10−141 2.49×101 8.88×10−16 0.00×100 0.00×100 GWO 3.85×10−27 2.72×10−16 2.79×101 1.36×10−13 3.26×10−2 5.68×102 PSO 3.12×10−2 2.24×102 5.21×102 1.21×101 5.93×10−1 1.05×102 Std. WOA 4.04×10−80 9.12×10−59 2.34×101 4.89×10−16 0.00×100 8.07×10−15 IWOA 3.32×10−283 3.12×10−146 1.56×101 4.56×10−17 0.00×100 0.00×100 GWO 1.36×10−28 3.57×10−18 7.08×10−1 1.72×10−14 8.13×10−2 3.78×102 PSO 5.26×10−4 6.36×101 4.32×101 7.42×100 4.09×10−1 4.32×102 表 4 路径点序列
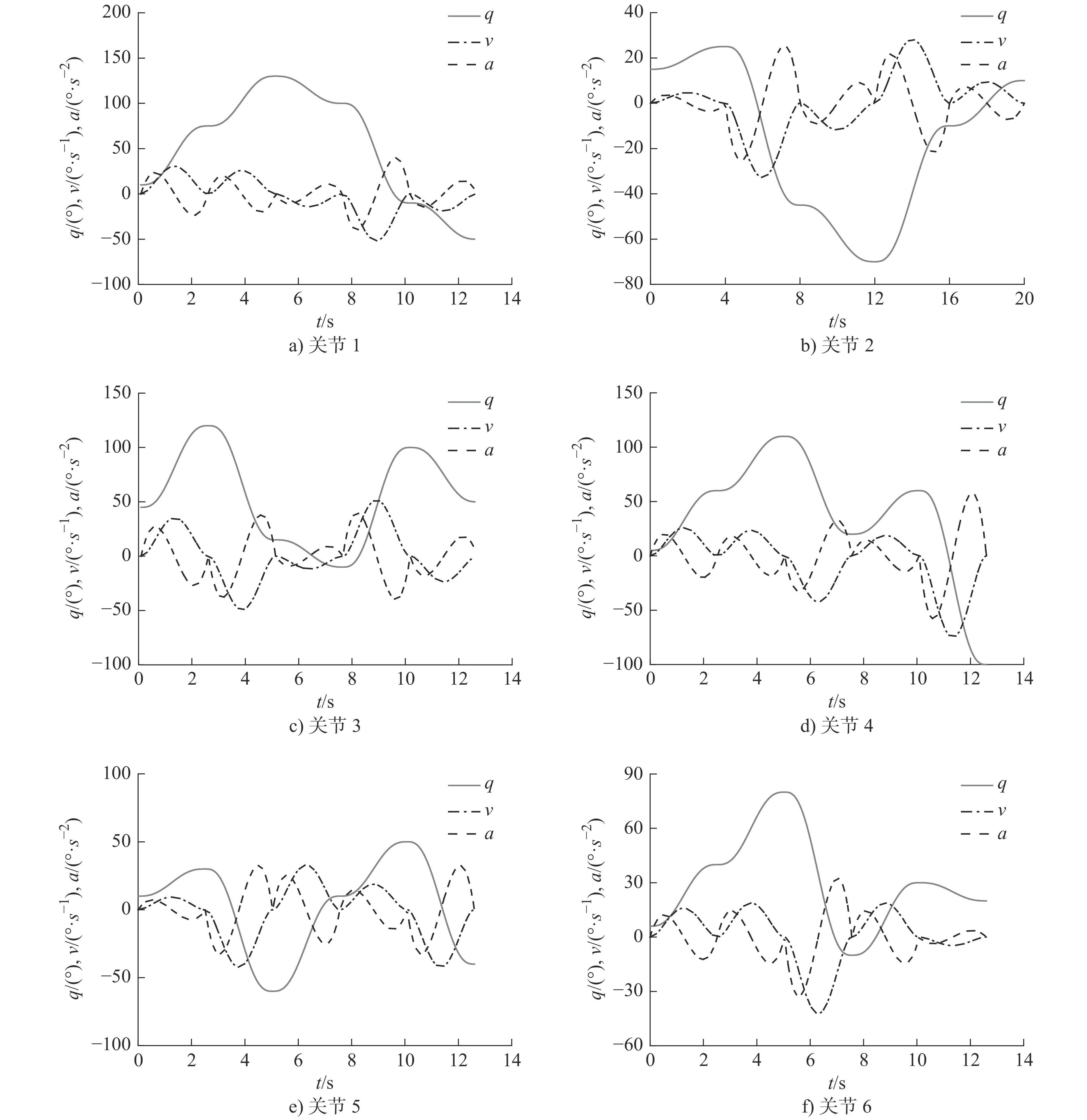
路径点 关节1/(°) 关节2/(°) 关节3/(°) 关节4/(°) 关节5/(°) 关节6/(°) 1 10 15 45 5 10 6 2 75 25 120 60 30 40 3 130 −45 15 110 −60 80 4 100 −70 −10 20 10 −10 5 −10 −10 100 60 50 30 6 −50 10 50 −100 −40 20 表 5 机械臂关节约束条件
关节 速度/(°·s−1 ) 加速度/(°·s−2) 加加速度/(°·s−3 ) 1 100 45 60 2 95 40 60 3 100 75 55 4 150 70 70 5 130 90 75 6 110 80 70 -
[1] 侯庆隆, 杨冬, 郭士杰. 工业机器人能耗优化方法研究综述[J]. 计算机工程与应用, 2018, 54(22): 1-9. doi: 10.3778/j.issn.1002-8331.1809-0021HOU Q L, YANG D, GUO S J. Review on energy consumption optimization methods of industrial robots[J]. Computer Engineering and Applications, 2018, 54(22): 1-9. (in Chinese) doi: 10.3778/j.issn.1002-8331.1809-0021 [2] GASPARETTO A, ZANOTTO V. Optimal trajectory planning for industrial robots[J]. Advances in Engineering Software, 2010, 41(4): 548-556. doi: 10.1016/j.advengsoft.2009.11.001 [3] 康代轲, 陈明. 基于改进混沌搜索算法的机器人轨迹规划[J]. 计算机工程与应用, 2017, 53(14): 143-147. doi: 10.3778/j.issn.1002-8331.1607-0132KANG D K, CHEN M. Planning and simulation of robot optimal trajectory based on improved chaotic search algorithm[J]. Computer Engineering and Applications, 2017, 53(14): 143-147. (in Chinese) doi: 10.3778/j.issn.1002-8331.1607-0132 [4] NAGY Á, VAJK I. Nonconvex time-optimal trajectory planning for robot manipulators[J]. Journal of Dynamic Systems, Measurement, and Control, 2019, 141(11): 111007. doi: 10.1115/1.4044216 [5] 欧新, 周璐, 张鸷, 等. 电能表检验台体串联机械臂时间最优轨迹规划[J]. 计算机工程与应用, 2022, 58(6): 250-255. doi: 10.3778/j.issn.1002-8331.2009-0455OU X, ZHOU L, ZHANG Z, et al. Time optimal trajectory planning for tandem manipulator of electric energy meter test platform[J]. Computer Engineering and Applications, 2022, 58(6): 250-255. (in Chinese) doi: 10.3778/j.issn.1002-8331.2009-0455 [6] 王学琨, 李刚, 周东凯, 等. 基于DE的时间最优6-DOF机械臂轨迹规划算法[J]. 计算机仿真, 2015, 32(8): 332-337. doi: 10.3969/j.issn.1006-9348.2015.08.072WANG X K, LI G, ZHOU D K, et al. Time-optimal trajectory planning algorithm based on DE for manipulator[J]. Computer Simulation, 2015, 32(8): 332-337. (in Chinese) doi: 10.3969/j.issn.1006-9348.2015.08.072 [7] XIDIAS E K. Time-optimal trajectory planning for hyper-redundant manipulators in 3D workspaces[J]. Robotics and Computer-Integrated Manufacturing, 2018, 50: 286-298. doi: 10.1016/j.rcim.2017.10.005 [8] 晋文科, 张华, 刘满禄. 基于NURBS算法的冗余机械臂轨迹规划[J]. 科学技术与工程, 2014, 14(28): 226-230. doi: 10.3969/j.issn.1671-1815.2014.28.044JIN W K, ZHANG H, LIU M L. Trajectory planning of redundant manipulator based on NURBS[J]. Science Technology and Engineering, 2014, 14(28): 226-230. (in Chinese) doi: 10.3969/j.issn.1671-1815.2014.28.044 [9] 于瑞, 王成军, 郭永存, 等. 基于杂交算法的机器人时间最优轨迹规划[J]. 机械传动, 2018, 42(7): 55-60.YU R, WANG C J, GUO Y C, et al. Time-optimal trajectory planning of robot based on breed algorithm[J]. Journal of Mechanical Transmission, 2018, 42(7): 55-60. (in Chinese) [10] 王延年, 向秋丽. 基于改进粒子群优化算法的六自由度机器人轨迹优化[J]. 国外电子测量技术, 2020, 39(1): 49-53.WANG Y N, XIANG Q L. Trajectory of 6-DOF robot based on improved particle swarm optimization algorithm[J]. Foreign Electronic Measurement Technology, 2020, 39(1): 49-53. (in Chinese) [11] MA J W, GAO S, YAN H T, et al. A new approach to time-optimal trajectory planning with torque and jerk limits for robot[J]. Robotics and Autonomous Systems, 2021, 140: 103744. doi: 10.1016/j.robot.2021.103744 [12] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67. doi: 10.1016/j.advengsoft.2016.01.008 [13] MIRJALILI S, GANDOMI A H. Chaotic gravitational constants for the gravitational search algorithm[J]. Applied Soft Computing, 2017, 53: 407-419. doi: 10.1016/j.asoc.2017.01.008 [14] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. doi: 10.1016/j.advengsoft.2013.12.007 [15] KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of International Conference on Neural Networks. Perth: IEEE, 1995: 1942-1948 -








 下载:
下载: