Application of Parameterized Level Set Method to Multi-objective Topology Optimization of Orthotropic Structures
-
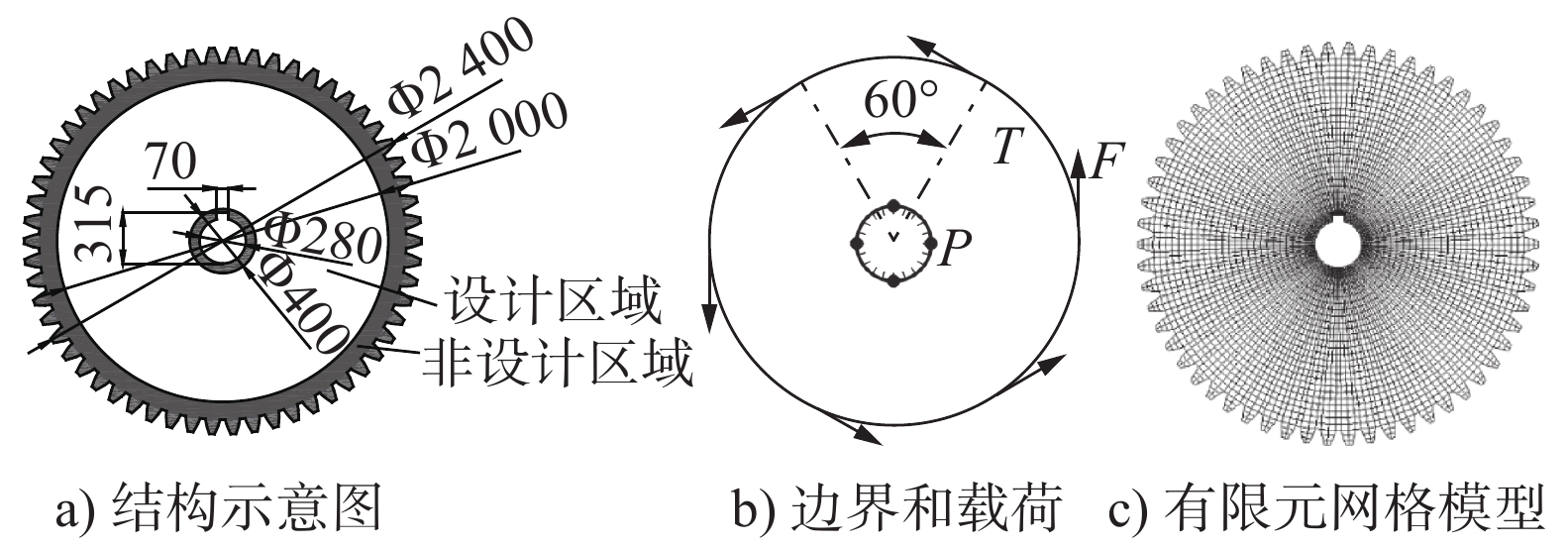
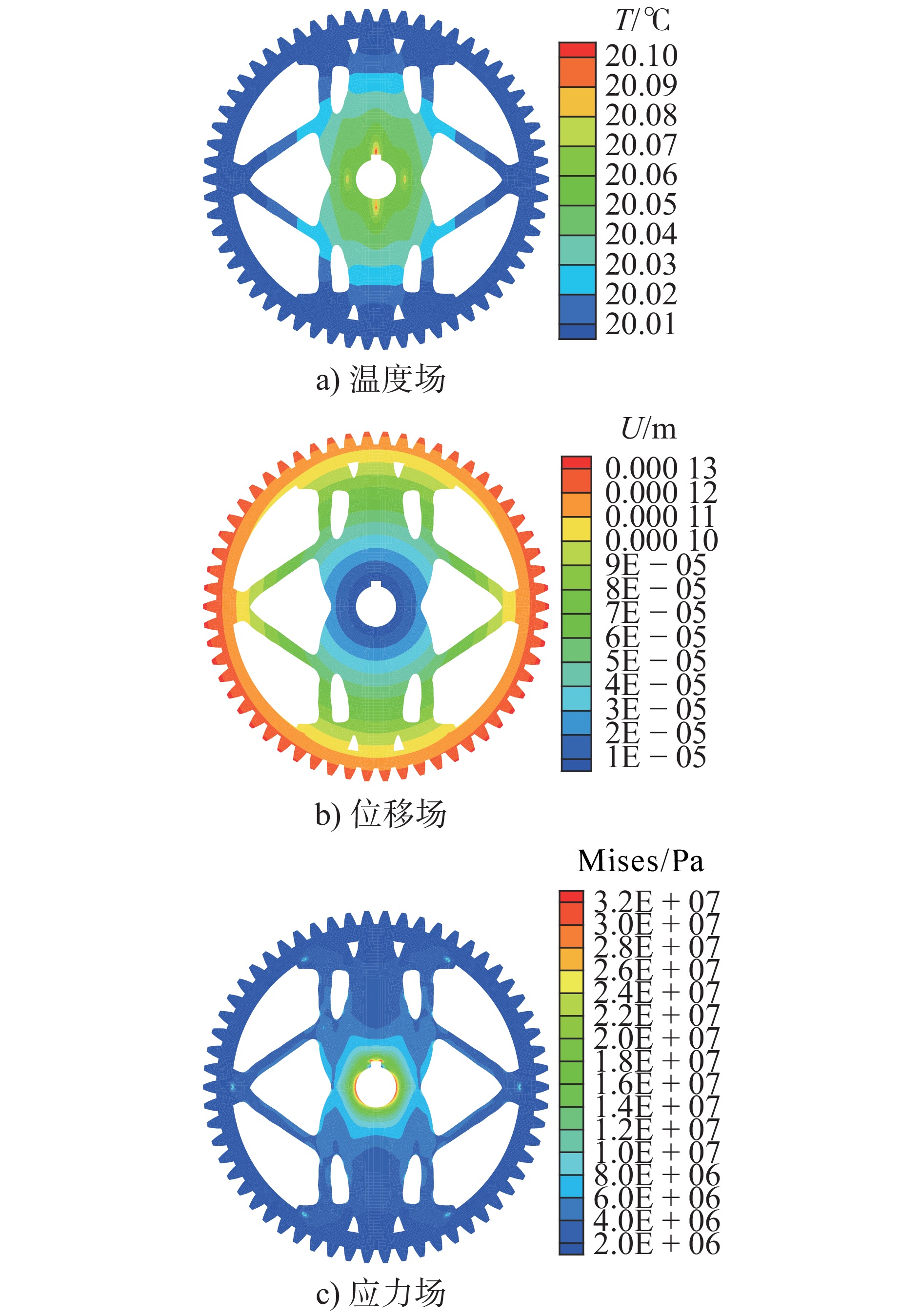
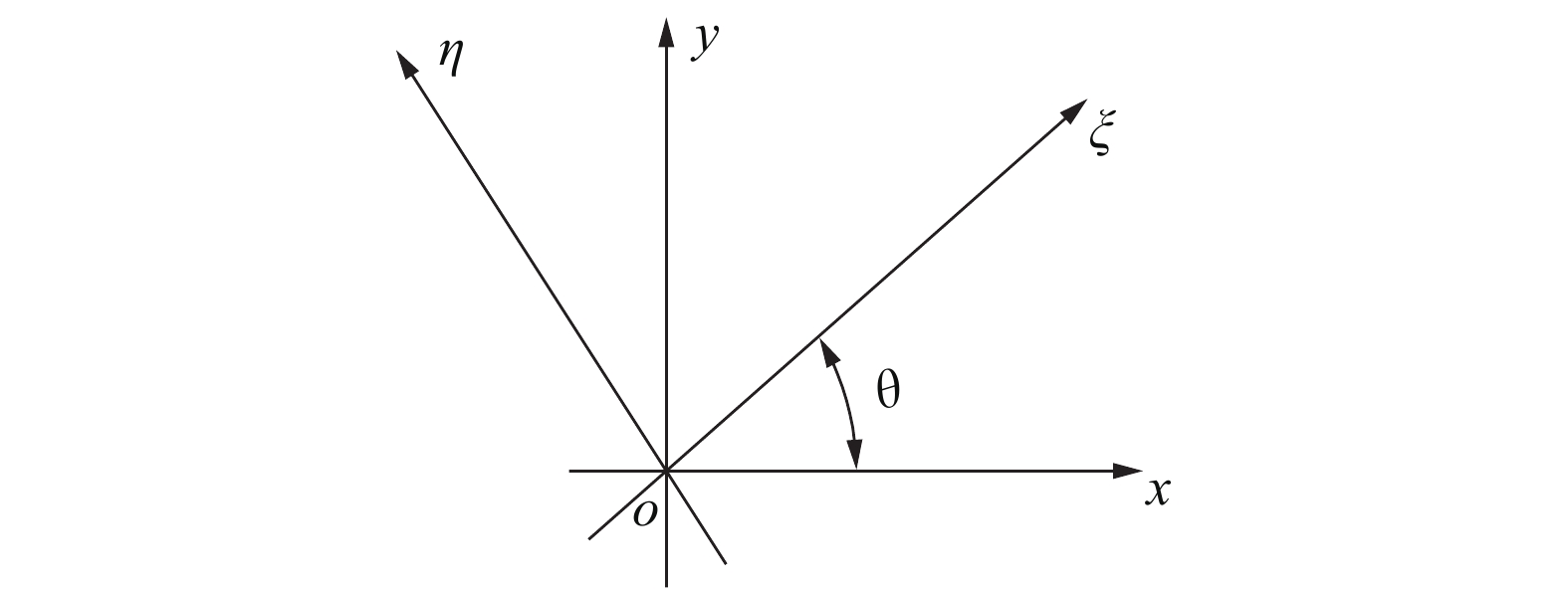
摘要: 利用全局支撑径向基函数插值初始水平集函数，以水平集函数为设计变量，以结构柔度和散热弱度的加权函数为目标函数，基于参数化水平集法（Parameterized level set method，PLSM）建立了正交各向异性结构的热力耦合多目标拓扑优化模型。结合数值算例研究了权系数、材料方向角、泊松比因子和热导率因子对PLSM多目标最优拓扑结构和目标函数的影响，并给出了相关参数的合理取值范围；在3D打印实物的基础上完成了最优各向异性拓扑结构的性能分析，并与各向同性结构进行了对比讨论。结果表明，PLSM最优拓扑结构比变密度法的拓扑结构边界更光滑、清晰，不会出现中间密度和锯齿等现象；同时正交各向异性结构的温度场、位移场和应力场比各向同性结构均有较好地改善，加权目标函数、结构柔度和散热弱度分别降低了55%、3.18%和81.1%。Abstract: the initial level set function was interpolated by using the radial basis functions with global supports, and the level set functions and weighted function of compliance and heat dissipation were chosen as the design variables and objective function, respectively; and then the thermo-mechanical coupling multi-objective topology optimization model for the orthotropic structure was established based on the parameterized level set method (PLSM). The influence of weight coefficient, off-angle, Poisson's ratio factor and thermal conductivity factor on the multi-objective optimal topological structure and objective function value was studied through numerical examples, and the reasonable range of the above parameters was provided. The performance analysis of the optimal orthotropic topological structure was performed on the basis of 3D printed products, which was compared with that of the isotropic structure. The results show that the profile of PLSM optimal topological structure is smoother and clearer than that of the topological structure based on the variable density method, and there will be no intermediate density and sawtooth. The temperature, displacement and stress field of the orthotropic structure are improved compared with the isotropic structure, and the weighted objective function, compliance and heat dissipation are reduced by 55%, 3.18% and 81.1%, respectively.
-
图 3 不同材料方向角下最优拓扑结构和加权目标函数值（
$w{\text{ = }}0.5$ 、$Bt{\text{ = }}0.65$ 、$Ht{\text{ = 0}}{\text{.5}}$ ）
图 4 不同泊松比因子下最优拓扑结构和加权目标函数值（
$w{\text{ = }}0.5$ 、$Ht{\text{ = 0.5}}$ 、$\theta {\text{ = }}{0}$ ）
图 5 不同热导率因子下最优拓扑结构和加权目标函数值（
$w{\text{ = }}0.5$ 、$Bt{\text{ = }}0.65$ 、$\theta {\text{ = }}{0 }$ ）
图 7 各向异性齿轮最优拓扑结构的温度场、位移场和应力场（
$w{\text{ = }}0.5$ 、$\theta {\text{ = }}{0 }$ 、$Bt{\text{ = }}0.65$ 、$Ht{\text{ = 0}}{\text{.1}}$ ）
图 8 各向同性齿轮最优拓扑结构的温度场、位移场和应力场（
$w{\text{ = }}0.5$ 、$\theta {\text{ = }}{0 }$ 、$Bt{\text{ = }}0.65$ 、$Ht{\text{ = 0}}{\text{.1}}$ ）表 1 权系数和正交各向异性参数的取值
序号 权系数$w $ 材料方向角θ/（°） 泊松比因子Bt 热导率因子Ht 1 0、0.1、0.3、0.5、0.7、0.9、1 0 0.65 0.5 2 0.5 0、15、30、45、60、75 0.65 0.5 3 0.5 0 0.65、0.75、0.85、2、3、4 0.5 4 0.5 0 0.65 0.10、0.25、0.50、2、4、10 
下载: 导出CSV
表 2 不同权系数
$w$ 下的最优拓扑结构 （$\theta {\text{ = }}{0 }$ 、$Bt{\text{ = }}0.65$ 、$Ht{\text{ = 0}}{\text{.5}}$ ）$w{\text{ = }}0$ $w{\text{ = }}0.1$ $w{\text{ = }}0.3$ $w{\text{ = }}0.5$ $w{\text{ = }}0.7$ $w{\text{ = }}0.9$ $w{\text{ = 1}}$ PLSM最优
拓扑结构
SIMP密度
云图
3D打印
模型
下载: 导出CSV
表 3 权系数对齿轮加权目标函数、柔度和散热弱度的影响（
$\theta {\text{ = }}{0 }$ 、$Bt{\text{ = }}0.65$ 、$Ht{\text{ = 0}}{\text{.5}}$ ）w 0.1 0.3 0.5 0.7 0.9 加权目标函数 0.24 0.28 0.27 0.26 0.25 柔度/Nm 163.06 156.59 137.94 131.65 129.66 散热弱度/W 13.82 14.07 14.95 16.59 18.10
下载: 导出CSV
表 4 材料方向角对齿轮加权目标函数、柔度和散热弱度的影响 （
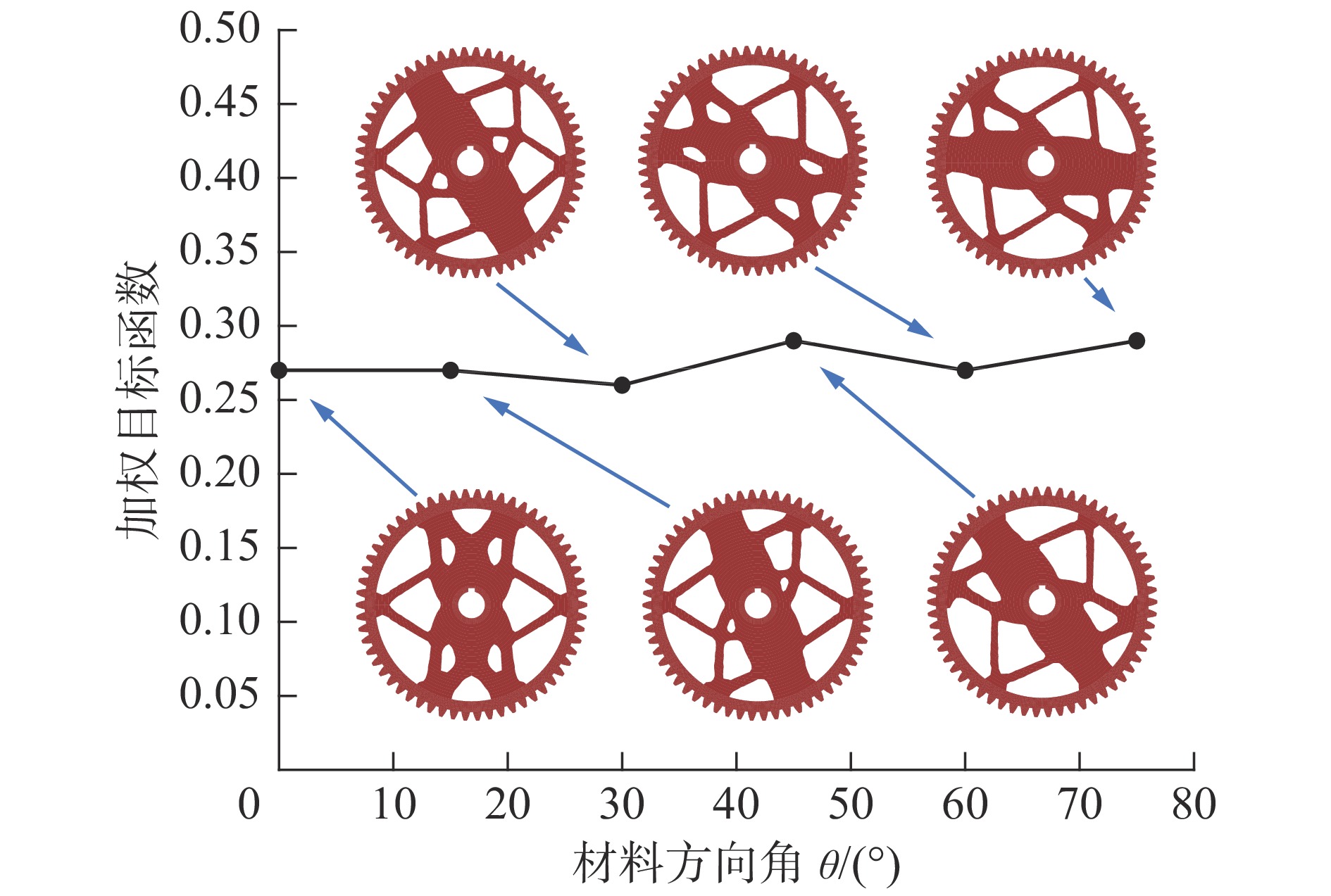
$w{\text{ = }}0.5$ 、$Bt{\text{ = }}0.65$ 、$Ht{\text{ = 0}}{\text{.5}}$ ）θ/（°） 0 15 30 45 60 75 加权目标函数 0.27 0.27 0.26 0.29 0.27 0.29 柔度/Nm 137.94 138.22 136.09 143.56 138.70 144.57 散热弱度/W 14.95 14.84 15.03 14.81 14.77 14.87
下载: 导出CSV
表 5 泊松比因子对齿轮加权目标函数、柔度和散热弱度的影响 （
$w{\text{ = }}0.5$ 、$Ht{\text{ = 0}}{\text{.5}}$ 、$\theta {\text{ = }}{0 }$ ）Bt 0.65 0.75 0.85 2 3 4 加权目标函数 0.27 0.28 0.30 0.43 0.50 0.60 柔度/Nm 137.94 142.32 145.78 179.57 199.80 225.82 散热弱度/W 14.95 15.04 15.17 16.43 16.79 17.29
下载: 导出CSV
表 6 热导率因子对齿轮加权目标函数、柔度和散热弱度的影响 （
$w{\text{ = }}0.5$ 、$Bt{\text{ = }}0.65$ 、$\theta {\text{ = }}{0}$ ）Ht 0.10 0.25 0.50 2 4 10 加权目标函数 0.18 0.22 0.27 0.43 0.51 0.62 柔度/Nm 144.77 142.23 137.94 140.45 144.68 153.30 散热弱度/W 4.39 9.15 14.95 29.51 34.89 42.61
下载: 导出CSV
表 7 各向异性/各向同性齿轮的加权目标函数、柔度和散热弱度对比
齿轮 加权目标函数 柔度/Nm 散热弱度/W 各向异性 0.18 144.77 4.39 各向同性 0.40 149.52 23.23
下载: 导出CSV
-
[1] SETIAWAN N B, ZIMMERMAN R W. A unified methodology for computing the stresses around an arbitrarily-shaped hole in isotropic or anisotropic materials[J]. International Journal of Solids and Structures, 2020, 199: 131-143. doi: 10.1016/j.ijsolstr.2020.03.022 [2] BERIHA B, SAHOO U C. Analysis of flexible pavement with cross-anisotropic material properties[J]. International Journal of Pavement Research and Technology, 2020, 13(4): 411-416. doi: 10.1007/s42947-020-0284-9 [3] KIM D, LEE J, NOMURA T, et al. Topology optimization of functionally graded anisotropic composite structures using homogenization design method[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 369: 113220. doi: 10.1016/j.cma.2020.113220 [4] KAZEMI H, NORATO J A. Topology optimization of lattices with anisotropic struts[J]. Structural and Multidisciplinary Optimization, 2021, 63(4): 1653-1668. doi: 10.1007/s00158-020-02822-x [5] ZHANG J P, WANG S S, ZHOU G Q, et al. Topology optimization of thermal structure for isotropic and anisotropic materials using the element-free Galerkin method[J]. Engineering Optimization, 2020, 52(7): 1097-1118. doi: 10.1080/0305215X.2019.1636979 [6] ZHANG W H, YANG J G, XU Y J, et al. Topology optimization of thermoelastic structures: mean compliance minimization or elastic strain energy minimization[J]. Structural and Multidisciplinary Optimization, 2014, 49(3): 417-429. doi: 10.1007/s00158-013-0991-9 [7] ZHU X F, ZHAO C, WANG X, et al. Temperature-constrained topology optimization of thermo-mechanical coupled problems[J]. Engineering Optimization, 2019, 51(10): 1687-1709. doi: 10.1080/0305215X.2018.1554065 [8] MENG Q X, XU B, WANG C, et al. Stress constrained thermo-elastic topology optimization based on stabilizing control schemes[J]. Journal of Thermal Stresses, 2020, 43(8): 1040-1068. doi: 10.1080/01495739.2020.1766391 [9] LI H, LI H, XIAO M, et al. Robust topology optimization of thermoelastic metamaterials considering hybrid uncertainties of material property[J]. Composite Structures, 2020, 248: 112477. doi: 10.1016/j.compstruct.2020.112477 [10] 占金青, 龙良明, 刘敏. 热弹性结构全局应力约束拓扑优化设计[J]. 机械科学与技术, 2019, 38(9): 1386-1392. doi: 10.13433/j.cnki.1003-8728.20190005ZHAN J Q, LONG L M, LIU M. Topology optimization of thermoelastic structures with global stress constraints[J]. Mechanical Science and Technology for Aerospace Engineering, 2019, 38(9): 1386-1392. (in Chinese) doi: 10.13433/j.cnki.1003-8728.20190005 [11] WEI P, LI Z Y, LI X P, et al. An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions[J]. Structural and Multidisciplinary Optimization, 2018, 58(2): 831-849. doi: 10.1007/s00158-018-1904-8 [12] WEI P, LIU Y, LI Z Y. A multi-discretization scheme for topology optimization based on the parameterized level set method[J]. International Journal for Simulation and Multidisciplinary Design Optimization, 2020, 11: 3. doi: 10.1051/smdo/2019019 [13] LIU Y, LI Z Y, WEI P, et al. Parameterized level-set based topology optimization method considering symmetry and pattern repetition constraints[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 340: 1079-1101. doi: 10.1016/j.cma.2018.04.034 [14] JIANG Y T, ZHAO M. Topology optimization under design-dependent loads with the parameterized level-set method based on radial-basis functions[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 369: 113235. doi: 10.1016/j.cma.2020.113235 [15] CUI M T, LUO C C, LI G, et al. The parameterized level set method for structural topology optimization with shape sensitivity constraint factor[J]. Engineering with Computers, 2021, 37(2): 855-872. doi: 10.1007/s00366-019-00860-8 [16] WANG L, LI Z S, NI B W, et al. Non-probabilistic reliability-based topology optimization (NRBTO) scheme for continuum structures based on the parameterized level-set method and interval mathematics[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 373: 113477. doi: 10.1016/j.cma.2020.113477 [17] LIU H, TIAN Y, ZONG H M, et al. Fully parallel level set method for large-scale structural topology optimization[J]. Computers & Structures, 2019, 221: 13-27. [18] CHU S, GAO L, XIAO M, et al. Multiscale topology optimization for coated structures with multifarious-microstructural infill[J]. Structural and Multidisciplinary Optimization, 2020, 61(4): 1473-1494. doi: 10.1007/s00158-019-02428-y -
点击查看大图
计量
- 文章访问数: 143
- HTML全文浏览量: 79
- PDF下载量: 28
- 被引次数: 0
