A Fault Diagnosis Method Based on Improved Bat Algorithm Optimization Support Vector Machine
-
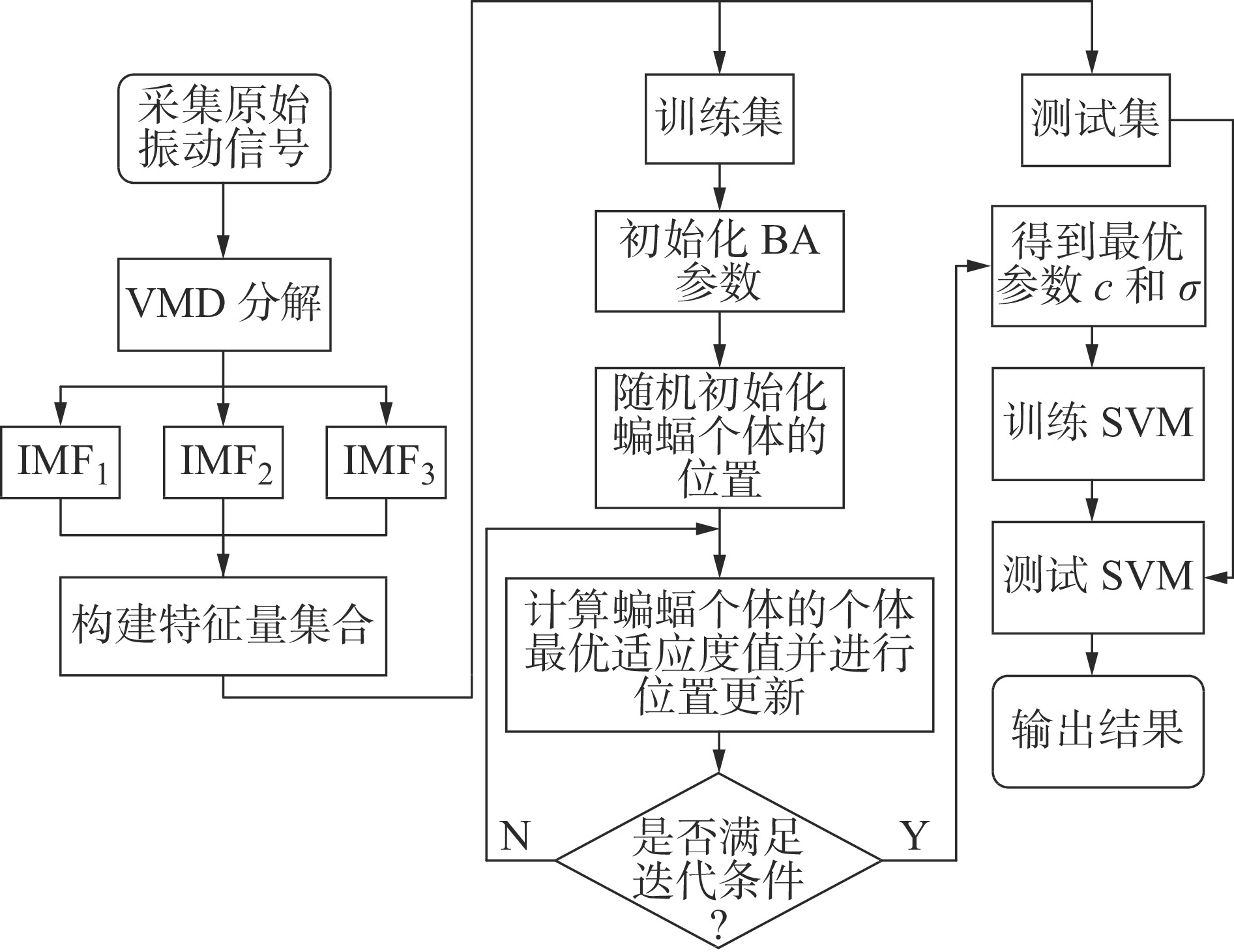
摘要: 提出了一种基于变分模态分解(VMD)和时移多尺度散布熵(TSMDE)的故障特征提取结合改进的蝙蝠算法(IBA)来优化支持向量机(SVM)的滚动轴承故障诊断方法。通过变分模态分解,避免了模式混叠问题,提取各模态分量的散布熵构造故障特征向量,作为故障诊断模型的输入;提出了一种新的自适应速度权重因子用于构建改进的蝙蝠算法以优化支持向量机(IBA-SVM),实现了对不同故障类型的轴承进行分类;利用实验数据对提出的诊断方法进行验证,并与用粒子群算法(PSO)优化支持向量机(PSO-SVM)的诊断方法进行对比。结果表明所提出的方法分类准确率更高,用时更少。Abstract: A rolling bearing fault diagnosis method based on variational mode decomposition (VMD) combined with time-shift multiscale dispersion entropy(TSMDE) fault feature extraction and improved bat algorithm (IBA) in order to optimize support vector machine (SVM)was proposed. Firstly, the problem of mode aliasing was avoidedby means of variational mode decomposition, and the dispersion entropy of each modal component was extracted to construct the fault feature vector, which was used as the input of the fault diagnosis model. Then, a new adaptive speed weight factor was proposed to construct an improved bat algorithm for optimizing support vector machine (IBA-SVM), and the bearings with different fault typeswereclassified. Finally, the experimental data were used to verify the proposed diagnostic method and compared with the particle swarm optimization support vector machine (PSO-SVM) method. The results show that the proposed method has higher classification accuracy and less time.
-
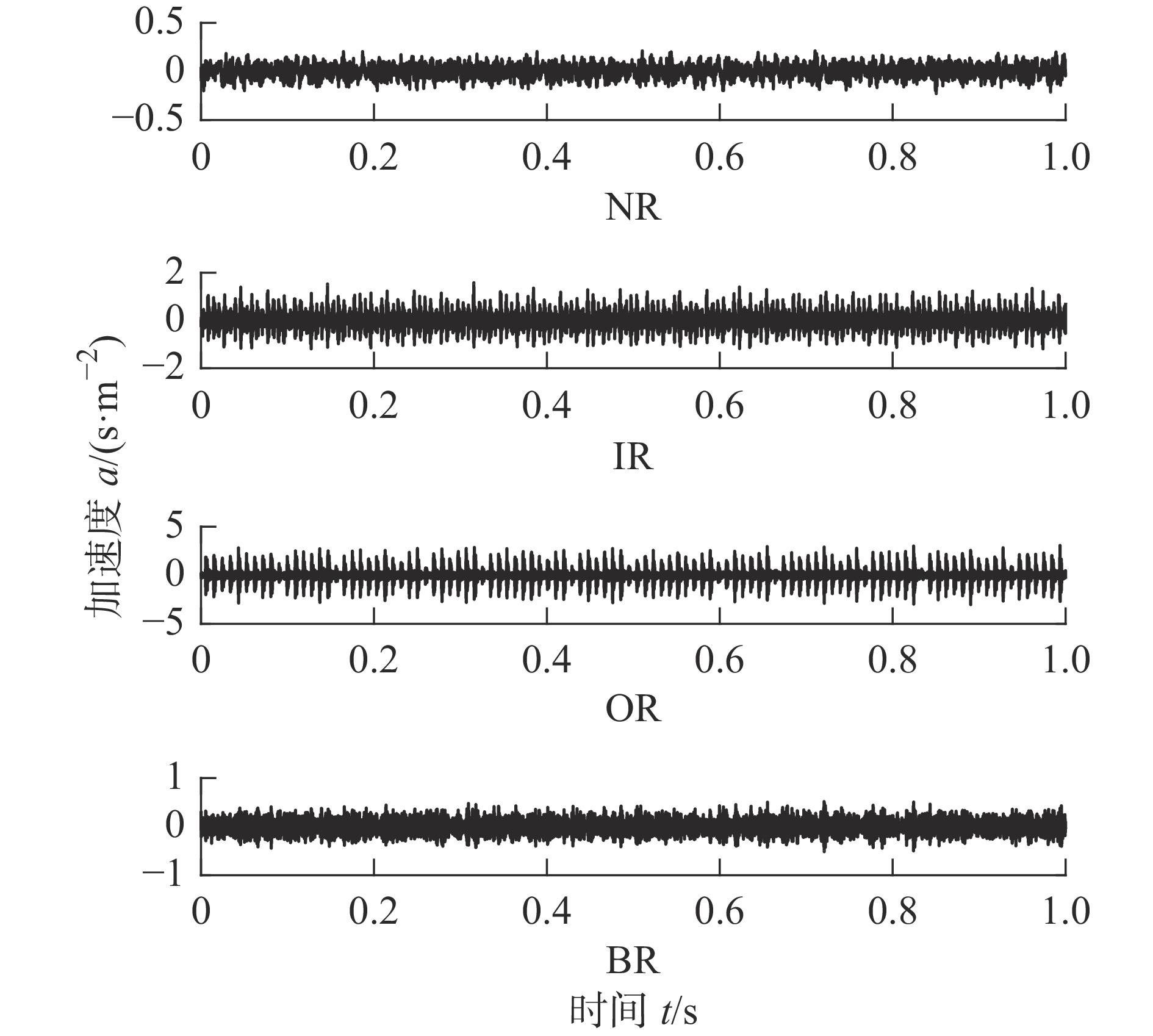
表 1 数据采集装置参数
故障
类型轴承型号 电机转速/
(r·min−1)故障尺寸/
mm采样
频率/
kHz采样
时间/
s内圈
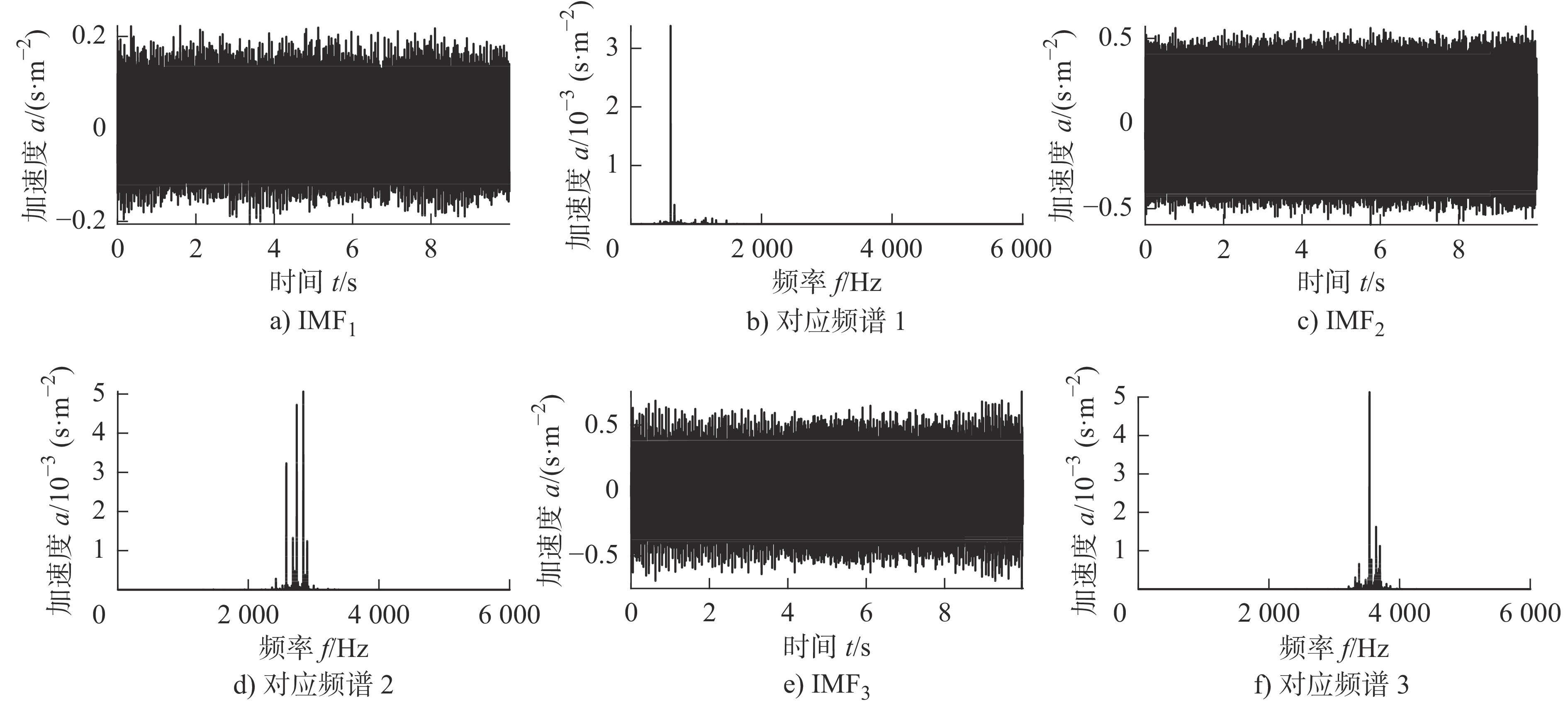
故障6205-2RS JEM SKF 1772 0.177 8 12000 10 表 2 不同分解层数下的中心频率
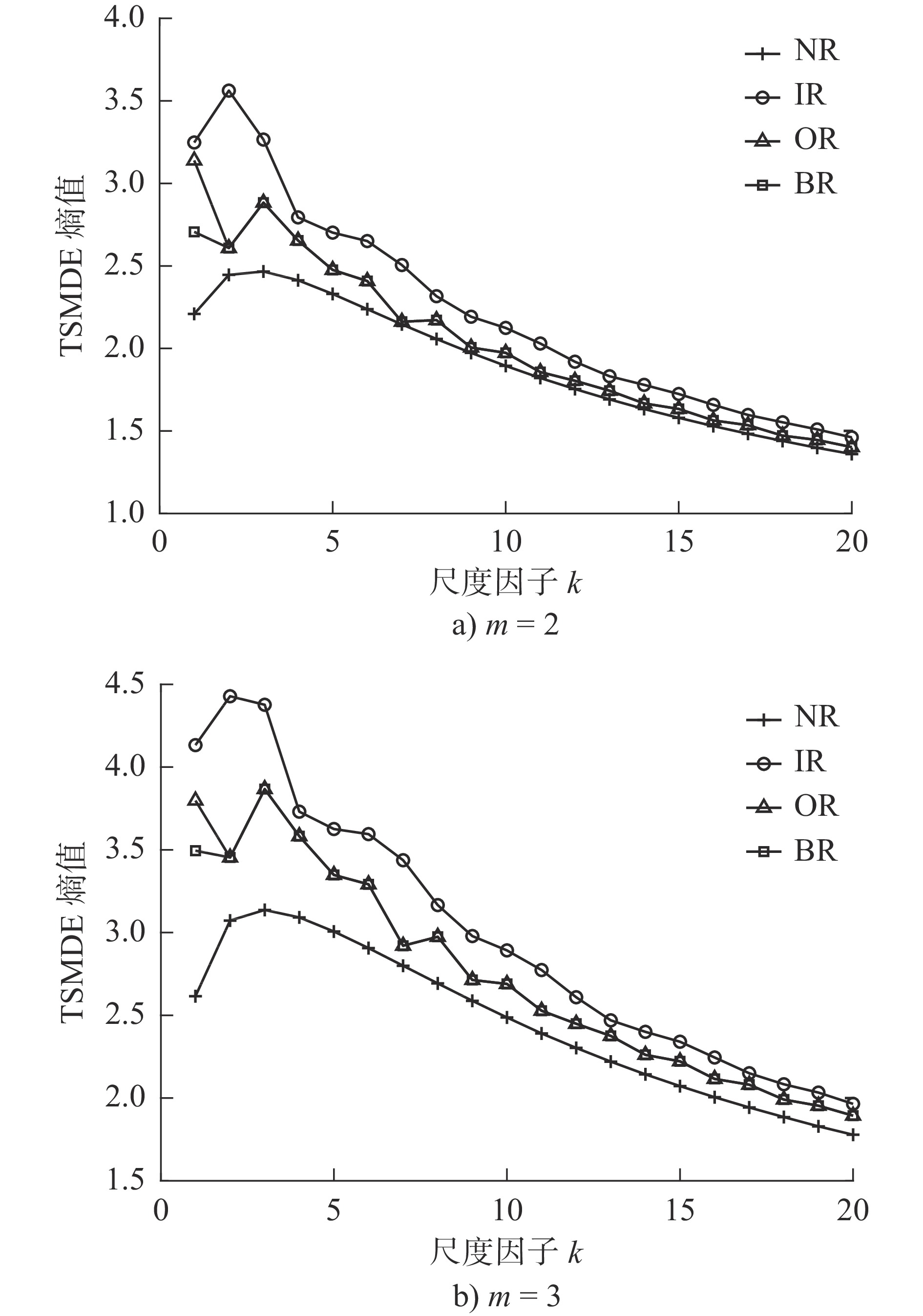
分解层数K 中心频率/Hz 3 691 2757 3572 4 616 1349 2761 3572 5 615 1347 2750 3623 3623 表 3 各模态分量熵值
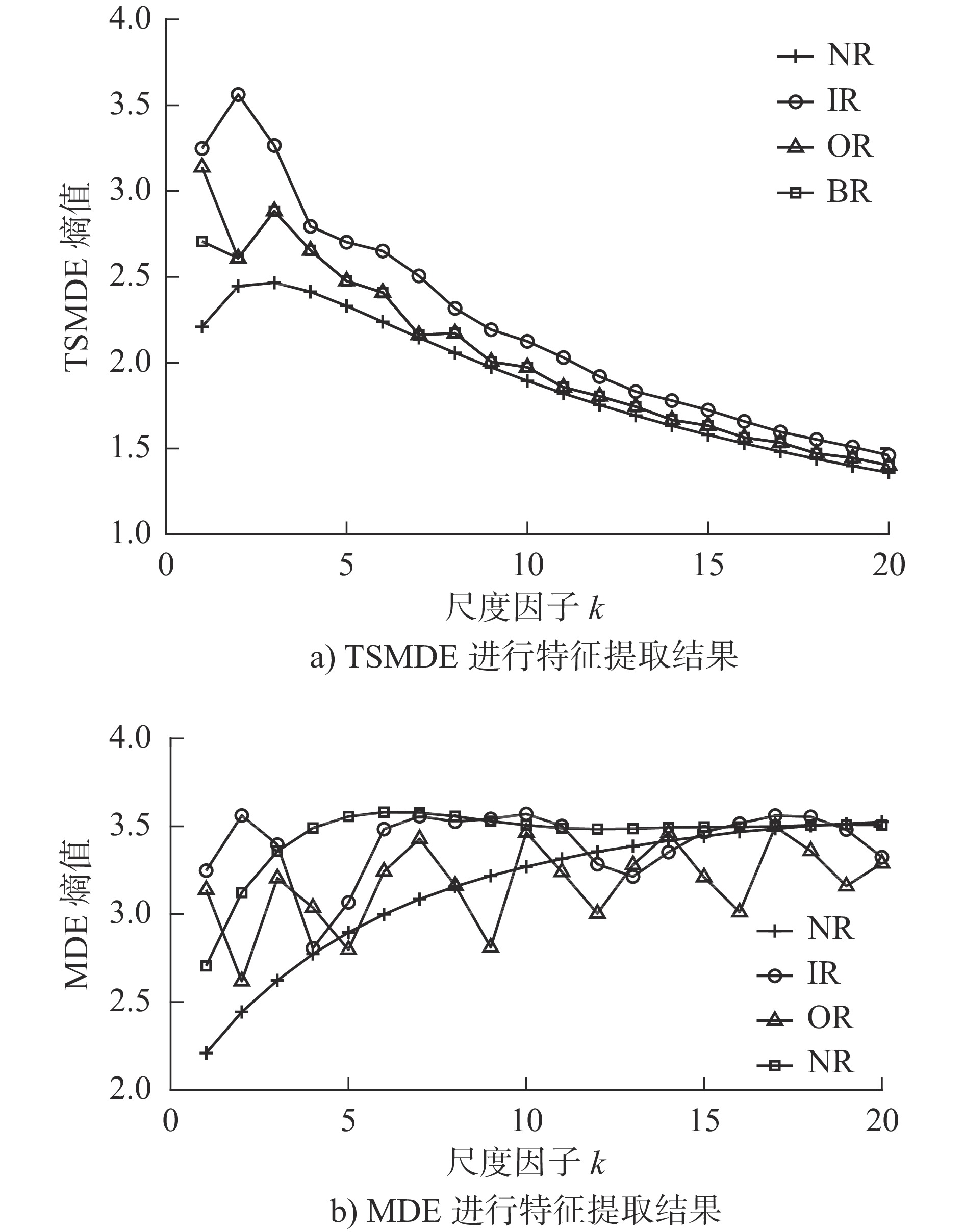
IMF1 IMF2 IMF3 NR 2.2093 3.1791 3.0544 IR 3.2479 3.4435 3.4545 OR 3.5113 3.5294 3.1390 BR 2.7063 3.5787 3.5670 表 4 TSMDE和MDE分类结果
准确率/% 时间/s TSMDE 100 22.62 MDE 93.6 69.84 表 5 IBA算法参数设置
种群
数量变量
维度最大迭代
次数参数c搜索
范围参数σ搜索
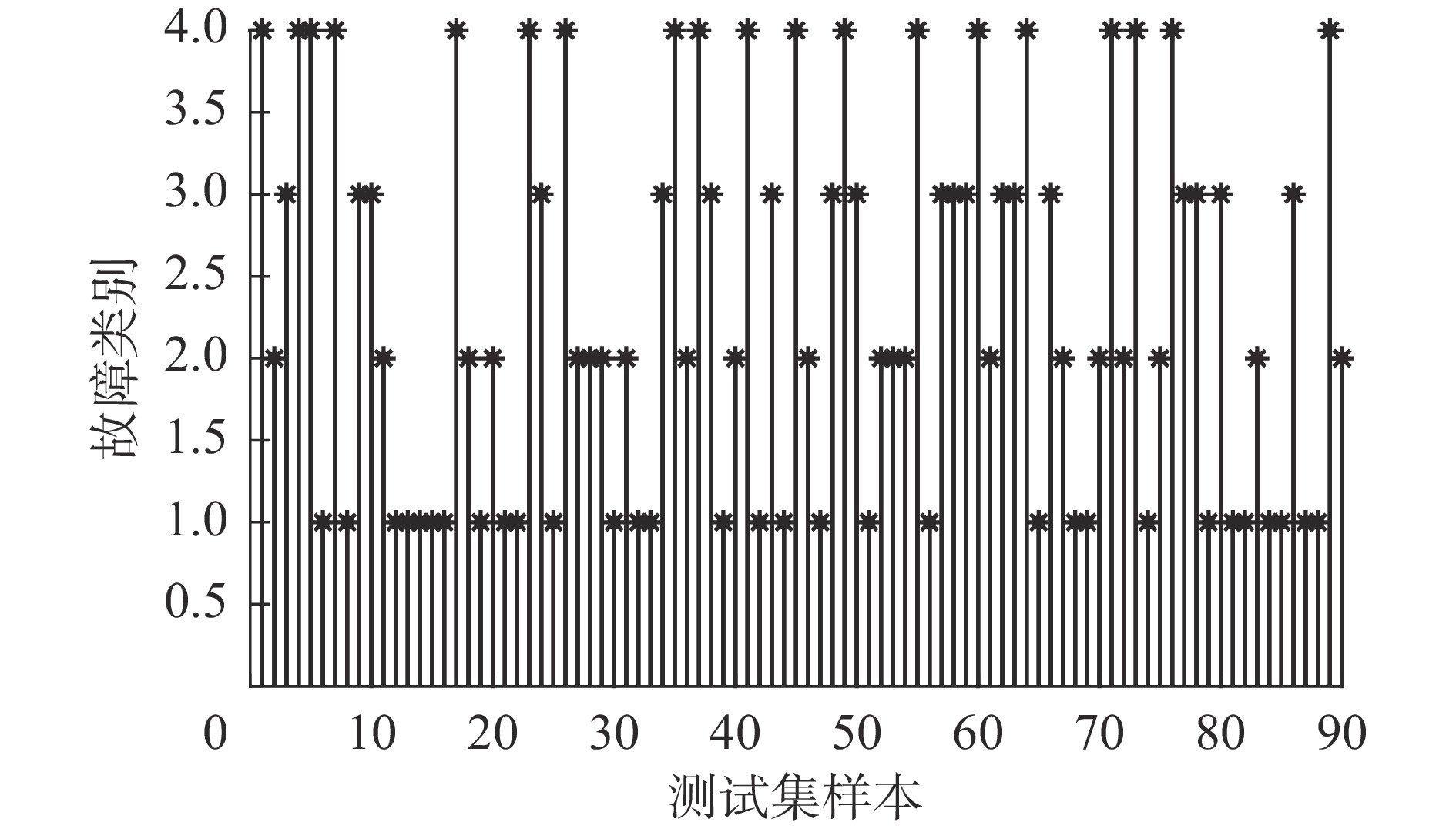
范围50 2 100 [1,100] [1,100] 表 6 3种模型分类结果
模型 准确率/% 时间/s IBA-SVM 100 16.57 BA-SVM 100 20.05 PSO-SVM 100 120.85 -
[1] 李益兵, 王磊, 江丽. 基于PSO改进深度置信网络的滚动轴承故障诊断[J]. 振动与冲击, 2020, 39(5): 89-96. doi: 10.13465/j.cnki.jvs.2020.05.012LI Y B, WANG L, JIANG L. Rolling bearing fault diagnosis based on DBN algorithm improved with PSO[J]. Journal of Vibration and Shock, 2020, 39(5): 89-96. (in Chinese) doi: 10.13465/j.cnki.jvs.2020.05.012 [2] 詹君, 程龙生, 彭宅铭. 基于VMD和改进多分类马田系统的滚动轴承故障智能诊断[J]. 振动与冲击, 2020, 39(2): 32-39. doi: 10.13465/j.cnki.jvs.2020.02.005ZHAN J, CHENG L S, PENG Z M. Intelligent fault diagnosis of rolling bearings based on the VMD and improved multi-classification Mahalanobis Taguchi system[J]. Journal of Vibration and Shock, 2020, 39(2): 32-39. (in Chinese) doi: 10.13465/j.cnki.jvs.2020.02.005 [3] ALI J B, FNAIECH N, SAIDI L, et al. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals[J]. Applied Acoustics, 2015, 89: 16-27. doi: 10.1016/j.apacoust.2014.08.016 [4] WU Z H, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. doi: 10.1142/S1793536909000047 [5] DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. doi: 10.1109/TSP.2013.2288675 [6] LI H, LIU T, WU X, et al. An optimized VMD method and its applications in bearing fault diagnosis[J]. Measurement, 2020, 166: 108185. doi: 10.1016/j.measurement.2020.108185 [7] BANDT C, POMPE B. Permutation entropy: a natural complexity measure for time series[J]. Physical Review Letters, 2002, 88(17): 174102. doi: 10.1103/PhysRevLett.88.174102 [8] RICHMAN J S, MOORMAN J R. Physiological time-series analysis using approximate entropy and sample entropy[J]. American Journal of Physiology-Heart and Circulatory Physiology, 2000, 278(6): H2039-H2049. doi: 10.1152/ajpheart.2000.278.6.H2039 [9] ROSTAGHI M, AZAMI H. Dispersion entropy: a measure for time-series analysis[J]. IEEE Signal Processing Letters, 2016, 23(5): 610-614. doi: 10.1109/LSP.2016.2542881 [10] 王振亚, 姚立纲. 广义精细复合多尺度样本熵与流形学习相结合的滚动轴承故障诊断方法[J]. 中国机械工程, 2020, 31(20): 2463-2471. doi: 10.3969/j.issn.1004-132X.2020.20.009WANG Z Y, YAO L G. Rolling bearing fault diagnosis method based on generalized refined composite multiscale sample entropy and manifold learning[J]. China Mechanical Engineering, 2020, 31(20): 2463-2471. (in Chinese) doi: 10.3969/j.issn.1004-132X.2020.20.009 [11] ZHENG J D, PAN H Y, LIU Q Y, et al. Refined time-shift multiscale normalised dispersion entropy and its application to fault diagnosis of rolling bearing[J]. Physica A:Statistical Mechanics and its Applications, 2020, 545: 123641. doi: 10.1016/j.physa.2019.123641 [12] LI Y X, JIAO S B, GAO X. A novel signal feature extraction technology based on empirical wavelet transform and reverse dispersion entropy[J]. Defence Technology, 2021, 17(5): 1625-1635. doi: 10.1016/j.dt.2020.09.001 [13] SHAO K X, FU W L, TAN J W, et al. Coordinated approach fusing time-shift multiscale dispersion entropy and vibrational Harris hawks optimization-based SVM for fault diagnosis of rolling bearing[J]. Measurement, 2021, 173: 108580. doi: 10.1016/j.measurement.2020.108580 [14] LIU Z W, CAO H R, CHEN X F, et al. Multi-fault classification based on wavelet SVM with PSO algorithm to analyze vibration signals from rolling element bearings[J]. Neurocomputing, 2013, 99: 399-410. doi: 10.1016/j.neucom.2012.07.019 [15] GU Q H, CHANG Y X, LI X H, et al. A novel F-SVM based on FOA for improving SVM performance[J]. Expert Systems With Applications, 2021, 165: 113713. doi: 10.1016/j.eswa.2020.113713 [16] 黎成. 新型元启发式蝙蝠算法[J]. 电脑知识与技术, 2010, 6(23): 6569-6572.LI C. A new metaheuristic bat-inspired algorithm[J]. Computer Knowledge and Technology, 2010, 6(23): 6569-6572. (in Chinese) [17] 朱兴统. 基于蝙蝠算法优化相关向量机的轴承故障诊断方法[J]. 自动化与仪器仪表, 2021(2): 21-24. doi: 10.14016/j.cnki.1001-9227.2021.02.021ZHU X T. Bearing fault diagnosis method based on relevancevector machine optimized by bat algorithm[J]. Automation & Instrumentation, 2021(2): 21-24. (in Chinese) doi: 10.14016/j.cnki.1001-9227.2021.02.021 [18] GOMES G F, CHAVES J A S, DE ALMEIDA F A. An inverse damage location problem applied to AS-350 rotor blades using bat optimization algorithm and multiaxial vibration data[J]. Mechanical Systems and Signal Processing, 2020, 145: 106932. doi: 10.1016/j.ymssp.2020.106932 [19] Bearing Data Center of the Case Western Reserve University[EB/OL].https://csegroups.case.edu -







 下载:
下载: