A Two-way Hausdorff Distance Evaluation Method of Chord Error using NURBS Curve Interpolation
-
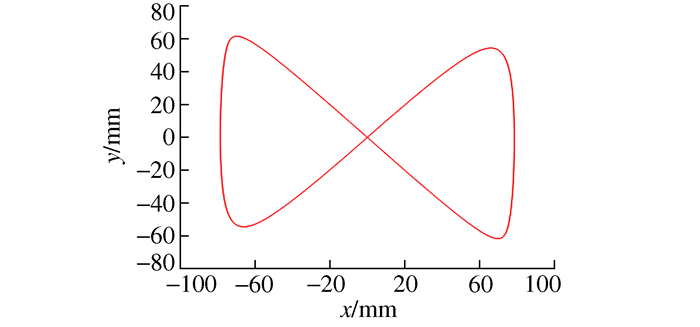
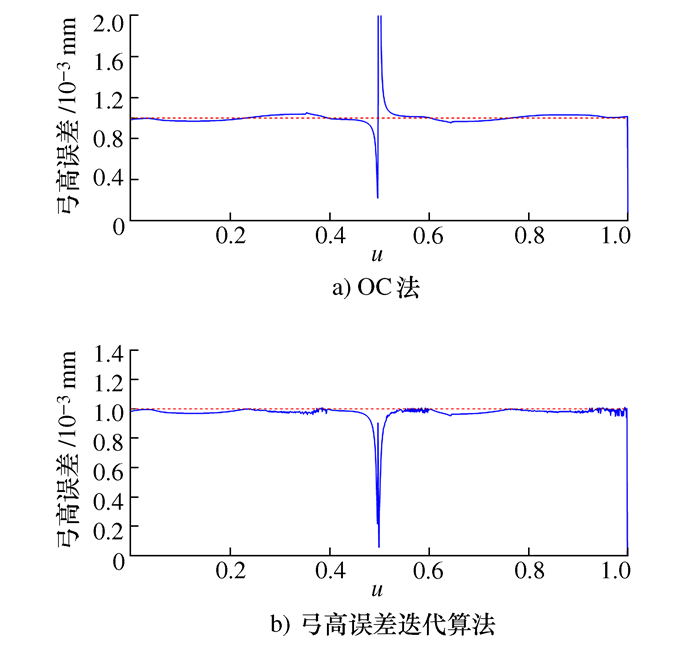
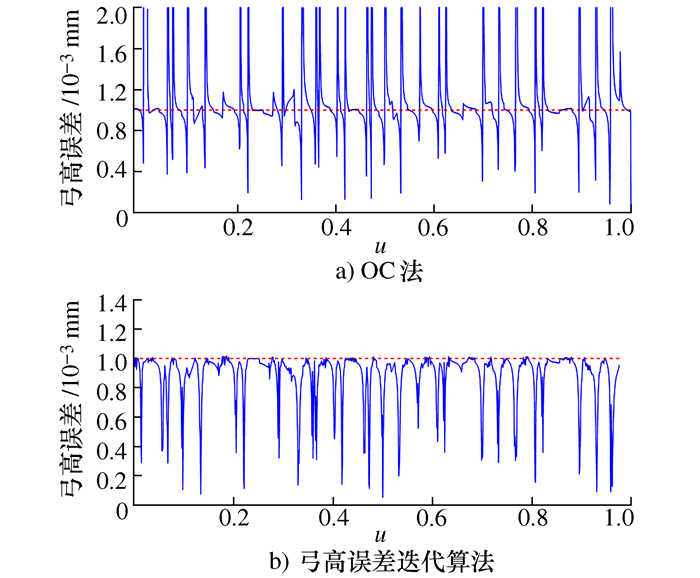
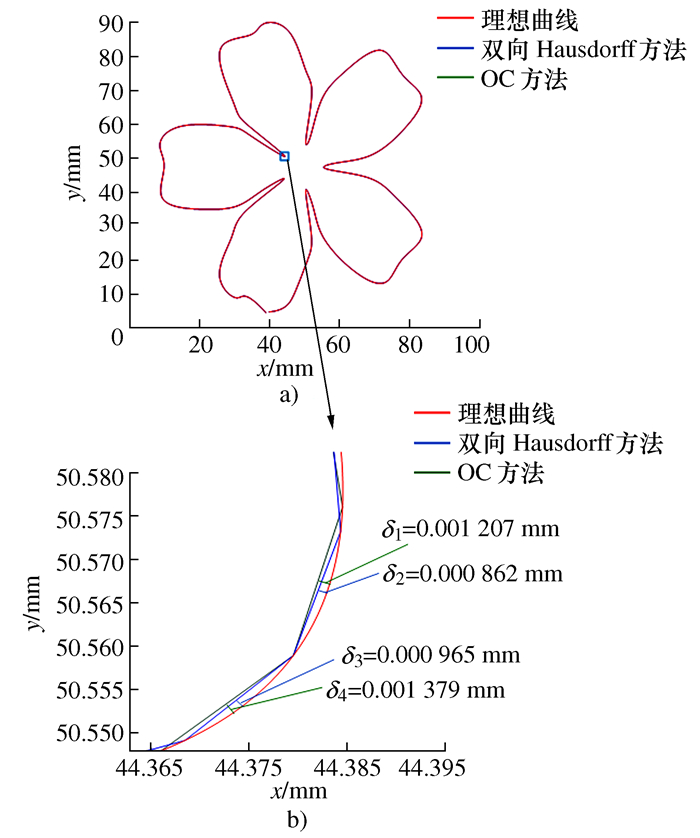
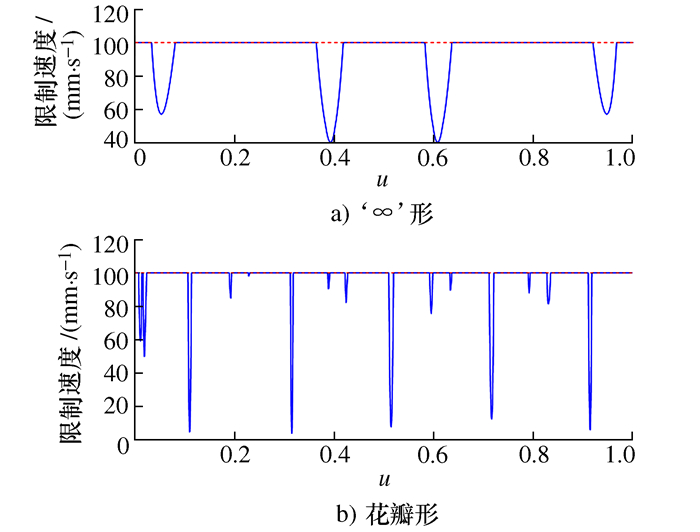
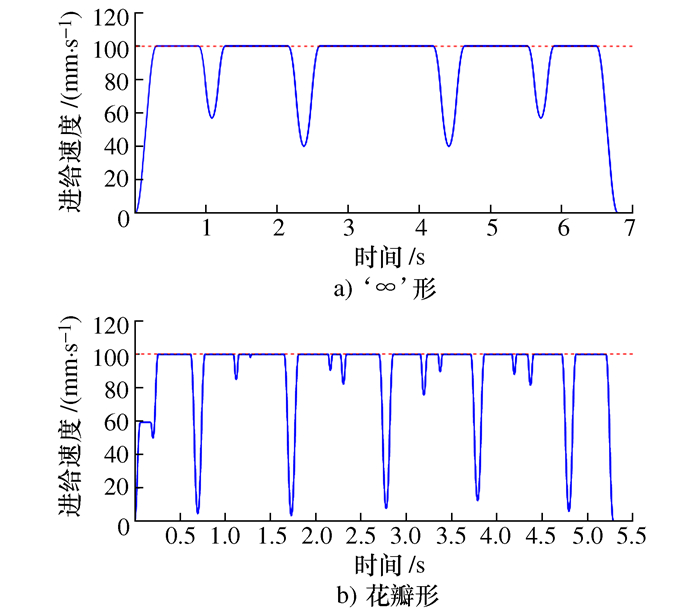
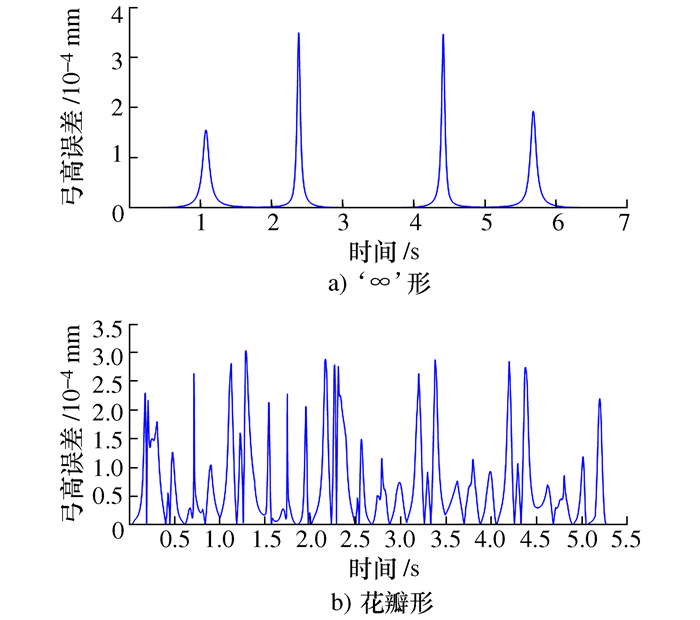
摘要: 数控系统中采用插补方法进行复杂曲线加工会引入弓高误差。利用密切圆(Osculating circle,OC)近似法和单向Hausdorff距离近似法可以获取弓高误差并对其进行后续补偿,但弓高误差求解与补偿精度较低。基于弓高误差的双向Hausdorff距离定义,提出了一种弓高误差的迭代评估算法。该算法能在不考虑曲线复杂度的情况下提升弓高误差的求解精度,并获取满足误差限制要求的最大插补步长,从而进一步生成精确的进给速度限制,防止加工精度及效率因引入其它误差而下降。最后利用该算法对‘∞’形和花瓣形NURBS曲线进行仿真,仿真结果验证了算法的性能及其有效性。
-
关键词:
- 插补法 /
- OC近似法 /
- 弓高误差 /
- 双向Hausdorff距离 /
- NURBS曲线
Abstract: In numerical control system, interpolation is often used to realize complex curve machining, which will introduce some chord errors. The commonly used Osculating Circle(OC) method and single-direction Hausdorff distance method can obtain estimated chord errors, then make subsequent compensations, but they both introduce other errors in the estimation process. For this problem, based on the both-direction Hausdorff distance definition of the chord error, an iterative evaluation algorithm is proposed in this paper. This algorithm can improve the estimation precision of chord error without considering the flexibility of curves, and obtain the maximum interpolation step length that satisfies the error limitation, thereby further generating the accurate feed rate constraints to prevent the reduction of both machining accuracy and efficiency due to the introduction of other errors. Finally, it is simulated by '∞'-shaped and petal-shaped NURBS curves, the simulation results verify the performance and the effectiveness of the proposed algorithm.-
Key words:
- interpolation /
- OC method /
- chord error /
- both-direction Hausdorff distance /
- NURBS curve
-
表 1 仿真系统参数表
参数名称 数值 插补周期Ts 1 ms 最大允许弓高误差δmax 0.001 mm 最大允许进给速度vmax 100 mm/s 最大允许加速度amax 3 000 mm/s2 最大允许加加速度jmax 60 000 mm/s3 最大允许轴向速度vxmax, vymax 100 mm/s 最大允许轴向加速度axmax, aymax 3 000 mm/s2 最大允许轴向加加速度jxmax, jymax 60 000 mm/s3 向心加速度系数M 0.2 表 2 弓高误差评估超限测试点的分析统计表(‘∞’形)
弓高误差评估方法 超限测试点数量 超限测试点占比/% 最大弓高误差/mm OC法 504 50.4 0.194 884 本迭代算法 49 4.9 0.001 013 表 3 弓高误差评估超限测试点的分析统计表(花瓣形)
弓高误差评估方法 超限测试点数量 超限测试点占比/% 最大弓高误差/mm OC法 519 51.9 0.469 542 本迭代算法 67 6.7 0.001 019 -
[1] PIEGL L, TILLER W. The NURBS book[M]. Berlin: Springer, 1997 [2] WANG G X, SHU Q L, WANG J, et al. Research on adaptive non-uniform rational B-spline real-time interpolation technology based on acceleration constraints[J]. The International Journal of Advanced Manufacturing Technology, 2017, 91(5-8): 2089-2100 doi: 10.1007/s00170-016-9914-4 [3] 刘献礼, 周肖阳, 李茂月, 等. NURBS曲线S形加减速寻回实时插补算法[J]. 机械工程学报, 2017, 53(3): 183-192 https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201703024.htmLIU X L, ZHOU X Y, LI M Y, et al. The real-time algorithm of NURBS curve retriever interpolation with S-type acceleration and deceleration control[J]. Journal of mechanical engineering, 2017, 53(3): 183-192 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201703024.htm [4] FAUX I D, PRATT M J. Computational geometry for design and manufacture[M]. New York: Halsted Press, 1979 [5] 赵世田, 赵东标, 付莹莹. 自由曲面加工刀具路径生成高精度变步长算法研究[J]. 机械科学与技术, 2010, 29(1): 32-35 https://www.cnki.com.cn/Article/CJFDTOTAL-JXKX201001009.htmZHAO S T, ZHAO D B, FU Y Y. High precision algorithm of variable forward step planning for tool path generation of freeform surface[J]. Mechanical Science and Technology for Aerospace Engineering, 2010, 29(1): 32-35 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXKX201001009.htm [6] DU X, HUANG J, ZHU L M, et al. Third-order chord error estimation for freeform contour in computer-aided manufacturing and computer numerical control systems[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2019, 233(3): 863-874 doi: 10.1177/0954405418757266 [7] 王太勇, 尤中桐, 辛全琦. 螺旋线插补速度规划及其插补参数求解方法[J]. 天津大学学报(自然科学与工程技术版), 2018, 51(11): 1107-1116 https://www.cnki.com.cn/Article/CJFDTOTAL-TJDX201811001.htmWANG T Y, YOU Z T, XIN Q Q. Spiral interpolation velocity planning and method of solving interpolation parameters[J]. Journal of Tianjin University (Science and Technology), 2018, 51(11): 1107-1116 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDX201811001.htm [8] LEE R S, SHE C H. Tool path generation and error control method for multi-axis NC machining of spatial cam[J]. International Journal of Machine Tools and Manufacture, 1998, 38(4): 277-290 doi: 10.1016/S0890-6955(97)00043-6 [9] YEH S S, HSU P L. Adaptive-feedrate interpolation for parametric curves with a confined chord error[J]. Computer-Aided Design, 2002, 34(3): 229-237 doi: 10.1016/S0010-4485(01)00082-3 [10] YONG T, NARAYANASWAMI R. A parametric interpolator with confined chord errors, acceleration and deceleration for NC machining[J]. Computer-Aided Design, 2003, 35(13): 1249-1259 doi: 10.1016/S0010-4485(03)00043-5 [11] LI J G, LIU Y, LI Y N, et al. S-model speed planning of NURBS curve based on uniaxial performance limitation[J]. IEEE Access, 2019, 7: 60837-60849 doi: 10.1109/ACCESS.2019.2914509 [12] FAN W, GAO X S, YAN W, et al. Interpolation of parametric CNC machining path under confined jounce[J]. The International Journal of Advanced Manufacturing Technology, 2012, 62(5-8): 719-739 doi: 10.1007/s00170-011-3842-0 [13] HUANG J, ZHU L M. Feedrate scheduling for interpolation of parametric tool path using the sine series representation of jerk profile[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2017, 231(13): 2359-2371 doi: 10.1177/0954405416629588 [14] 陈爽, 张悦, 张勤俭, 等. 一种基于B样条插值的机器人速度规划算法[J]. 应用基础与工程科学学报, 2018, 26(3): 661-671 https://www.cnki.com.cn/Article/CJFDTOTAL-YJGX201803019.htmCHEN S, ZHANG Y, ZHANG Q J, et al. A kind of robot speed planning algorithm based on B-spline interpolation[J]. Journal of Basic Science and Engineering, 2018, 26(3): 661-671 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YJGX201803019.htm [15] 聂明星, 蒋新华, 陈兴武. 基于速度敏感区尖点的NURBS曲线分段插补方法[J]. 信息与控制, 2013, 42(6): 714-722 https://www.cnki.com.cn/Article/CJFDTOTAL-XXYK201306009.htmNIE M X, JIANG X H, CHEN X W. NURBS curve piecewise interpolation method based on the tips of velocity sensitive areas[J]. Information and Control, 2013, 42(6): 714-722 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XXYK201306009.htm [16] 吴玉香, 王鹏. 基于Runge-Kutta的NURBS曲线实时前瞻插补算法[J]. 华南理工大学学报(自然科学版), 2017, 45(10): 121-128 doi: 10.3969/j.issn.1000-565X.2017.10.017WU Y X, WANG P. A real-time look-ahead interpolation algorithm for NURBS curves based on Runge-Kutta[J]. Journal of South China University of Technology (Natural Science Edition), 2017, 45(10): 121-128 (in Chinese) doi: 10.3969/j.issn.1000-565X.2017.10.017 [17] 高翔宇, 刘晓健, 裘乐淼, 等. 基于曲率约束和位移补偿的NURBS曲线柔性高精插补方法[J]. 计算机辅助设计与图形学学报, 2018, 30(12): 2213-2223 https://www.cnki.com.cn/Article/CJFDTOTAL-JSJF201812003.htmGAO X Y, LIU X J, QIU L M, et al. NURBS curve interpolation method with flexibility and high accuracy based on curvature constraint and displacement compensation[J]. Journal of Computer-Aided Design & Computer Graphics, 2018, 30(12): 2213-2223 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSJF201812003.htm [18] 邬再新, 李华兵. 神经网络在自由曲线插补中的应用研究[J]. 组合机床与自动化加工技术, 2019(2): 49-52 https://www.cnki.com.cn/Article/CJFDTOTAL-ZHJC201902013.htmWU Z X, LI H B. Research on the application of neural network in free curve interpolation[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2019(2): 49-52 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZHJC201902013.htm [19] 董海涛, 潘海鸿, 黄丽宇, 等. 一种优化的NURBS曲线插补算法[J]. 计算机集成制造系统, 2014, 20(9): 2172-2177 https://www.cnki.com.cn/Article/CJFDTOTAL-JSJJ201409011.htmDONG H T, PAN H H, HUANG L Y, et al. Optimized NURBS curve interpolation algorithm[J]. Computer Integrated Manufacturing Systems, 2014, 20(9): 2172-2177 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSJJ201409011.htm [20] 罗钧, 汪俊, 刘学明, 等. 基于S型加减速的自适应前瞻NURBS曲线插补算法[J]. 计算机集成制造系统, 2013, 19(1): 55-60 https://www.cnki.com.cn/Article/CJFDTOTAL-JSJJ201301008.htmLUO J, WANG J, LIU X M, et al. Adaptive NURBS interpolation algorithm with look-ahead function based on S-shape acceleration/deceleration[J]. Computer Integrated Manufacturing Systems, 2013, 19(1): 55-60 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSJJ201301008.htm [21] 施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 北京: 高等教育出版社, 2001SHI F Z. Computer aided geometric design and non-uniform rational B-spline[M]. Beijing: Higher Education Press, 2001 (in Chinese) [22] 江本赤, 王建彬, 苏学满. 一种双NURBS曲线的参数迭代插补算法[J]. 机械科学与技术, 2019, 38(5): 754-760 doi: 10.13433/j.cnki.1003-8728.20180225JIANG B C, WANG J B, SU X M. An interpolation algorithm by parametric-iteration for dual-NURBS curve[J]. Mechanical Science and Technology for Aerospace Engineering, 2019, 38(5): 754-760 (in Chinese) doi: 10.13433/j.cnki.1003-8728.20180225 [23] 蔡安江, 杜金健, 宋仁杰, 等. 五轴加工刀具轨迹NURBS插补技术的研究[J]. 机械科学与技术, 2017, 36(3): 402-408 doi: 10.13433/j.cnki.1003-8728.2017.0313CAI A J, DU J J, SONG R J, et al. Study on NURBS interpolation technology of five-axis machining tool path[J]. Mechanical Science and Technology for Aerospace Engineering, 2017, 36(3): 402-408 (in Chinese) doi: 10.13433/j.cnki.1003-8728.2017.0313 [24] LAI J Y, LIN K Y, TSENG S J, et al. On the development of a parametric interpolator with confined chord error, feedrate, acceleration and jerk[J]. The International Journal of Advanced Manufacturing Technology, 2008, 37(1-2): 104-121[24] doi: 10.1007/s00170-007-0954-7 [25] LI J G, LIU Y, LI Y N, et al. S-model speed planning of NURBS curve based on uniaxial performance limitation[J]. IEEE Access, 2019, 7: 60837-60849 doi: 10.1109/ACCESS.2019.2914509 [26] ZHONG W B, LUO X C, CHANG W L, et al. A real-time interpolator for parametric curves[J]. International Journal of Machine Tools and Manufacture, 2018, 125: 133-145 doi: 10.1016/j.ijmachtools.2017.11.010 -







 下载:
下载: