Analysis of Flexibility of 3-PSS Flexible Parallel Micromanipulation Robot
-
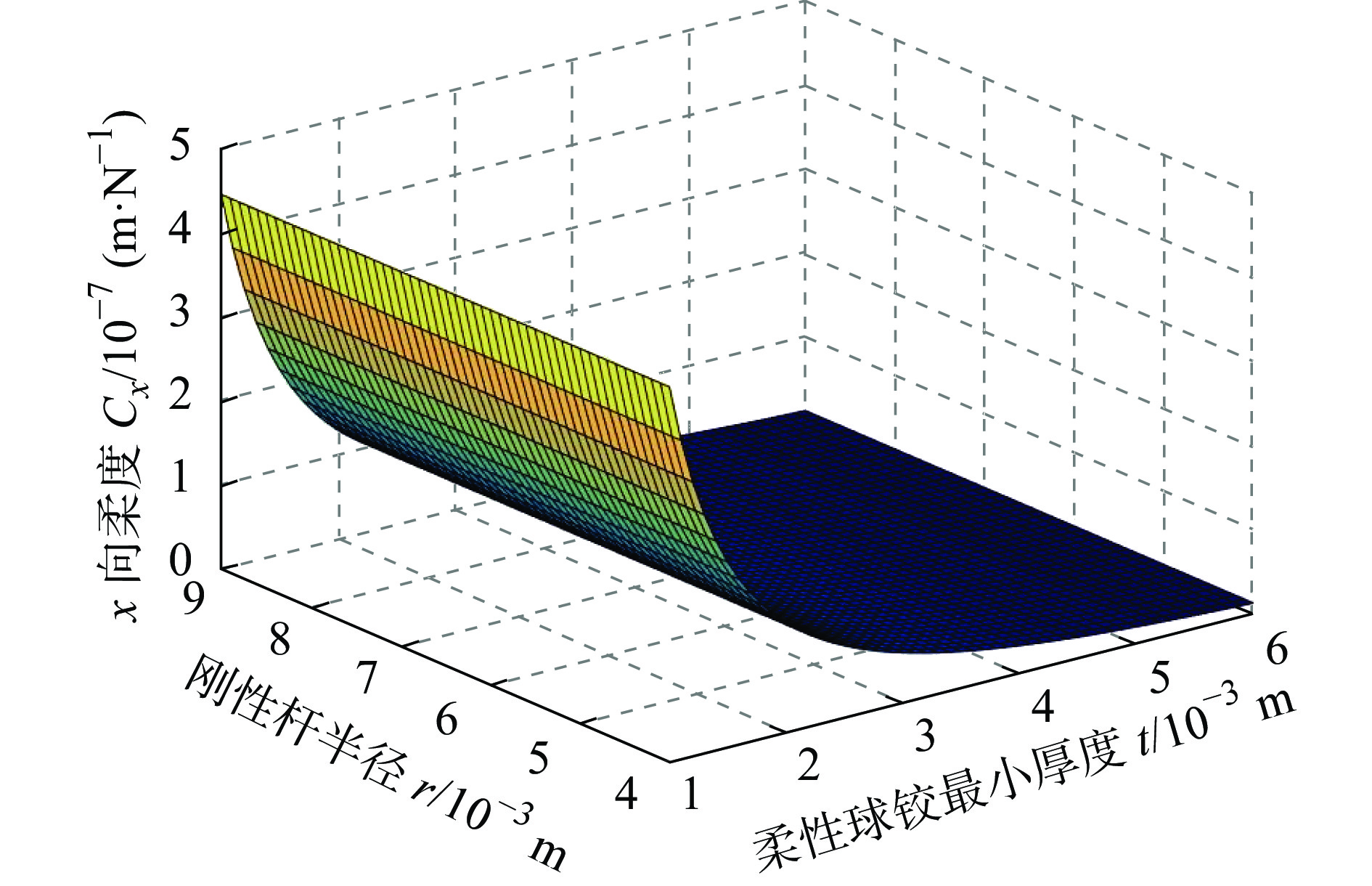
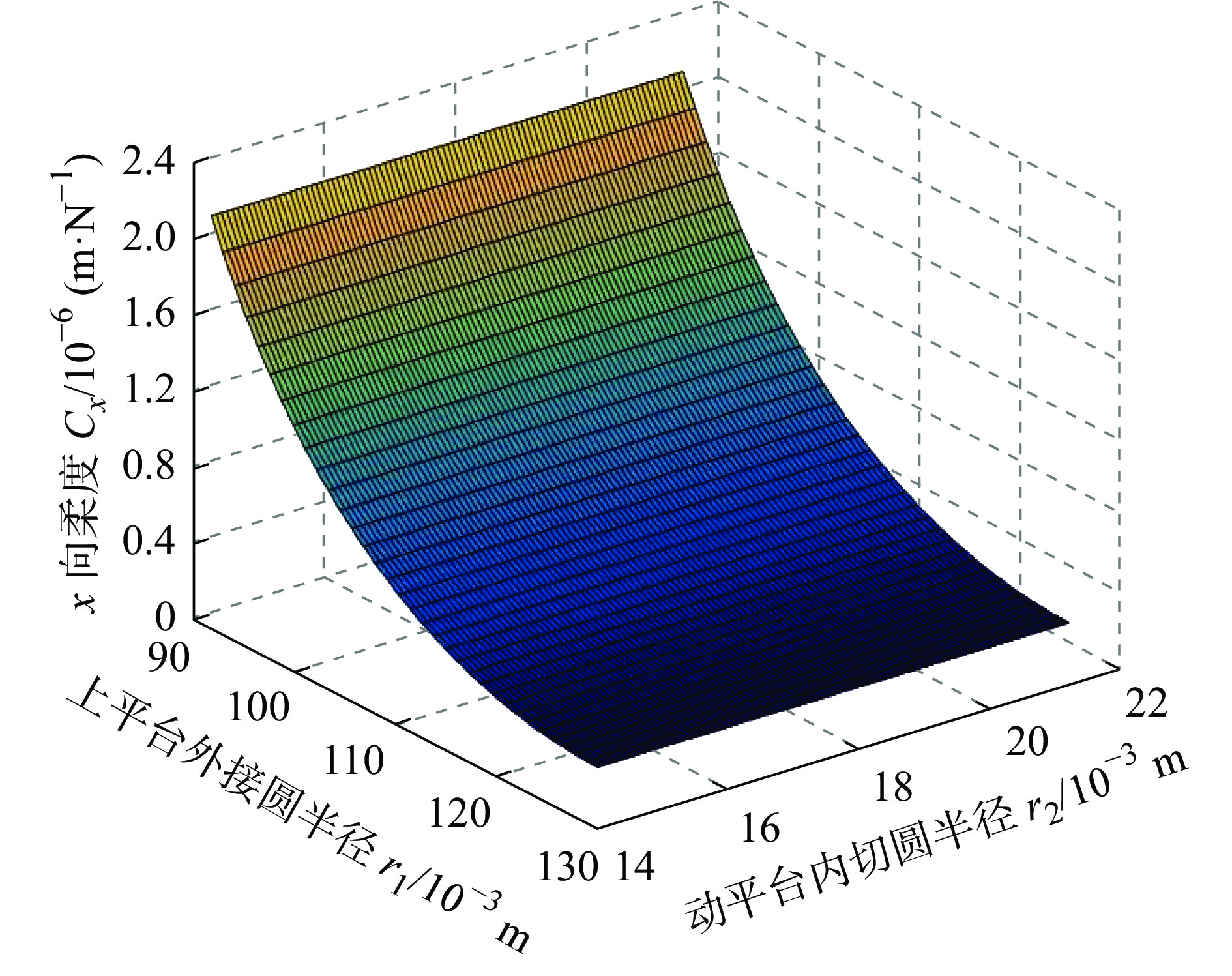
摘要: 柔度矩阵建模是进行全柔性机构分析的基础。针对3-PSS型柔性并联微操作机器人,首先基于坐标变换法计算机构单条支链柔度矩阵,并基于此建立机器人整体柔度矩阵模型。然后进行数值算例计算和Ansys有限元仿真分析,并将理论计算结果与有限元分析结果进行对比,验证了柔度矩阵建模的正确性。最后对柔性并联机器人进行了柔度性能分析,并得出了机构的结构参数对柔度的影响规律,分析结果对3-PSS型柔性并联机构的结构优化设计提供了依据。Abstract: Compliance matrix modeling is the basis for analyzing the fully flexible mechanisms. For the 3-PSS type flexible parallel micro-manipulation robot, the compliance matrix of a single branch of the mechanism is calculated based on the coordinate transformation method, and the overall compliance matrix model for robot is established. Then, numerical calculation examples and ANSYS finite element simulation analysis are performed, and the calculated results are compared with the finite element analysis results to verify the correctness of the compliance matrix modeling. Finally, the flexibility performance of the flexible parallel robots is analyzed, and the influence of the structure parameters of the mechanism on the flexibility is obtained. The analysis results provide a basis for the structural optimization design of the 3-PSS flexible parallel mechanism.
-
Key words:
- 3-PSS mechanism /
- flexible parallel robot /
- coordinate transformation /
- compliance matrix
-
表 1 3-PSS柔性并联微操作机器人结构参数
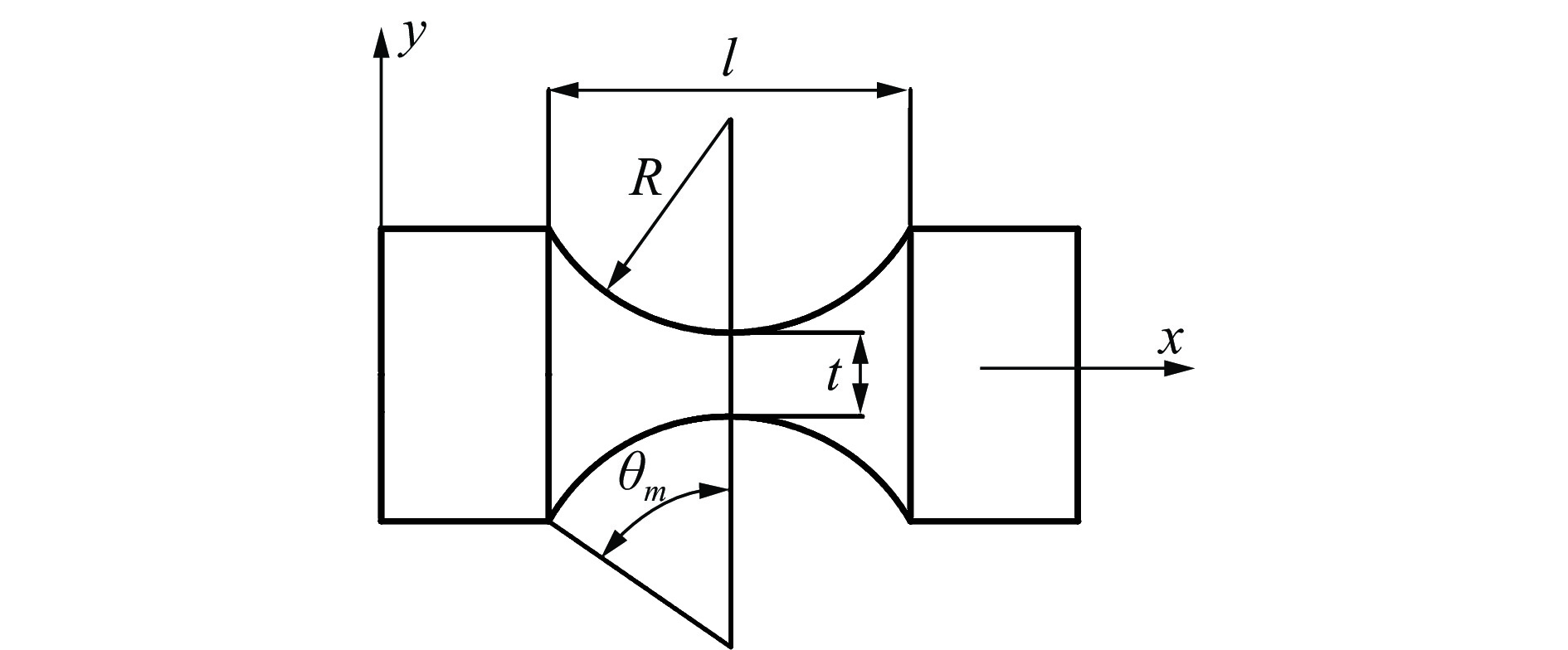
参数 数值 参数 数值 柔性球铰材料 65Mn 柔性球铰切割半径R/mm 2.5 杨氏模量E/GPa 200 圆弧的圆心角θm/(°) 60 泊松比ν 0.3 刚性杆长度L/mm 120 t/mm 1 上平台外接圆半径r1/mm 103 刚性杆半径r/mm 5 动平台内切圆半径r2 /mm 18 表 2 3-PSS柔性并联微操作机器人柔度分析结果
柔度/(m·N−1) 理论模型 有限元模型 误差/% x向Cx 4.316×10−7 4.572×10−7 5.6 y向Cy 4.316×10−7 4.572×10−7 5.6 z向Cz 2.260 3×10−8 2.419×10 −8 6.5 -
[1] 徐洪业. 空间3-DOF柔性并联微操作平台的设计与分析[D]. 天津: 天津理工大学, 2018.XU H Y. Design and analysis of spatial 3-DOF flexible parallel micromanipulation stage[D]. Tianjin: School of Mechanical Engineering, Tianjin University of Technology, 2018. (in Chinese) [2] 左行勇, 刘晓明. 三种形状柔性铰链转动刚度的计算与分析[J]. 仪器仪表学报, 2006, 27(12): 1725-1728. doi: 10.3321/j.issn:0254-3087.2006.12.038ZUO X Y, LIU X M. Calculation and analysis of rotational stiffness for three types of flexure hinges[J]. Chinese Journal of Scientific Instrument, 2006, 27(12): 1725-1728. (in Chinese) doi: 10.3321/j.issn:0254-3087.2006.12.038 [3] 杨启志, 尹小琴, 马履中, 等. 数值法建立单向柔性铰链的刚度矩阵[J]. 农业机械学报, 2005, 36(1): 104-107. doi: 10.3969/j.issn.1000-1298.2005.01.028YANG Q Z, YIN X Q, MA L Z, et al. Numerical analysis for establishing stiffness matrix of the compliant joint[J]. Transactions of the Chinese Society for Agricultural Machinery, 2005, 36(1): 104-107. (in Chinese) doi: 10.3969/j.issn.1000-1298.2005.01.028 [4] 陈应舒, 朱淳逸. 椭圆弧型柔性球铰的柔度矩阵计算与分析[J]. 机械设计与研究, 2015, 31(5): 51-54 + 61. doi: 10.13952/j.cnki.jofmdr.2015.0183CHEN Y S, ZHU C Y. Calculation and analysis of flexibility matrix of elliptic arc flexure spherical hinge[J]. Machine Design & Research, 2015, 31(5): 51-54 + 61. (in Chinese) doi: 10.13952/j.cnki.jofmdr.2015.0183 [5] 杨春辉, 刘平安. 圆弧型柔性球铰柔度设计计算[J]. 工程设计学报, 2014, 21(4): 389-392 + 404. doi: 10.3785/j.issn.1006-754X.2014.04.014YANG C H, LIU P A. Design and calculation of compliance of arc flexure spherical hinge[J]. Chinese Journal of Engineering Design, 2014, 21(4): 389-392 + 404. (in Chinese) doi: 10.3785/j.issn.1006-754X.2014.04.014 [6] 吴鹰飞, 周兆英. 柔性铰链的计算和分析[J]. 机械设计与研究, 2002, 18(3): 29-30. doi: 10.3969/j.issn.1006-2343.2002.03.009WU Y F, ZHOU Z Y. Design calculation and analysis of flexure hinge[J]. Machine Design & Research, 2002, 18(3): 29-30. (in Chinese) doi: 10.3969/j.issn.1006-2343.2002.03.009 [7] 于靖军, 毕树生, 宗光华. 空间全柔性机构位置分析的刚度矩阵法[J]. 北京航空航天大学学报, 2002, 28(3): 323-326. doi: 10.3969/j.issn.1001-5965.2002.03.021YU J J, BI S S, ZONG G H. Stiffness matrix method for displacement analysis of fully spatial compliant mechanisms[J]. Journal of Beijing University of Aeronautics and Astronautics, 2002, 28(3): 323-326. (in Chinese) doi: 10.3969/j.issn.1001-5965.2002.03.021 [8] 杨启志, 马履中, 谢俊, 等. 三平移全柔性并联微动机器人机构静力学分析[J]. 农业机械学报, 2007, 38(11): 110-113. doi: 10.3969/j.issn.1000-1298.2007.11.027YANG Q Z, MA L Z, XIE J, et al. Static forces analysis of the fully compliant three DOF translational parallel mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(11): 110-113. (in Chinese) doi: 10.3969/j.issn.1000-1298.2007.11.027 [9] 闵健. 基于刚度矩阵法的柔性机构设计平台开发[D]. 大连: 大连理工大学, 2015MIN J. Development of compliant mechanism design platform based on the stiffness matrix method[D]. Dalian: Dalian University of Technology, 2015. (in Chinese) [10] 纪竹青. 柔性手术机器人的刚度调控技术研究[D]. 沈阳: 沈阳理工大学, 2018JI Z Q. The research on stiffness controlling technology of the flexible surgical robot[D]. Shenyang: Shenyang Ligong University, 2018. (in Chinese) [11] 张明, 房立金, 孙凤, 等. 变刚度柔性机器人关节的设计与解耦控制方法[J]. 电机与控制学报, 2019, 23(7): 120-128. doi: 10.15938/j.emc.2019.07.015ZHANG M, FANG L J, SUN F, et al. Design and decoupling control of variable-stiffness flexible robot joint[J]. Electric Machines and Control, 2019, 23(7): 120-128. (in Chinese) doi: 10.15938/j.emc.2019.07.015 [12] 李建钢, 杨桂林, 张林, 等. 基于柔性并联机构的变刚度夹持器设计分析[J]. 机械工程学报, 2019, 55(21): 64-72.LI J G, YANG G L, ZHANG L, et al. Design analysis of a variable stiffness gripper based on flexible parallel mechanism[J]. Journal of Mechanical Engineering, 2019, 55(21): 64-72. (in Chinese) [13] 邵忠喜, 吴石磊, 富宏亚. 一种新型大口径光栅拼接柔性定位机构刚度分析[J]. 机械工程学报, 2018, 54(13): 117-125. doi: 10.3901/JME.2018.13.117SHAO Z X, WU S L, FU H Y. Stiffness analysis of a novel flexible positioning mechanism for large-aperture grating tiling[J]. Journal of Mechanical Engineering, 2018, 54(13): 117-125. (in Chinese) doi: 10.3901/JME.2018.13.117 [14] 于靖军, 毕树生, 宗光华, 等. 3自由度柔性微机器人的静刚度分析[J]. 机械工程学报, 2002, 38(4): 7-10. doi: 10.3321/j.issn:0577-6686.2002.04.002YU J J, BI S S, ZONG G H, et al. Analysis for the static stiffness of a 3DOF parallel compliant micromanipulator[J]. Journal of Mechanical Engineering, 2002, 38(4): 7-10. (in Chinese) doi: 10.3321/j.issn:0577-6686.2002.04.002 [15] 杨春辉, 刘平安. 基于坐标转换法的3-RRR并联微动机构柔度矩阵建模[J]. 机械传动, 2017, 41(6): 80-84. doi: 10.16578/j.issn.1004.2539.2017.06.015YANG C H, LIU P A. Modeling of the flexibility matrix of 3-RRR parallel micromanipulator based on coordinate transformation method[J]. Journal of Mechanical Transmission, 2017, 41(6): 80-84. (in Chinese) doi: 10.16578/j.issn.1004.2539.2017.06.015 [16] NI Y, DENG Z Q, WU X, et al. Modeling and analysis of an over-constrained flexure-based compliant mechanism[J]. Measurement, 2014, 50: 270-278. doi: 10.1016/j.measurement.2014.01.020 [17] 任军, 何文浩. 3-PSS柔性并联微操作机器人运动学及工作空间分析[J]. 机械设计与制造, 2022, 382(12): 58-63.REN J, HE W H. Kinematics and workspace analysis of 3-PSS flexible parallel micromanipulator[J]. Machinery Design & Manufacture, 2022, 382(12): 58-63. (in Chinese) [18] 于靖军, 毕树生, 裴旭, 等. 柔性设计: 柔性机构的分析与综合[M]. 北京: 高等教育出版社, 2018: 107-114YU J J, BI S S, PEI X, et al. Flexure design: analysis and synthesis of compliant mechanism[M]. Beijing: Higher Education Press, 2018: 107-114. (in Chinese) -







 下载:
下载: