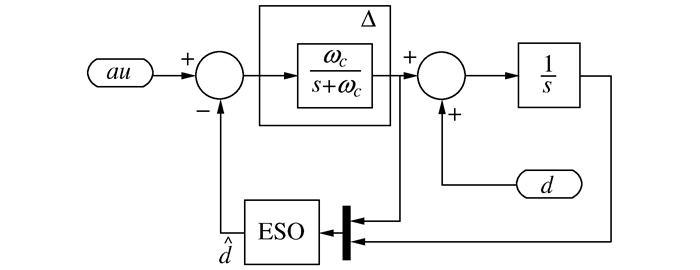
Proximate Time Optimal EMA Position Servo Control Strategy
-
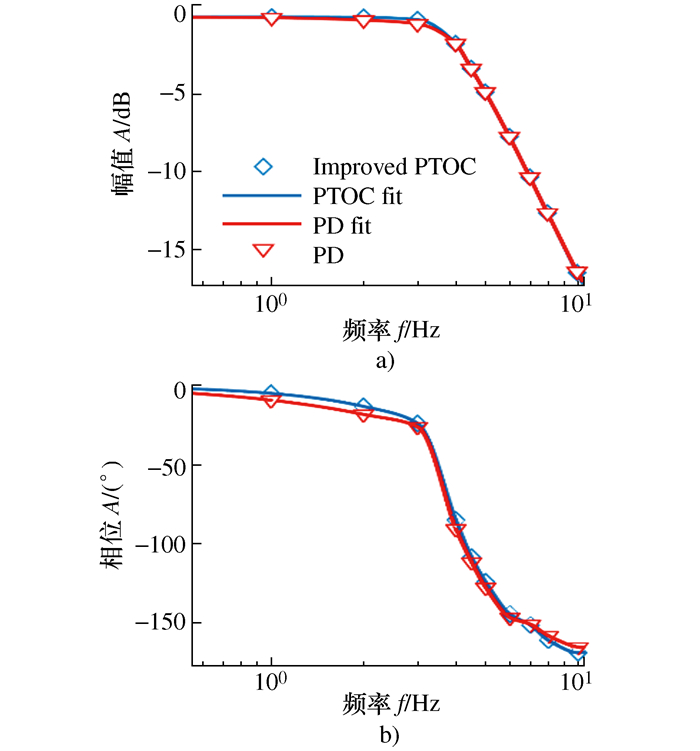
摘要: 针对EMA(机电作动器)伺服系统中常见的速度限幅处理以及高动态响应要求, 提出了一种基于1阶LADRC(线性自抗扰控制算法)速度环的PTOC(鲁棒近似时间最优位置控制)控制策略。将速度环与位置环控制律进行结合, 避免一般PTOC伺服系统中对速度控制律与位置控制律的切换。分析了速度环不同工作状态下对PTOC控制律的影响, 分别设计了速度环饱和以及非饱和工作状态下的PTOC控制律。针对典型PTOC控制律中参数选择过于保守的问题, 提出了一种基于可变切换区和线性区的改进方法, 并且给出了稳定性证明。仿真实验结果表明, 提出的控制策略能够有效提高EMA的位置伺服动态性能以及对扰动的抵抗能力。Abstract: To satisfy speed limit requirements and high dynamic response requirements for an EMA (electro-mechanical actuator) servo system, a robust PTOC (approximate time optimal control) position control strategy based on the first-order linear active disturbance rejection control speed controller is proposed. By combining speed loop dynamics with position loop control laws, the switching between speed control law and position control law in the general PTOC servo system is avoided. The effect of the speed controller on the PTOC control law under different working conditions is analyzed, and the PTOC control law under the saturated and unsaturated working conditions of the speed loop is proposed respectively. To solve the problem of conservative parameter selection with the typical PTOC control law, an improved method based on variable switching region and linear region is proposed. The stability proof is given. The simulation results show that the proposed control strategy can enhance the dynamic performance of the EMA position servo and its disturbance rejection ability.
-
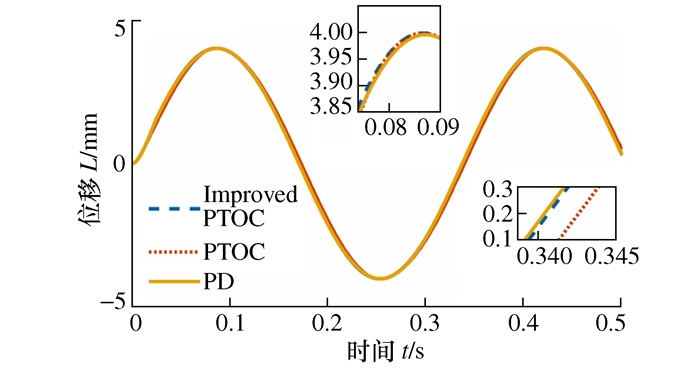
表 1 10 Nm负载时20 mm阶跃响应对比
控制律 超调量/% 95%调节时间/ms Improved PTOC 0 229 Original PTOC[11] 8.5 222 PD 0.8 225 -
[1] ZHOU Y, ZHOU H, LOU J Y, et al. EMA servo control system based on PMSM[C]//Proceedings of 2020 Chinese Control and Decision Conference. Hefei, China: IEEE, 2020: 155-160 [2] GIANGRANDE P, GALASSINI A, PAPADOPOULOS S, et al. Considerations on the development of an electric drive for a secondary flight control electromechanical actuator[J]. IEEE Transactions on Industry Applications, 2019, 55(4): 3544-3554 doi: 10.1109/TIA.2019.2907231 [3] 万琦, 刘更, 乔冠, 等. 机电作动器舵回路系统动态特性分析[J]. 机械科学与技术, 2017, 36(5): 805-810 doi: 10.13433/j.cnki.1003-8728.2017.0524WAN Q, LIU G, QIAO G, et al. Analyzing dynamic characteristics of rudder loop system for an electro-mechanical actuator[J]. Mechanical Science and Technology for Aerospace Engineering, 2017, 36(5): 805-810 (in Chinese) doi: 10.13433/j.cnki.1003-8728.2017.0524 [4] CHEN S Y, LIU T S. Intelligent tracking control of a PMLSM using self-evolving probabilistic fuzzy neural network[J]. IET Electric Power Applications, 2017, 11(6): 1043-1054 doi: 10.1049/iet-epa.2016.0819 [5] DENG Y T, WANG J L, LI H W, et al. Adaptive sliding mode current control with sliding mode disturbance observer for PMSM drives[J]. ISA Transactions, 2019, 88: 113-126 doi: 10.1016/j.isatra.2018.11.039 [6] LIU C Q, LUO G Z, CHEN Z, et al. A linear ADRC-based robust high-dynamic double-loop servo system for aircraft electro-mechanical actuators[J]. Chinese Journal of Aeronautics, 2019, 32(9): 2174-2187 doi: 10.1016/j.cja.2019.03.036 [7] 王立俊, 赵吉文, 董菲, 等. 基于自适应内模观测器的永磁同步直线电机高带宽强鲁棒预测电流控制策略研究[J]. 中国电机工程学报, 2019, 39(10): 3098-3106 https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201910030.htmWANG L J, ZHAO J W, DONG F, et al. High-bandwidth and strong robust predictive current control strategy research for permanent-magnet synchronous linear motor based on adaptive internal model observer[J]. Proceedings of the CSEE, 2019, 39(10): 3098-3106 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201910030.htm [8] 程国卿, 胡金高. 限速伺服系统的近似时间最优控制方案[J]. 西安电子科技大学学报, 2015, 42(1): 180-186 doi: 10.3969/j.issn.1001-2400.2015.01.029CHENG G Q, HU J G. Proximate time-optimal control scheme for speed-constrained servo systems[J]. Journal of Xidian University, 2015, 42(1): 180-186 (in Chinese) doi: 10.3969/j.issn.1001-2400.2015.01.029 [9] 邱攀峰, 钟钦洪, 胡勤丰, 等. 定点位置伺服系统的近似时间最优控制[J]. 微电机, 2018, 51(1): 59-64 https://www.cnki.com.cn/Article/CJFDTOTAL-WDJZ201801012.htmQIU P F, ZHONG Q H, HU Q F, et al. Proximate time-optimal servomechanisms control for set-point position servo system[J]. Micromotors, 2018, 51(1): 59-64 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WDJZ201801012.htm [10] 周成锋. EMA数字伺服控制系统研究[D]. 南京: 南京航空航天大学, 2013ZHOU C F. Research on EMA digital servo control system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013 (in Chinese) [11] GAO Z Q. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the 2003 American Control Conference, 2003. Denver: IEEE, 2003: 4989-4996 [12] 杨赟杰, 朱纪洪, 和阳. 近似时间最优的舵机多模位置控制策略[J]. 控制理论与应用, 2018, 35(4): 468-474 https://www.cnki.com.cn/Article/CJFDTOTAL-KZLY201804006.htmYANG Y J, ZHU J H, HE Y. Multi-mode position control strategy with approximate time-optimal for actuator[J]. Control Theory & Applications, 2018, 35(4): 468-474 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KZLY201804006.htm [13] DHANDA A, FRANKLIN G F. An improved 2-DOF proximate time optimal servomechanism[J]. IEEE Transactions on Magnetics, 2009, 45(5): 2151-2164 doi: 10.1109/TMAG.2009.2013247 [14] 胡金高, 程国扬. 鲁棒近似时间最优控制及其在电机伺服系统的应用[J]. 电工技术学报, 2014, 29(7): 163-172 https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS201407022.htmHU J G, CHENG G Y. Robust proximate time-optimal control with application to a motor servo system[J]. Transactions of China Electrotechnical Society, 2014, 29(7): 163-172 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS201407022.htm [15] WORKMAN M L, KOSUT R L, FRANKLIN G F. Adaptive proximate time-optimal servomechanisms: continuous time case[C]//Proceedings of 1987 American Control Conference. Minneapolis: IEEE, 1987: 589-594 -







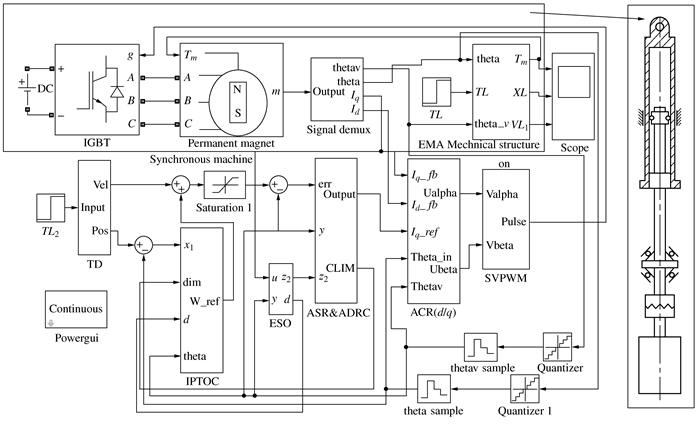
 下载:
下载: