Application of VMD-SVD in Underdetermined Source Number Estimation of Mechanical Fault Signals
-
摘要: 针对在观测信号数目小于机械故障振动信号源数目的欠定情况下, 源信号的个数难以估计的问题, 提出一种变分模态分解(Variational mode decomposition, VMD)和奇异值分解(Singular value decomposition, SVD)相结合的盲源数目估计方法。首先利用VMD对振动信号进行分解, 得到若干本征模态函数分量(Intrinsic mode function, IMF), 然后对IMF进行重新组合得到多维观测信号的协方差矩阵, 最后依据奇异值分解的结果来对信号源数目进行最终确定。仿真信号分析验证了该方法的有效性, 将该方法运用到轴承复合故障振动信号中, 分析结果表明, 该方法能够实现欠定情况下源数目的可靠估计。Abstract: To solve the problem that it is difficult to estimate the number of source signals when the number of observed signals is less than the number of vibration signal sources for mechanical faults, a blind source number estimation method based on variational mode decomposition (VMD) and singular value decomposition (SVD) was proposed in this paper. Firstly, VMD was used to decompose the original vibration signal to obtain several intrinsic mode function (IMF). Then, IMF was recombined to obtain the covariance matrix of multidimensional observation signals. Finally, the number of signal sources was determined according to the result of singular value decomposition. Simulation signal analysis verifies the effectiveness of the method. And the method is also applied to the vibration signals of the bearing composite faults, and the analysis results show that the method can achieve reliable estimation of the number of sources under underdetermined conditions.
-
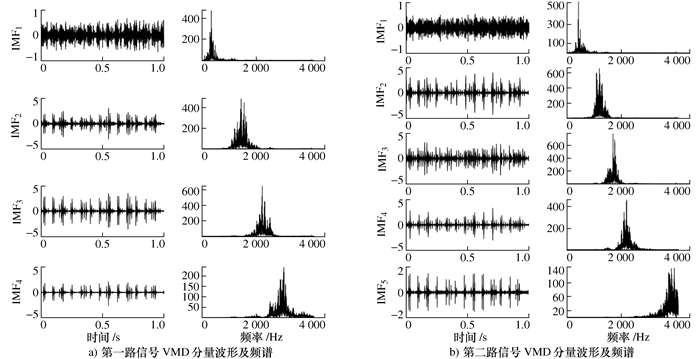
表 1 第一路信号不同K值所对应的中心频率
K1 中心频率/Hz IMF1 IMF2 IMF3 IMF4 IMF5 IMF6 IMF7 2 463 2 231 3 365 1 456 2 283 4 363 1 448 2 235 2 944 5 356 1 300 1 596 2 247 2 953 6 356 1 294 1 590 2 239 2 909 3 775 表 2 第二路信号不同K值所对应的中心频率
K2 中心频率/Hz IMF1 IMF2 IMF3 IMF4 IMF5 IMF6 IMF7 2 1 201 1 753 4 470 1 196 1 716 2 183 5 469 1 196 1 715 2 180 3 821 6 459 1 154 1 462 1 754 2 192 3 823 7 459 1 154 1 461 1 752 2 181 3 002 3 846 表 3 奇异值分解相关结果
名称 σ1 σ2 σ3 σ4 σ5 σ6 σ7 σ8 σ9 特征值 0.360 5 0.280 1 0.235 3 0.141 3 0.090 9 0.061 8 0.042 1 0.036 1 0.029 8 邻近比 1.287 0 1.190 4 1.665 3 1.554 5 1.470 9 1.468 0 1.166 2 1.211 4 -
[1] KEMIHA M, KACHA A. Complex blind source separation[J]. Circuits, Systems, and Signal Processing, 2017, 36(11): 4670-4687 doi: 10.1007/s00034-017-0539-0 [2] 毋文峰, 陈小虎, 苏勋家, 等. 机械振动源数估计的小波方法[J]. 机械科学与技术, 2011, 30(10): 1679-1682 https://www.cnki.com.cn/Article/CJFDTOTAL-JXKX201110018.htmWU W F, CHEN X H, SU X J, et al. Wavelet decomposition algorithm for source number estimation of mechanical vibration[J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 30(10): 1679-1682 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXKX201110018.htm [3] 潘高元, 李舜酩, 杜华蓉, 等. 齿轮箱断齿特征识别的S变换-SVD降噪组合方法[J]. 振动与冲击, 2019, 38(18): 256-263 https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201918036.htmPAN G Y, LI S M, DU H R, et al. Feature extracting method for gearbox tooth breakage under impact based on the S-transform time-frequency spectrum combined with the denoising by SVD[J]. Journal of Vibration and Shock, 2019, 38(18): 256-263 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201918036.htm [4] 谭北海, 谢胜利. 基于源信号数目估计的欠定盲分离[J]. 电子与信息学报, 2008, 30(4): 863-867 https://www.cnki.com.cn/Article/CJFDTOTAL-DZYX200804026.htmTAN B H, XIE S L. Underdetermined blind separation based on source signals' number estimation[J]. Journal of Electronics & Information Technology, 2008, 30(4): 863-867 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZYX200804026.htm [5] 周俊, 伍星, 迟毅林, 等. 盲解卷积和频域压缩感知在轴承复合故障声学诊断的应用[J]. 机械工程学报, 2016, 52(3): 63-70 https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201603010.htmZHOU J, WU X, CHI Y L, et al. Blind deconvolution and frequency domain compressive sensing application in bearing composite acoustic fault diagnosis[J]. Journal of Mechanical Engineering, 2016, 52(3): 63-70 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201603010.htm [6] GILLES J. Empirical wavelet transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010 doi: 10.1109/TSP.2013.2265222 [7] DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544 doi: 10.1109/TSP.2013.2288675 [8] 赵昕海, 张术臣, 李志深, 等. 基于VMD的故障特征信号提取方法[J]. 振动、测试与诊断, 2018, 38(1): 11-19, 202 https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCS201801002.htmZHAO X H, ZHANG S C, LI Z S, et al. Application of new denoising method based on VMD in fault feature extraction[J]. Journal of Vibration, Measurement & Diagnosis, 2018, 38(1): 11-19, 202 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCS201801002.htm [9] 刘长良, 武英杰, 甄成刚. 基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J]. 中国电机工程学报, 2015, 35(13): 3358-3365 https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201513023.htmLIU C L, WU Y J, ZHEN C G. Rolling bearing fault diagnosis based on variational mode decomposition and fuzzy C means clustering[J]. Proceedings of the CSEE, 2015, 35(13): 3358-3365 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201513023.htm [10] ZHOU Y N, ZHANG Y, YANG D D, et al. Pipeline signal feature extraction with improved VMD and multi-feature fusion[J]. Systems Science & Control Engineering, 2020, 8(1): 318-327 doi: 10.1080/21642583.2020.1765218 [11] ZHANG X, MIAO Q, ZHANG H, et al. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery[J]. Mechanical Systems and Signal Processing, 2018, 108: 58-72 doi: 10.1016/j.ymssp.2017.11.029 [12] 姜万录, 雷亚飞, 韩可, 等. 基于VMD和SVDD结合的滚动轴承性能退化程度定量评估[J]. 振动与冲击, 2018, 37(22): 43-50 https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201822007.htmJIANG W L, LEI Y F, HAN K, et al. Performance degradation quantitative assessment method for rolling bearings based on VMD and SVDD[J]. Journal of Vibration and Shock, 2018, 37(22): 43-50 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201822007.htm [13] GOLAFSHAN R, SANLITURK K Y. SVD and Hankel matrix based de-noising approach for ball bearing fault detection and its assessment using artificial faults[J]. Mechanical Systems and Signal Processing, 2016, 70-71: 36-50 doi: 10.1016/j.ymssp.2015.08.012 [14] 付强, 景博, 何鹏举, 等. 动态信号源数目盲估计方法研究[J]. 仪器仪表学报, 2020, 41(4): 119-128 https://www.cnki.com.cn/Article/CJFDTOTAL-YQXB202004014.htmFU Q, JING B, HE P J, et al. Research on dynamic signal source number blind estimation method[J]. Chinese Journal of Scientific Instrument, 2020, 41(4): 119-128 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YQXB202004014.htm [15] 叶红仙, 杨世锡, 杨将新. 基于EMD-SVD-BIC的机械振动源数估计方法[J]. 振动、测试与诊断, 2010, 30(3): 330-334 doi: 10.3969/j.issn.1004-6801.2010.03.026YE H X, YANG S X, YANG J X. Mechanical vibration source number estimation based on EMD-SVD-BIC[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(3): 330-334 (in Chinese) doi: 10.3969/j.issn.1004-6801.2010.03.026 -








 下载:
下载: