Advance in Impact Force Model Research with Evolution of Newton Restitution Coefficient
-
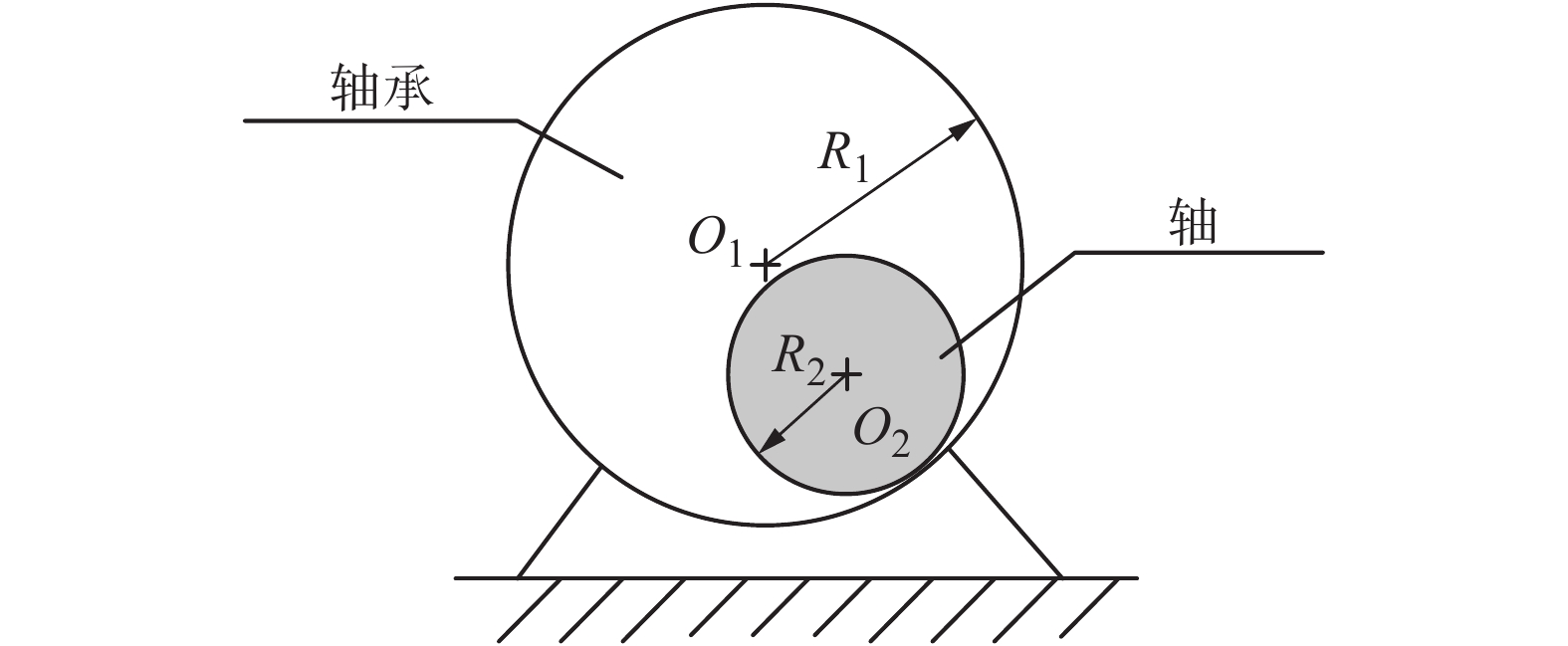
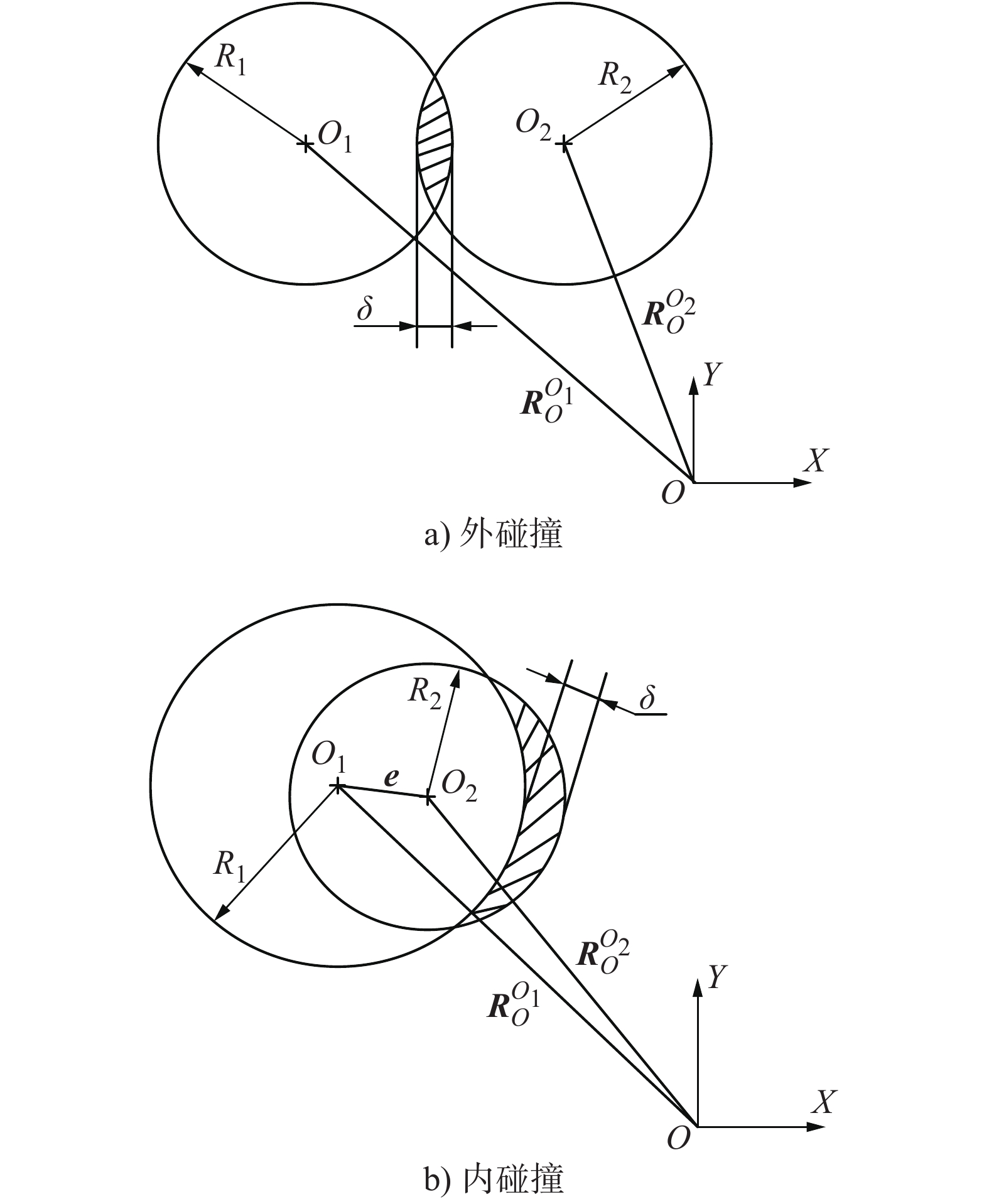
摘要: 为了辨识间隙铰链处碰撞力的适用范围,更加准确地描述机械系统中普遍存在的碰撞现象及其对机械系统动态特性的影响规律,以牛顿碰撞恢复系数作为评价指标,以间隙铰链处轴、轴承间的碰撞和恢复过程为例,在不同恢复系数下和碰撞力模型下进行数值模拟及对比分析。研究发现,不同碰撞恢复系数下各模型碰撞过程的最大碰撞力、最大变形量及实际碰撞恢复系数差异较大。因此,实际选择碰撞力模型时应依据碰撞初始条件和材料特性等进行综合考虑。Abstract: In order to identify the application scope of impact force models in clearance joint, and more accurately describe the collision phenomenon in mechanical system, the Newton restitution coefficient is defined as evaluation index, and the joint of journal-bearing is used as example. Then a great number of numerical results are presented based on different impact force models with different coefficient of restitution. It can be concluded that the maximum value of impact force and deformation, as well as actual restitution have obvious difference for different impact forces, so the selection of impact force model should be considered comprehensively with initial collision conditions and material properties.
-
Key words:
- clearance joint /
- collision /
- impact force model /
- Newton restitution coefficient
-
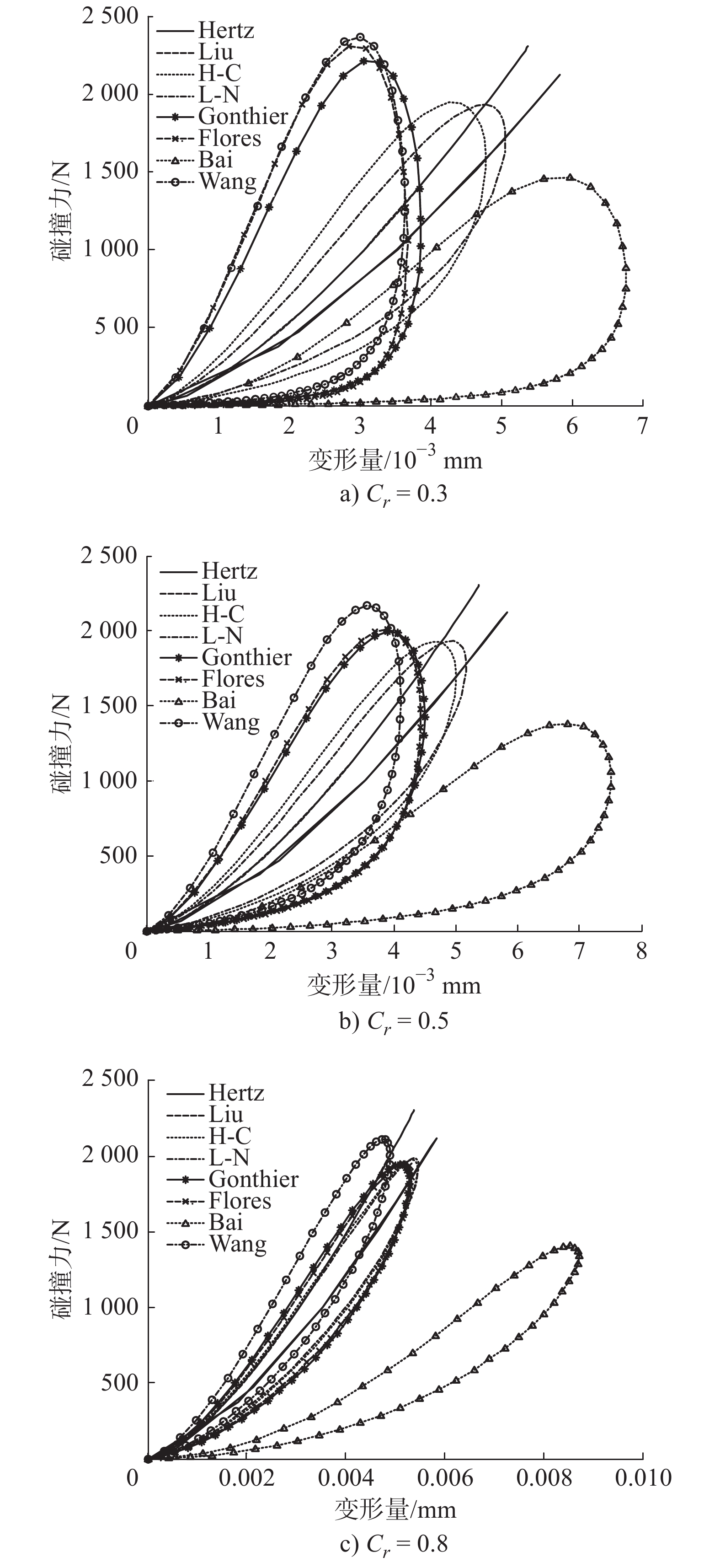
表 1 不同碰撞力模型在3种恢复系数值下的最大碰撞力
碰撞力模型 最大碰撞力/N Cr = 0.3 Cr = 0.5 Cr = 0.8 Hertz 2136.033 2136.033 2136.033 Liu 2305.168 2305.168 2305.168 H-C 1943.499 1929.073 1975.844 L-N 1928.888 1933.646 1986.405 Gonthier 2207.553 1993.206 1945.774 Flores 2308.516 2006.623 1952.949 Bai 1459.471 1382.348 1405.777 Wang 2362.823 2166.395 2111.053 表 2 不同碰撞力模型在3种恢复系数值下的最大变形量
碰撞力模型 最大变形量/mm Cr = 0.3 Cr = 0.5 Cr = 0.8 Hertz 0.00585 0.00585 0.00585 Liu 0.00538 0.00538 0.00538 H-C 0.00478 0.00500 0.00545 L-N 0.00506 0.00517 0.00548 Gonthier 0.00387 0.00450 0.00528 Flores 0.00368 0.00444 0.00534 Bai 0.00677 0.00752 0.00871 Wang 0.00363 0.00412 0.00490 表 3 Cr = 0.3时不同碰撞力模型实际恢复系数及相对误差
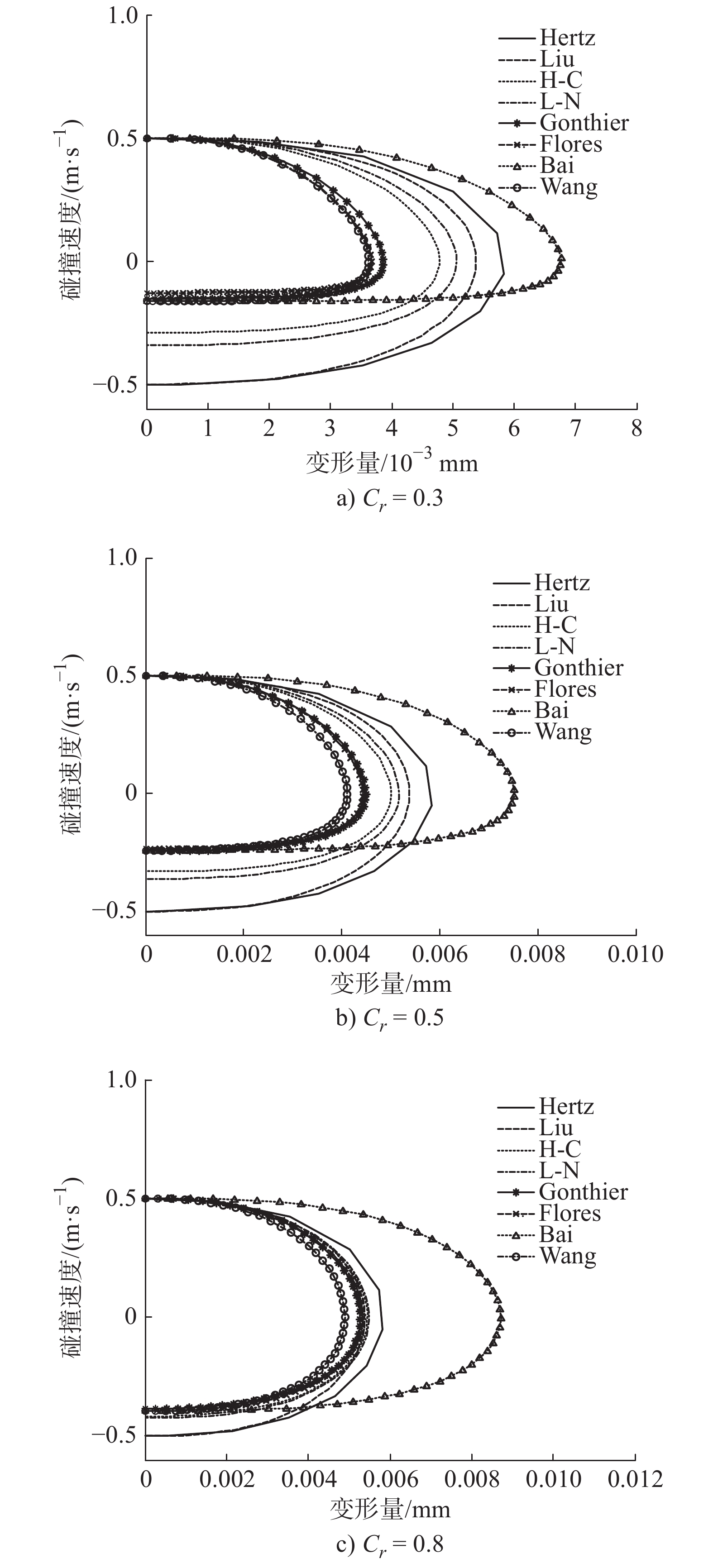
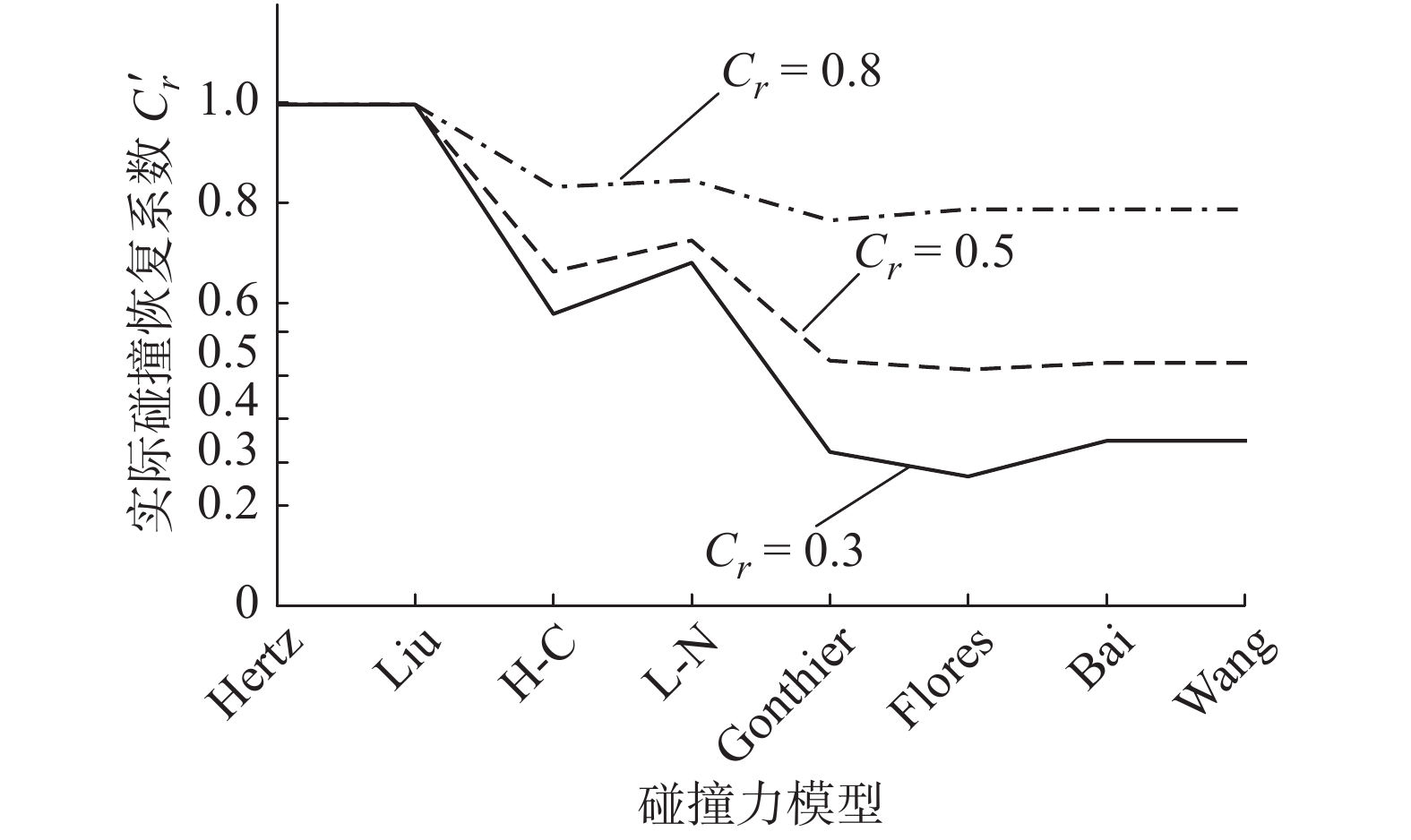
碰撞力模型 初始速度/
(m·s−1)分离速度/(m·s−1) 实际恢复系数及误差 Cr′ 误差/% Hertz 0.5 0.5 1 0 Liu 0.5 0.5 1 0 H-C 0.5 −0.2906 0.5812 93.7333 L-N 0.5 −0.3421 0.6842 128.0667 Gonthier 0.5 −0.1521 0.3042 1.4 Flores 0.5 −0.1281 0.2562 14.6 Bai 0.5 −0.1634 0.3268 8.9333 Wang 0.5 −0.1634 0.3268 8.9333 表 4 Cr = 0.5时不同碰撞力模型实际恢复系数及相对误差
碰撞力模型 初始速度/
(m·s−1)分离速度/
(m·s−1)实际恢复系数及误差 Cr′ 误差/% Hertz 0.5 0.5 1 0 Liu 0.5 0.5 1 0 H-C 0.5 −0.3315 0.663 24.585 L-N 0.5 −0.3626 0.7252 31.054 Gonthier 0.5 −0.2439 0.4878 2.501 Flores 0.5 −0.2352 0.4704 6.293 Bai 0.5 −0.2413 0.4826 3.605 Wang 0.5 −0.2413 0.4826 3.605 表 5 Cr = 0.8时不同碰撞力模型恢复系数及对应相对误差
碰撞力模型 初始速度(m·s−1) 分离速度(m·s−1) 实际恢复系数及误差 Cr′ 误差/% Hertz 0.5 0.5 1 0 Liu 0.5 0.5 1 0 H-C 0.5 −0.4164 0.8328 4.1 L-N 0.5 −0.4236 0.8472 5.9 Gonthier 0.5 −0.384 0.768 4 Flores 0.5 −0.3943 0.7886 1.425 Bai 0.5 −0.3937 0.7874 1.575 Wang 0.5 −0.3937 0.7874 1.575 -
[1] Flores P, Ambrósio J, Claro J C P, et al. A study on dynamics of mechanical systems including joints with clearance and lubrication[J]. Mechanism and Machine Theory, 2006, 41(3): 247-261 doi: 10.1016/j.mechmachtheory.2005.10.002 [2] Erkaya S. Prediction of vibration characteristics of a planar mechanism having imperfect joints using neural network[J]. Journal of Mechanical Science and Technology, 2012, 26(5): 1419-1430 doi: 10.1007/s12206-012-0308-8 [3] Wang X P, Lin W Z, Ji X M, et al. Dynamic analysis of a planar multibody system with multiple revolute clearance joints[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2019, 233(10): 3429-3443 doi: 10.1177/0954406218819022 [4] Wang X P, Zhang Y, Gao Z, et al. Modeling and analysis of impact based on numerical and experimental approaches[J]. Advances in Mechanical Engineering, 2018, 10(12): 1-13 [5] Nurre G S, Sharkey J P, Nelson J D, et al. Preservicing mission - on-orbit modifications to hubble space telescope pointing control system[J]. Journal of Guidance, Control, and Dynamic, 1995, 18(2): 222-229 doi: 10.2514/3.21373 [6] 姚文莉, 岳嵘. 有争议的碰撞恢复系数研究进展[J]. 振动与冲击, 2015, 34(19): 43-48Yao W L, Yue R. Advance in controversial restitution coefficient study for impact problems[J]. Journal of Vibration and Shock, 2015, 34(19): 43-48 (in Chinese [7] Newton I. Philosophiae naturalis principia mathematica[M]. Apud. Guil. & Joh. Innys, 1726 [8] Kilmister C W, Reeve J E. Rational mechanics [M]. Upper Saddle River, NJ: Prentice Hall Press, 1966 [9] Stronge W J. Theoretical coefficient of restitution for planer impact of rough elasto-plastic bodies[R]. CONF-950686-TRN: 95: 006111-0385, 1995, 205: 351-362. [10] 王旭鹏, 张艳, 吉晓民, 等. 一种基于变恢复系数的接触碰撞力模型[J]. 振动与冲击, 2019, 38(5): 198-202Wang X P, Zhang Y, Ji X M, et al. A contact-impact force model based on variable recovery coefficient[J]. Journal of Vibration and Shock, 2019, 38(5): 198-202 (in Chinese [11] Hertz H. Über dies Berührung fester elasticher Körper[J]. Journal Reine und Angewandte Mathematik, 1881(92): 156-171 [12] Liu C S, Zhang K, Yang L. The compliance contact model of cylindrical joints with clearances[J]. Acta Mechanica Sinica, 2005, 21(5): 451-458 doi: 10.1007/s10409-005-0061-7 [13] Liu C S, Zhang K, Yang R. The FEM analysis and approximate model for cylindrical joints with clearances[J]. Mechanism and Machine Theory, 2007, 42(2): 183-197 doi: 10.1016/j.mechmachtheory.2006.02.006 [14] Tian Q, Liu C, Machado M, et al. A new model for dry and lubricated cylindrical joints with clearance in spatial flexible multibody systems[J]. Nonlinear Dynamics, 2011, 64(1): 25-47 [15] 王旭鹏. 含间隙铰链机构非线性接触力和碰撞动力学研究[D]. 西安: 西北工业大学, 2016.Wang X P. Research on nonlinear contact forces and impact dynamics of mechanism with clearance joints[D]. Xi′an: Northwestern Polytechnical University, 2016 (in Chinese). [16] Goldsmith W. Impact-the theory and physical behaviour of colliding solids[M]. London, England: Edward Arnold Ltd., 1960. [17] Machado M, Moreira P, Flores P, et al. Compliant contact force models in multibody dynamics: Evolution of the Hertz contact theory[J]. Mechanism and Machine Theory, 2012, 53: 99-121 doi: 10.1016/j.mechmachtheory.2012.02.010 [18] Hunt K H, Crossley F R E. Coefficient of restitution interpreted as damping in vibroimpact[J]. Journal of Applied Mechanics, 1975, 42(2): 440-445 doi: 10.1115/1.3423596 [19] Lankarani H M, Nikravesh P E. A contact force model with hysteresis damping for impact analysis of multibody systems[J]. Journal of Mechanical Design, 1990, 112(3): 369-376 doi: 10.1115/1.2912617 [20] Gonthier Y, McPhee J, Lange C, Piedboeuf J C. A regularized contact model with asymmetric damping and dwell-time dependent friction[J]. Multibody system dynamics, 2004, 11: 209-233. [21] 秦志英, 陆启韶. 基于恢复系数的碰撞过程模型分析[J]. 动力学与控制学报, 2006, 4(4): 294-298Qin Z Y, Lu Q S. Analysis of impact process model based on restitution coefficien[J]. Journal of Dynamics and Control, 2006, 4(4): 294-298 (in Chinese [22] Flores P, Machado M, Silva M T, et al. On the continuous contact force models for soft materials in multibody dynamics[J]. Multibody System Dynamics, 2011, 25(3): 357-375 doi: 10.1007/s11044-010-9237-4 [23] Flores P, Koshy C S, Lankarani H M, et al. Numerical and experimental investigation on multibody systems with revolute clearance joints[J]. Nonlinear Dynamics, 2011, 65(4): 383-398 doi: 10.1007/s11071-010-9899-8 [24] Flores P, Lankarani H M. Dynamic response of multibody systems with multiple clearance joints[J]. Journal of Computational and Nonlinear Dynamics, 2012, 7(3): 031003 doi: 10.1115/1.4005927 [25] Koshy C S, Flores P, Lankarani H M. Study of the effect of contact force model on the dynamic response of mechanical systems with dry clearance joints: computational and experimental approaches[J]. Nonlinear Dynamics, 2013, 73(1-2): 325-338 doi: 10.1007/s11071-013-0787-x [26] Machado M, Costa J, Seabra E, et al. The effect of the lubricated revolute joint parameters and hydrodynamic force models on the dynamic response of planar multibody systems[J]. Nonlinear Dynamics, 2012, 69(1-2): 635-654 doi: 10.1007/s11071-011-0293-y [27] 王旭鹏, 刘更, 马尚君. 含间隙运动副机构的动力学特性研究[J]. 振动与冲击, 2016, 35(7): 110-115Wang X P, Liu G, Ma S J. Dynamic characteristics of mechanisms with revolute clearance joints[J]. Journal of Vibration and Shock, 2016, 35(7): 110-115 (in Chinese [28] 白争锋. 考虑铰间间隙的机构动力学特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2011.Bai Z F. Research on dynamic characteristics of mechanism with joint clearance[D]. Harbin: Harbin Institute of Technology, 2011 (in Chinese). [29] Bai Z F, Zhao Y. Dynamic behaviour analysis of planar mechanical systems with clearance in revolute joints using a new hybrid contact force model[J]. International Journal of Mechanical Sciences, 2012, 54(1): 190-205 doi: 10.1016/j.ijmecsci.2011.10.009 [30] Bai Z F, Zhao Y. Dynamics modeling and quantitative analysis of multibody systems including revolute clearance joint[J]. Precision Engineering, 2012, 36(4): 554-567 doi: 10.1016/j.precisioneng.2012.04.002 [31] Bai Z F, Zhao Y. A hybrid contact force model of revolute joint with clearance for planar mechanical systems[J]. International Journal of Non-Linear Mechanics, 2013, 48: 15-36 doi: 10.1016/j.ijnonlinmec.2012.07.003 [32] 白争锋, 赵阳, 赵志刚. 考虑运动副间隙的机构动态特性研究[J]. 振动与冲击, 2011, 30(11): 17-20, 41Bai Z F, Zhao Y, Zhao Z G. Dynamic characteristics of mechanisms with joint clearance[J]. Journal of Vibration and Shock, 2011, 30(11): 17-20, 41 (in Chinese [33] Bai Z F, Zhao Y. Research on dynamic wear of revolution joint with clearance for mechanical system[J]. Applied Mechanics and Materials, 2011, 55-57: 488-493 doi: 10.4028/www.scientific.net/AMM.55-57.488 [34] 王旭鹏, 刘更, 马尚君, 等. 间隙铰链对平面机构碰撞动力学特性影响分析[J]. 振动与冲击, 2017, 36(17): 74-78Wang X P, Liu G, Ma S J, et al. Effects of clearance joint on impact dynamic characteristics of planar mechanisms[J]. Journal of Vibration and Shock, 2017, 36(17): 74-78 (in Chinese [35] Wang X P, Liu G, Ma S J. Dynamic analysis of planar mechanical systems with clearance joints using a new nonlinear contact force model[J]. Journal of Mechanical Science and Technology, 2016, 30(4): 1537-1545 doi: 10.1007/s12206-016-0308-1 [36] Wang X P, Liu G. Modeling and simulation of revolute joint with clearance in planar multi-body systems[J]. Journal of Mechanical Science and Technology, 2015, 29(10): 4113-4120 doi: 10.1007/s12206-015-0905-4 [37] Wang X P, Liu G, Ma S J, et al. Study on dynamic responses of planar multibody systems with dry revolute clearance joint: Numerical and experimental approaches[J]. Journal of Sound and Vibration, 2019, 438: 116-138 doi: 10.1016/j.jsv.2018.08.052 [38] Xu B C, Wang X P, Ji X M, et al. Dynamic and motion consistency analysis for a planar parallel mechanism with revolute dry clearance joints[J]. Journal of Mechanical Science and Technology, 2017, 31(7): 3199-3209 doi: 10.1007/s12206-017-0609-z [39] Lee T W, Wang A C. On the dynamics of intermittent-motion mechanisms. Part 1: dynamic model and response[J]. Journal of Mechanisms, Transmissions, and Automation in Design, 1983, 105(3): 534-540 doi: 10.1115/1.3267392 [40] Herbert R G, McWhannell D C. Shape and frequency composition of pulses from an impact pair[J]. Journal of Engineering for Industry, 1977, 99(3): 513-518 doi: 10.1115/1.3439270 [41] Anagnostopoulos A S. Pounding of buildings in series during earthquakes[J]. Earthquake Engineering and Structural Dynamics, 1988, 16(3): 443-456 doi: 10.1002/eqe.4290160311 [42] Tsuji Y, Tanaka T, Ishida T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe[J]. Powder Technology, 1992, 71(3): 239-250 doi: 10.1016/0032-5910(92)88030-L [43] Brilliantov N V, Spahn F, Hertzsch J M, et al. The collision of particles in granular systems[J]. Physica A: Statistical Mechanics and its Applications, 1996, 231(4): 417-424 doi: 10.1016/0378-4371(96)00099-4 [44] Hu S W, Guo X L. A dissipative contact force model for impact analysis in multibody dynamics[J]. Multibody System Dynamics, 2015, 35(2): 131-151 doi: 10.1007/s11044-015-9453-z [45] Yigit A S, Christoforou A P, Majeed M A. A nonlinear visco-elastoplastic impact model and the coefficient of restitution[J]. Nonlinear Dynamics, 2011, 66(4): 509-521 doi: 10.1007/s11071-010-9929-6 [46] Thornton C. Coefficient of restitution for collinear collisions of elastic-perfectly plastic spheres[J]. Journal of Applied Mechanics, 1997, 64(2): 383-386 doi: 10.1115/1.2787319 [47] Kagami J, Yamada K, Hatazawa T. Contact between a sphere and rough plates[J]. Wear, 1983, 87(1): 93-105 doi: 10.1016/0043-1648(83)90025-X [48] Wu C Y, Li L Y, Thornton C. Energy dissipation during normal impact of elastic and elastic-plastic spheres[J]. International Journal of Impact Engineering, 2005, 32(1-4): 593-604 doi: 10.1016/j.ijimpeng.2005.08.007 [49] Burgin L V, Aspden R M. Impact testing to determine the mechanical properties of articular cartilage in isolation and on bone[J]. Journal of Materials Science: Materials in Medicine, 2008, 19(2): 703-711 doi: 10.1007/s10856-007-3187-2 [50] Shi X, Polycarpou A A. Measurement and modeling of normal contact stiffness and contact damping at the meso scale[J]. Journal of Vibration and Acoustics, 2005, 127(1): 52-60 doi: 10.1115/1.1857920 -







 下载:
下载: