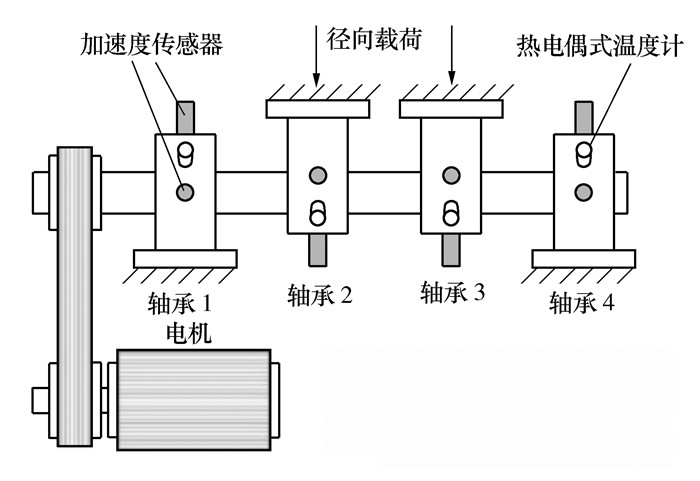
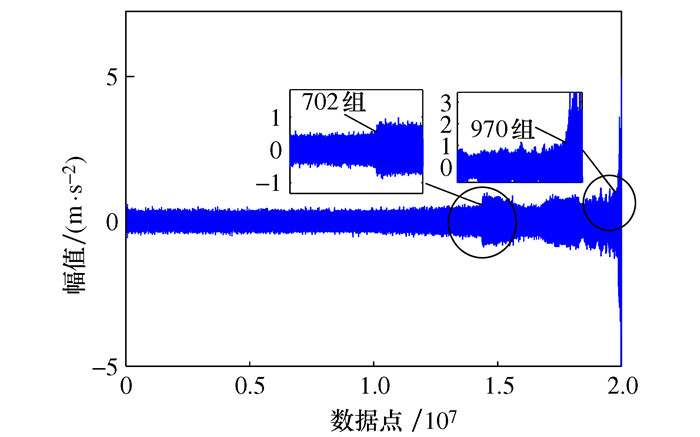
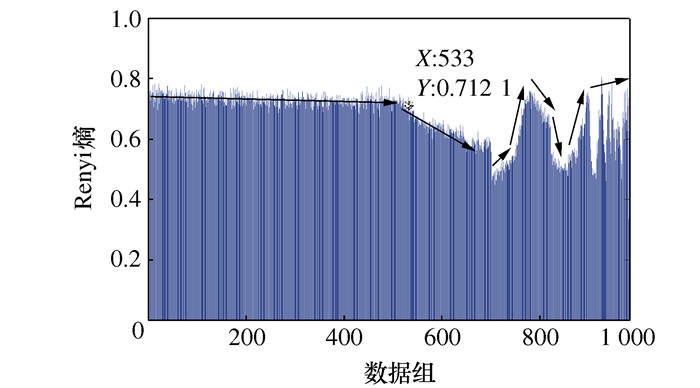
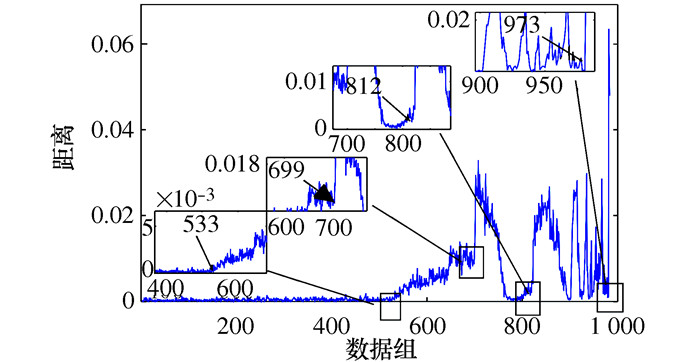
Application of HDLMD and JRD in Performance Evaluation of Rolling Bearing
-
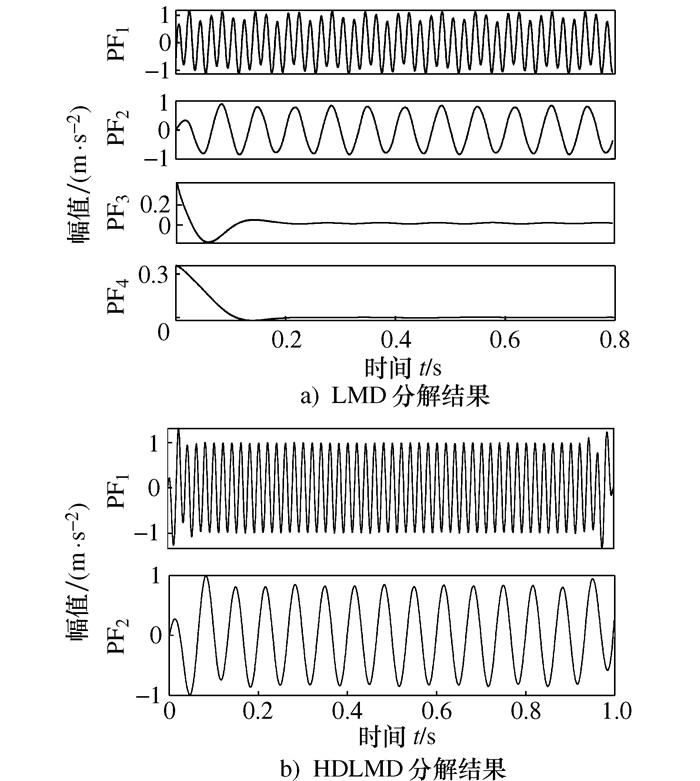
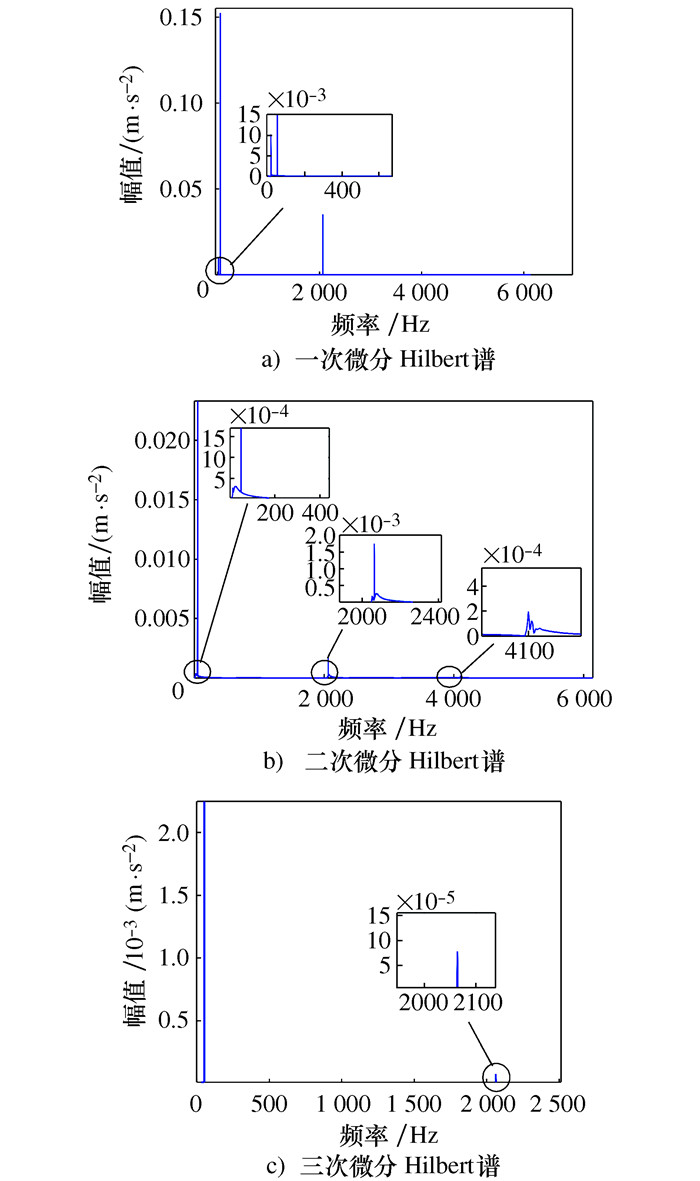
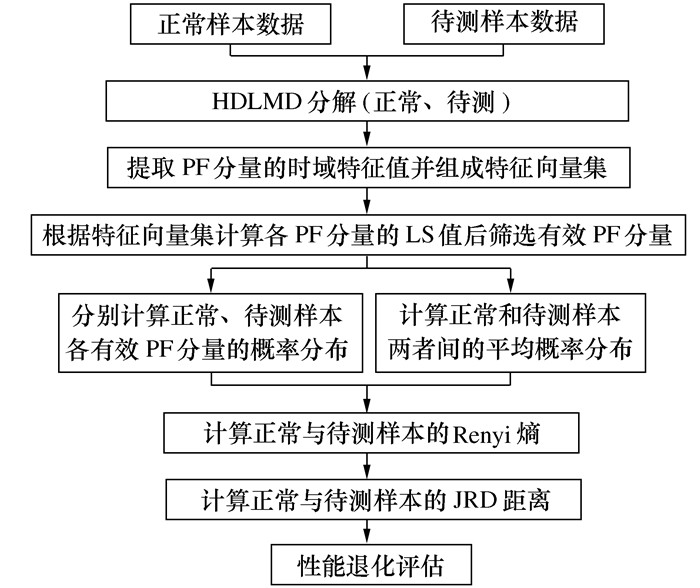
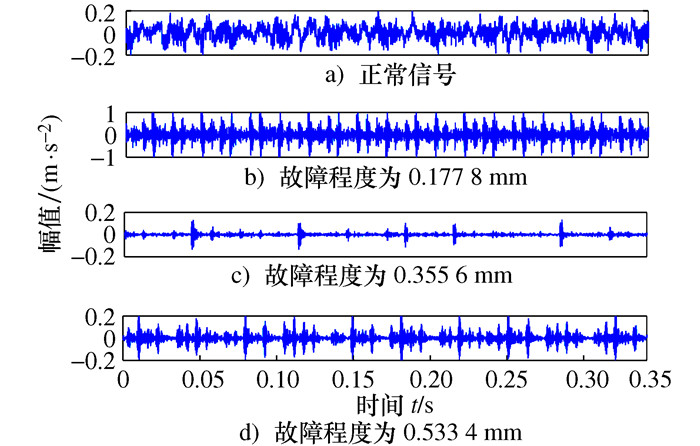
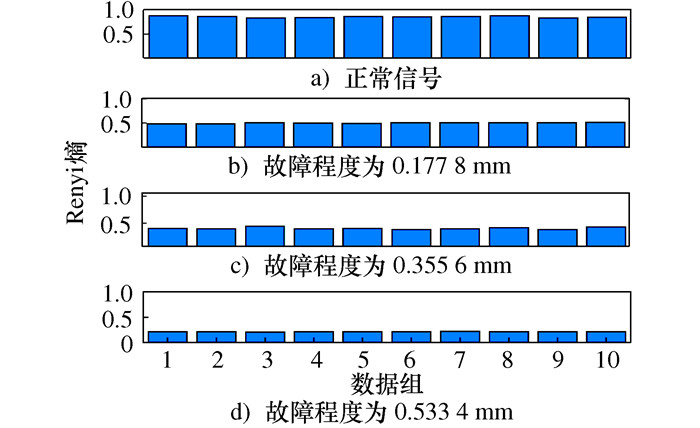
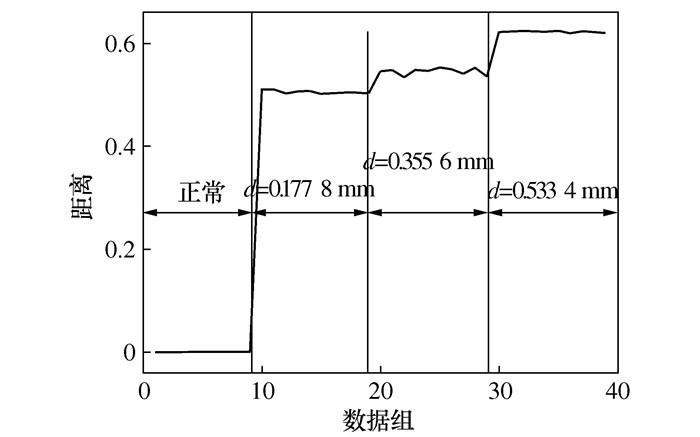
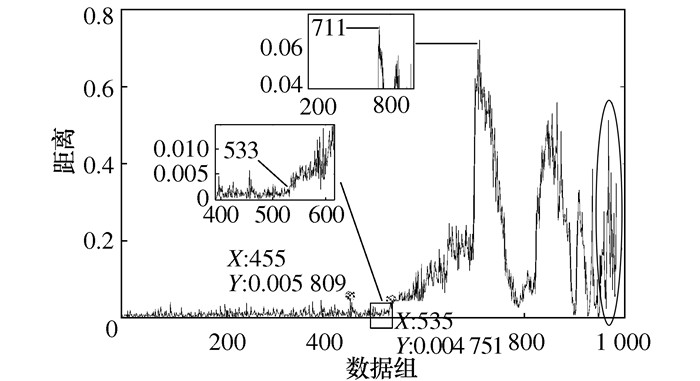
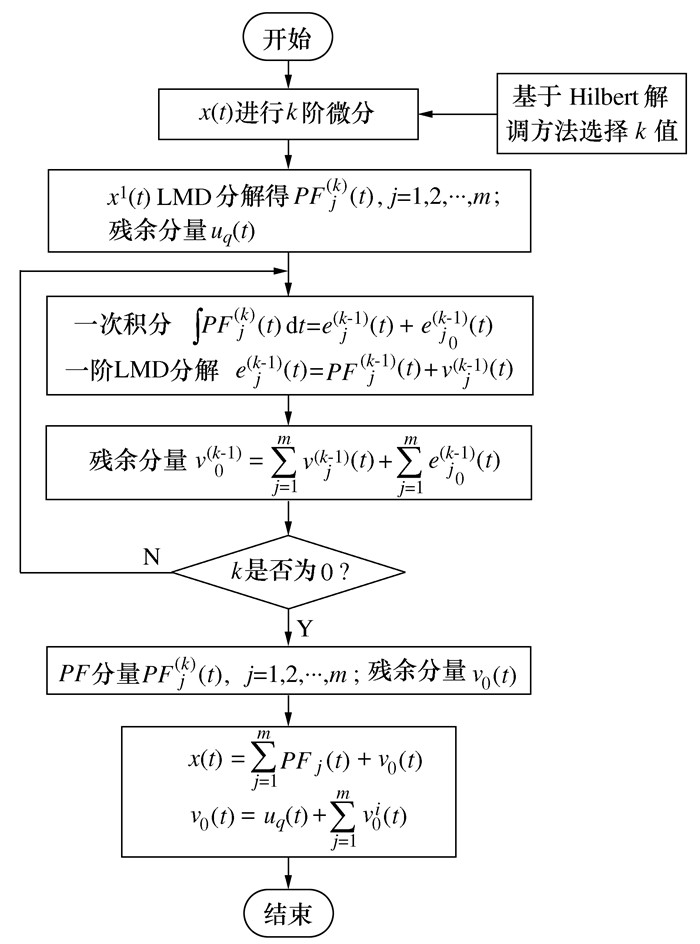
摘要: 针对微分局部均值分解(Differential local mean decomposition, DLMD)方法中微分次数计算缺乏理论指导以及传统性能退化指标无法准确表示滚动轴承在全寿命阶段上当前状态的问题, 提出了一种基于HDLMD(Hilbert-differential local mean decomposition, HDLMD)和JRD(Jensen-Renyi divergence)的滚动轴承性能评估方法。该方法首先对原始振动信号进行HDLMD分解, 提取乘积函数(Product function, PF)矩阵; 然后, 基于拉普拉斯分值(Laplacian score, LS)选择包含最多故障信息的PF分量; 再计算筛选之后的有效PF分量的概率分布, 得到有效PF分量的Renyi熵值; 最后, 计算正常信号与不同故障程度信号之间的JRD距离, 并判断滚动轴承的退化状态。通过凯西斯储大学(Case western reserve university, CWRU)滚动轴承实验数据和NASA(National aeronautics and space administration)全寿命周期数据实验表明, 本文所提方法可以准确、有效地评估轴承性能的退化状态。Abstract: Due to the lack of theoretical guidance in differential local mean decomposition (DLMD) method and the inability of traditional performance degradation index to accurately represent the current state of rolling bearing in the whole life stage, a new rolling bearing performance evaluation method based on Hilbert-differential local mean decomposition (HDLMD) and Jensen-Renyi divergence (JRD) was proposed. Firstly, the original vibration signal is decomposed by HDLMD and the product function matrix (PF) is extracted. Then, the PF component containing the most fault information is selected based on Laplacian score. Then calculate the probability distribution of the effective PF component after filtering, and obtain the Renyi entropy value of the effective PF component. Finally, the JRD distance between normal signal and signal of different fault degree is calculated, and the degenerate state of rolling bearing is judged. The rolling bearing experimental data from Case Western Reserve University and the life-cycle data from the National Aeronautics and Space Administration show that the proposed method can accurately and effectively evaluate the state of bearing performance degradation.
-
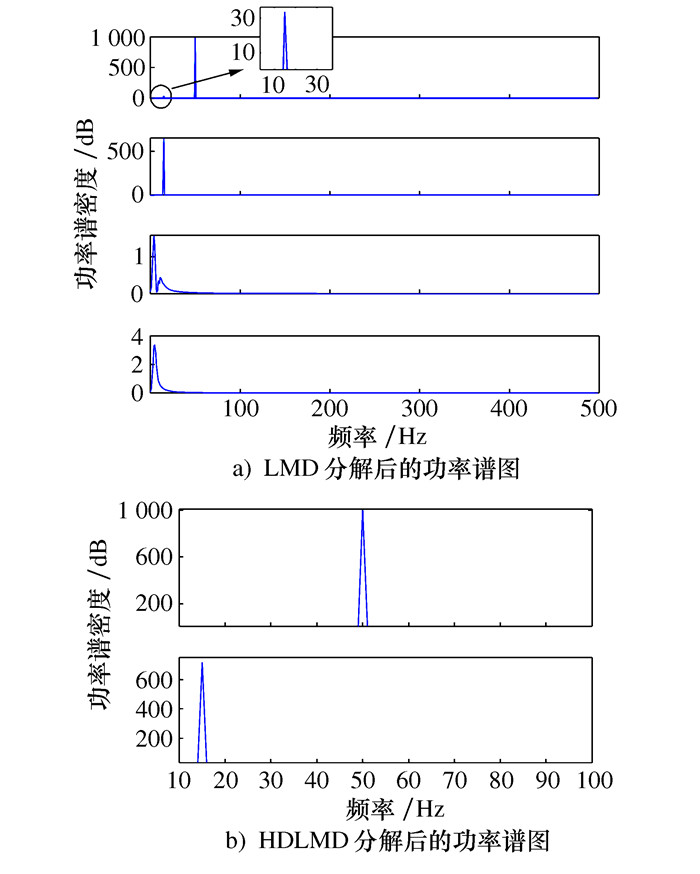
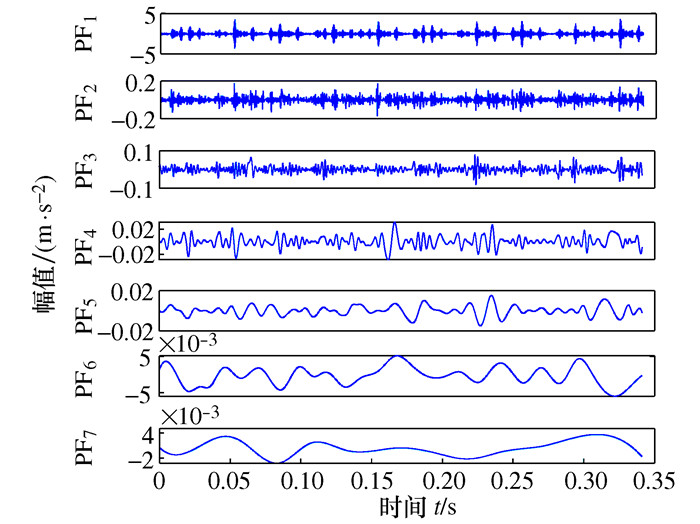
表 1 各PF分量的拉普拉斯分值LS
PF1 PF2 PF3 PF4 PF5 PF6 PF7 0.767 9 0.816 4 0.643 6 0.977 7 1.988 3 4.829 5 6.575 9 表 2 HDLMD和LMD分解的JRD方差对比
方法 方差 HDLMD分解JRD 5.390 7×10-4 LMD分解JRD 9.355 1×10-4 -
[1] 李少鹏. 结合CNN和LSTM的滚动轴承剩余使用寿命预测方法研究[D]. 哈尔滨: 哈尔滨理工大学, 2019LI S P. Research on Remaining Useful life prediction method of a rolling bearing combining CNN and LSTM[D]. Harbin: Harbin University of Science and Technology, 2019 (in Chinese) [2] 郑近德, 潘海洋, 戚晓利, 等. 复合层次模糊熵及其在滚动轴承故障诊断中的应用[J]. 中国机械工程, 2016, 27(15): 2048-2055 doi: 10.3969/j.issn.1004-132X.2016.15.011ZHENG J D, PAN H Y, QI X L, et al. Composite hierarchical fuzzy entropy and its applications to rolling bearing fault diagnosis[J]. China Mechanical Engineering, 2016, 27(15): 2048-2055 (in Chinese) doi: 10.3969/j.issn.1004-132X.2016.15.011 [3] 张小丽, 王保建, 马猛, 等. 滚动轴承寿命预测综述[J]. 机械设计与制造, 2015(10): 221-224 doi: 10.3969/j.issn.1001-3997.2015.10.057ZHANG X L, WANG B J, MA M, et al. A review of life prediction for roller bearing[J]. Machinery Design & Manufacture, 2015(10): 221-224 (in Chinese) doi: 10.3969/j.issn.1001-3997.2015.10.057 [4] 张前图, 房立清, 赵玉龙, 等. 基于LCD信息熵特征和SVM的机械故障诊断[J]. 机械传动, 2015, 39(12): 144-148 https://www.cnki.com.cn/Article/CJFDTOTAL-JXCD201512032.htmZHANG Q T, FANG L Q, ZHAO Y L, et al. Mechanical fault diagnosis based on LCD information entropy feature and SVM[J]. Journal of Mechanical Transmission, 2015, 39(12): 144-148 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXCD201512032.htm [5] 刘美容, 曾黎, 何怡刚, 等. 基于LMD多尺度熵和极限学习机的模拟电路故障诊断[J]. 电子测量与仪器学报, 2017, 31(4): 530-536 https://www.cnki.com.cn/Article/CJFDTOTAL-DZIY201704007.htmLIU M M, ZENG L, HE Y G, et al. Analog circuit fault diagnosis based on LMD multi-scale entropy and extreme learning machine[J]. Journal of Electronic Measurement and Instrumentation, 2017, 31(4): 530-536 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZIY201704007.htm [6] 武哲, 杨绍普, 刘永强. 基于多元经验模态分解的旋转机械早期故障诊断方法[J]. 仪器仪表学报, 2016, 37(2): 241-248 doi: 10.3969/j.issn.0254-3087.2016.02.001WU Z, YANG S P, LIU Y Q. Rotating machinery early fault diagnosis method based on multivariate empirical mode decomposition[J]. Chinese Journal of Scientific Instrument, 2016, 37(2): 241-248 (in Chinese) doi: 10.3969/j.issn.0254-3087.2016.02.001 [7] WANG L, LIU Z W, MIAO Q, et al. Complete ensemble local mean decomposition with adaptive noise and its application to fault diagnosis for rolling bearings[J]. Mechanical Systems and Signal Processing, 2018, 106: 24-39 doi: 10.1016/j.ymssp.2017.12.031 [8] YASIR M N, KOH B H. Data decomposition techniques with multi-scale permutation entropy calculations for bearing fault diagnosis[J]. Sensors, 2018, 18(4): 1278 doi: 10.3390/s18041278 [9] 王志坚, 吴文轩, 马维金, 等. 基于LMD-MS的滚动轴承微弱故障提取方法[J]. 振动、测试与诊断, 2018, 38(5): 1014-1020 https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCS201805023.htmWANG Z J, WU W X, MA W J, et al. Fault signal extraction method of rolling bearing weak fault based on LMD-MS[J]. Journal of Vibration, Measurement & Diagnosis, 2008, 38(5): 1014-1020 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCS201805023.htm [10] 王亚超. 基于局部均值分解的旋转机械故障诊断技术研究[D]. 秦皇岛: 燕山大学, 2015WANG Y C. Research on fault diagnosis technology for rotating machinery based on local mean decomposition[D]. Qinghuangdao: Yanshan University, 2015 (in Chinese) [11] 孟宗, 王亚超, 王晓燕. 基于DLMD样本熵和模糊聚类的滚动轴承故障诊断[J]. 中国机械工程, 2014, 25(19): 2634-2641 doi: 10.3969/j.issn.1004-132X.2014.19.015MENG Z, WANG Y C, WANG X Y. Fault diagnosis of rolling bearings based on DLMD sample entropy and fuzzy clustering[J]. China Mechanical Engineering, 2014, 25(19): 2634-2641 (in Chinese) doi: 10.3969/j.issn.1004-132X.2014.19.015 [12] 孟宗, 季艳. 基于DEMD和对称差分能量算子解调的滚动轴承故障诊断[J]. 中国机械工程, 2015, 26(12): 1658-1664 doi: 10.3969/j.issn.1004-132X.2015.12.018MENG Z, JI Y. Fault diagnosis of rolling bearings based on DEMD and symmetric difference energy operator demodulation[J]. China Mechanical Engineering, 2015, 26(12): 1658-1664 (in Chinese) doi: 10.3969/j.issn.1004-132X.2015.12.018 [13] 崔伟成, 许爱强, 李伟, 等. 基于滑动峭度相关性准则的局部特征尺度分解分量筛选方法[J]. 计算机测量与控制, 2016, 24(10): 233-235, 239 https://www.cnki.com.cn/Article/CJFDTOTAL-JZCK201610068.htmCUI W C, XU A Q, LI W, et al. A method for determining effective components of local characteristic-scale decomposition based on sliding kurtosis correlation coefficients[J]. Computer Measurement & Control, 2016, 24(10): 233-235, 239 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZCK201610068.htm [14] 欧璐, 于德介. 基于拉普拉斯分值和模糊C均值聚类的滚动轴承故障诊断[J]. 中国机械工程, 2014, 25(10): 1352-1357 doi: 10.3969/j.issn.1004-132X.2014.10.015OU L, YU D J. Rolling bearing fault diagnosis based on laplacian score and fuzzy C-means clustering[J]. China Mechanical Engineering, 2014, 25(10): 1352-1357 (in Chinese) doi: 10.3969/j.issn.1004-132X.2014.10.015 [15] YAN X A, JIA M P. A novel optimized SVM classification algorithm with multi-domain feature and its application to fault diagnosis of rolling bearing[J]. Neurocomputing, 2018, 313: 47-64 doi: 10.1016/j.neucom.2018.05.002 [16] 姜海旭, 张科, 王靖宇, 等. 基于形态变分模态分解和JRD的航天器异常状态识别[J]. 西北工业大学学报, 2018, 36(1): 20-27 doi: 10.3969/j.issn.1000-2758.2018.01.004JIANG H X, ZHANG K, WANG J Y, et al. Spacecraft anomaly recognition based on morphological variational mode decomposition and JRD[J]. Journal of Northwestern Polytechnical University, 2018, 36(1): 20-27 (in Chinese) doi: 10.3969/j.issn.1000-2758.2018.01.004 [17] SINGH J, DARPE A K, SINGH S P. Bearing damage assessment using Jensen-Rényi Divergence based on EEMD[J]. Mechanical Systems and Signal Processing, 2017, 87: 307-339 doi: 10.1016/j.ymssp.2016.10.028 [18] SUNOJ S M, LINU M N. Dynamic cumulative residual renyi's entropy[J]. Statistics, 2012, 46(1): 41-56 doi: 10.1080/02331888.2010.494730 [19] 夏均忠, 吕麒鹏, 陈成法, 等. 基于JRD和CUSUM的滚动轴承性能退化状态识别与评估[J]. 振动与冲击, 2019, 38(2): 1-5, 24 https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201902001.htmXIA J Z, LU Q P, CHEN C F, et al. Performance degradation status identification and assessment of rolling element bearing based on the JRD and CUSUM[J]. Journal of Vibration and Shock, 2019, 38(2): 1-5, 24 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201902001.htm [20] HE X F, CAI D, NIYOGI P. Laplacian score for feature selection[C]//Proceedings of the 18th International Conference on Neural Information Processing Systems. British: NIPS, 2005: 507-514 [21] 程军圣, 郑近德, 杨宇, 等. 基于部分集成局部特征尺度分解与拉普拉斯分值的滚动轴承故障诊断模型[J]. 振动工程学报, 2014, 27(6): 942-950 doi: 10.3969/j.issn.1004-4523.2014.06.020CHENG J S, ZHENG J D, YANG Y, et al. Fault diagnosis model for rolling bearing based on partly ensemble local characteristic-scale decomposition and Laplacian score[J]. Journal of Vibration Engineering, 2014, 27(6): 942-950 (in Chinese) doi: 10.3969/j.issn.1004-4523.2014.06.020 [22] 蔡源春. 汽车变速器轴承故障诊断研究[D]. 长沙: 湖南大学, 2007CAI Y C. Research of diagnosis on the fault of the rolling element bearing in transmission[D]. Changsha: Hunan University, 2007 (in Chinese) [23] QIU H, LEE J, LIN J, et al. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics[J]. Journal of Sound and Vibration, 2006, 289(4-5): 1066-1090 doi: 10.1016/j.jsv.2005.03.007 -







 下载:
下载: