Planning Warehouse AGV Path with Parallel-ranking Ant Colony Optimization Algorithm
-
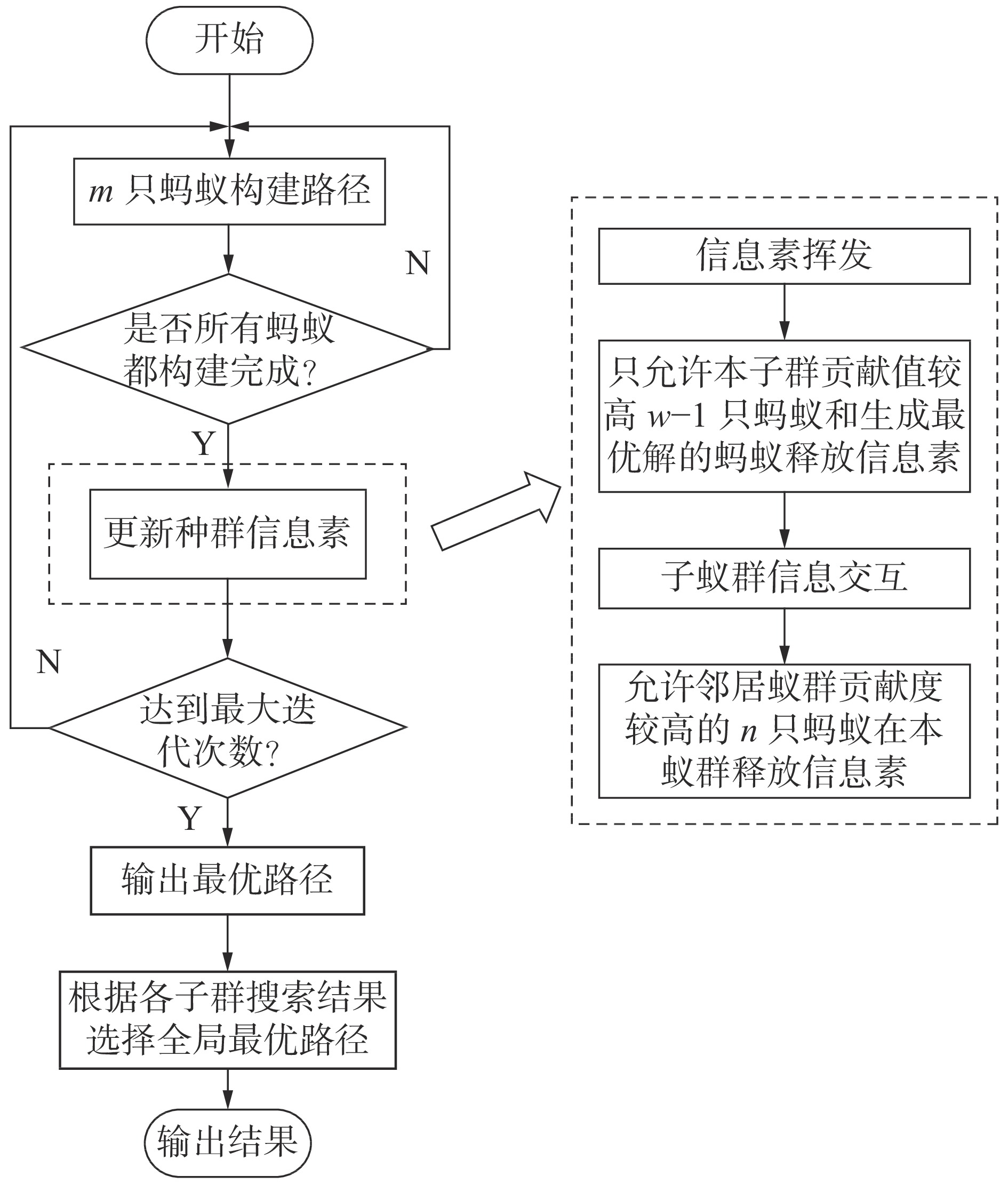
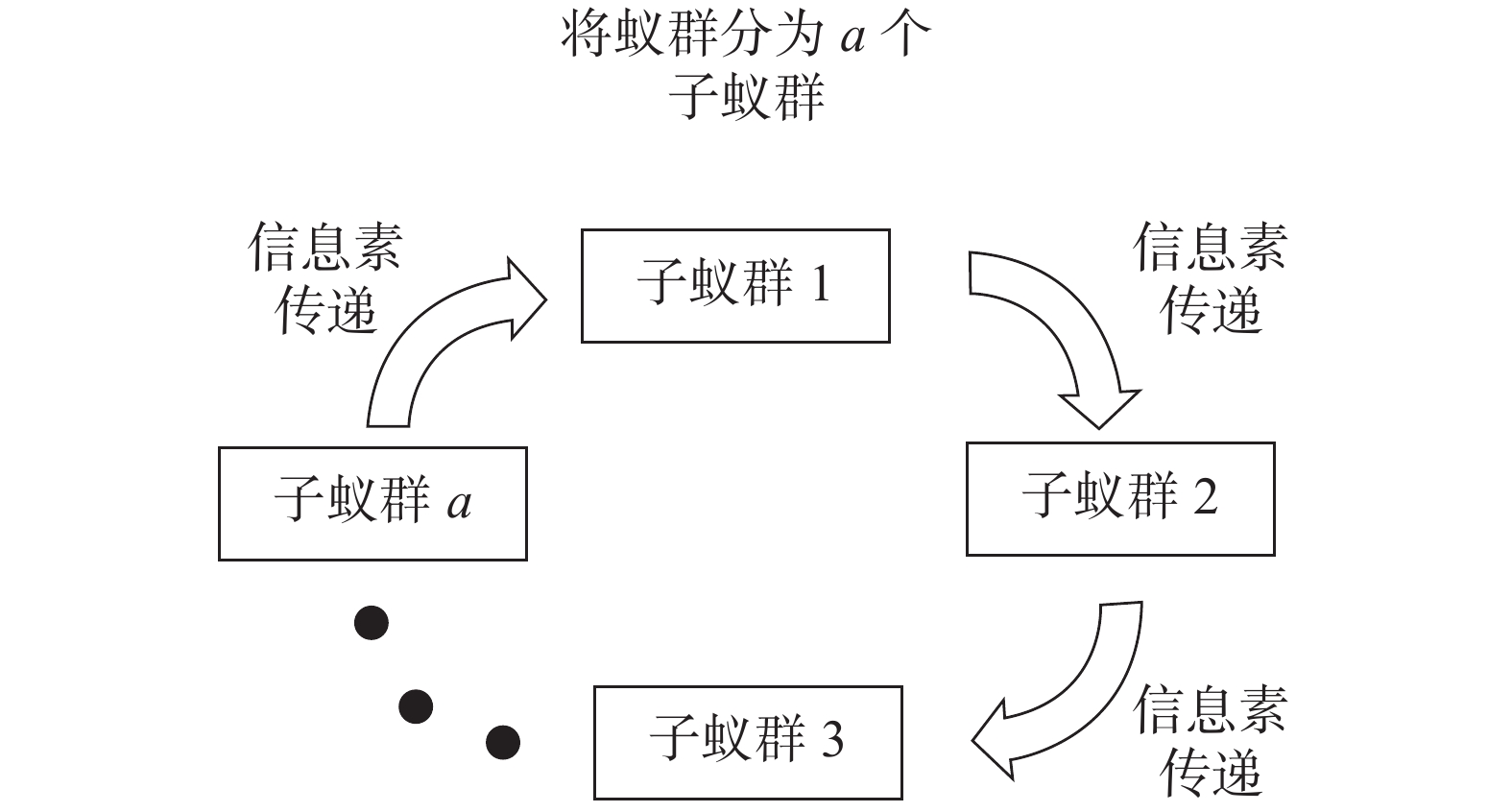
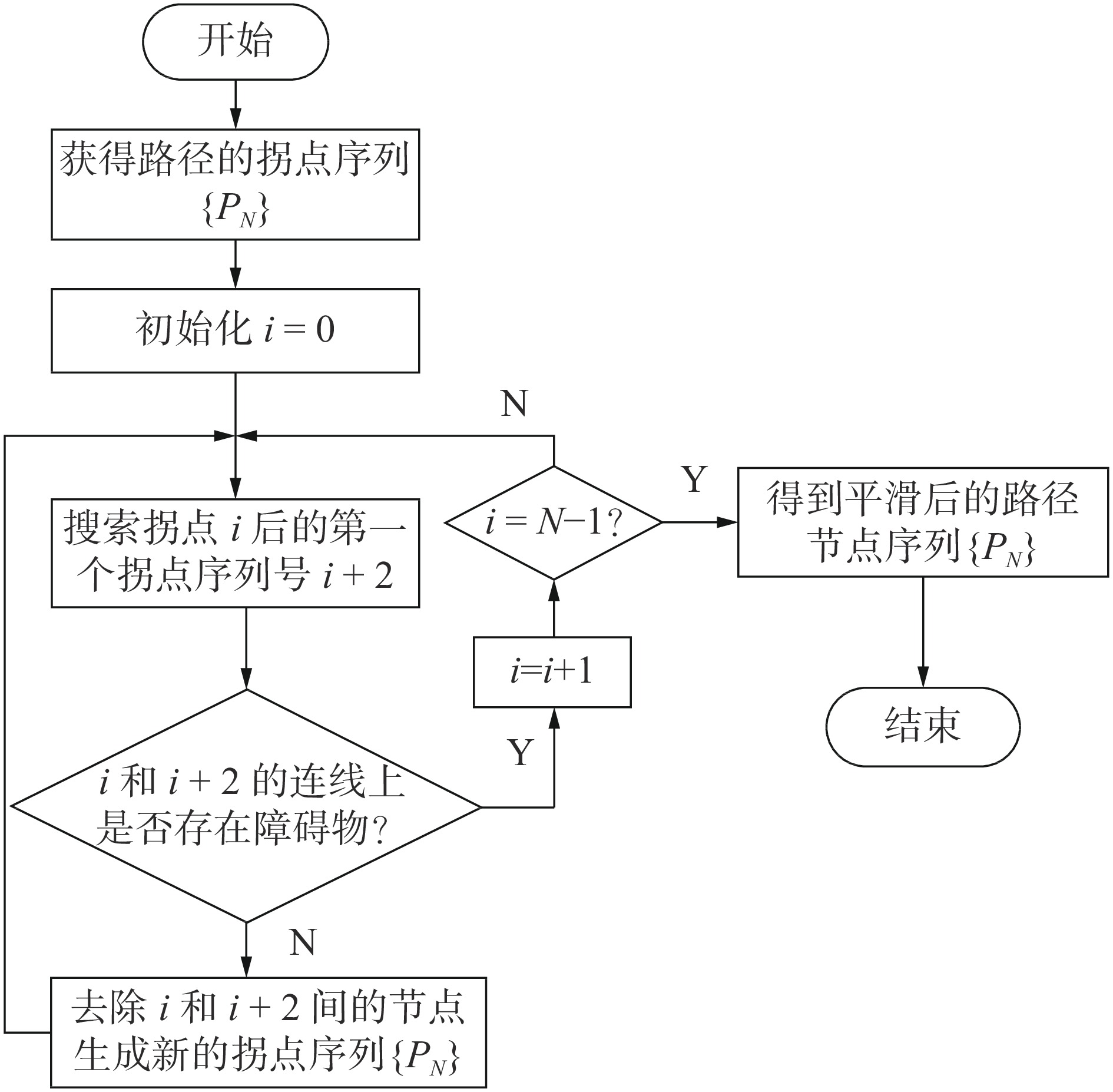
摘要: 针对智能仓库中的AGV路径规划问题,提出了一种基于并行排序蚁群算法的路径规划方法,该方法通过多个子蚁群之间较优蚂蚁释放的信息素交互,提高蚁群整体的搜索能力。建立以路径最短和AGV转弯次数最少为优化目标的多目标函数模型,用并行排序蚁群算法求解,再对生成的初始路径通过减少中间节点的方式进行平滑处理。在MATLAB上进行多次仿真,对比实验结果表明,该算法在进行仓库AGV路径规划时收敛速度更快,稳定性更好,且平滑处理后的路径更优。Abstract: To plan thepath of an automatically guided vehicle (AGV) in an intelligent warehouse, a path planning method based on theparallel-rankting ant colony optimizationalgorithm is proposed. The method improves its overall search ability through the pheromone interaction released by superior ants among multiple ant sub-colonies. A multi-objective optimization function model with the shortest path and the least number of turns of the AGV as optimization objectives is established and is solved with theparallel-rankingant colony optimizationalgorithm.The initial pathgenerated with the optimization algorithmis smoothed by reducing intermediate nodes. The MATLABcomputer simulation results show that the method has better stability and convergence speed and that the smoothing is effective.
-
表 1 求解TSP问题时4种算法50次仿真结果
名称 ACO RACO IAC[17] P-RACO 路径
长度Max 3363.04 3189.25 3177.26 3152.51 Min 3101.32 3068.44 3076.98 3058.93 Avg 3161.35 3189.25 3116.51 3102.16 Sd 66.59 28.56 28.11 22.01 迭代
次数Max 97 42 28 19 Min 10 7 5 3 Avg 17.22 10.30 9.42 6.02 Sd 16.25 6.60 5.43 3.39 表 2 30 × 30环境中4种算法50次仿真结果
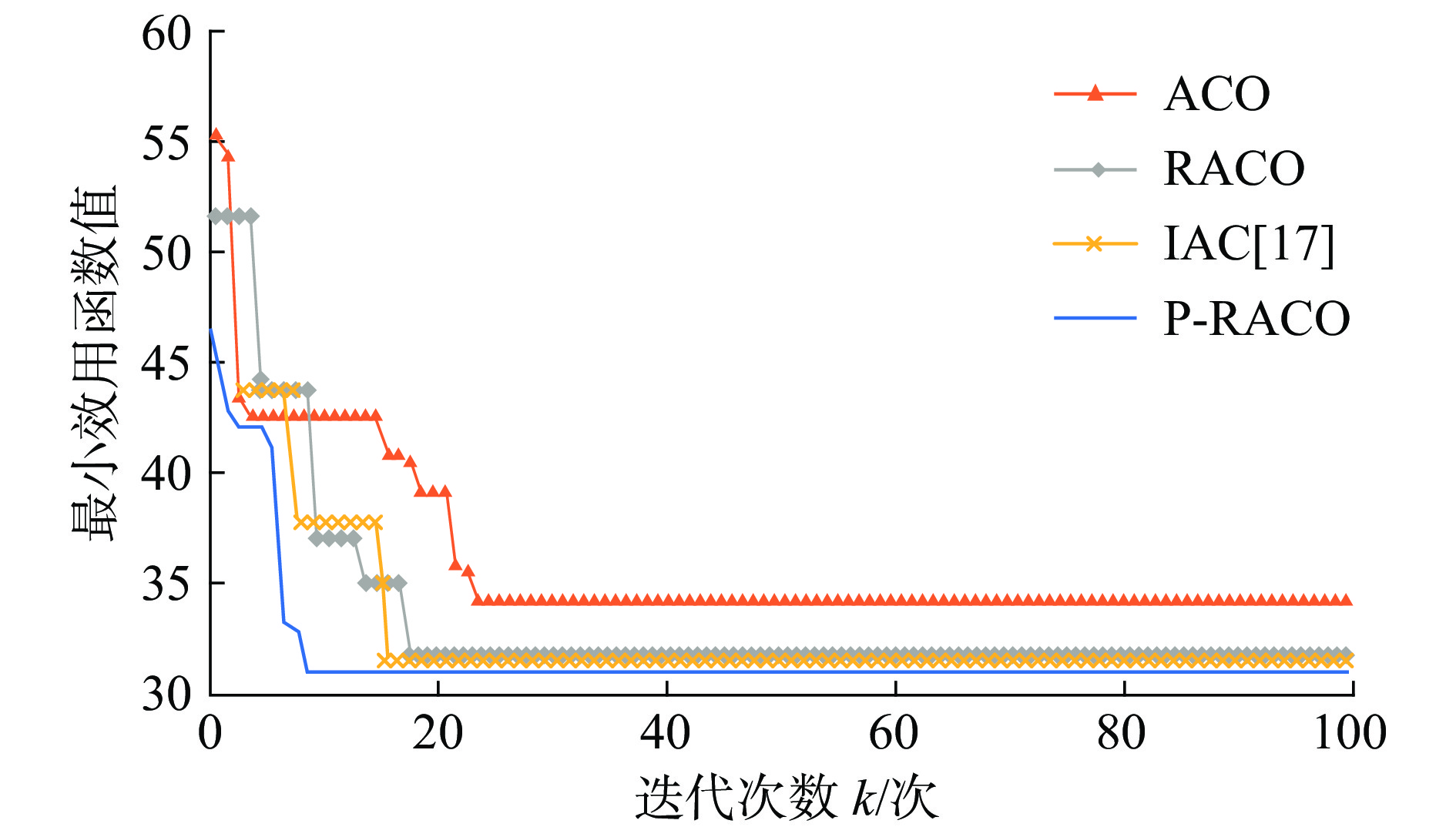
名称 ACO RACO IAC[17] P-RACO 效用函
数值Max 35.278 34.456 34.987 34.067 Min 30.726 30.712 30.352 29.872 Avg 32.647 32.107 31.887 30.933 Sd 1.458 1.112 1.192 0.823 迭代
次数Max 32 26 26 10 Min 19 16 14 8 Avg 24.58 18.44 16.72 8.72 Sd 3.112 2.475 2.807 0.491 表 3 35 × 35环境中4种算法50次仿真结果
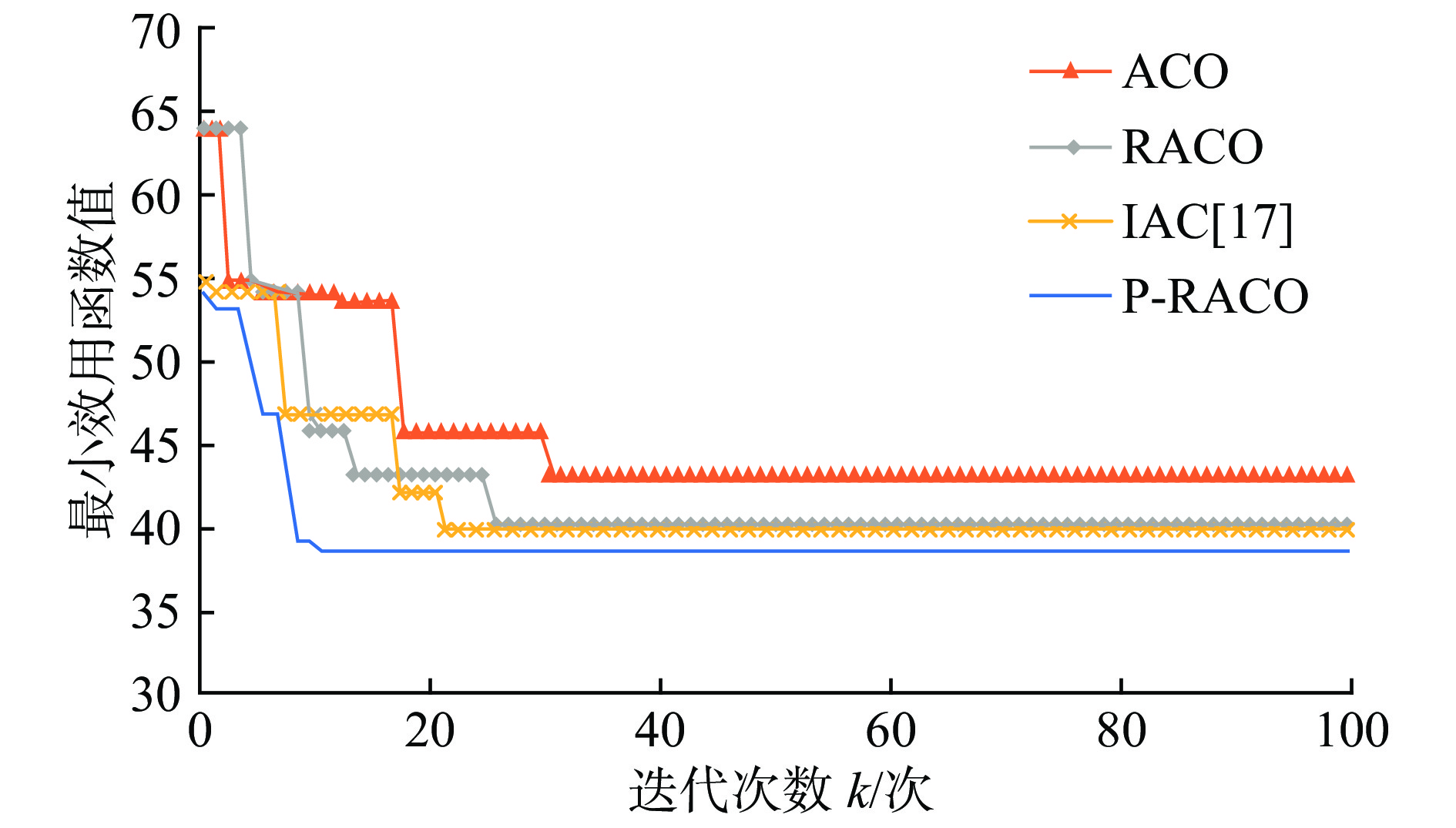
名称 ACO RACO IAC[17] P-RACO 效用函
数值Max 48.797 44.776 48.747 42.118 Min 40.477 40.001 38.507 38.282 Avg 44.420 43.346 42.336 40.049 Sd 3.147 2.208 1.965 0.968 迭代
次数Max 37 33 29 12 Min 27 20 19 9 Avg 31.86 24.60 23.04 10.08 Sd 2.550 1.989 1.199 0.483 表 4 不同复杂度地图30次仿真结果对比
名称 ACO RACO IAC[17] P-RACO 20 × 20 效用
函数Avg 27.525 26.902 26.633 26.630 Sd 0.878 0.345 0.432 0.159 迭代
次数Avg 16.42 10.20 10.33 5.63 Sd 3.657 1.876 2.103 0.796 40 × 40 效用
函数Avg 68.763 63.234 59.989 57.97 Sd 6.072 4.234 3.546 3.354 迭代
次数Avg 36.42 24.34 19.46 11.91 Sd 3.094 1.937 1.675 0.907 50 × 50 效用
函数Avg 100.044 92.987 89.879 81.369 Sd 6.157 5.629 4.982 3.771 迭代
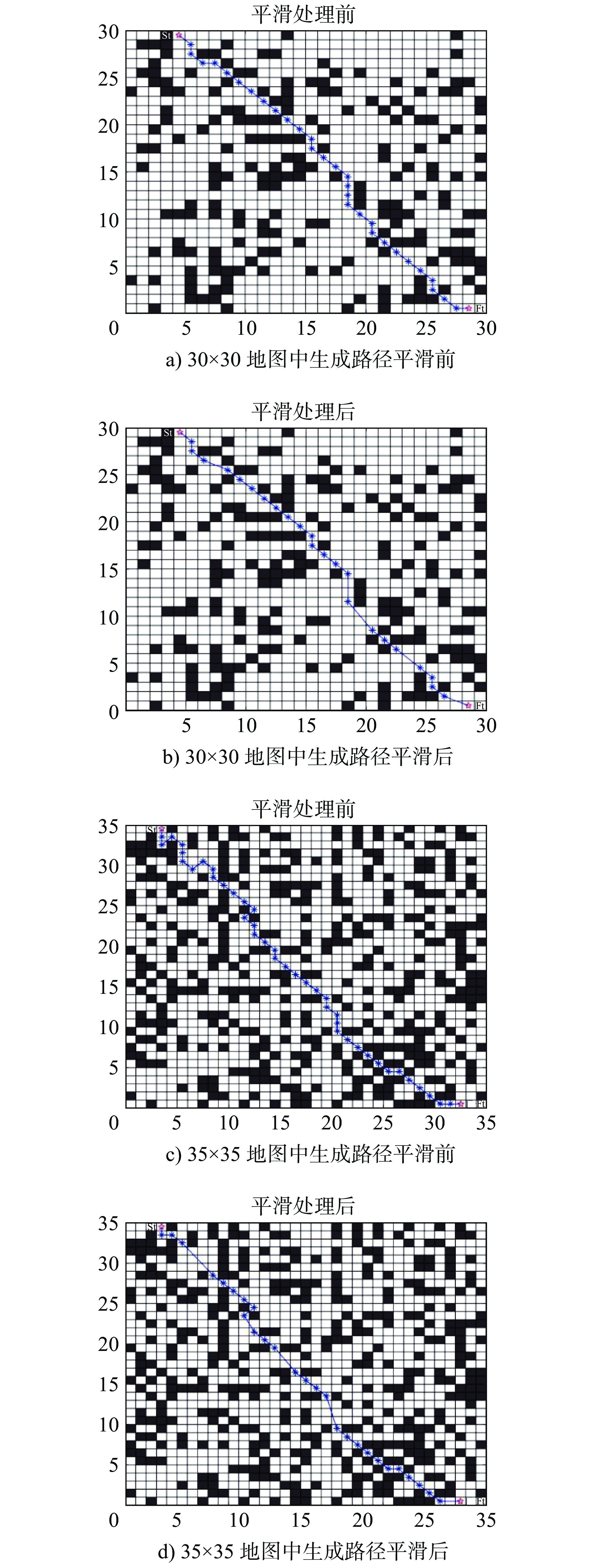
次数Avg 42.88 28.98 39.67 13.65 Sd 3.066 2.376 2.256 1.424 表 5 路径平滑前后数据对比
名称 30 × 30 35 × 35 平滑前路径长度 40.113 52.598 平滑后路径长度 38.291 48.249 路径长度减少量 4.5% 8.3% 平滑前转弯次数 13 21 平滑后转弯次数 12 14 转弯次数减少量 7.6% 33.3% -
[1] 梁建刚. AGV系统路径规划与调度算法研究[D]. 北京: 北京邮电大学, 2018.LIANG J G. Research on path planning and scheduling algorithm of AGV system[D]. Beijing: Beijing University of Posts and Telecommunications, 2018 (in Chinese). [2] KANG N K, SON H J, LEE S H. Modified A-star algorithm for modular plant land transportation[J]. Journal of Mechanical Science and Technology, 2018, 32(12): 5563-5571 doi: 10.1007/s12206-018-1102-z [3] 乐阳, 龚健雅. Dijkstra最短路径算法的一种高效率实现[J]. 武汉测绘科技大学学报, 1999, 24(3): 209-212 doi: 10.3969/j.issn.1671-8860.1999.03.005YUE Y, GONG J Y. An efficient implementation of shortest path algorithm based on Dijkstra algorithm[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1999, 24(3): 209-212 (in Chinese) doi: 10.3969/j.issn.1671-8860.1999.03.005 [4] 王树西, 李安渝. Dijkstra算法中的多邻接点与多条最短路径问题[J]. 计算机科学, 2014, 41(6): 217-224 doi: 10.11896/j.issn.1002-137X.2014.06.043WANG S X, LI A Y. Multi-adjacent-vertexes and multi-shortest-paths problem of Dijkstra algorithm[J]. Computer Science, 2014, 41(6): 217-224 (in Chinese) doi: 10.11896/j.issn.1002-137X.2014.06.043 [5] CHEN X, KONG Y Y, FANG X, et al. A fast two-stage ACO algorithm for robotic path planning[J]. Neural Computing and Applications, 2013, 22(2): 313-319 doi: 10.1007/s00521-011-0682-7 [6] YANG H, QI J, MIAO Y C, et al. A new robot navigation algorithm based on a double-layer ant algorithm and trajectory optimization[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8557-8566 doi: 10.1109/TIE.2018.2886798 [7] 何庆, 吴意乐, 徐同伟. 改进遗传模拟退火算法在TSP优化中的应用[J]. 控制与决策, 2018, 33(2): 219-225HE Q, WU Y L, XU T W. Application of improved genetic simulated annealing algorithm in TSP optimization[J]. Control and Decision, 2018, 33(2): 219-225 (in Chinese) [8] 贾全, 张小超, 苑严伟, 等. 拖拉机自动驾驶系统上线轨迹规划方法[J]. 农业机械学报, 2018, 49(4): 36-44 doi: 10.6041/j.issn.1000-1298.2018.04.004JIA Q, ZHANG X C, YUAN Y W, et al. Guided trajectory planning method for tractor autopilot system[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(4): 36-44 (in Chinese) doi: 10.6041/j.issn.1000-1298.2018.04.004 [9] COUCEIRO M S, MACHADO J A T, ROCHA R P, et al. A fuzzified systematic adjustment of the robotic Darwinian PSO[J]. Robotics and Autonomous Systems, 2012, 60(12): 1625-1639 doi: 10.1016/j.robot.2012.09.021 [10] 孔令文, 李鹏永, 杜巧玲. 基于模糊神经网络的六足机器人自主导航闭环控制系统设计[J]. 机器人, 2018, 40(1): 16-23KONG L W, LI P Y, DU Q L. The closed-loop control system design of hexapod robot autonomous navigation based on fuzzy neural network[J]. Robot, 2018, 40(1): 16-23 (in Chinese) [11] DORIGO M, GAMBARDELLA L M. Ant colony system: a cooperative learning approach to the traveling salesman problem[J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 53-66 doi: 10.1109/4235.585892 [12] 金弟, 杨博, 刘杰, 等. 复杂网络簇结构探测——基于随机游走的蚁群算法[J]. 软件学报, 2012, 23(3): 451-464 doi: 10.3724/SP.J.1001.2012.03996JIN D, YANG B, LIU J, et al. Ant colony optimization based on random walk for community detection in complex networks[J]. Journal of Software, 2012, 23(3): 451-464 (in Chinese) doi: 10.3724/SP.J.1001.2012.03996 [13] STÜTZLE T, HOOS H H. MAX-MIN ant system[J]. Future Generation Computer Systems, 2000, 16(8): 889-914 doi: 10.1016/S0167-739X(00)00043-1 [14] 刘利强, 袁赣南, 戴运桃. 多蚁群伪并行优化算法[J]. 计算机工程, 2007, 33(23): 199-201 doi: 10.3969/j.issn.1000-3428.2007.23.069LIU L Q, YUAN G N, DAI Y T. Multi-ant colony virtual parallel optimization algorithm[J]. Computer Engineering, 2007, 33(23): 199-201 (in Chinese) doi: 10.3969/j.issn.1000-3428.2007.23.069 [15] LIU J H, YANG J G, LIU H P, et al. An improved ant colony algorithm for robot path planning[J]. Soft Computing, 2017, 21(19): 5829-5839 doi: 10.1007/s00500-016-2161-7 [16] 王晓燕, 杨乐, 张宇, 等. 基于改进势场蚁群算法的机器人路径规划[J]. 控制与决策, 2018, 33(10): 1775-1781WANG X Y, YANG L, ZHANG Y, et al. Robot path planning based on improved ant colony algorithm with potential field heuristic[J]. Control and Decision, 2018, 33(10): 1775-1781 (in Chinese) [17] ZHANG Y, WANG F L, FU F K, et al. Multi-AGV Path planning for indoor factory by using prioritized planning and improved ant algorithm[J]. Journal of Engineering and Technological Sciences, 2018, 50(4): 534-547 doi: 10.5614/j.eng.technol.sci.2018.50.4.6 [18] 乔辰, 张国立. 几何加权法求解多目标规划问题[J]. 华北电力大学学报, 2011, 38(6): 107-110QIAO C, ZHANG G L. Geometric weighting method for solving multi-objective programming problems[J]. Journal of North China Electric Power University, 2011, 38(6): 107-110 (in Chinese) [19] WANG D S, YU H F. Path planning of mobile robot in dynamic environments[C]//2011 2nd International Conference on Intelligent Control and Information Processing. Harbin: IEEE, 2011. [20] 孙波, 姜平, 周根荣, 等. 改进遗传算法在移动机器人路径规划中的应用[J/OL]. 计算机工程与应用, 2019(2019-06-03). http://kns.cnki.Net/kcms/detail/11.2127.tp.20190530.1022.018.html.SUN B, JIANG P, ZHOU G R, et al. Application of improved genetic algorithm in path planning of mobile robots[J/OL]. Computer Engineering and Applications, 2019(2019-06-03). http://kns.cnki.Net/kcms/detail/11.2127.tp.20190530.1022.018.html (in Chinese). [21] 屈鸿, 黄利伟, 柯星. 动态环境下基于改进蚁群算法的机器人路径规划研究[J]. 电子科技大学学报, 2015, 44(2): 260-265 doi: 10.3969/j.issn.1001-0548.2015.02.017QU H, HUANG L W, KE X. Research of improved ant colony based robot path planning under dynamic environment[J]. Journal of University of Electronic Science and Technology of China, 2015, 44(2): 260-265 (in Chinese) doi: 10.3969/j.issn.1001-0548.2015.02.017 [22] 黄辰, 费继友, 刘洋, 等. 基于动态反馈A*蚁群算法的平滑路径规划方法[J]. 农业机械学报, 2017, 48(4): 34-40, 102 doi: 10.6041/j.issn.1000-1298.2017.04.004HUANG C, FEI J Y, LIU Y, et al. Smooth path planning method based on dynamic feedback A* ant colony algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(4): 34-40, 102 (in Chinese) doi: 10.6041/j.issn.1000-1298.2017.04.004 -








 下载:
下载: