Vibration Analysis of Laminated Composite Beams with Elastic Boundary Conditions
-
摘要: 在一阶剪切变形理论和哈密顿原理的基础上,利用Haar小波离散方法,提出了一种简单、有效的评估一般弹性边界条件下复合材料层合梁振动特性的分析模型。结构位移变量及其相关导数的基函数分别采用Haar小波及其积分表示。在此基础上,利用边界条件求出积分过程中的常数,进而将层合梁的运动方程和边界条件进一步转化为一组线性代数方程。通过求解该线性代数方程,可得到复合材料层合梁的自由振动特性。通过数值算例对比验证了本文模型的正确性。此外,给出了复合材料层合梁的一些新的计算结果,可作为基准解为后续数值方法或解析法提供对比数据。Abstract: A simple and efficient method is proposed to evaluate the vibration behavior of the laminated composite beams under elastic boundary conditions with Haar wavelet discretization method, in terms of the first order shear deformation theory and the Hamilton principle. The basis functions for the displacement variables and their derivatives are expressed in terms of Haar wavelet and their integral, respectively. On the basis, the boundary conditions are used to obtain the constants in the integration process, and then the equations of motion and the boundary conditions of the laminated beams are further converted into a group of linear algebraic equations. The natural frequencies of laminated composite beams are obtained by solving the algebraic equations. The correctness and efficiency of the present method is verified by a series of numerical examples. Some new results for the laminated composite beams are presented, which may serve as benchmark solutions.
-
表 1 不同边界条件下对应的弹簧刚度值
弹簧
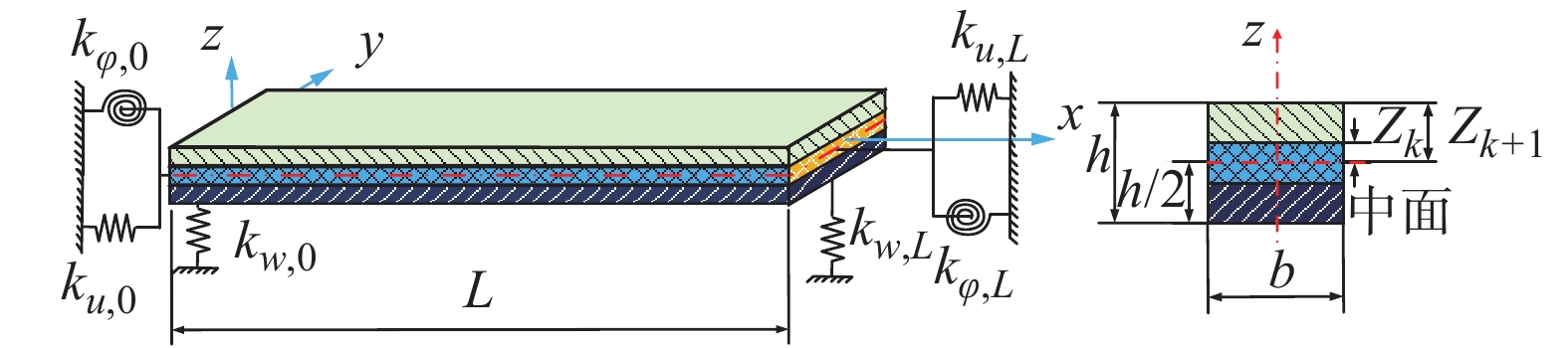
类型经典边界条件 弹性边界条件 F S C E1 E2 E3 ${k_u}_{,0},\;{k_u}_{,L}$ 0 1014 1014 108 1014 108 ${k_{w,}}_0,\;{k_{w,}}_L$ 0 1014 1014 108 1014 108 ${k_{\varphi ,0}},\;{k_{\varphi ,L}}$ 0 0 1014 1014 108 108 表 2 不同边界条件下复合材料层合梁固有频率对比
边界
条件模态
阶次本文
方法文献
[12]文献
[13]文献
[14]1 639.08 638.50 637.20 637.90 2 1 656.3 1 657.3 1 653.2 1 647.8 C-C 3 3 026.6 3 034.0 3 025.0 3 000.0 4 4 640.2 4 661.2 4 644.8 3 911.0 5 4 950.6 4 784.6 4 960.8 4 587.3 1 105.49 105.30 105.10 105.30 2 638.40 637.60 636.40 635.00 C-F 3 1 698.9 1 698.0 1 694.2 1 678.9 4 2 475.5 2 392.3 2 480.6 1 970.6 5 3 119.7 3 121.0 3 113.2 2 546.2 1 660.42 659.30 659.20 655.00 2 1 741.8 1 738.6 1 735.2 1 719.2 F-F 3 3 219.5 3 213.4 3 207.2 3 128.8 4 4 951.2 4 784.8 4 948.0 3 966.8 5 4 969.8 4 961.0 4 961.6 4 836.5 1 295.33 294.80 294.90 353.70 2 1 134.5 1 132.4 1 130.2 1 114.3 S-S 3 2 418.9 2 414.4 2 490.6 2 434.2 4 4 021.2 4 012.3 4 001.1 3 450.3 5 4 949.3 4 784.2 4 952.9 4 264.5 1 451.09 450.50 449.80 467.30 2 1 390.9 1 389.9 1 387.0 1 391.3 S-C 3 2 723.9 2 724.1 2 717.5 2 685.5 4 4 336.0 4 340.4 4 327.8 3 757.0 5 4 949.6 4 784.3 4 956.1 4 366.8 表 3 不同边界条件下复合材料层合梁固有频率对比
模态阶次 边界条件 C-C C-F S-C S-S 本文方法 文献[12] 文献[14] 本文方法 文献[12] 本文方法 文献[12] 本文方法 文献[12] 1 1 054.598 1 054.503 1 054.4 191.85 191.80 785.07 784.90 559.04 558.90 2 2 509.615 2 509.363 2 509.2 1 088.6 1 088.5 2 224.2 2 223.9 1 908.0 1 907.7 3 4 282.239 4 281.739 4 281.5 2 694.2 1 132.7 4 039.2 4 038.6 3 787.8 3 787.2 4 6 216.956 6 216.093 6 215.8 4 598.9 2 265.4 6 032.6 6 301.5 5 826.0 5 824.8 5 8 241.754 8 240.392 8 239.9 4 905.2 2 693.8 8 106.6 8 104.8 7 982.3 7 980.5 -
[1] 缪馥星, 孙国钧. 非对称层合梁瞬态响应回传射线矩阵法解[J]. 振动与冲击, 2015, 34(20): 1-5Miao F X, Sun G J. Transient dynamic response analysis of asymmetric laminated composite beam by using the reverberation-ray matrix method[J]. Journal of Vibration and Shock, 2015, 34(20): 1-5 (in Chinese) [2] 李乐, 何录武, 闵国林. 复合材料层合梁的横向剪应力分析[J]. 兰州大学学报, 2001, 37(5): 15-22Li L, He L W, Min G L. Analysis of transverse shear stresses for composite laminated beams[J]. Journal of Lanzhou University , 2001, 37(5): 15-22 (in Chinese) [3] 邹爱丽, 任晓辉, 秦政琪. 复合材料层合梁和夹层梁屈曲问题数值分析[J]. 工程力学, 2011, 28(4): 134-137Zou A L, Ren X H, Qin Z Q. Buckling analysis of laminated composite and sandwich beams[J]. Engineering Mechanics, 2011, 28(4): 134-137 (in Chinese) [4] 邱志平, 邱薇, 王晓军. 复合材料层合梁自由振动的区间分析[J]. 北京航空航天大学学报, 2006, 32(7): 838-842 doi: 10.3969/j.issn.1001-5965.2006.07.020Qiu Z P, Qiu W, Wang X J. Interval analysis for free vibration of composite laminated beams[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(7): 838-842 (in Chinese) doi: 10.3969/j.issn.1001-5965.2006.07.020 [5] 惠维维, 韩宾, 张钱城, 等. 基于一种简化剪切变形理论的层合梁自由振动分析[J]. 应用力学学报, 2017, 34(6): 1067-1071Hui W W, Han B, Zhang Q C, et al. Free vibration analysis of laminated composite beams based on a simplified shear deformation theory[J]. Chinese Journal of Applied Mechanics, 2017, 34(6): 1067-1071 (in Chinese) [6] 刘湘龙. 具脱层复合材料梁动力特性研究[D]. 长沙: 长沙理工大学, 2015Liu X L. Dynamic analysis of composite beam structure with delamination[D]. Changsha: Changsha University of Science & Technology, 2015 (in Chinese) [7] 杜杰, 吴振. 热环境下复合材料层合梁自由振动分析[J]. 沈阳航空航天大学学报, 2017, 34(6): 55-59, 77 doi: 10.3969/j.issn.2095-1248.2017.06.009Du J, Wu Z. Free vibration analysis of laminated composite beam under thermal environment[J]. Journal of Shenyang Aerospace University, 2017, 34(6): 55-59, 77 (in Chinese) doi: 10.3969/j.issn.2095-1248.2017.06.009 [8] 蒋宝坤. 湿热环境下旋转复合材料层合梁振动特性研究[D]. 成都: 西南交通大学, 2014Jiang B K. The vibration characteristic analysis of a rotating laminated composite beam under hygrothermal environment[D]. Chengdu: Southwest Jiaotong University, 2014 (in Chinese) [9] Chen W J, Li L, Xu M. A modified couple stress model for bending analysis of composite laminated beams with first order shear deformation[J]. Composite Structures, 2011, 93(11): 2723-2732 doi: 10.1016/j.compstruct.2011.05.032 [10] Oñate E, Eijo A, Oller S. Simple and accurate two-noded beam element for composite laminated beams using a refined zigzag theory[J]. Computer Methods in Applied Mechanics and Engineering, 2012, 213-216: 362-382 doi: 10.1016/j.cma.2011.11.023 [11] Mohammadabadi M, Daneshmehr A R, Homayounfard M. Size-dependent thermal buckling analysis of micro composite laminated beams using modified couple stress theory[J]. International Journal of Engineering Science, 2015, 92: 47-62 doi: 10.1016/j.ijengsci.2015.03.005 [12] Li J, Hua H X. Dynamic stiffness analysis of laminated composite beams using trigonometric shear deformation theory[J]. Composite Structures, 2009, 89(3): 433-442 doi: 10.1016/j.compstruct.2008.09.002 [13] Li J, Hua H X, Shen R Y. Dynamic finite element method for generally laminated composite beams[J]. International Journal of Mechanical Sciences, 2008, 50(3): 466-480 doi: 10.1016/j.ijmecsci.2007.09.014 [14] Qu Y G, Long X H, Li H G, et al. A variational formulation for dynamic analysis of composite laminated beams based on a general higher-order shear deformation theory[J]. Composite Structures, 2013, 102: 175-192 doi: 10.1016/j.compstruct.2013.02.032 [15] 谢祥. Haar小波法及其在结构振动分析中的应用[D]. 哈尔滨: 哈尔滨工程大学, 2014Xie X. Haar wavelet method and research on its application in structural vibration analysis[D]. Harbin: Harbin Engineering University, 2014 (in Chinese) -







 下载:
下载: