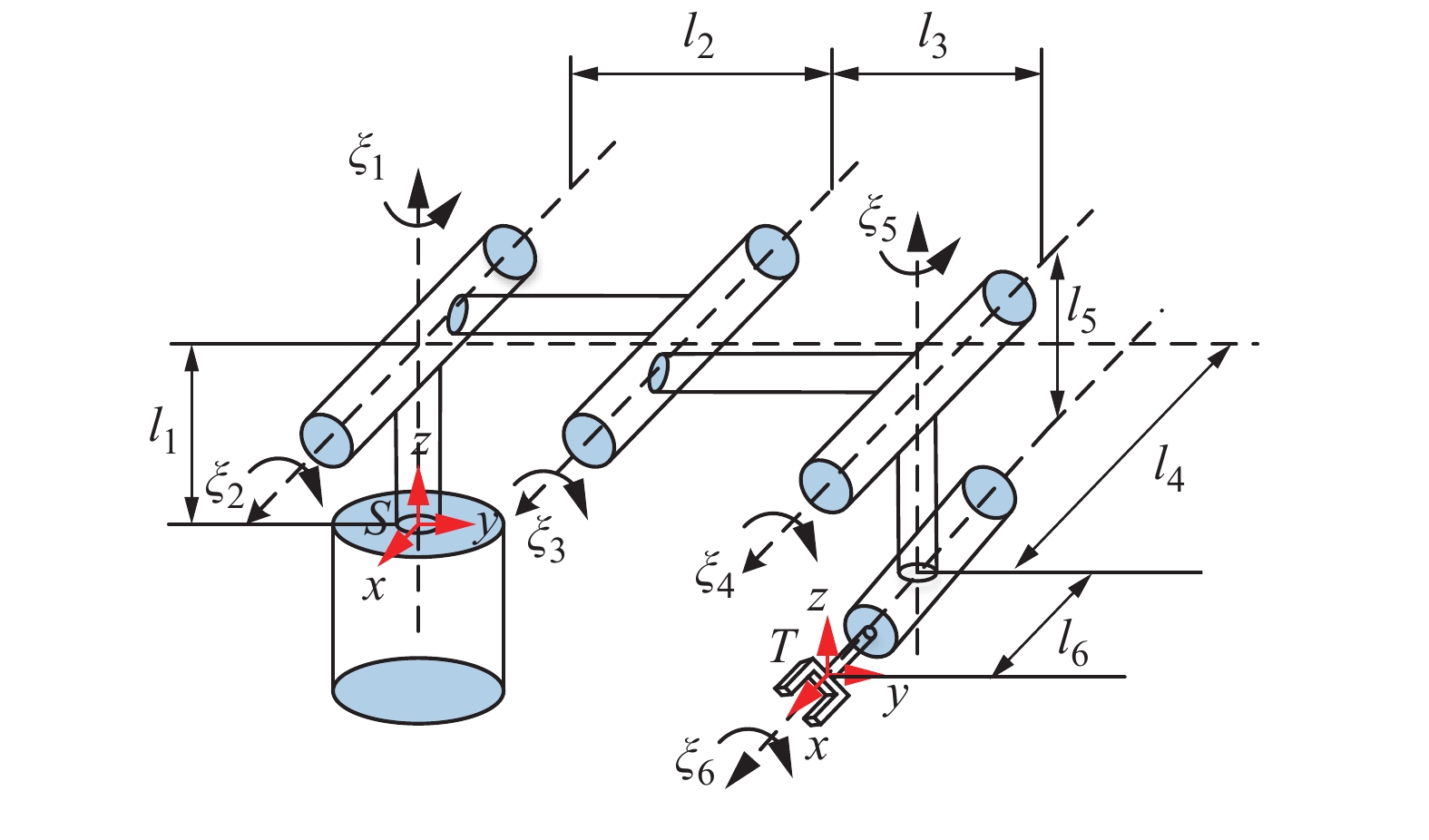
Analyzing Workspace of Sewing Robot
-
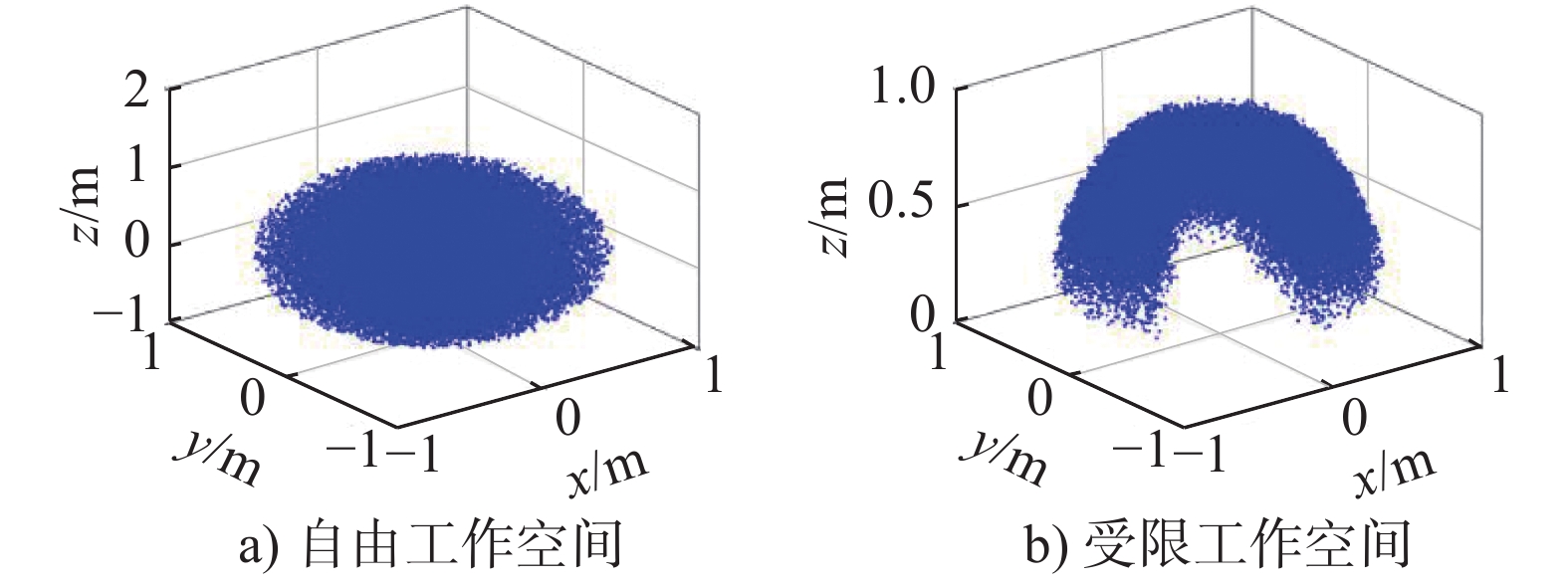
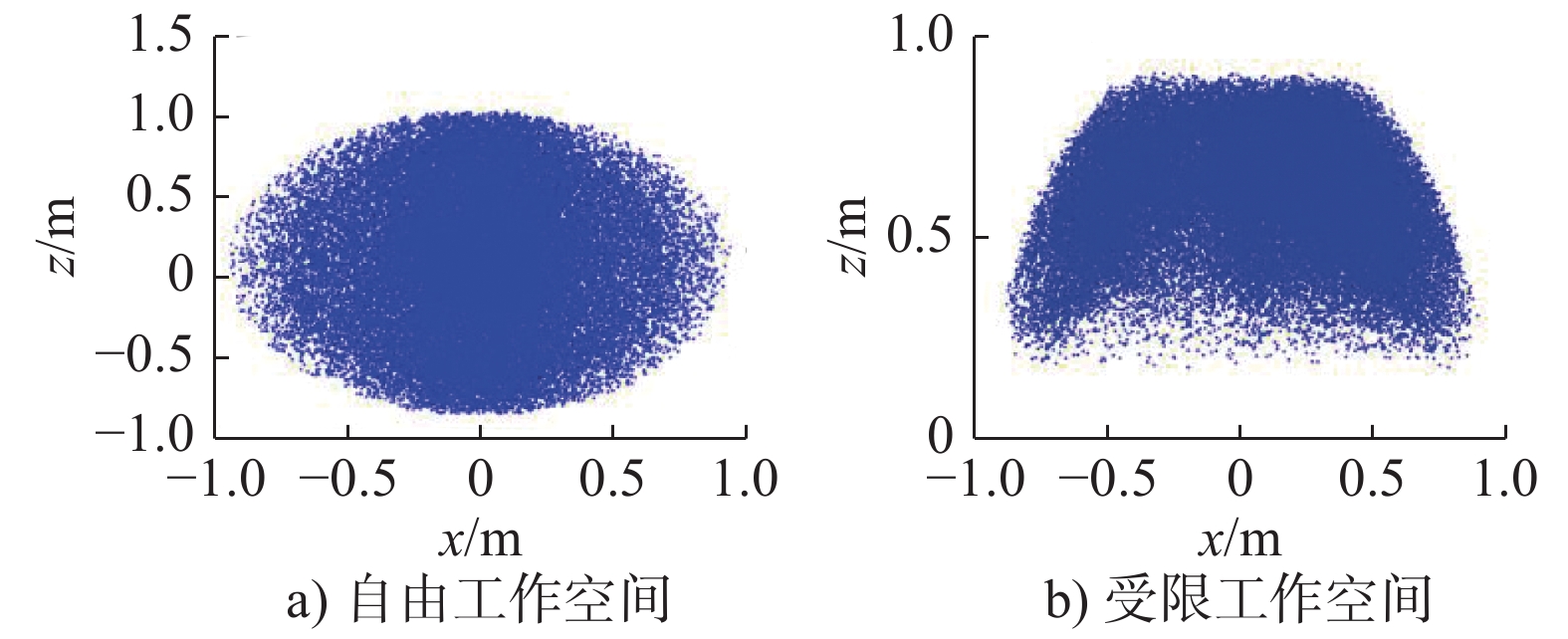
摘要: 为确定符合缝纫机结构条件的缝纫机器人工作空间,提高机器人缝纫作业前的规划效率,应用旋量法建立运动学模型,并使用Adams软件验证了所建运动学模型的正确性。采用蒙特卡洛法结合控制变量法分析具有区域限制性的工作空间,确定出机器人各关节在实际工作环境中最佳的转角范围。利用MATLAB仿真得到机器人自由与受限情况下的工作空间云图,对比结果表明所确定的关节转角范围满足机器人实际的工作空间要求。Abstract: In order to determine the sewing robot′s workspace so as to meet its structural conditions and to improve the planning efficiency before its operation,its kinematics model is established with the screw theory.The correctness of the kinematic model is verified with the Adams software. The Monte Carlo method together with the control variable method is used to analyze the workspace that has regional restrictions and to determine the optimal range of rotation angles for each joint of the sewing robot in its actual working environment. The free and limited conditions of the cloud map of its workspace are simulated with the MATLAB. The simulation results show that the joint rotation angle range determined in this paper satisfies the actual workspace requirements of the sewing robot and provides a theoretical basis for the follow-up research of it.
-
Key words:
- sewing robot /
- screw theory /
- kinematics /
- workspace
-
表 1 机器人末端位移理论值与实际值对比
m 位移 1 2 3 ${p_x}$ 0.6273 0.4824 0.4304 ${p_y}$ 0.1887 0.2272 0.4107 ${p_{\textit{z}}}$ 0.0678 0.2901 0.3382 ${p_1}$ 0.6274 0.4825 0.4305 ${p_2}$ 0.1886 0.2273 0.4108 ${p_3}$ 0.0679 0.2903 0.3383 注:${p_x}$,${p_y}$,${p_{\textit{z}}}$为实际值;${p_1}$,${p_2}$,${p_3}$为理论值。 -
[1] 陈雁. 服装设计与工程学科发展趋势与关键议题[J]. 纺织学报, 2019, 40(1): 182-188Chen Y. Trends and key subjects of apparel design and engineering[J]. Journal of Textile Research, 2019, 40(1): 182-188 (in Chinese) [2] Schrimpf J, Lind M, Mathisen G. Work flow, material handling and initial part positioning in a multi-robot sewing cell[J]. IFAC-PapersOnLine, 2015, 48(19): 45-50 doi: 10.1016/j.ifacol.2015.12.008 [3] Ho C C, Tsai T R. Machine-vision-based servo control of a robotic sewing system[J]. Journal of Computational and Theoretical Nanoscience, 2012, 9(1): 45-49 [4] Denavit J, Hartenberg R S. A kinematic notation for lower-pair mechanisms based on matrices[J]. Journal of Applied Mechanics, 1995, 22(6): 215-221 [5] 杨振, 付庄, 管恩广, 等. M-Lattice模块机器人的运动学分析及构型优化[J]. 上海交通大学学报, 2017, 51(10): 1153-1159Yang Z, Fu Z, Guan E G, et al. The kinematic analysis and structure optimization of M-Lattice modular robot[J]. Journal of Shanghai Jiaotong University, 2017, 51(10): 1153-1159 (in Chinese) [6] 李亚玮, 黄晋英. 八自由度机械臂正运动学及工作空间分析[J]. 机械传动, 2016, 40(4): 94-96.Li Y W, Huang J Y. Analysis of the forward kinematics and workspace of 8-DOF manipulator[J]. Journal of Mechanical Transmission, 2016, 40(4): 94-96 (in Chinese). [7] 吕世增, 张大卫, 刘海年. 基于吴方法的6R机器人逆运动学旋量方程求解[J]. 机械工程学报, 2010, 46(17): 35-41 doi: 10.3901/JME.2010.17.035Lv S Z, Zhang D W, Liu H N. Solution of screw equation for inverse kinematics of 6R robot based on Wu's method[J]. Journal of Mechanical Engineering, 2010, 46(17): 35-41 (in Chinese) doi: 10.3901/JME.2010.17.035 [8] Heo J M, Choi S H, Park K S. Workspace analysis of a 6-DOF cable-driven parallel robot considering pulley bearing friction under ultra-high acceleration[J]. Microsystem Technologies, 2017, 23(7): 2615-2627 doi: 10.1007/s00542-016-3025-x [9] 裴九芳, 许德章, 王海. 基于旋量理论的三指机器人灵巧手逆运动学分析[J]. 中国机械工程, 2017, 28(24): 2975-2980 doi: 10.3969/j.issn.1004-132X.2017.24.013Pei J F, Xu D Z, Wang H. Inverse kinematics analyses of 3-finger robot dexterous hand based on screw theory[J]. China Mechanical Engineering, 2017, 28(24): 2975-2980 (in Chinese) doi: 10.3969/j.issn.1004-132X.2017.24.013 [10] 田勇, 王洪光, 潘新安, 等. 一种协作机器人工作空间灵活度的求解方法[J]. 机器人, 2019, 41(3): 298-306Tian Y, Wang H G, Pan X A, et al. A solving method for the workspace dexterity of collaborative robot[J]. Robot, 2019, 41(3): 298-306 (in Chinese) [11] Cao Y, Qi S P, Lu K, et al. An integrated method for workspace computation of robot manipulator[C]//Proceedings of 2009 International Joint Conference on Computational Sciences and Optimization. Sanya: IEEE, 2009: 309-312. [12] Bottur D, Martelli S, Fiorini P. Ageometric method for robot workspace computation[C]//Proceedings of the 11th International Conference on Autonomous Robots and System, Verona. Verona: Verona University Publications, 2003: 17-22. [13] 徐振邦, 赵智远, 贺帅, 等. 机器人工作空间求解的蒙特卡洛法改进和体积求取[J]. 光学 精密工程, 2018, 26(11): 2703-2713 doi: 10.3788/OPE.20182611.2703Xu Z B, Zhao Z Y, He S, et al. Improvement of Monte Carlo method for robot workspace solution and volume calculation[J]. Optics and Precision Engineering, 2018, 26(11): 2703-2713 (in Chinese) doi: 10.3788/OPE.20182611.2703 [14] Chen Q C, Zhu S Q, Zhang X Q. Improved inverse kinematics algorithm using screw theory for a Six-DOF robot manipulator[J]. International Journal of Advanced Robotic Systems, 2015, 12(10) [15] 王晓磊, 金振林, 李晓丹, 等. 串并混联四足仿生机器人动力学建模与分析[J]. 农业机械学报, 2019, 50(4): 401-412.Wang X L, Jin Z L, Li X D, et al. Dynamic Modeling and Analysis of Serial-parallel Hybrid Quadruped Bionic Robot[J]. Transactions of the Chinese Society for Agricultural Machinery, 2019, 50(4): 401-412 (in Chinese). [16] 刘燕德, 王观田, 王均刚, 等. 水果无损采摘机械手工作空间分析及参数确定[J]. 农机化研究, 2019, 41(4): 12-17.Liu Y D, Wang G T, Wang J G, et al. Workspace analysis and parameter determination of fruit nondestructive picking manipulator[J]. Journal of Agricultural Mechanization Research, 2019, 41(4): 12-17 (in Chinese). -







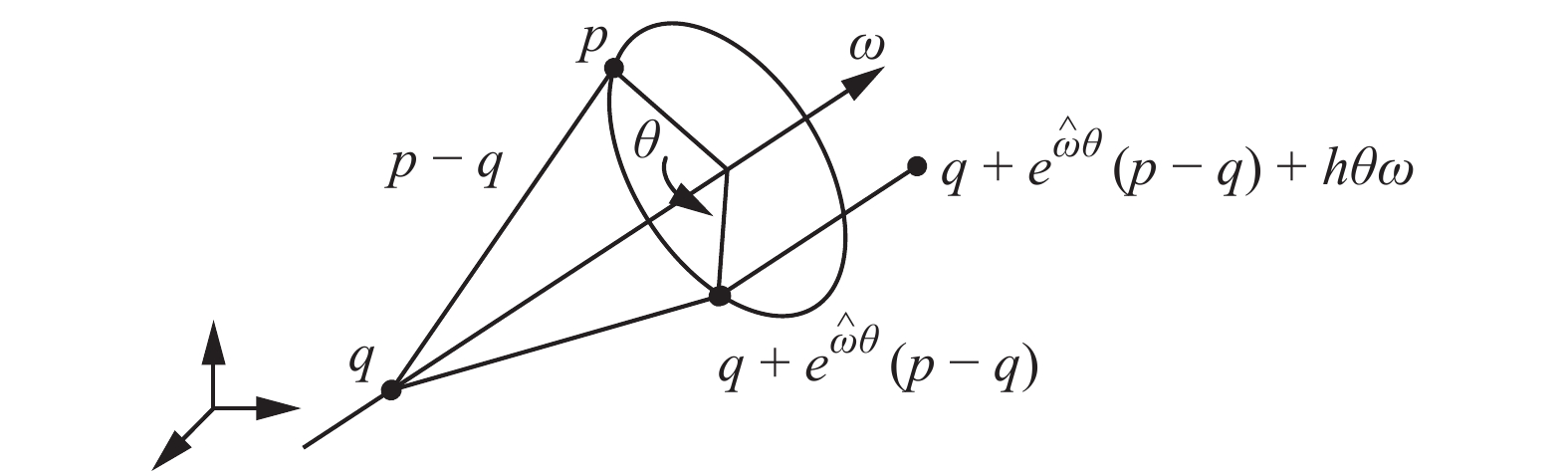
 下载:
下载: