Kinematics and Multi-objective Optimization of 4-URPU Multiple Locomotion Modes Mobile Parallel Mechanism
-
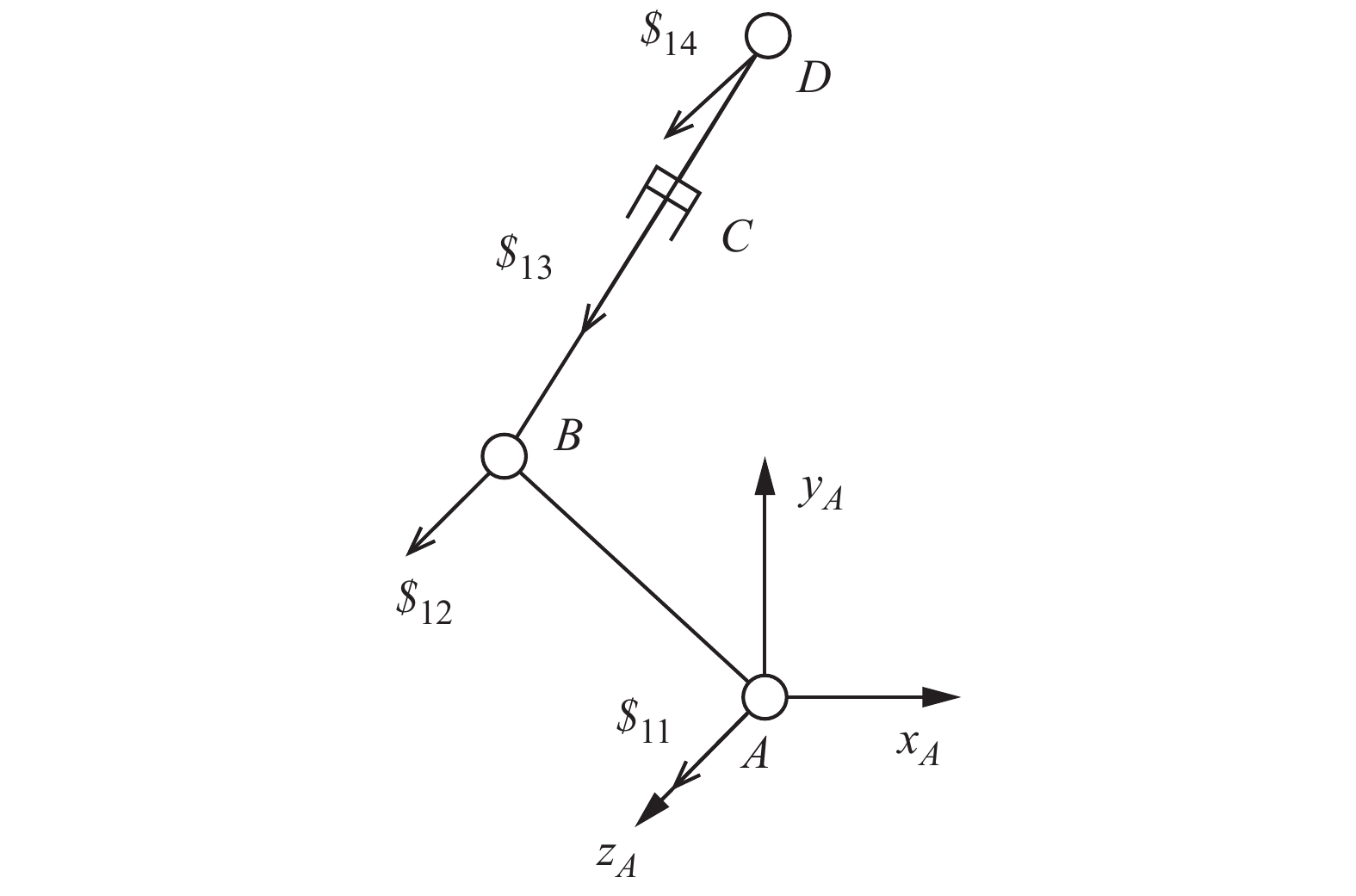
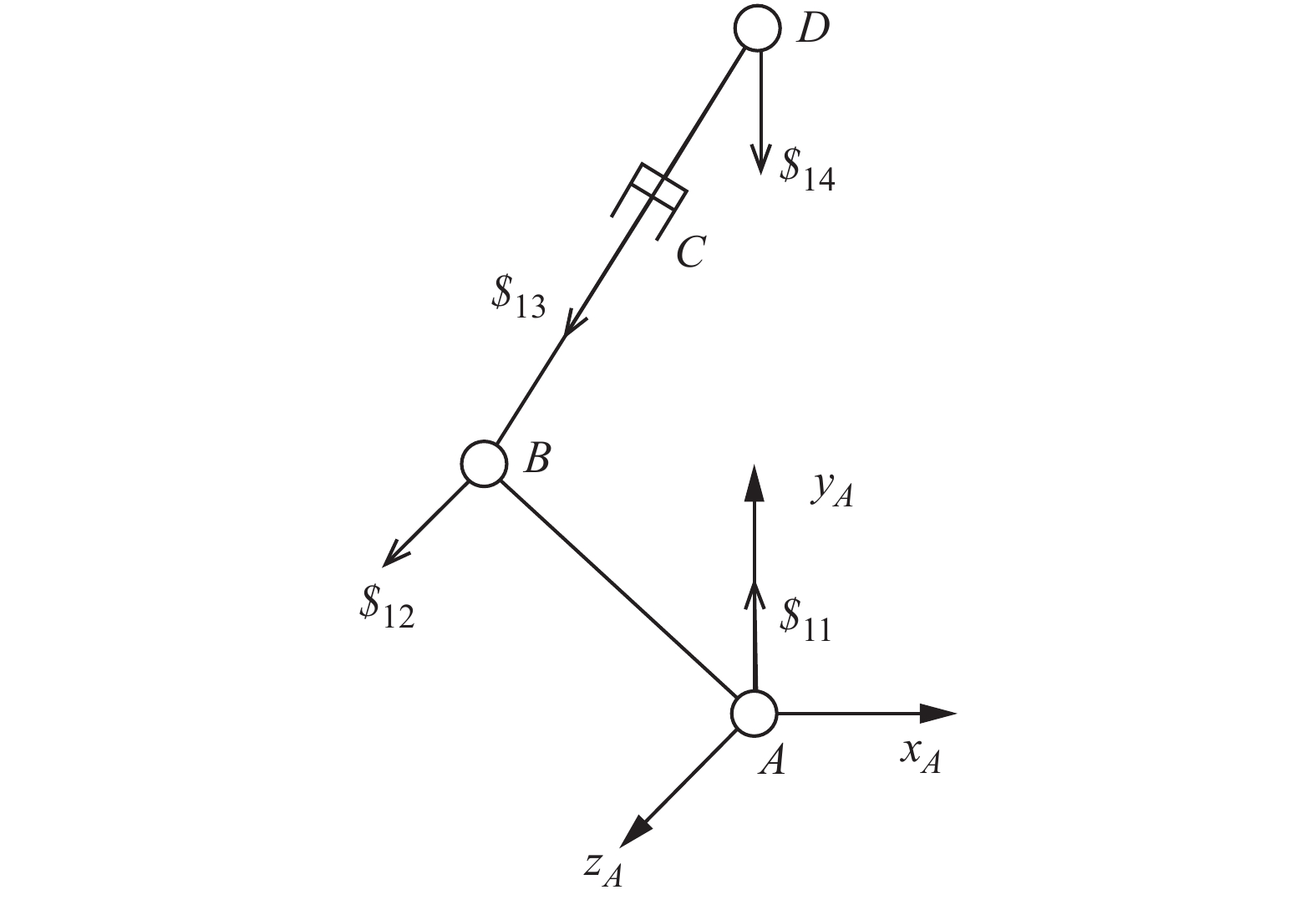
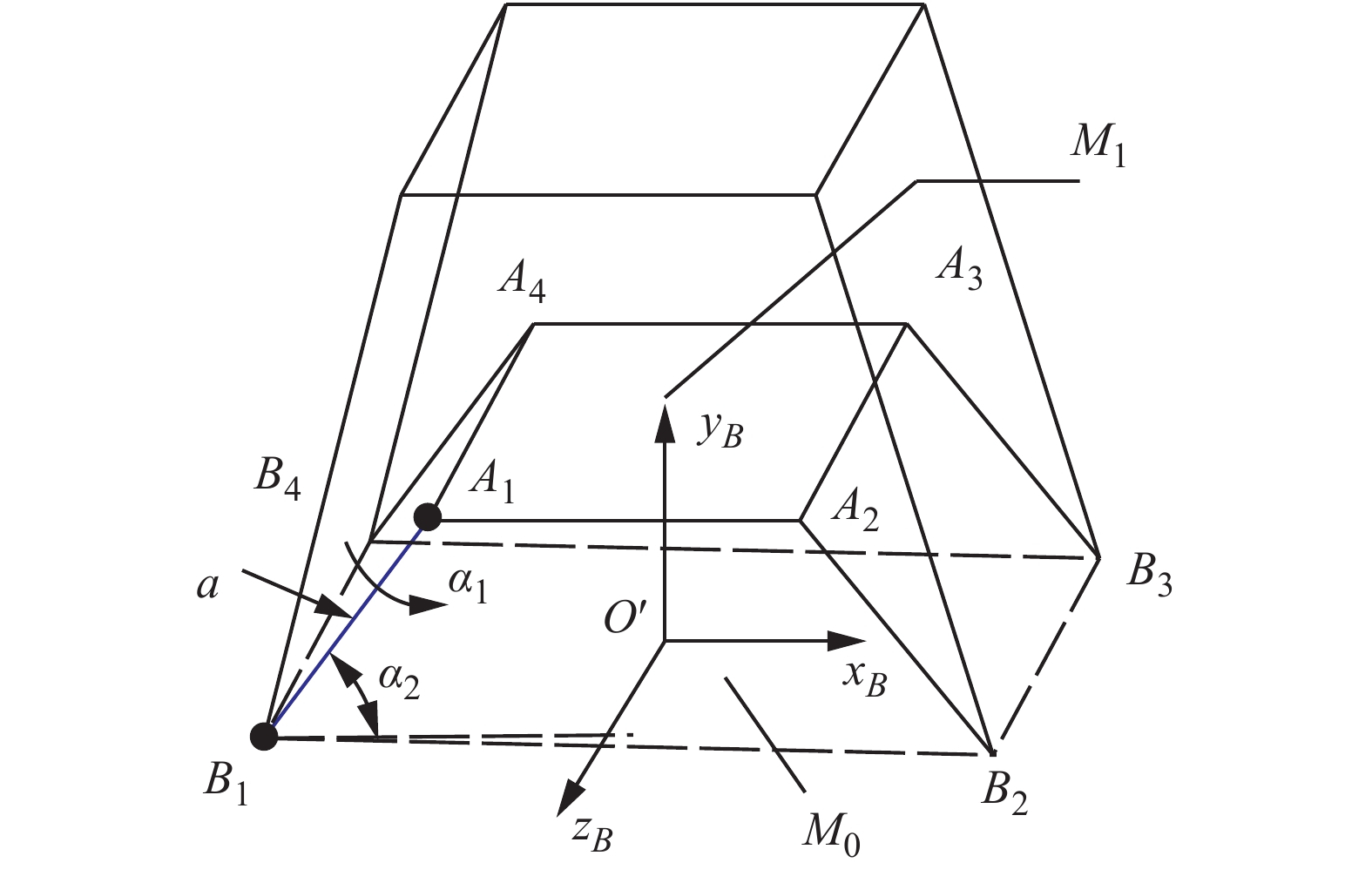
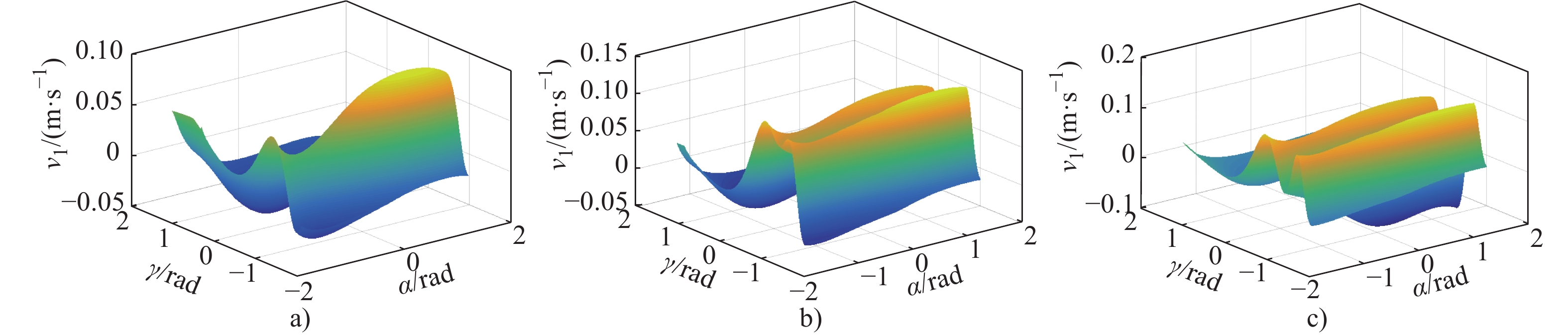
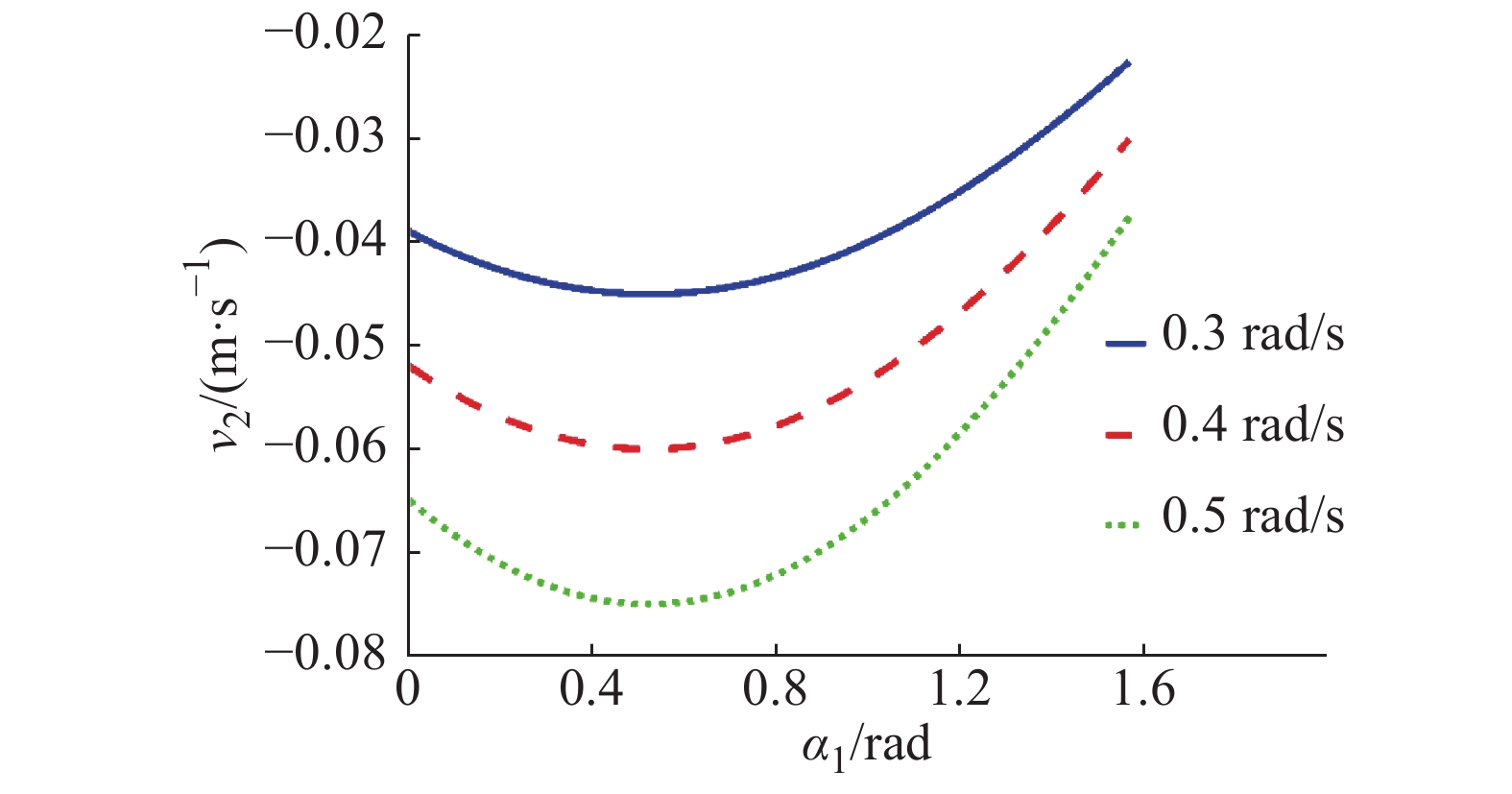
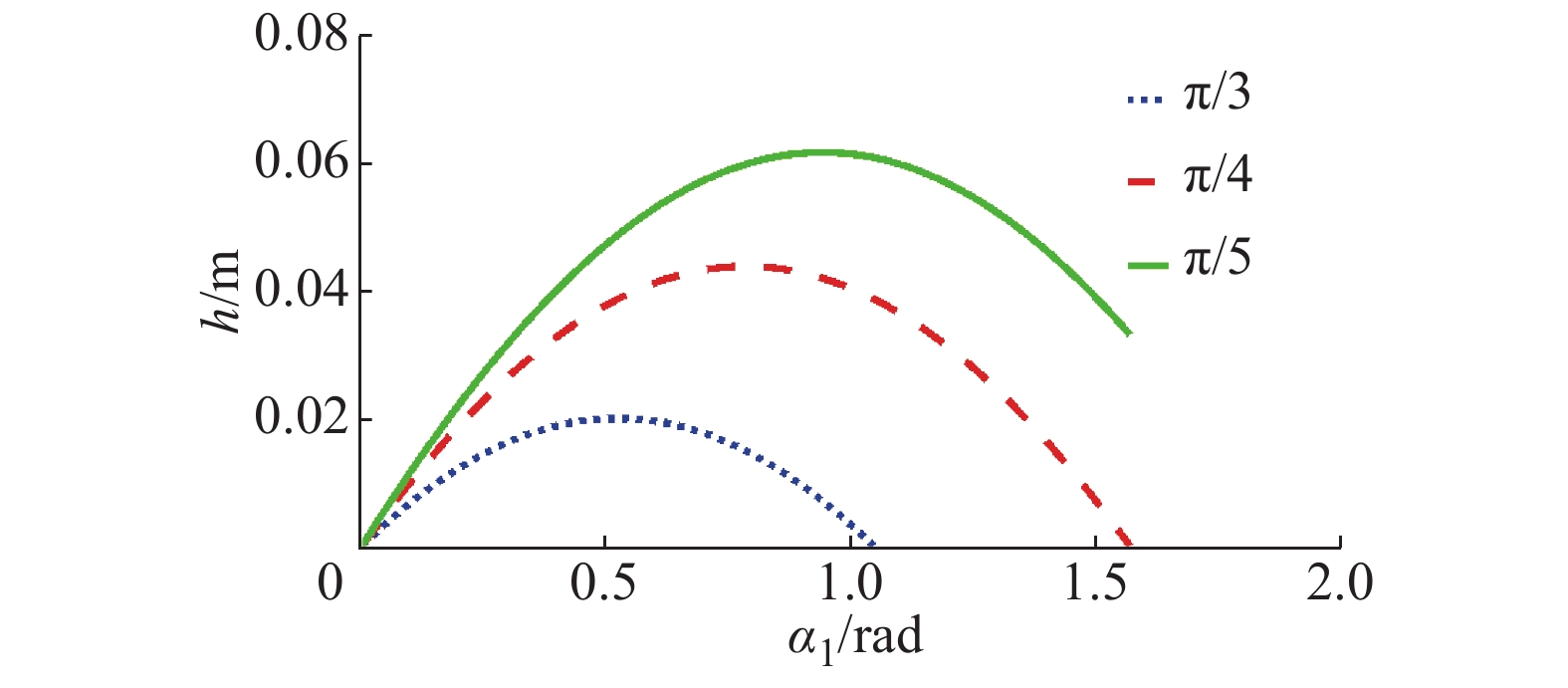
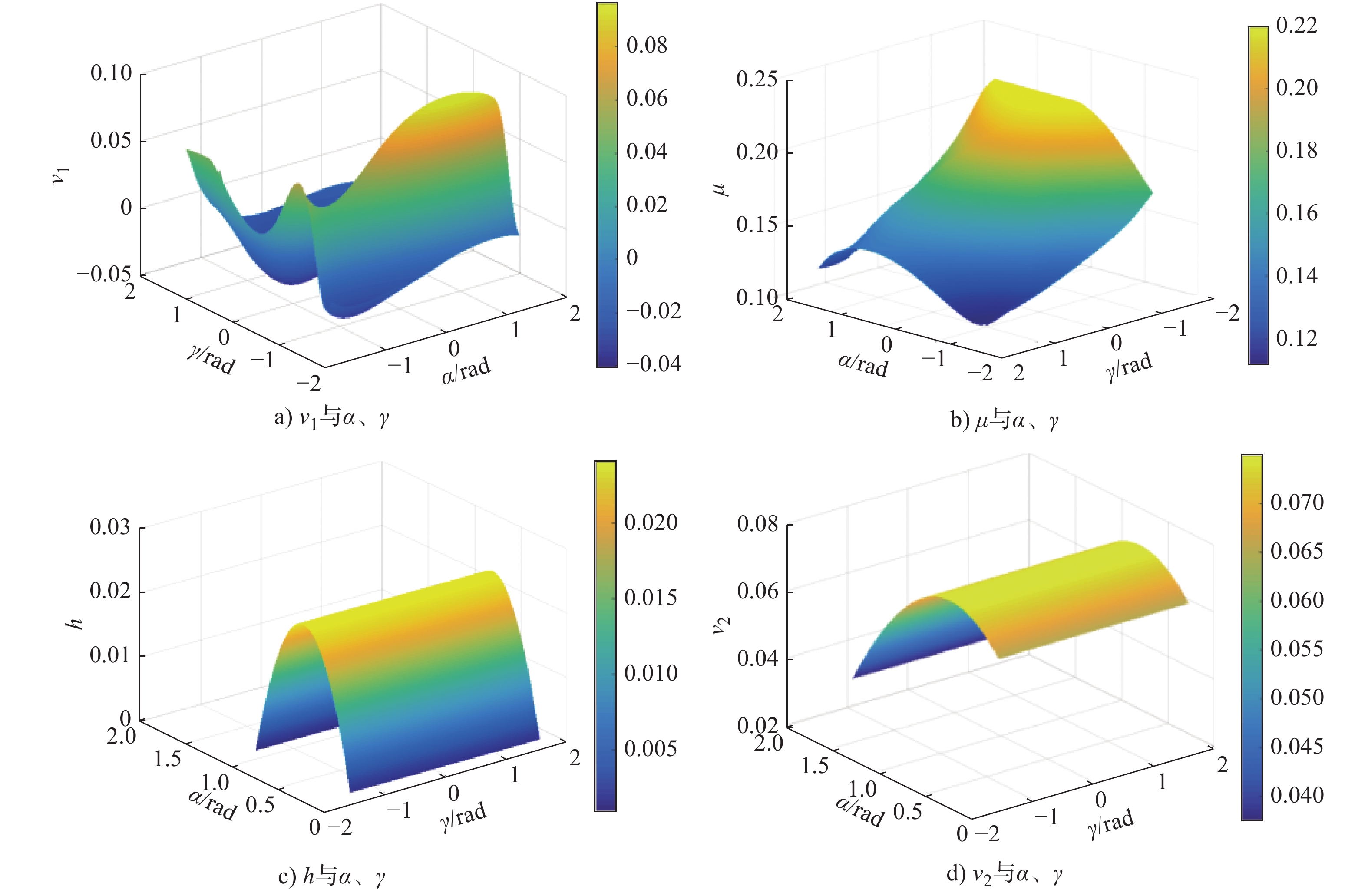
摘要: 为适应多重地形特征环境,本文提出一种集四足步行、蠕动和“全姿态”滚动等运动模式为一体的4-URPU多模式移动并联机构。利用螺旋理论分析了机构在各模式下的运动可行性,求解各模式下机构的位置解及速度雅可比矩阵,并建立多目标优化模型,得到一组相对最优解的集合。结果表明,行走过程中的速度性能指标的最大值低于机构在滚动过程中的速度性能指标,不同的工作环境有不同的最优解决方案。最后对机构进行样机试验,验证了该机构的理论正确性以及运动可行性。所提出的机构可应用于核电事故、野外、自然灾害等具有多重地形特征的地理环境中,有一定的应用前景。Abstract: To adapt to the multi-terrain environment, a 4-URPU multiple locomotion modes mobile parallel mechanism is proposed, which integrates three motion modes of quadruped walking, creeping and rolling. The kinematic feasibility of the mechanism in each mode is analyzed by the screw theory. The position solution and velocity Jacobian matrix of the mechanism in each mode are solved, and a multi-objective optimization model is established to obtain a set of relative optimal solutions. The results show that the maximum speed performance index in walking process is lower than that in rolling process, and there are different optimal solutions for different working environments. Finally, a prototype test is carried out to verify the theoretical correctness and kinematic feasibility of the mechanism. The proposed mechanism can be applied to geographic environments with multiple topographic features such as nuclear power accidents, field and natural disasters, and has a certain application prospect.
-
表 1 输入量
$ \alpha $ 、$ \beta$ 、$ \gamma $ 与机构稳定性关系输入量$\alpha $ 输入量$\beta $ 输入量$\gamma $ 稳定性 ${{\text{π}} / 3}$ $\left( { - {{\text{π}} / 5},{{\text{π}} / 2}} \right)$ $\left( { - {{\text{π}} / 5},{{\text{π}} / 2}} \right)$ 是 ${{\text{π}} / 3}$ $\left( { - {{\text{π}} / 2},{{ - {\text{π}} } / 5}} \right)$ $\left( { - {{\text{π}} / 2},{{ - {\text{π}} } / 5}} \right)$ 否 -
[1] 王晓芸. 轮腿复合式救援机器人机构分析与仿真[D]. 秦皇岛: 燕山大学, 2015.Wang X Y. Mechinical analysis and simulation of a novel wheel-leg hybrid rescue robot[D]. Qinhuangdao: Yanshan University, 2015 (in Chinese). [2] 杨帆, 吴贺利, 罗晨晖. 一种轮腿式越障机器人的设计与分析[J]. 机械传动, 2017, 41(5): 198-203Yang F, Wu H L, Luo C H. Design and analysis of a wheel-legged obstacle climbing robot[J]. Journal of Mechanical Transmission, 2017, 41(5): 198-203 (in Chinese) [3] Pan Y, Gao F, Qi C K, et al. Human-tracking strategies for a six-legged rescue robot based on distance and view[J]. Chinese Journal of Mechanical Engineering, 2016, 29(2): 219-230 doi: 10.3901/CJME.2015.1212.146 [4] 田耀斌. 多模式移动连杆机构理论研究[D]. 北京: 北京交通大学, 2015.Tian Y B. Research on theories of mobile linkage with multiple locomotion modes[D]. Beijing: Beijing Jiaotong University, 2015 (in Chinese). [5] Wang N Y, Fang Y F, Zhang D. A spatial single loop kinematotropic mechanism used for biped/wheeled switchable robots[J]. International Journal of Mechanics and Materials in Design, 2015, 11(3): 287-299 doi: 10.1007/s10999-014-9274-x [6] 苗智英, 李瑞琴, 张启升, 等. 3-PUU轮腿式移动机器人的步态与稳定性分析[J]. 机械传动, 2018, 42(3): 90-93Miao Z Y, Li R Q, Zhang Q S, et al. Gait and stability analysis of 3-PUU wheel-legged mobile robot[J]. Journal of Mechanical Transmission, 2018, 42(3): 90-93 (in Chinese) [7] 张成军, 李艳文. 一种基于3-RPC并联机构的新型步行机器人[J]. 机械工程学报, 2011, 47(15): 25-30 doi: 10.3901/JME.2011.15.025Zhang C J, Li Y W. A new walking robot based on 3-RPC parallel mechanism[J]. Journal of Mechanical Engineering, 2011, 47(15): 25-30 (in Chinese) doi: 10.3901/JME.2011.15.025 [8] Xi D, Gao F. Type synthesis of walking robot legs[J]. Chinese Journal of Mechanical Engineering, 2018, 31: 15 doi: 10.1186/s10033-018-0216-7 [9] 黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社, 2006.Huang Z, Zhao Y S, Zhao T S. Advanced spatial mechanism[M]. Beijing: Higher Education Press, 2006 (in Chinese). [10] 王孝义, 秦建恒, 邱晗, 等. 基于ZMP的类双足步行机构行走稳定性控制[J]. 机械科学与技术, 2014, 33(6): 802-806Wang X Y, Qin J H, Qiu H, et al. Walking stability control of a new biped-imitating walking mechanism based on ZMP[J]. Mechanical Science and Technology for Aerospace Engineering, 2014, 33(6): 802-806 (in Chinese) [11] Yi S. Reliable gait planning and control for miniaturized quadruped robot pet[J]. Mechatronics, 2010, 20(4): 485-495 doi: 10.1016/j.mechatronics.2010.04.006 [12] Vukobratovic M, Borovac B, Surdilovic D. Zero-moment point: proper interpretation and new applications[C]//Proceedings of IEEE-RAS International Conference on Humanoid Robots. Tokyo: Waseda University, 2001: 237-244. [13] 葛为民, 张华瑾, 王肖锋, 等. 自重构机器人变形过程运动学分析及越障仿真[J]. 中国机械工程, 2014, 25(19): 2608-2613, 2619 doi: 10.3969/j.issn.1004-132X.2014.19.011Ge W M, Zhang H J, Wang Y F, et al. Kinematics analysis of self-reconfigurable robot during deformation process and simulation of obstacle climbing[J]. China Mechanical Engineering, 2014, 25(19): 2608-2613, 2619 (in Chinese) doi: 10.3969/j.issn.1004-132X.2014.19.011 [14] 余联庆, 枚元元, 李琳, 等. 闭链弓形五连杆越障能力分析与运动规划[J]. 机械工程学报, 2017, 53(7): 69-75 doi: 10.3901/JME.2017.07.069Yu L Q, Mei Y Y, Li Lin, et al. Capability analysis and motion planning for obstacle negotiation of a closed five-bow-shaped-bar linkage[J]. Journal of Mechanical Engineering, 2017, 53(7): 69-75 (in Chinese) doi: 10.3901/JME.2017.07.069 [15] Li Y Z, Yao Y A, He Y Y. Design and analysis of a multi-mode mobile robot based on a parallel mechanism with branch variation[J]. Mechanism and Machine Theory, 2018, 130: 276-300 doi: 10.1016/j.mechmachtheory.2018.07.018 [16] Zhang D, Gao Z. Forward kinematics, performance analysis, and multi-objective optimization of a bio-inspired parallel manipulator[J]. Robotics and Computer-Integrated Manufacturing, 2012, 28(4): 484-492 doi: 10.1016/j.rcim.2012.01.003 [17] Kelaiaia R, Company O, Zaatri A. Multiobjective optimization of a linear Delta parallel robot[J]. Mechanism and Machine Theory, 2012, 50: 159-178 doi: 10.1016/j.mechmachtheory.2011.11.004 [18] Russo M, Herrero S, Altuzarra O, et al. Kinematic analysis and multi-objective optimization of a 3-UPR parallel mechanism for a robotic leg[J]. Mechanism and Machine Theory, 2018, 120: 192-202 doi: 10.1016/j.mechmachtheory.2017.10.004 [19] 池腾腾. 并联机构2-RPU/SPR动平台的多目标优化与稳健性研究[D]. 河北邯郸: 河北工程大学, 2017.Chi T T. Multi-objective optimization and robustness study for a moving platform of 2-RPU/SPR parallel mechanism[D]. Hebei Handan: Hebei University of Engineering, 2017 (in Chinese). -








 下载:
下载: