Study on Ultrasonic Dry Coupling Performance of Rough Contact Interface
-
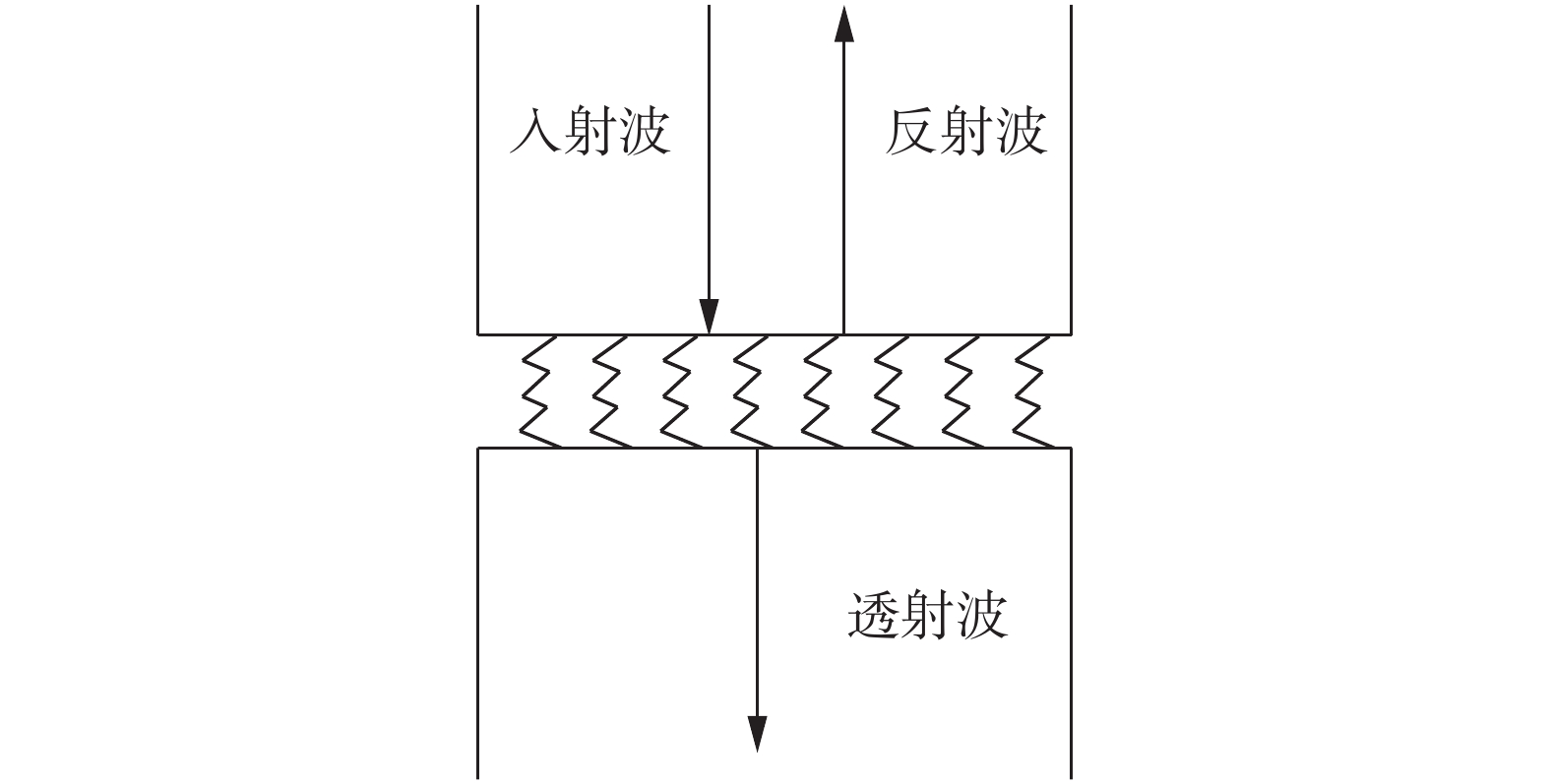
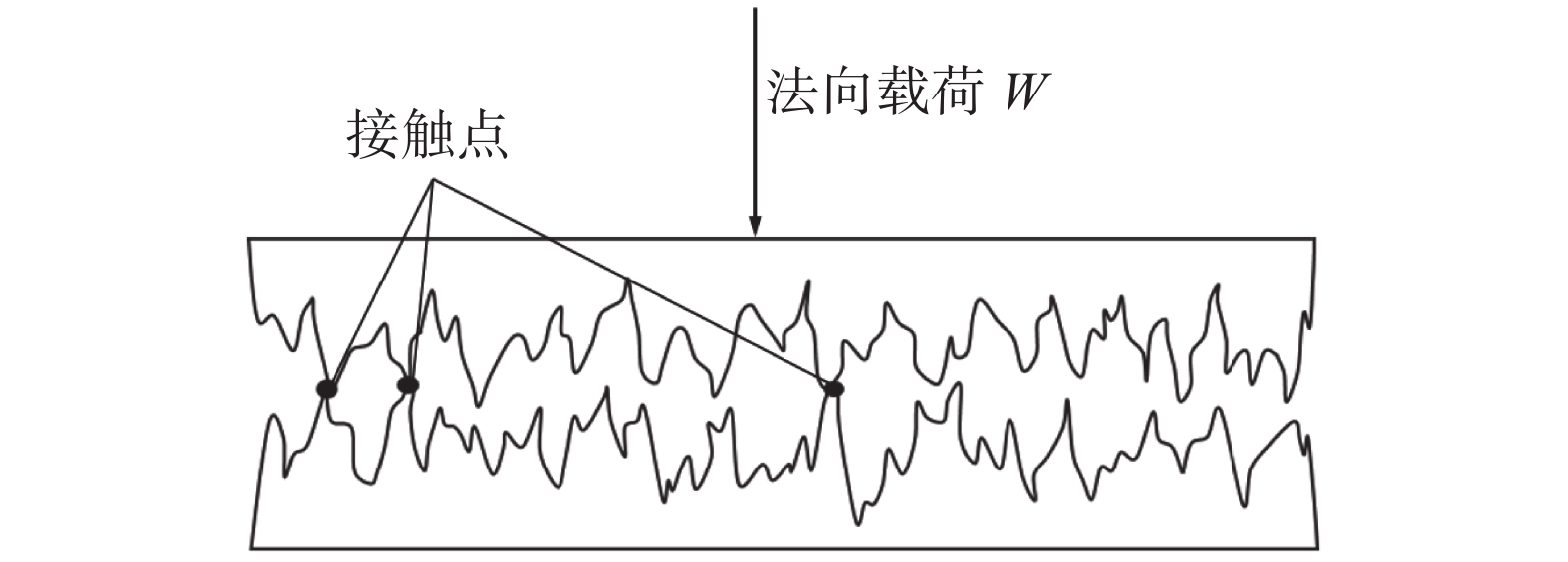
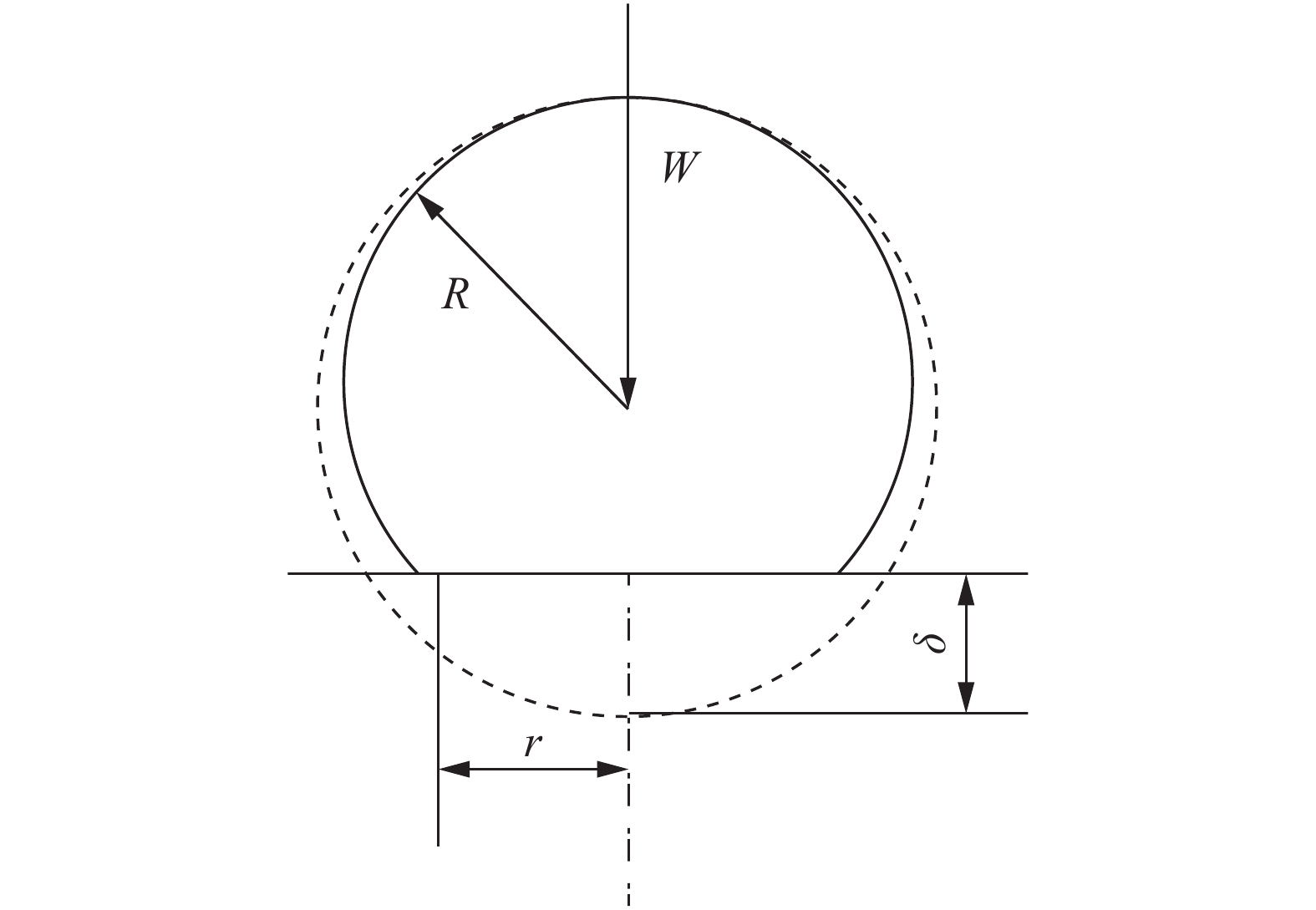
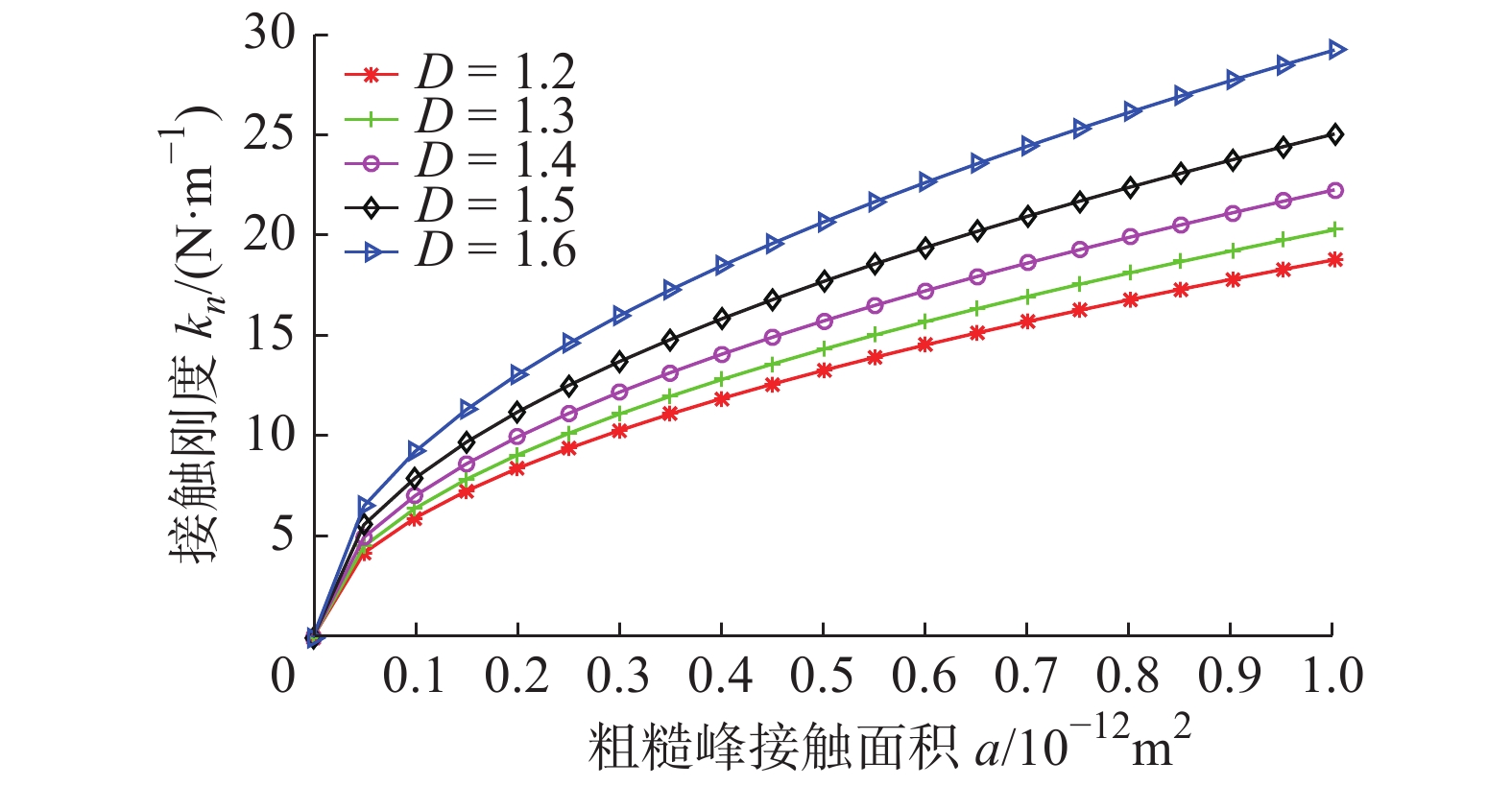
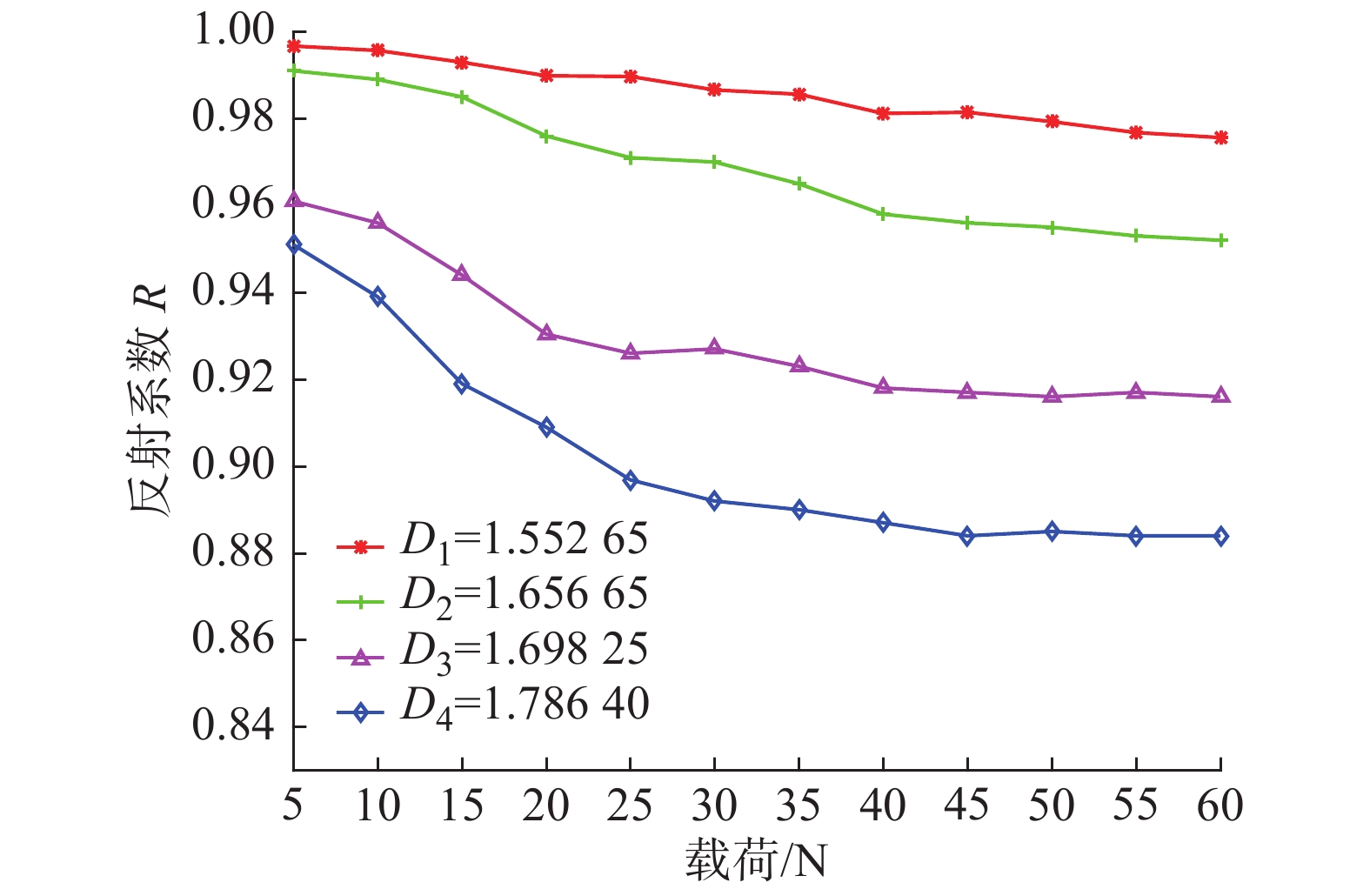
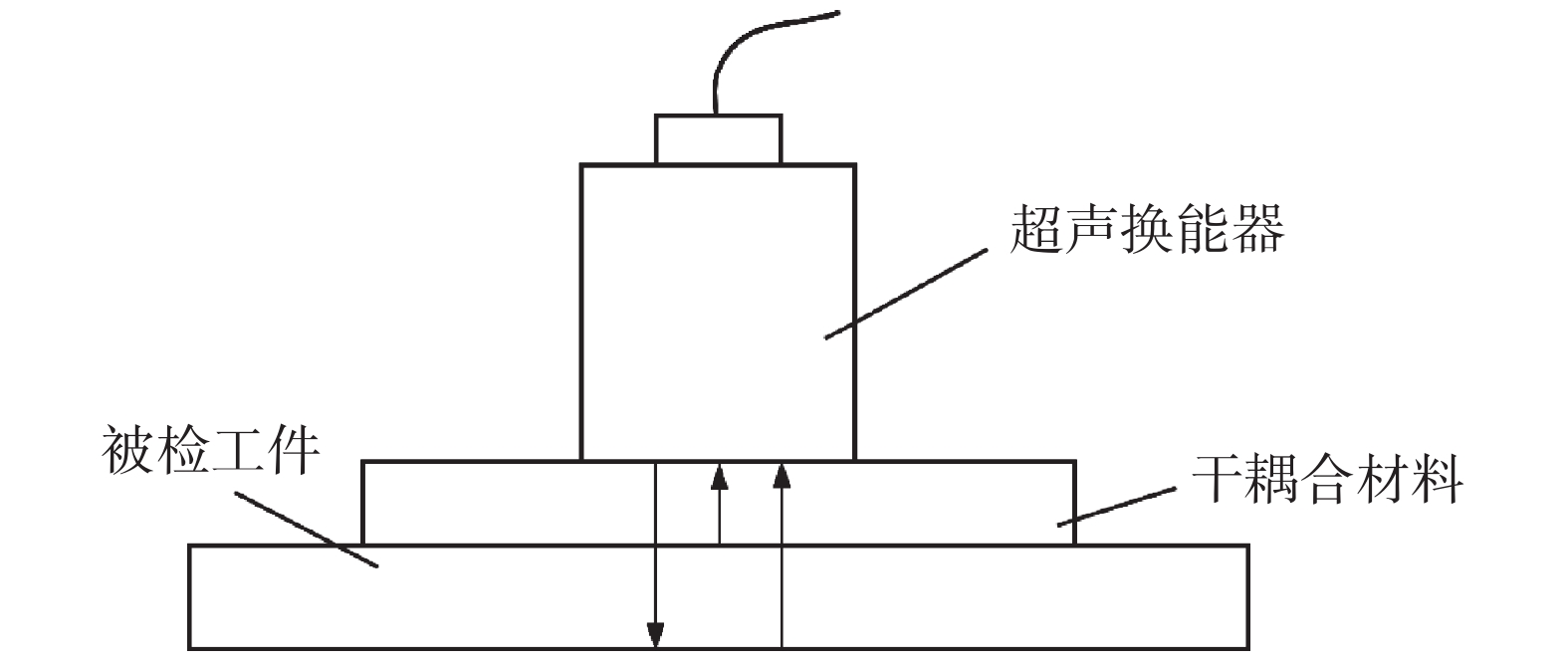
摘要: 为提高粗糙接触界面的声耦合性能,对超声波与粗糙界面间的相互作用进行研究。通过界面分形模型的建立,得到含分形参数的接触刚度表达式,并结合界面声学模型分析不同耦合条件下声反射系数的变化;搭建超声干耦合实验平台,通过实验测得粗糙铝板表面轮廓,利用结构函数法对分形维数进行测定,并对不同分形维数的粗糙铝板进行受压条件下的反射系数测量。结果表明:对粗糙接触界面施加一定载荷有利于超声波在界面处的传播,且分形维数较大的粗糙铝板达到良好声耦合效果所需的载荷更小,更便于超声干耦合检测的实施。Abstract: In order to improve the ultrasonic dry-coupled performance of rough contact interface, the interaction between the ultrasonic wave and the rough interface is studied. The contact stiffness expression with fractal parameters is obtained by establishing the interface fractal model, and the change in acoustic reflection coefficient under different coupling conditions is analyzed by combining the interface acoustic model. The ultrasonic dry-coupling experimental platform is established to measure the surface profile of rough aluminum plate. The fractal dimension is measured with structural function method, and the reflection coefficient of rough aluminum plate with different fractal dimension under pressure is measured. The results show that the coupling performance can be improved by increasing the pressure between the solid surfaces, and the rough aluminum plate with larger fractal dimension needs less load to achieve good acoustic coupling effect, which is more convenient for the implementation of ultrasonic dry coupling detection.
-
Key words:
- dry coupling /
- reflection coefficient /
- rough contact interface /
- fractal model
-
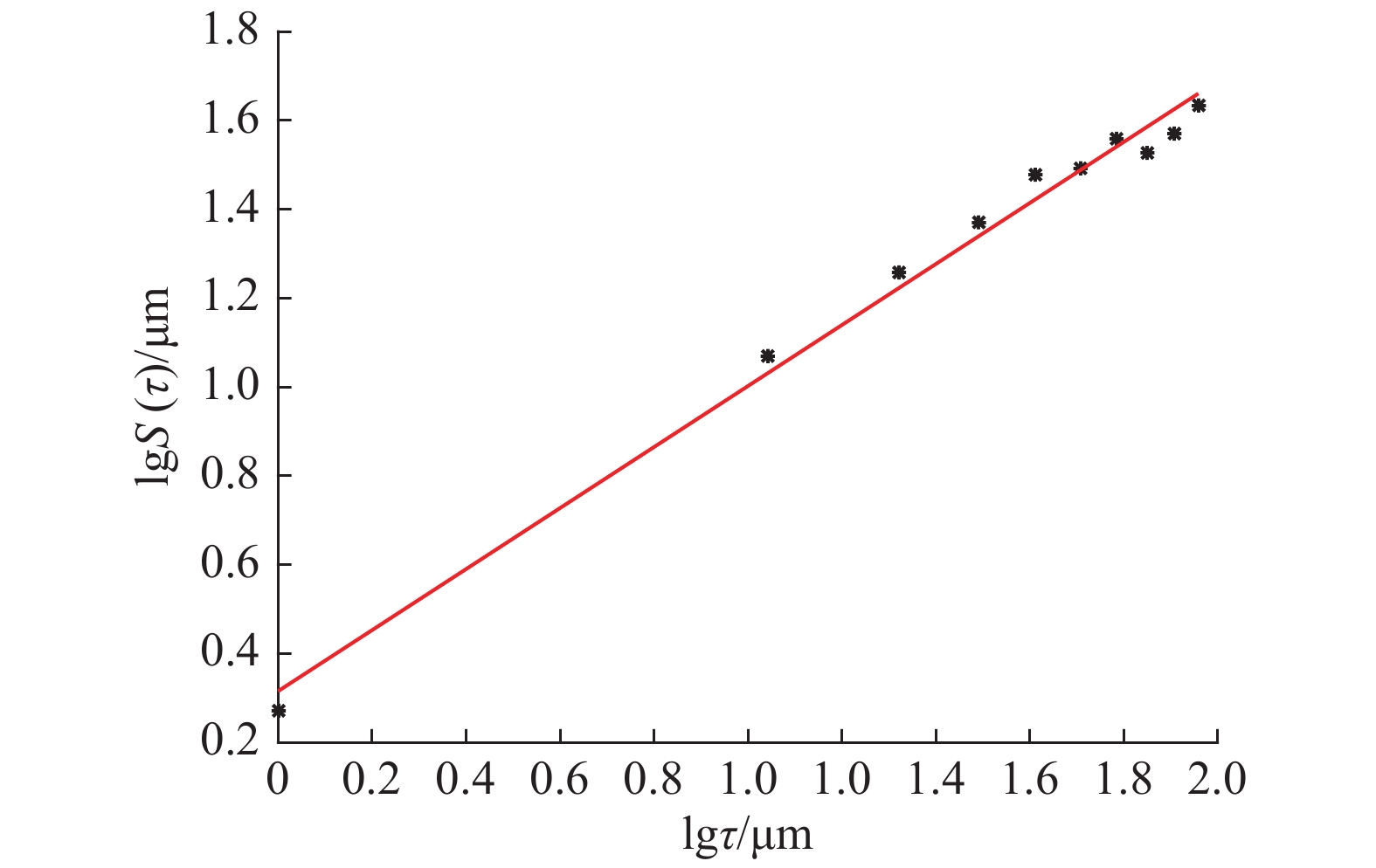
表 1 不同粗糙度铝板的分形维数
铝板
试样回归直线
斜率粗糙轮廓
分形维数D铝板试样
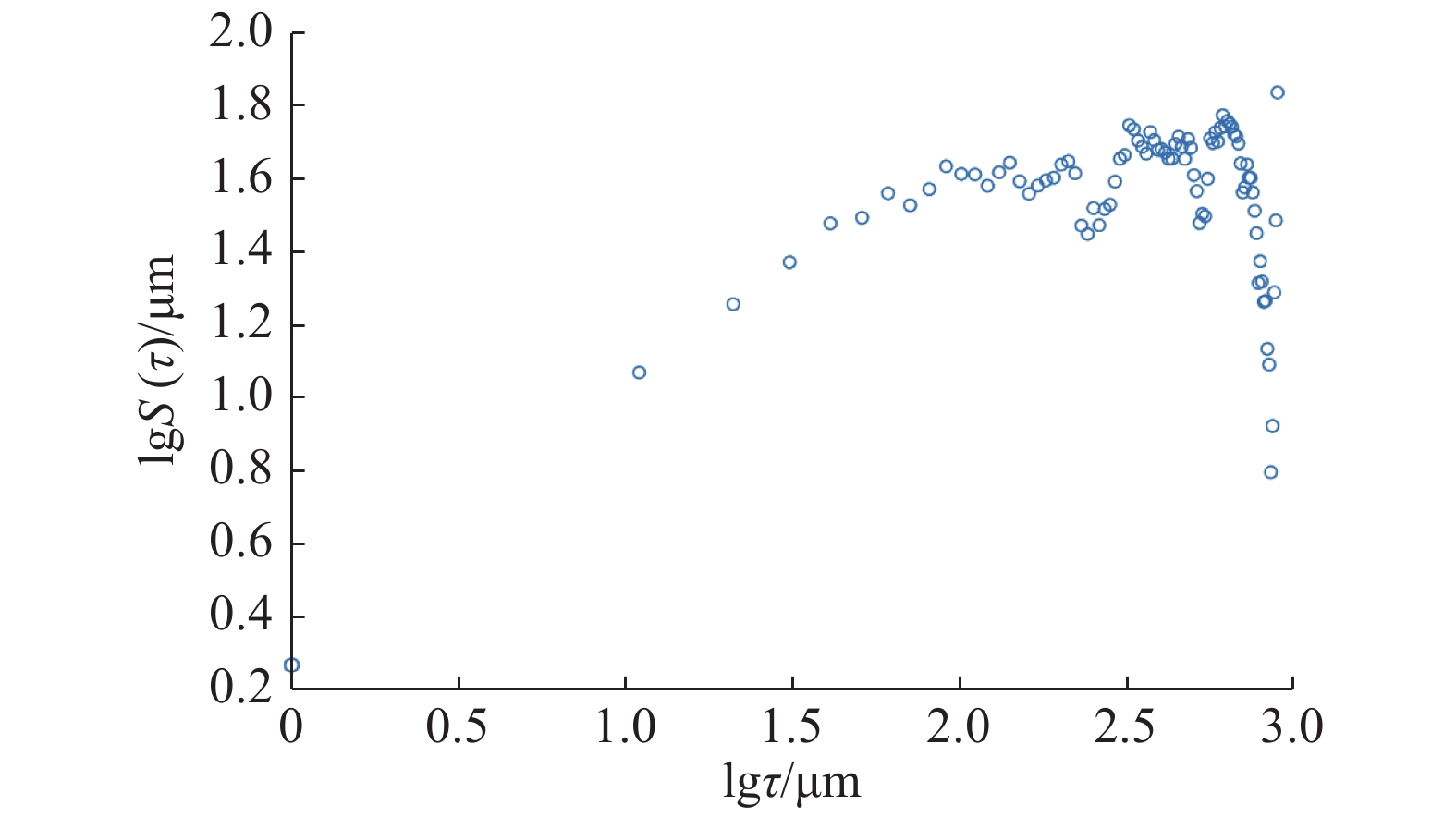
粗糙度/μm1 0.686 7 1.656 65 2.504 2 0.603 5 1.698 25 1.968 3 0.427 2 1.786 40 0.979 4 0.894 7 1.552 65 4.181 -
[1] 艾春安, 曾一平, 李剑, 等. 复合材料干耦合声学检测技术的发展与应用[J]. 无损检测, 2012, 34(9): 50-54Ai C A, Zeng Y P, Li J, et al. Development and application of dry-coupled acoustic detection technology for composites[J]. Nondestructive Testing, 2012, 34(9): 50-54 (in Chinese) [2] 穆洪彬, 吴朝军, 吴晨, 等. 干耦合超声检测技术在某火箭发动机喷管在役检测中的应用[J]. 无损检测, 2013, 35(6): 40-43Mu H B, Wu Z J, Wu C, et al. Application of dry coupling ultrasonic detecting technology for the rocket engine nozzle[J]. Nondestructive Testing, 2013, 35(6): 40-43 (in Chinese) [3] 周娥, 王晓勇. 干耦合穿透法在橡胶复合材料无损检测中的应用研究[J]. 航天制造技术, 2017, (2): 47-49 doi: 10.3969/j.issn.1674-5108.2017.02.013Zhou E, Wang X Y. Application of dry coupled penetration method in nondestructive testing of rubber composites[J]. Aerospace Manufacturing Technology, 2017, (2): 47-49 (in Chinese) doi: 10.3969/j.issn.1674-5108.2017.02.013 [4] Robinson A M, Drinkwater B W, Allin J. Dry-coupled low-frequency ultrasonic wheel probes: application to adhesive bond inspection[J]. NDT & E International, 2003, 36(1): 27-36 [5] 田志亮, 孙守林, 邱俊, 等. 考虑支撑结构及螺栓连接的变桨轴承强度分析[J]. 机械设计与制造, 2018, (5): 127-130 doi: 10.3969/j.issn.1001-3997.2018.05.038Tian Z L, Sun S L, Qiu J, et al. Strength analysis for pitch bearing considered the support structure and bolt connection[J]. Machinery Design & Manufacture, 2018, (5): 127-130 (in Chinese) doi: 10.3969/j.issn.1001-3997.2018.05.038 [6] 何清, 刘更, 佟瑞庭. 二维多粗糙峰粘着接触问题的有限元分析[J]. 机械科学与技术, 2010, 29(10): 1306-1310He Q, Liu G, Tong R T. Finite element analysis of multi-asperity adhesion contact problems[J]. Mechanical Science and Technology for Aerospace Engineering, 2010, 29(10): 1306-1310 (in Chinese) [7] 王立华, 杨竹, 陆梓, 等. 机械结合面微观接触弹流润滑数值分析[J]. 机械科学与技术, 2016, 35(10): 1531-1537Wang L H, Yang Z, Lu Z, et al. Numerical analysis on micro-elastohydro dynamic lubrication of machine joint surfaces[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(10): 1531-1537 (in Chinese) [8] 成雨, 原园, 甘立, 等. 尺度相关的分形粗糙表面弹塑性接触力学模型[J]. 西北工业大学学报, 2016, 34(3): 485-492 doi: 10.3969/j.issn.1000-2758.2016.03.020Cheng Y, Yuan Y, Gan L, et al. The elastic-plastic contact mechanics model related scale of rough surface[J]. Journal of Northwestern Polytechnical University, 2016, 34(3): 485-492 (in Chinese) doi: 10.3969/j.issn.1000-2758.2016.03.020 [9] 原园, 张利华, 徐颖强. 粗糙球形表面的分形接触力学模型[J]. 西安交通大学学报, 2019, 53(5): 176-186Yuan Y, Zhang L H, Xu Y Q. Mechanical model of contact between a sphere-based fractal rough surface and a rigid flat surface[J]. Journal of Xi'an Jiaotong University, 2019, 53(5): 176-186 (in Chinese) [10] Johnson K L. Contact mechanics[M]. Cambridge: Cambridge University Press, 1985 [11] Greenwood J A, Williamson J B P P. Contact of nominally flat surfaces[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1966, 295(1442): 300-319 [12] Sayles R S, Thomas T R. Surface topography as a nonstationary random process[J]. Nature, 1978, 271(5644): 431-434 doi: 10.1038/271431a0 [13] Majumdar A, Tien C L. Fractal characterization and simulation of rough surfaces[J]. Wear, 1990, 136(2): 313-327 doi: 10.1016/0043-1648(90)90154-3 [14] 黄健萌, 戴煜宸, 林有希, 等. 纳观分形粗糙表面的建模分析[J]. 摩擦学学报, 2018, 38(2): 138-144Huang J M, Dai Y C, Lin Y X, et al. Modeling and analysis of fractal rough nanoscale surfaces[J]. Tribology, 2018, 38(2): 138-144 (in Chinese) [15] Tattersall H G. The ultrasonic pulse-echo technique as applied to adhesion testing[J]. Journal of Physics D: Applied Physics, 1973, 6(7): 819-832 doi: 10.1088/0022-3727/6/7/305 [16] Majumdar A, Bhushan B. Fractal model of elastic-plastic contact between rough surfaces[J]. Journal of Tribology, 1991, 113(1): 1-11 doi: 10.1115/1.2920588 [17] Mandelbrot B B. Stochastic models for the Earth's relief, the shape and the fractal dimension of the coastlines, and the number-area rule for islands[J]. Proceedings of the National Academy of Sciences of the United States of America, 1975, 72(10): 3825-3828 doi: 10.1073/pnas.72.10.3825 [18] 葛世荣, 朱华. 摩擦学的分形[M]. 北京: 机械工业出版社, 2005.Ge S R, Zhu H. Fractal in tribology[M]. Beijing: China Machine Press, 2005 (in Chinese) [19] 张学良. 机械结合面动态特性及应用[M]. 北京: 中国科学技术出版社, 2002Zhang X L. The dynamic characteristics of machine joint surfaces and its application[M]. Beijing: China Science and Technology Press, 2002 (in Chinese) [20] Connolly R, Thornley R H. Determining the normal stiffness of joint faces[J]. Journal of Engineering for Industry, 1968, 90(1): 97-106 doi: 10.1115/1.3604614 [21] 王鹏程. 基于分形理论的结合面接触特性分析[D]. 昆明: 昆明理工大学, 2015Wang P C. The characteristic analysis of joint surface contact based on fractal theory[D]. Kunming: Kunming University of Science and Technology, 2015 (in Chinese) [22] 郑晖, 林树青. 超声检测[M]. 2版. 北京: 中国劳动社会保障出版社, 2008Zheng H, Lin S Q. The second edition of ultrasonic testing[M]. 2nd ed. Beijing: China Labor and Social Security Press, 2008 (in Chinese) -







 下载:
下载: