Nonprobability-based Design Optimization Considering Reliability Robustness for Structures
-
摘要: 传统基于概率模型可靠性设计优化(Reliability-based design optimization,RBDO)通过制定结构性能的概率约束,使得设计结果符合可靠性要求。然而,在参数信息缺乏时,准确的参数概率密度函数难以获取,且在不确定性因素影响下可靠性的稳健性并未被考虑。在参数信息缺乏的情况下,本文中利用非概率凸模型去有效地度量参数的不确定性。根据非概率可靠性分析理论,将极限状态函数进行泰勒展开,利用非概率可靠性指标的灵敏度分析,建立非概率可靠性的鲁棒性指标。将非概率可靠性设计优化与非概率鲁棒性设计集成到统一的设计模型中,结合SORA(Sequential optimization and reliability assessment)方法和微型多目标遗传算法进行求解。最后,通过两个工程算例分析结果,表明所提优化模型的可行性。Abstract: The traditional reliability-based design optimization (RBDO), which is based on probabilistic model, can guarantee the reliability of structure by formulating probabilistic constraints. However, it is difficult to obtain the accurate probability density function of parameter when the parameter information is limited. Meanwhile, the reliability robustness is not fully considered in optimization. In this paper, the non-probabilistic convex model is utilized to measure the uncertainty of parameter with insufficient information. Based on the theory of non-probabilistic reliability analysis, Taylor expansion is conducted for the limit-state function, and the robustness index of non-probabilistic reliability is formulated through the sensitivity analysis of non-probabilistic reliability index. Then, a unified design framework integrating the reliability-based design with robust design is established. The optimization can be implemented efficiently by combining the sequential optimization and reliability assessment (SORA) and the micro multi-objective genetic algorithm. Two engineering applications are presented to demonstrate the effectiveness of the optimization model.
-
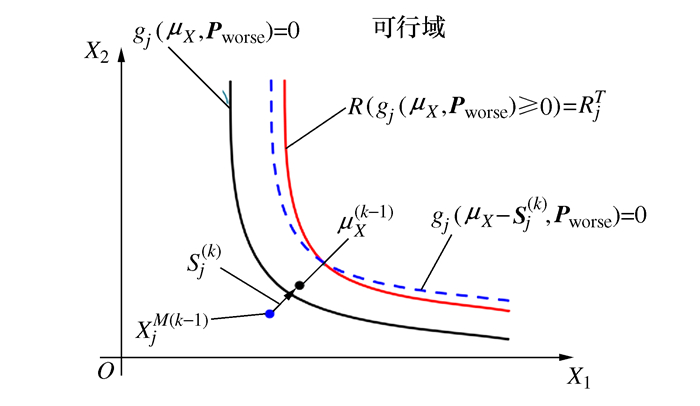
图 3 SORA方法中概率约束的移动矢量[23]
图 4 椭球凸模型的空间转换[4]
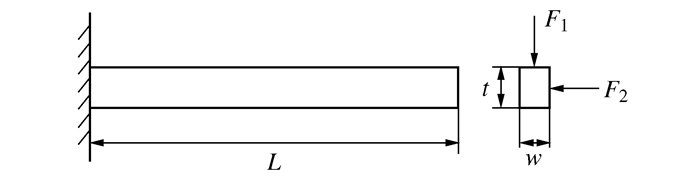
图 6 悬臂梁结构图[23]
图 8 智能手环结构图[23]
图 9 智能手环温热性能有限元模型[23]
表 1 数值算例1的部分优化解
序号 设计点 f1 增加 f2 减少 β1 β2 1 [2.70, 3.91] 10.55 - 16.10 - 3.00 3.55 2 [3.41, 3.27] 11.14 5.64% 14.55 9.66% 3.17 3.15 3 [3.66, 3.15] 11.55 9.47% 14.15 12.11% 3.36 3.01 4 [3.73, 3.14] 11.71 11.06% 14.06 12.66% 3.48 .04 5 [3.90, 3.10] 12.09 14.67% 13.86 13.93% 3.71 3.08 6 [4.11, 3.04] 12.49 18.42% 13.63 15.34% 3.88 3.02 7 [4.34, 2.98] 12.92 22.54% 13.42 16.63% 4.06 3.00 8 [4.59, 2.98] 13.69 29.83% 13.24 17.80% 4.54 3.28 9 [4.87, 2.92] 14.21 34.77% 13.04 19.01% 4.67 3.20 表 2 数值算例2的部分优化解
序号 设计点 f1 增加 f2 减少 β1 β2 1 [1.01, 0.71, 1.64] 3.36 - 44.12 - 3.05 3.74 2 [1.02, 0.86, 1.68] 3.56 6.10% 36.40 17.49% 3.28 3.92 3 [1.04, 1.00, 1.74] 3.78 12.41% 30.64 30.56% 3.27 3.86 4 [1.03, 1.03, 1.75] 3.80 13.22% 29.62 32.87% 3.08 3.66 5 [1.01, 1.14, 1.89] 4.04 20.39% 26.10 40.85% 4.48 5.03 6 [1.05, 1.23, 1.87] 4.15 23.55% 24.22 45.10% 3.18 3.71 7 [1.06, 1.38, 1.99] 4.43 31.82% 21.22 51.90% 3.27 3.76 8 [1.29, 1.44, 1.95] 4.68 39.33% 20.72 53.04% 3.25 3.73 9 [1.40, 1.48, 1.95] 4.83 43.79% 20.31 53.98% 3.41 3.89 -
[1] Ni B Y, Jiang C, Huang Z L. Discussions on non-probabilistic convex modelling for uncertain problems[J]. Applied Mathematical Modelling, 2018, 59:54-85 doi: 10.1016/j.apm.2018.01.026 [2] Ben-Haim Y. Convex models of uncertainty in radial pulse buckling of shells[J]. Journal of Applied Mechanics, 1993, 60(3):683-688 doi: 10.1115/1.2900858 [3] 邱志平.非概率集合理论凸方法及其应用[M].北京:国防工业出版社, 2005Qiu Z P. Convex method based on non-probabilistic set-theory and its application[M]. Beijing:National Defense Industry Press, 2005(in Chinese) [4] Jiang C, Han X, Lu G Y, et al. Correlation analysis of non-probabilistic convex model and corresponding structural reliability technique[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(33-36):2528-2546 doi: 10.1016/j.cma.2011.04.007 [5] Kang Z, Zhang W B. Construction and application of an ellipsoidal convex model using a semi-definite programming formulation from measured data[J]. Computer Methods in Applied Mechanics and Engineering, 2016, 300:461-489 doi: 10.1016/j.cma.2015.11.025 [6] Elishakoff I, Elettro F. Interval, ellipsoidal, and super-ellipsoidal calculi for experimental and theoretical treatment of uncertainty:which one ought to be preferred?[J]. International Journal of Solids and Structures, 2014, 51(7-8):1576-1586 doi: 10.1016/j.ijsolstr.2014.01.010 [7] Jiang C, Bi R G, Lu G Y, et al. Structural reliability analysis using non-probabilistic convex model[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 254:83-98 doi: 10.1016/j.cma.2012.10.020 [8] Zhou Y T, Jiang C, Han X. Interval and subinterval analysis methods of the structural analysis and their error estimations[J]. International Journal of Computational Methods, 2006, 3(2):229-244 doi: 10.1142/S0219876206000771 [9] Liu J, Liu H, Jiang C, et al. A new measurement for structural uncertainty propagation based on pseudo-probability distribution[J]. Applied Mathematical Modelling, 2018, 63:744-760 doi: 10.1016/j.apm.2018.07.017 [10] Lombardi M. Optimization of uncertain structures using non-probabilistic models[J]. Computers & Structures, 1998, 67(1-3):99-103 http://d.old.wanfangdata.com.cn/Conference/8534829 [11] Wang M R, Fan J P, Hu J. A non-probabilistic reliability-based design optimization method for structures based on interval models[J]. Fatigue & Fracture of Engineering Materials & Structures, 2018, 41(2):425-439 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ee6381dc6080f2a31adef28d2545a3a5 [12] Guo S X, Lu Z Z. A non-probabilistic robust reliability method for analysis and design optimization of structures with uncertain-but-bounded parameters[J]. Applied Mathematical Modelling, 2015, 39(7):1985-2002 doi: 10.1016/j.apm.2014.10.026 [13] Hao P, Wang Y T, Liu C, et al. A novel non-probabilistic reliability-based design optimization algorithm using enhanced chaos control method[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 318:572-593 doi: 10.1016/j.cma.2017.01.037 [14] Hao P, Wang Y T, Liu X X, et al. An efficient adaptive-loop method for non-probabilistic reliability-based design optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 324:689-711 doi: 10.1016/j.cma.2017.07.002 [15] Zheng J, Luo Z, Jiang C, et al. Non-probabilistic reliability-based topology optimization with multidimensional parallelepiped convex model[J]. Structural and Multidisciplinary Optimization, 2018, 57(6):2205-2221 doi: 10.1007/s00158-017-1851-9 [16] Du X P, Chen W. Towards a better understanding of modeling feasibility robustness in engineering design[J]. Journal of Mechanical Design, 2000, 122(4):385-394 https://www.sciencedirect.com/science/article/pii/S0360835214001582 [17] Tang Y F, Chen J Q, Wei J H. A sequential algorithm for reliability-based robust design optimization under epistemic uncertainty[J]. Journal of Mechanical Design, 2012, 134(1):014502 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a3659b263160ce4e058318e05a51ee8e [18] Zhuang X T, Pan R, Du X P. Enhancing product robustness in reliability-based design optimization[J]. Reliability Engineering & System Safety, 2015, 138:145-153 https://www.sciencedirect.com/science/article/pii/S0951832015000368 [19] Wu J L, Gao J, Luo Z, et al. Robust topology optimization for structures under interval uncertainty[J]. Advances in Engineering Software, 2016, 99:36-48 doi: 10.1016/j.advengsoft.2016.05.002 [20] Cheng S, Zhou J H, Li M. A new hybrid algorithm for multi-objective robust optimization with interval uncertainty[J]. Journal of Mechanical Design, 2015, 137(2):021401 [21] 刘桂萍.基于微型遗传算法的多目标优化方法及应用研究[D].长沙: 湖南大学, 2008 http://cdmd.cnki.com.cn/Article/CDMD-10532-2008081553.htmLiu G P. Multi-objective optimization methods based on micro genetic algorithm and its application[D]. Changsha: Hunan University, 2008(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10532-2008081553.htm [22] Du X P, Chen W. Sequential optimization and reliability assessment method for efficient probabilistic design[J]. Journal of Mechanical Design, 2004, 126(2):225-233 https://asmedigitalcollection.asme.org/IDETC-CIE/proceedings/IDETC-CIE2002/36223/871/297709 [23] Huang Z L, Jiang C, Zhou Y S, et al. An incremental shifting vector approach for reliability-based design optimization[J]. Structural and Multidisciplinary Optimization, 2016, 53(3):523-543 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a6055205a2d81d1a830d18b31d7b6531 [24] Lee J O, Yang Y S, Ruy W S. A comparative study on reliability-index and target-performance-based probabilistic structural design optimization[J]. Computers & Structures, 2002, 80(3-4):257-269 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=CFKO200011921283243 -







 下载:
下载: