Zernike Polynomial Local Fitting Algorithm for Slow Tool Servo Machining
-
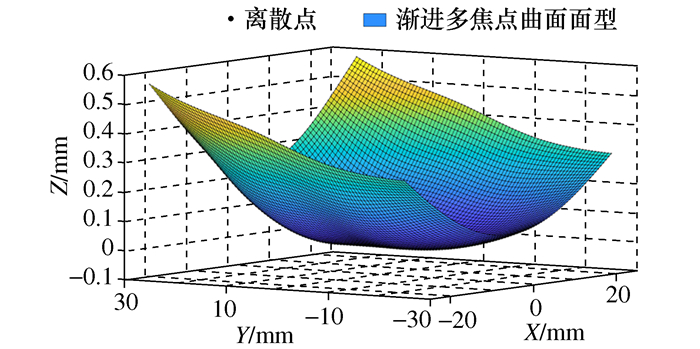
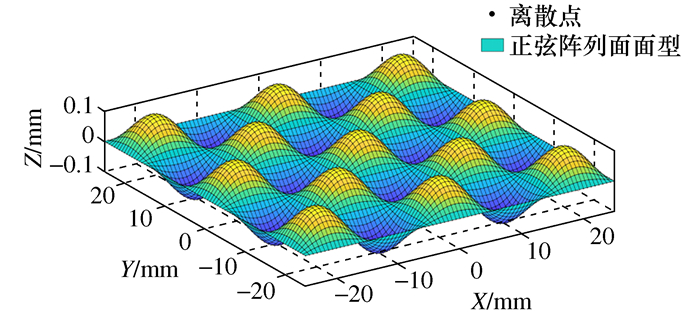
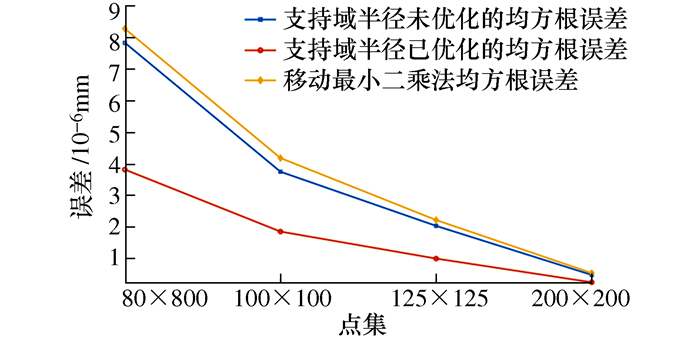
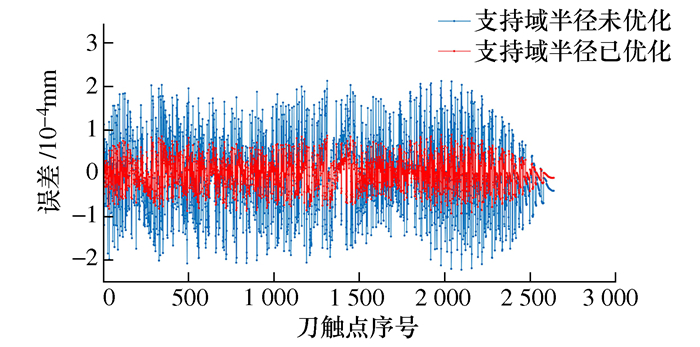
摘要: 针对慢刀伺服加工前后的曲面拟合问题,将Zernike多项式与移动最小二乘法结合,提出Zernike多项式局部拟合算法。使用Gram-Schmidt正交化构造正交基底函数,解决了拟合计算中出现的病态矩阵及矩阵求逆运算量大等问题。局部拟合中支持域半径对拟合精度影响显著,基于此提出了支持域半径优化算法。以渐进多焦点曲面、环曲面、正弦阵列面为例,采用与慢刀伺服加工关系密切的刀触点精度及拟合优度R-square作为评价标准,在MATLAB软件中进行了数值仿真。结果表明,Zernike多项式局部拟合算法各项标准均优于移动最小二乘法,并且算法在经过半径优化后,不仅进一步提高了精度、改善了拟合优度,还改善了刀触点误差的离散程度。
-
关键词:
- 慢刀伺服 /
- Zernike多项式 /
- 局部拟合 /
- 正交基底函数 /
- 支持域半径 /
Abstract: In order to solve the surface fitting problem before and after slow tool servo machining, this paper combines Zernike polynomial with moving least squares and proposes Zernike polynomial local fitting algorithm. In this paper, the Gram-Schmidt orthogonalization algorithm is used to construct the orthogonal basis function. This method solves the problems of the ill-conditioned matrix problem and the large amount of matrix inversion in the calculation process of the fitting algorithm. The support domain radius in the local fitting has a significant influence on the fitting accuracy. Based on this, the support domain radius optimization algorithm is proposed. Taking progressive-addition lenses, toric surface and sinusoidal array surface as examples, the accuracy of the cutting location points and the goodness of fit R-square, which are closely related to the slow tool servo machining, are used as the evaluation criteria. Numerical simulation is carried out in MATLAB software, the results show that the Zernike polynomial local fitting algorithm is better than the moving least squares method, and after the support domain radius optimization, the algorithm not only further improves the accuracy and the goodness of fit, but also improves the discrete degree on the cutting location points error. -
表 1 Zernike多项式前6项表达式
1 1 1 2 2ρsinθ 2x 3 2ρcosθ 2y 4 

5 
2 
6 

表 2 渐进多焦点曲面刀触点均方根误差计算结果
点集 误差/mm 移动最小
二乘法半径未优化
Zernike法半径已优化
Zernike法50×50 3.262 6×10-5 3.083 4×10-5 1.463 8×10-5 80×80 8.283 4×10-6 7.837 0×10-6 3.822 9×10-6 100×100 4.187 6×10-6 3.754 5×10-6 1.860 1×10-6 125×125 2.225 4×10-6 2.040 5×10-6 1.005 9×10-6 200×200 5.476 5×10-7 4.883 7×10-7 2.550 2×10-7 表 3 环曲面刀触点均方根误差计算结果
点集 误差/mm 移动最小
二乘法半径未优化
Zernike法半径已优化
Zernike法50×50 5.086 7×10-6 3.208 0×10-6 2.473 6×10-6 80×80 1.180 3×10-6 7.448 0×10-7 6.071 2×10-7 100×100 6.184 4×10-7 3.991 7×10-7 3.088 0×10-7 125×125 3.089 4×10-7 1.997 4×10-7 1.590 3×10-7 200×200 7.425 3×10-8 4.726 2×10-8 3.768 2×10-8 表 4 正弦阵列面刀触点均方根误差计算结果
点集 误差/mm 移动最小
二乘法半径未优化
Zernike法半径已优化
Zernike法50×50 7.300 6×10-4 7.116 2×10-4 2.849 3×10-4 80×80 1.859 1×10-4 1.754 8×10-4 7.033 6×10-5 100×100 9.431 7×10-5 9.008 1×10-5 3.608 1×10-5 125×125 4.853 6×10-5 4.597 2×10-5 1.840 4×10-5 200×200 1.260 3×10-5 1.177 9×10-5 4.710 0×10-6 表 5 渐进多焦点曲面刀触点误差标准差计算结果
点集 误差/mm 移动最小
二乘法半径未优化
Zernike法半径已优化
Zernike法50×50 3.200 6×10-5 3.076 2×10-5 1.462 4×10-5 80×80 8.194 8×10-6 7.836 8×10-6 3.822 4×10-6 100×100 4.134 7×10-6 3.753 5×10-6 1.860 0×10-6 125×125 2.197 4×10-6 2.039 4×10-6 1.005 8×10-6 200×200 5.434 6×10-7 4.883 6×10-7 2.550 1×10-7 表 6 环曲面刀触点误差标准差计算结果
点集 误差/mm 移动最小
二乘法半径未优化
Zernike法半径已优化
Zernike法50×50 4.962 6×10-6 3.168 6×10-6 2.468 8×10-6 80×80 1.034 6×10-6 7.395 7×10-7 6.067 9×10-7 100×100 5.435 6×10-7 3.979 5×10-7 3.085 1×10-7 125×125 2.708 3×10-7 1.992 6×10-7 1.589 9×10-7 200×200 6.458 4×10-8 4.721 9×10-8 3.765 1×10-8 表 7 正弦阵列面刀触点误差标准差计算结果
点集 误差/mm 移动最小
二乘法半径未优化
Zernike法半径已优化
Zernike法50×50 7.296 7×10-4 7.085 5×10-4 2.843 6×10-4 80×80 1.859 1×10-4 1.752 9×10-4 7.030 9×10-5 100×100 9.431 5×10-5 8.999 7×10-5 3.606 6×10-5 125×125 4.835 4×10-5 4.592 5×10-5 1.839 5×10-5 200×200 1.259 4×10-5 1.177 9×10-5 4.709 9×10-6 表 8 正弦阵列面R-square结果对比
算法
点集移动最小
二乘法半径未优化
Zernike法半径已优化
Zernike法50×50 0.997 9 0.998 0 0.999 5 80×80 0.999 7 0.999 8 0.999 9 100×100 0.999 9 0.999 9 1.000 0 125×125 0.999 9 1.000 0 1.000 0 200×200 1.000 0 1.000 0 1.000 0 -
[1] 王兴盛, 康敏.基于Hermite插值的复杂光学曲面车削加工路径规划[J].机械工程学报, 2012, 48(11):191-198 http://d.old.wanfangdata.com.cn/Periodical/jxgcxb201211023Wang X S, Kang M. Cutting path planning for complex optical surface using Hermite interpolation[J]. Journal of Mechanical Engineering, 2012, 48(11):191-198(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jxgcxb201211023 [2] 何雪明, 孔丽娟, 何俊飞.基于自适应测量和实时重构的自由曲面特征产品的逆向研究[J].机械科学与技术, 2015, 34(1):99-102 doi: 10.13433/j.cnki.1003-8728.2015.0121He X M, Kong L J, He J F. Study on the reverse free-form feature of products based on the self-adaptive measurement and real-time reconstruction[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(1):99-102(in Chinese) doi: 10.13433/j.cnki.1003-8728.2015.0121 [3] 石广丰, 史国权, 徐军龙, 等.慢刀伺服车削渐进多焦点透镜的刀具路径生成与实验[J].制造业自动化, 2017, 39(7):46-47, 53 doi: 10.3969/j.issn.1009-0134.2017.07.012Shi G F, Shi G Q, Xu J L, et al. Tool path generation and experiment of progressive addition lens based on slow tool servo turning[J]. Manufacturing Automation, 2017, 39(7):46-47, 53(in Chinese) doi: 10.3969/j.issn.1009-0134.2017.07.012 [4] 王兴盛.复杂光学曲面慢刀伺服车削关键技术研究[D].南京: 南京农业大学, 2014 http://d.g.wanfangdata.com.cn/Thesis_Y2974386.aspxWang X S. Research on the key technologies of slow tool servo turning for complex optical surface[D]. Nanjing: Nanjing Agriculture University, 2014(in Chinese) http://d.g.wanfangdata.com.cn/Thesis_Y2974386.aspx [5] 李晶.光学曲面表面形貌的重构与评价[D].长春: 长春工业大学, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10190-1016759704.htmLi J. Reconstruction and evaluation of surface topography of optical surface[D]. Changchun: Changchun University of Technology, 2016(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10190-1016759704.htm [6] 钟锡健, 张更新, 谢智东.基于移动最小二乘法的天线增益模型构建[J].通信技术, 2016, 49(5):549-553 doi: 10.3969/j.issn.1002-0802.2016.05.008Zhong X J, Zhang G X, Xie Z D. Construction of antenna gain model based on movable least square[J]. Communications Technology, 2016, 49(5):549-553(in Chinese) doi: 10.3969/j.issn.1002-0802.2016.05.008 [7] 关朝亮, 王建敏, 戴一帆, 等.基于Zernike多项式拟合的自由曲面车削误差补偿技术[J].国防科技大学学报, 2010, 32(2):135-140 doi: 10.3969/j.issn.1001-2486.2010.02.025Guan C L, Wang J M, Dai Y F, et al. Figure error compensation of freeform surface turning based on Zernike polynomial fitting[J]. Journal of National University of Defense Technology, 2010, 32(2):135-140(in Chinese) doi: 10.3969/j.issn.1001-2486.2010.02.025 [8] 李广年.复杂曲面拟合与误差分析研究[D].长春: 吉林大学, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10183-1016083517.htmLi G N. Research on curved surface fitting and error analysis[D]. Changchun: Jilin University, 2016(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10183-1016083517.htm [9] 陈旭.慢刀伺服车削机床PID参数优化及其刀具路径规划研究[D].南京: 南京农业大学, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10307-1017261568.htmChen X. Research on PID parameter optimization and tool path generation of slow tool servo turning machine[D]. Nanjing: Nanjing Agriculture University, 2016(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10307-1017261568.htm [10] 牛恒泰, 康敏, 何成奎, 等.离散曲面慢刀伺服车削刀具路径规划[J].机械科学与技术, 2018, 37(5):721-728 doi: 10.13433/j.cnki.1003-8728.2018.0511Niu H T, Kang M, He C K, et al. Cutting path plan of discrete surface for slow tool servo turning[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(5):721-728(in Chinese) doi: 10.13433/j.cnki.1003-8728.2018.0511 [11] 汤先鹏, 李柏渝, 陈雷, 等.利用曲线拟合改善压控衰减器精度的方法[J].全球定位系统, 2016, 41(4):12-16 http://d.old.wanfangdata.com.cn/Periodical/qqdwxt201604003Tang X P, Li B Y, Chen L, et al. The method of applying the curve fitting to improve the accuracy of voltage variable attenuators[J]. GNSS World of China, 2016, 41(4):12-16(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/qqdwxt201604003 [12] 于成龙, 刘莉, 龙腾, 等.基于优化的改进移动最小二乘代理模型方法[J].航空计算技术, 2013, 43(1):85-88 doi: 10.3969/j.issn.1671-654X.2013.01.022Yu C L, Liu L, Long T, et al. An improved moving least square method metamodal based on optimization[J]. Aeronautical Computing Technique, 2013, 43(1):85-88(in Chinese) doi: 10.3969/j.issn.1671-654X.2013.01.022 [13] Liu G R. Mesh free methods:moving beyond the finite element method[J]. Applied Mechanics Reviews, 2003, 56(2):B17-B18 https://www.routledge.com/Meshfree-Methods-Moving-Beyond-the-Finite-Element-Method-Second-Edition/Liu/p/book/9781138372702 [14] 左传伟, 聂玉峰, 赵美玲.移动最小二乘方法中影响半径的选取[J].工程数学学报, 2005, 22(5):833-838 doi: 10.3969/j.issn.1005-3085.2005.05.011Zuo C W, Nie Y F, Zhao M L. The selection about the radius of influence in MLS[J]. Chinese Journal of Engineering Mathematics, 2005, 22(5):833-838(in Chinese) doi: 10.3969/j.issn.1005-3085.2005.05.011 [15] 关朝亮, 铁贵鹏, 尹自强.光学阵列器件的慢刀伺服车削加工技术[J].国防科技大学学报, 2009, 31(4):31-35, 47 doi: 10.3969/j.issn.1001-2486.2009.04.007Guan C L, Tie G P, Yin Z Q. Fabrication of array lens optical component by using of slow tool servo diamond turning[J]. Journal of National University of Defense Technology, 2009, 31(4):31-35, 47(in Chinese) doi: 10.3969/j.issn.1001-2486.2009.04.007 -







 下载:
下载: