Applying Improved CMA-ES Algorithm to Solve Inverse Kinematics of 7-DOF Humanoid Arm
-
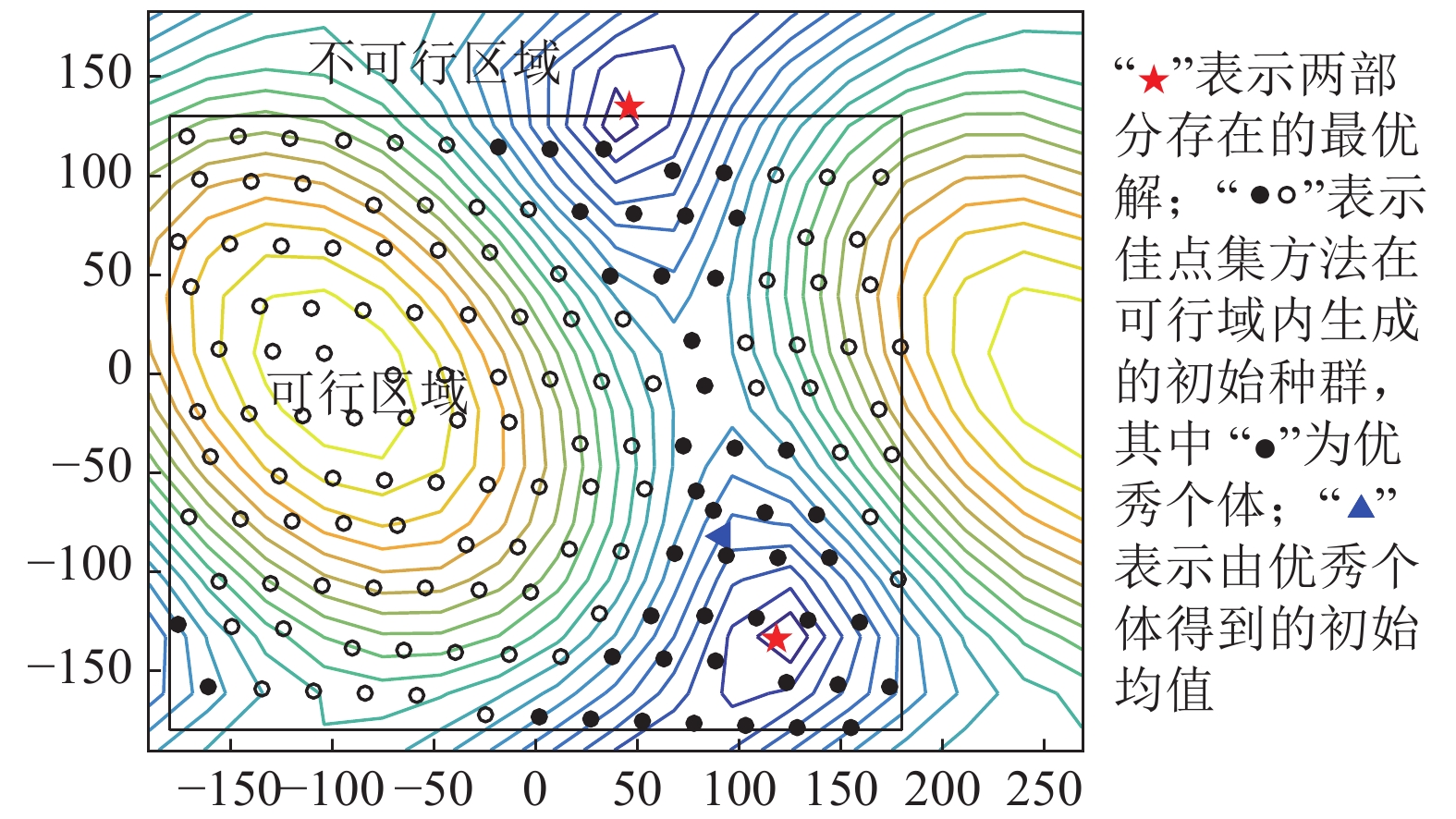
摘要: 提出一种改进的CMA-ES算法:将原算法随机生成初始均值点,改为由佳点集中优秀个体加权求和得到;增加越界敏感因子和步长缩放系数,用于新个体存在越界行为时,修正步长更新。以7自由度仿人臂为例,用改进的CMA-ES算法求逆运动学解,结果表明改进的CMA-ES算法可实时、高精度地求解:在点对点运动中,改进的算法单次求解时间约为9.7 ms,适应度函数稳定在10−8级别;在工作空间的连续轨迹中,位置跟踪误差稳定在10−5 mm级别,单次平均求解时间约为14.1 ms。Abstract: This paper proposes an improved CMA-ES algorithm. Firstly, the original algorithm randomly generates the initial mean point, which is modified to the weighted sum of excellent individuals in good point sets. Then, the cross-border sensitivity factor and step-size scaling factor are added to adjust step size updates, when the new individuals have cross-border behaviour. Taking the 7-DOF humanoid arm as an example, the inverse kinematic solution is obtained with the improved CMA-ES algorithm. The simulation results show that the improved CMA-ES algorithm can solve the inverse kinematics of 7-DOF humanoid arm in real-time and with high-precision. In point-to-point motion, the single solution time is about 9.7 ms, and the fitness function is stable at the 10−8 level. In the continuous trajectory of workspace, the position tracking error is stable at the 10−5 mm level, and the single average solution time is about 14.1 ms.
-
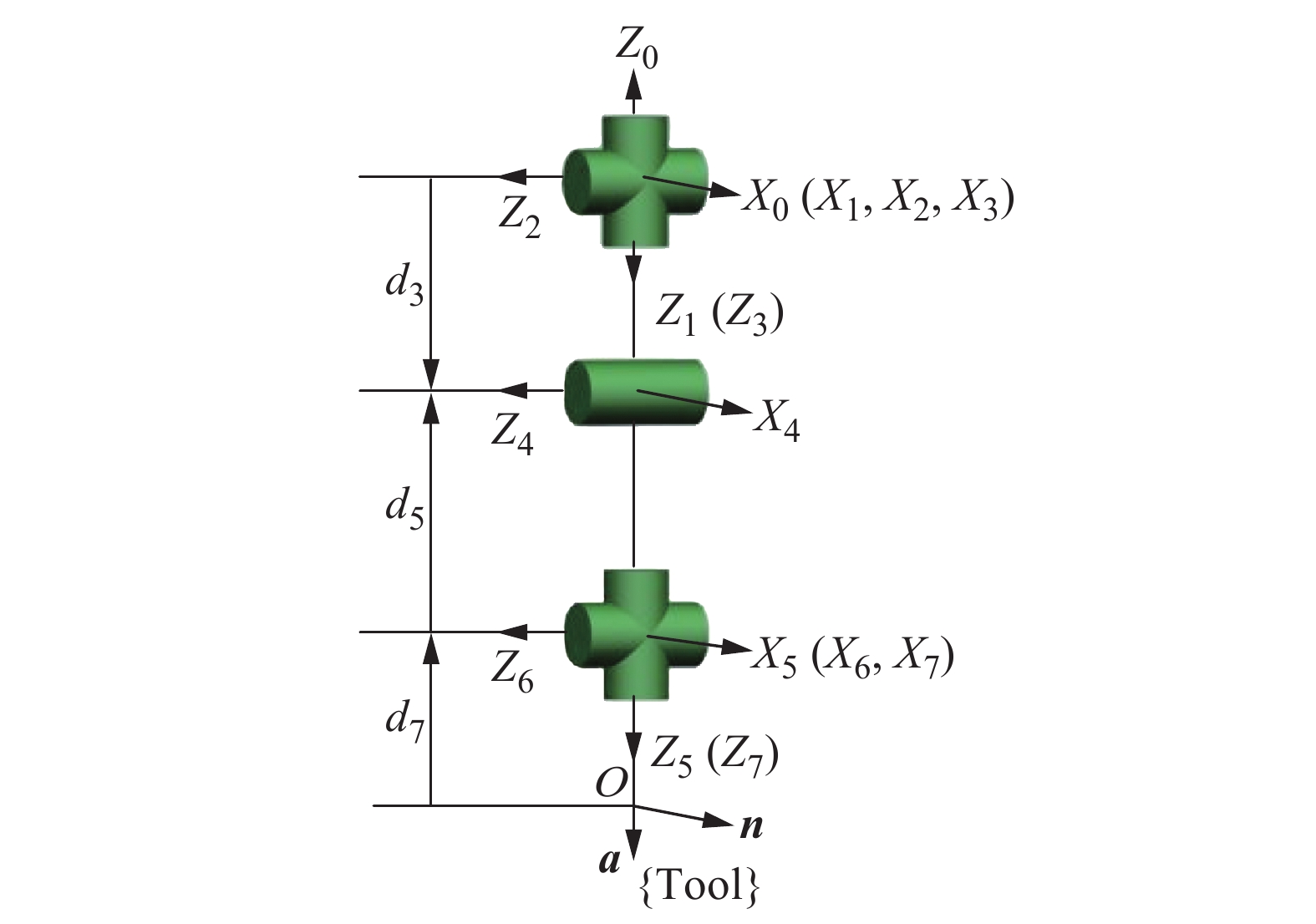
表 1 拟人臂的连杆参数
连杆i 关节角θi/(°) 扭角αi−1/(°) 长度ai−1/mm 偏置di/mm 1 θ1 180 0 0 2 θ2 −90 0 0 3 θ3 90 0 d3 4 θ4 −90 0 0 5 θ5 90 0 d5 6 θ6 −90 0 0 7 θ7 90 0 0 表 2 关节角取值范围
(°) 关节 θ1 θ2 θ3 θ4 θ5 θ6 θ7 上限 −170 −170 −170 0 −120 −120 −170 下限 170 170 170 180 120 120 170 表 3 3种算法独立运行1 000次的f1结果
f1 原CMA-ES 改进的CMA-ES 遗传算法 最小值 2.262 8×10−8 6.700 5×10−9 1.873 1×10−4 最大值 1.748 1×10−7 9.987 2×10−8 0.021 7 平均值 7.648 7×10−8 6.939 4×10−8 0.005 8 标准差 1.663 7×10−8 1.842 0×10−8 0.003 6 平均求解时间/s 0.022 6 0.009 7 0.346 表 4 轨迹采样点的位置绝对误差
位置绝对误差 改进的CMA-ES 原CMA-ES 最小值/mm 2.089 6×10−6 2.316 4×10−6 最大值/mm 2.121 9×10−5 2.128 6×10−5 平均值/mm 1.092 7×10−5 1.172 3×10−5 标准差/mm 4.735 9×10−6 4.975 6×10−6 平均求解时间/s 0.014 1 0.021 6 -
[1] 任子武, 王振华, 孙立宁. 全局和声搜索方法及其在仿人灵巧臂逆运动学求解中的应用[J]. 控制理论与应用, 2012, 29(7): 867-876Ren Z W, Wang Z H, Sun L N. A global harmony search algorithm and its application to inverse kinematics problem for humanoid arm[J]. Control Theory & Applications, 2012, 29(7): 867-876 (in Chinese) [2] 姜宏超, 刘士荣, 张波涛. 六自由度模块化机械臂的逆运动学分析[J]. 浙江大学学报, 2010, 44(7): 1348-1354 doi: 10.3785/j.issn.1008-973X.2010.07.021Jiang H C, Liu S R, Zhang B T. Inverse kinematics analysis for 6 degree-of-freedom modular manipulator[J]. Journal of Zhejiang University, 2010, 44(7): 1348-1354 (in Chinese) doi: 10.3785/j.issn.1008-973X.2010.07.021 [3] 王英石, 孙雷, 刘景泰. 基于空间几何方法的乒乓球机器人最优姿态求取[J]. 机器人, 2014, 36(2): 203-209Wang Y S, Sun L, Liu J T. Optimal pose solution based on space geometry method for Pingpong robot[J]. Robot, 2014, 36(2): 203-209 (in Chinese) [4] 房立金, 高瑞. 一般6R机器人逆运动学算法的改进[J]. 机械科学与技术, 2018, 37(9): 1325-1330Fang L J, Gao R. Improving inverse kinematics algorithm for general 6-DOF robots[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(9): 1325-1330 (in Chinese) [5] Pieper D L. The kinematics of manipulators under computer control[D]. Palo Alto, California: Stanford University, 1968 [6] Duffy J. Analysis of mechanisms and robot manipulators[M]. London: Edward Arnold, 1980: 369-409 [7] 王俊龙, 张国良, 敬斌, 等. 一种新的六自由度机械臂运动学反解方法研究[J]. 计算机工程与应用, 2013, 49(22): 266-270 doi: 10.3778/j.issn.1002-8331.1202-0308Wang J L, Zhang G L, Jing B, et al. Research on way of inverse kinematic solution of six DOF manipulator[J]. Computer Engineering and Applications, 2013, 49(22): 266-270 (in Chinese) doi: 10.3778/j.issn.1002-8331.1202-0308 [8] 林阳, 赵欢, 丁汉. 基于多种群遗传算法的一般机器人逆运动学求解[J]. 机械工程学报, 2017, 53(3): 1-8 doi: 10.3901/JME.2017.03.001Lin Y, Zhao H, Ding H. Solution of inverse kinematics for general robot manipulators based on multiple population genetic algorithm[J]. Journal of Mechanical Engineering, 2017, 53(3): 1-8 (in Chinese) doi: 10.3901/JME.2017.03.001 [9] 周枫林, 游雨龙, 李光. 空间3R机械臂逆向运动学的奇异轨迹线方法研究[J]. 机械科学与技术, 2019, 38(3): 365-372Zhou F L, You Y L, Li G. A solving method for inverse kinematics of space 3R manipulator based on singular trajectory theory[J]. Mechanical Science and Technology for Aerospace Engineering, 2019, 38(3): 365-372 (in Chinese) [10] 张熙峰, 田景文. 基于遗传算法的机械臂逆运动学问题解决方案[J]. 计算机工程与应用, 2017, 53(22): 150-156 doi: 10.3778/j.issn.1002-8331.1607-0007Zhang X F, Tian J W. Solution based on genetic algorithm for inverse problem of manipulator kinematics[J]. Computer Engineering and Applications, 2017, 53(22): 150-156 (in Chinese) doi: 10.3778/j.issn.1002-8331.1607-0007 [11] Auger A, Hansen N. A restart CMA evolution strategy with increasing population size[C]// Proceedings of 2005 IEEE Congress on Evolutionary Computation. Edinburgh, Scotland, UK: IEEE, 2005: 1769-1776 [12] Hansen N. The CMA evolution strategy: a comparing review[M]//Lozano J A, Larrañaga P, Inza I, et al. Towards a New Evolutionary Computation. Berlin, Heidelberg: Springer, 2006: 75-102 [13] Alrashdi Z, Sayyafzadeh M. (μ+λ) Evolution strategy algorithm in well placement, trajectory, control and joint optimisation[J]. Journal of Petroleum Science and Engineering, 2019, 177: 1042-1058 doi: 10.1016/j.petrol.2019.02.047 [14] Chen L, Zheng Z, Liu H L, et al. An evolutionary algorithm based on covariance matrix leaning and searching preference for solving CEC 2014 benchmark problems[C]//Proceedings of 2014 IEEE Congress on Evolutionary Computation (CEC). Beijing: IEEE, 2014: 2672-2677 [15] Ghosh S, Das S, Roy S, et al. A differential covariance matrix adaptation evolutionary algorithm for real parameter optimization[J]. Information Sciences, 2012, 182(1): 199-219 doi: 10.1016/j.ins.2011.08.014 [16] Preuss M. Niching the CMA-ES via nearest-better clustering[C]//Proceedings of the 12th Annual Conference Companion on Genetic and Evolutionary Computation. Portland, OR, USA: ACM, 2010: 1711-1718 [17] Li L X, Tang K. History-based topological speciation for multimodal optimization[J]. IEEE Transactions on Evolutionary Computation, 2015, 19(1): 136-150 doi: 10.1109/TEVC.2014.2306677 [18] Igel C, Hansen N, Roth S. Covariance matrix adaptation for multi-objective optimization[J]. Evolutionary Computation, 2007, 15(1): 1-28 doi: 10.1162/evco.2007.15.1.1 [19] Loshchilov I. A computationally efficient limited memory CMA-ES for large scale optimization[C]// Proceedings of 2014 Annual Conference on Genetic and Evolutionary Computation. Vancouver, BC, Canada: ACM, 2014: 397-404 [20] 刘金鹏. 面向大规模实值优化问题的CMA-ES算法及其分制策略研究[D]. 合肥: 中国科学技术大学, 2014Liu J P. CMA-ES and decomposition strategy for large scale continuous optimization problem[D]. Hefei: University of Science and Technology of China, 2014 (in Chinese) [21] 程沙沙. 结构动力优化设计的进化策略方法[D]. 南宁: 广西大学, 2012Cheng S S. Evolution strategy method for structural dynamic optimization[D]. Nanning: Guangxi University, 2012 (in Chinese) [22] Fujii G, Akimoto Y, Takahashi M. Exploring optimal topology of thermal cloaks by CMA-ES[J]. Applied Physics Letters, 2018, 112(6): 061108 doi: 10.1063/1.5016090 [23] 黄亚飞, 梁昔明, 陈义雄. 求解全局优化问题的正交协方差矩阵自适应进化策略算法[J]. 计算机应用, 2012, 32(4): 981-985Huang Y F, Liang X M, Chen Y X. Hybrid orthogonal CMAES for solving global optimization problems[J]. Journal of Computer Applications, 2012, 32(4): 981-985 (in Chinese) [24] 陈海兵. 基于CMA-ES算法的太赫兹人工电磁材料设计[D]. 南京: 东南大学, 2016Chen H B. Design of terahertz metamateria based on the covariance matrix adaptation evolutionary strategy[D]. Nanjing: Southeast University, 2016 (in Chinese) [25] 孙家泽, 王刚. 利用佳点集遗传算法的白盒测试用例优先排序[J]. 计算机工程与科学, 2018, 40(10): 1815-1821 doi: 10.3969/j.issn.1007-130X.2018.10.013Sun J Z, Wang G. White box test case prioritization based on good point set genetic algorithm[J]. Computer Engineering & Science, 2018, 40(10): 1815-1821 (in Chinese) doi: 10.3969/j.issn.1007-130X.2018.10.013 [26] 肖赤心. 高维优化进化算法及其应用研究[D]. 长沙: 中南大学, 2009Xiao C X. Research on evolutionary algorithms for high dimensional optimization and their applications[D]. Changsha: Central South University, 2009 (in Chinese) [27] Corke P. 机器人学、机器视觉与控制——MTALAB算法基础[M]. 刘荣, 译. 北京: 电子工业出版社, 2016: 156-157Corker P. Robotics, vision and control: fundamental algorithm in MATLAB[M]. Liu R, trans. Beijing: Publishing House of Electronics Industry, 2016: 156-157 (in Chinese) [28] 蔡自兴, 谢斌. 机器人学[M]. 3版. 北京: 清华大学出版社, 2015: 19-26Cai Z X, Xie B. Robotics[M]. 3rd ed. Beijing: Tsinghua University Press, 2015: 19-26 (in Chinese) -








 下载:
下载: