Path Smoothing Algorithm of Mobile Robot based on DP-B Spline
-
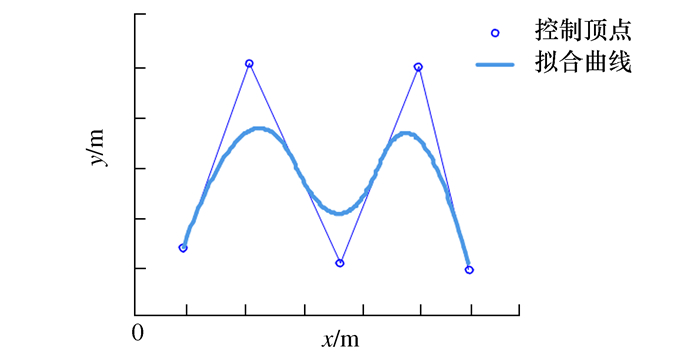
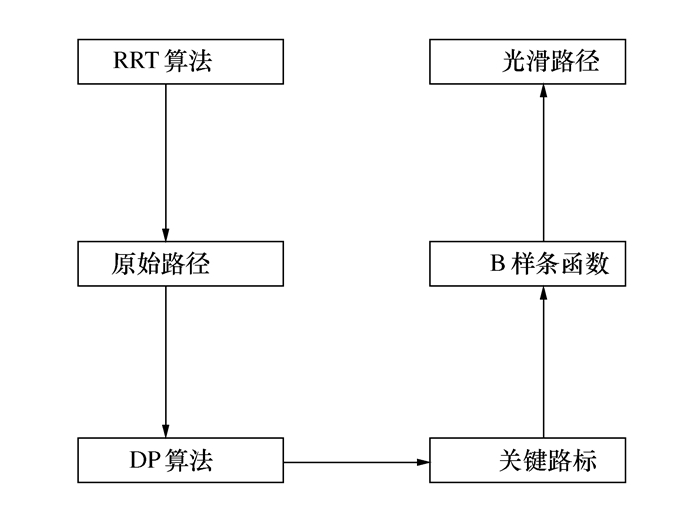
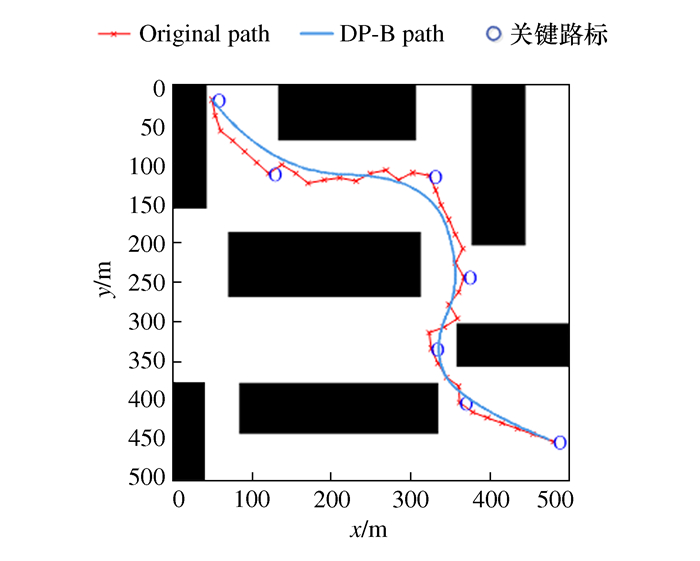
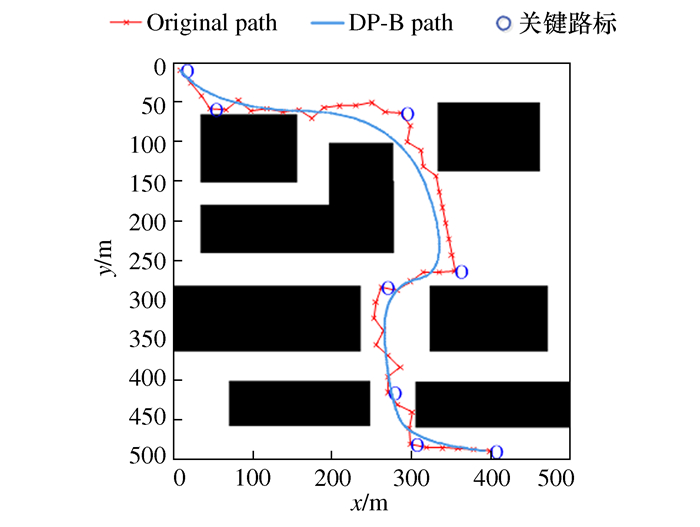
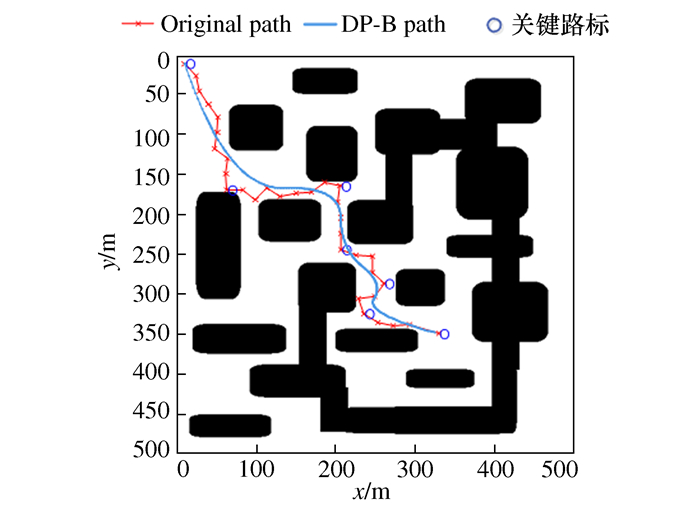
摘要: 针对快速扩展随机树算法(RRT)产生的路径冗余点过多与路径转折点较多的问题,提出了一种基于Douglas-Peucker算法及B样条函数的路径光滑算法。首先,利用Douglas-Peucker(DP)算法从RRT算法产生的路径节点中提取出若干节点作为关键路标;然后,采用B样条函数拟合关键路标,得到一条曲率连续的光滑路径,实现规划路径的光滑化。通过在不同环境中进行实验和与其他路径光滑算法实验进行对比,结果表明,该算法能够明显缩短优化路径的路径长度,明显减少优化路径转折次数,大幅度提升优化路径的光滑度,有利于减少机器人在单次航程中的能量消耗,完成更多任务,有效提升机器人的工作效率。Abstract: Aiming at the problem of too many redundant points and more turning points of paths generated by the Rapidly-exploring Random Tree algorithm (RRT), this paper proposes a path smoothing algorithm based on Douglas-Peucker algorithm and B-spline function to solve it. Firstly, the Douglas-Peucker (DP) algorithm is used to extract several nodes from the path nodes which generated by the RRT algorithm as key road signs. Then, in order to achieve a smooth planning path, the B-spline function is used to fit the key road signs to obtain a smooth path with continuous curvature. By experimenting in different environments and comparing the tests obtained by other path smoothing algorithms, the results show that the algorithm can significantly cut down the path length and reduce the transition number of optimized path, and it also greatly improve the smoothness of the optimized path. It is beneficial to reduce the energy consumption of the robot in a single voyage and make it complete more tasks, which can improve the robot's working efficiency effectively.
-
Key words:
- robot /
- path smoothing /
- RRT /
- Douglas-Peucker algorithm (DP) /
- key road signs /
- B-spline function /
- path optimization
-
表 1 传统RRT算法及DP-B算法性能测试对比结果
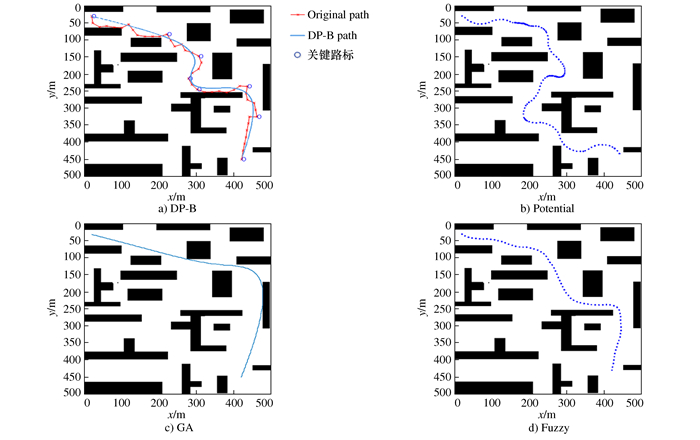
表 2 四种算法性能测试对比结果
算法 路径长度/m 转折次数 时间/s DP-B 757.27 3 3.06 Potential 912.92 12 4.67 GA 844.03 1 14.94 Fuzzy 808.25 3 5.98 -
[1] Tsardoulias E G, Iliakopoulou A, Kargakos A, et al. A review of global path planning methods for occupancy grid maps regardless of obstacle density[J]. Journal of Intelligent & Robotic Systems, 2016, 84(1-4):829-858 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=642e8057c9701f5f593cc79b471f73f8 [2] Lv T Z, Feng M Y. A smooth local path planning algorithm based on modified visibility graph[J]. Modern Physics Letters B, 2017, 31(19-21):1740091 doi: 10.1142/S0217984917400917 [3] Lv T Z, Zhao C X, Xia P P. Global path planning based on simultaneous visibility graph construction and A* algorithm[J]. Journal of Nanjing University of Science and Technology, 2017, 41(3):313-321 doi: 10.14177/j.cnki.32-1397n.2017.41.03.007 [4] Candeloro M, Lekkas A M, Sørensen A J, et al. Continuous curvature path planning using voronoi diagrams and fermat's spirals[J]. IFAC Proceedings Volumes, 2013, 46(33):132-137 doi: 10.3182/20130918-4-JP-3022.00064 [5] Broutin N, Devillers O, Hemsley R. Efficiently navigating a random delaunay triangulation[J]. Random Structures & Algorithms, 2016, 49(1):95-136 http://cn.bing.com/academic/profile?id=0a61e027fa87fe6a48c386c12ff77673&encoded=0&v=paper_preview&mkt=zh-cn [6] Liu J H, Yang J G, Liu H P, et al. An improved ant colony algorithm for robot path planning[J]. Soft Computing, 2017, 21(19):5829-5839 doi: 10.1007/s00500-016-2161-7 [7] 徐林, 范昕炜.基于改进遗传算法的餐厅服务机器人路径规划[J].计算机应用, 2017, 37(7):1967-1971 http://d.old.wanfangdata.com.cn/Periodical/jsjyy201707026Xu L, Fan X W. Path planning for restaurant service robot based on improved genetic algorithm[J]. Journal of Computer Applications, 2017, 37(7):1967-1971(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jsjyy201707026 [8] Elbanhawi M, Simic M. Sampling-based robot motion planning:a review[J]. IEEE Access, 2014, 2:56-77 doi: 10.1109/ACCESS.2014.2302442 [9] Kavraki L E, LaValle S M. Motion planning[M]//Siciliano B, Khatib O. Springer Handbook of Robotics. Cham: Springer, 2016: 139-162 [10] Kwangjin Y, Jung D, Sukkarieh S. Continuous curvature path-smoothing algorithm using cubic bézier spiral curves for non-holonomic robots[J]. Advanced Robotics, 2013, 27(4):247-258 doi: 10.1080/01691864.2013.755246 [11] Elbanhawi M, Simic M, Jazar R N. Continuous path smoothing for car-like robots using b-spline curves[J]. Journal of Intelligent & Robotic Systems, 2015, 80(1):23-56 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=79ce0a19689795e03dfc48c2e220ff9b [12] 张璐, 张国良, 张维平, 等.基于粒子群三次样条优化的局部路径规划方法[J].计算机技术与发展, 2012, 22(11):145-148 http://d.old.wanfangdata.com.cn/Periodical/wjfz201211039Zhang L, Zhang G L, Zhang W P, et al. Local path planning algorithm based on particle swarm optimization of cubic splines[J]. Computer Technology and Development, 2012, 22(11):145-148(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/wjfz201211039 [13] 陈呈, 王直.基于改进势场栅格法的全局路径规划与平光滑[J].信息通信, 2018(6):17-20, 23 doi: 10.3969/j.issn.1673-1131.2018.06.005Chen C, Wang Z. Global Path planning and smoothing based on improved potential field grid method[J]. Information & Communications, 2018(6):17-20, 23(in Chinese) doi: 10.3969/j.issn.1673-1131.2018.06.005 [14] LaValle S M. Rapidly-exploring random trees: A new tool for path planning[R]. Ames: Iowa State University, 1998 [15] Li Y, Cui R X, Li Z J, et al. Neural network approximation based near-optimal motion planning with kinodynamic constraints using RRT[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11):8718-8729 doi: 10.1109/TIE.2018.2816000 [16] Yin G Y, Zhou S L, Wu Q P. An improved RRT algorithm for UAV path planning[J]. Acta Electronica Sinica, 2017, 45(7):1764-1769 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dianzixb201707029 [17] Douglas D H, Peucker T K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J]. Cartographica:The International Journal for Geographic Information and Geovisualization, 1973, 10(2):112-122 doi: 10.3138/FM57-6770-U75U-7727 [18] Prasad D K, Leung M K H, Quek C, et al. A novel framework for making dominant point detection methods non-parametric[J]. Image and Vision Computing, 2012, 30(11):843-859 doi: 10.1016/j.imavis.2012.06.010 [19] Elbanhawi M, Simic M, Jazar R. Randomized bidirectional B-spline parameterization motion planning[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(2):406-419 doi: 10.1109/TITS.2015.2477355 [20] Uyar K, Vlker E. B-spline curve fitting with invasive weed optimization[J]. Applied Mathematical Modelling, 2017, 52:320-340 doi: 10.1016/j.apm.2017.07.047 [21] Francis B, Elliott A, Weldon M. Smoothing group-based trajectory models through B-splines[J]. Journal of Developmental and Life-Course Criminology, 2016, 2(1):113-133 doi: 10.1007/s40865-016-0025-6 [22] 曹凯, 周芦芦, 张政新.基于道路势场的智能车辆机动驾驶控制算法[J].系统仿真学报, 2011, 23(10):2206-2210 http://d.old.wanfangdata.com.cn/Conference/7646655Cao K, Zhou L L, Zhang Z X. Controlled algorithm for intelligent vehicle maneuver driving based on road potential field[J]. Journal of System Simulation, 2011, 23(10):2206-2210(in Chinese) http://d.old.wanfangdata.com.cn/Conference/7646655 [23] 王宪, 盛巍, 宋书林, 等.基于遗传算法和B样条曲线的平滑避障路径规划[J].计算机系统应用, 2012, 21(2):65-71 doi: 10.3969/j.issn.1003-3254.2012.02.016Wang X, Sheng W, Song S L, et al. Smoothing obstacle avoidance path planning based on genetic algorithms and B-spline curve[J]. Computer Systems & Applications, 2012, 21(2):65-71(in Chinese) doi: 10.3969/j.issn.1003-3254.2012.02.016 [24] Deng J Q, Hao C, Liu Y. Path planning research of soccer robot based on fuzzy theory[J]. Advanced Materials Research, 2012, 462:580-586 doi: 10.4028/www.scientific.net/AMR.462.580 -







 下载:
下载: