Optimizing Topological Design of Compliant Mechanism with Steady Change in its Configuration with Heaviside Density Projection
-
摘要: 现有柔性机构拓扑优化方法在解决柔性机构拓扑优化的类铰链和灰度问题仍存在一些困难。为获得清晰和不含类铰链的优化拓扑,提出了一种构型平稳变化的结构拓扑优化求解方法。首先,构建了一种能综合表征柔性机构输入和输出端的局部刚度特性的加权组合柔顺度函数;而后,引入加权组合柔顺度的小量变化约束、Heaviside密度映射和变约束限方案,建立了柔性机构构型平稳变化的优化模型;最后结合MMA算法,形成了一种构型平稳变化的柔性机构拓扑优化方法。给出的算例结果表明,相比于现有方法,该方法计算公式简单,可获得清晰且无类铰链的拓扑构型。
-
关键词:
- 柔性机构 /
- 拓扑优化 /
- Heaviside映射 /
- 柔顺度
Abstract: The existing methods for the topological optimization of a compliant mechanism still have some difficulties in optimizing its hinge-like and grey topology. In order to obtain a clear and optimal topology without any hinge, a structural topological optimization method is proposed. Firstly, we construct a weighted combination compliance function, which can comprehensively characterize the local stiffness characteristics of the input and output ends of the compliant mechanism. Then, by introducing the small change constraints of the weighted combination mechanism, the Heaviside density projection and a varied constraint scheme, we establish an optimization model with steady changes in the configuration of the compliant mechanism. Finally, in combination with the MMA algorithm, a topological optimization method for compliant mechanism with steady changes in configuration is formulated. The numerical simulation results show that, compared with the existing methods, the proposed method has simple calculation formulae and can obtain a clear optimal topology without hinges.-
Key words:
- compliant mechanism /
- topological optimization /
- Heaviside density projection /
-
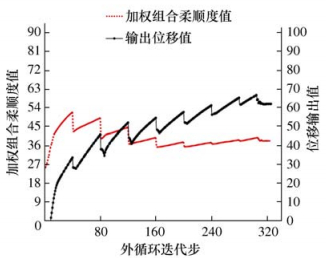
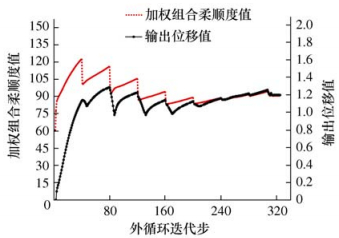
图 8 对应于图 7b)的位移反向结构的加权组合柔顺度和输出位移的优化历程曲线
表 1 不同α值和ε值时本文方法的输出位移值和Mnd值
特性值 α=0.6 α=1.0 0.005 0.010 0.025 0.005 0.010 0.025 输出位移值 60.215 61.789 75.534 59.064 61.456 74.761 Mnd值 0.001 63 0.001 34 0.002 55 0.001 47 0.00174 0.004 73 -
[1] Lau G K, Du H, Lim M K. Use of functional specifications as objective functions in topological optimization of compliant mechanism[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(34):4421-4433 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=c987d7248f8043481545be867ba22bf1 [2] Wang L P, Jiang Y, Li T M. Analytical compliance modeling of serial flexure-based compliant mechanism under arbitrary applied load[J]. Chinese Journal of Mechanical Engineering, 2017, 30(4):951-962 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jxgcxb-e201704018 [3] Chen G M, Liu X Y, Gao H W, et al. A generalized model for conic flexure hinges[J]. Review of Scientific Instruments, 2009, 80(5):055106 doi: 10.1063-1.3137074/ [4] Poulsen T A. A new scheme for imposing a minimum length scale in topology optimization[J]. International Journal for Numerical Methods in Engineering, 2003, 57(6):741-760 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1002/nme.694 [5] Yoon G H, Kim Y Y, Bendsoe M P, et al. Hinge-free topology optimization with embedded translation-invariant differentiable wavelet shrinkage[J]. Structural and Multidisciplinary Optimization, 2004, 27(3):139-150 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cdaa36a62b9839b23c5a499bbfe94dab [6] Yin L Z, Ananthasuresh G K. Design of distributed compliant mechanisms[J]. Mechanics Based Design of Structures and Machines, 2003, 31(2):151-179 http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_4b3845452f7b976774b30ea734b6bce3 [7] Sigmund O. Morphology-based black and white filters for topology optimization[J]. Structural and Multidisciplinary Optimization, 2007, 33(4-5):401-424 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cfb25fddfa941f981d38307f5e8fa84a [8] Luo J Z, Luo Z, Chen S K, et al. A new level set method for systematic design of hinge-free compliant mechanisms[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 198(2):318-331 doi: 10.1016-j.cma.2008.08.003/ [9] Wang M Y, Chen S K. Compliant mechanism optimization:analysis and design with intrinsic characteristic stiffness[J]. Mechanics Based Design of Structures and Machines, 2009, 37(2):183-200 http://cn.bing.com/academic/profile?id=5ffd1757431d32971a284490065373b9&encoded=0&v=paper_preview&mkt=zh-cn [10] Zhou H, Patil R B. The discrete topology optimization of structures using the improved hybrid discretization model[J]. Journal of Mechanical Design, 2012, 134(12):124503 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=0c92dc1a40496a6ce51e08097f86c17b [11] Zhu B L, Zhang X M, Wang N F. Topology optimization of hinge-free compliant mechanisms with multiple outputs using level set method[J]. Structural and Multidisciplinary Optimization, 2013, 47(5):659-672 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=d58d7808098f5af09285b032d5c5042c [12] Li L, Khandelwal K. Topology optimization of structures with length-scale effects using elasticity with microstructure theory[J]. Computers & Structures, 2015, 157:165-177 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=1499ae56fd0a448b8de88681113c1e24 [13] Lopes C G, Novotny A A. Topology design of compliant mechanisms with stress constraints based on the topological derivative concept[J]. Structural and Multidisciplinary Optimization, 2016, 54(4):737-746 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=6a6d9425f26b4514da76124dafca3d90 [14] 占金青, 龙良明, 刘敏, 等.基于最大应力约束的柔顺机构拓扑优化设计[J].机械工程学报, 2018, 54(23):32-38 http://d.old.wanfangdata.com.cn/Periodical/jxgcxb201823004Zhan J Q, Long L M, Liu M, et al. Topological design of compliant mechanisms with maximum stress constraint[J]. Journal of Mechanical Engineering, 2018, 54(23):32-38(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jxgcxb201823004 [15] Pereira A D A, Cardoso E L. On the influence of local and global stress constraint and filtering radius on the design of hinge-free compliant mechanisms[J]. Structural and Multidisciplinary Optimization, 2018, 58(2):641-655 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=949b45ab6d3b1b6250fc41799e6db179 [16] Rong J H, Yu L H, Rong X P, et al. A novel displacement constrained optimization approach for black and white structural topology designs under multiple load cases[J]. Structural and Multidisciplinary Optimization, 2017, 56(4):865-884 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=85a3feb2f0019876604cd3c745356454 [17] Guest J K, Prévost J H, Belytschko T. Achieving minimum length scale in topology optimization using nodal design variables and projection functions[J]. International Journal for Numerical Methods in Engineering, 2004, 61(2):238-254 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1002/nme.1064 [18] Schevenels M, Sigmund O. On the implementation and effectiveness of morphological close-open and open-close filters for topology optimization[J]. Structural and Multidisciplinary Optimization, 2016, 54(1):15-21 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=32d2a343410d24d6b8aa87b74424dc0c [19] Luo Z, Chen L P, Yang J Z, et al. Compliant mechanism design using multi-objective topology optimization scheme of continuum structures[J]. Structural and Multidisciplinary Optimization, 2005, 30(2):142-154 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a767b5207ba9c21d957ed54988a67fc9 [20] Svanberg K. A class of globally convergent optimization methods based on conservative convex separable approximations[J]. SIAM Journal on Optimization, 2002, 12(2):555-573 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=949a6b27e6b94580c9520a641fca20db -








 下载:
下载: