Analysis of Mixed-mode of Non-collinear Fatigue Crack Propagation
-
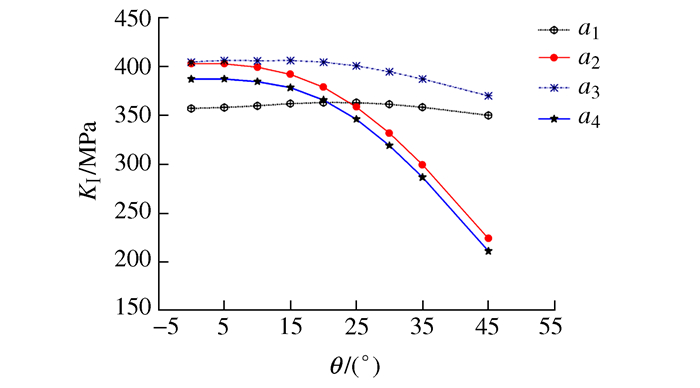
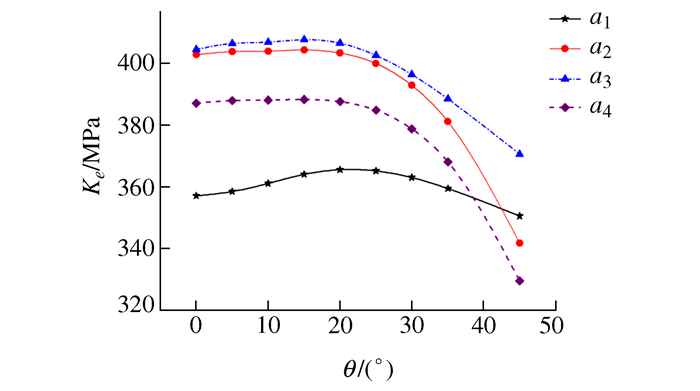
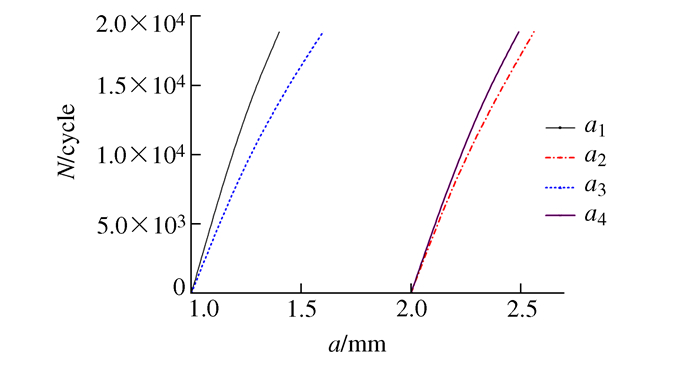
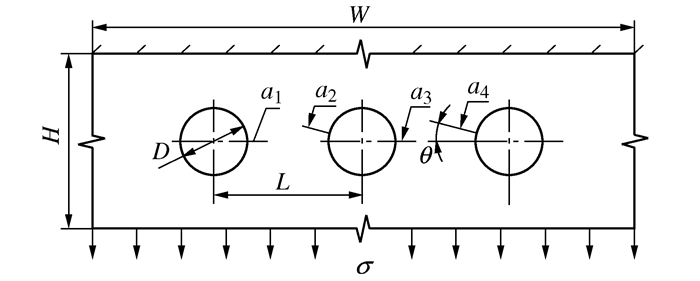
摘要: 以带多点损伤的空孔板为研究对象,利用数值分析法分析裂纹起裂位置和裂纹倾斜角对应力强度因子的影响,对比了共线多裂纹与非共线复合型裂纹起始扩展速率和扩展寿命的差异。结果表明:非共线复合型裂纹起始扩展速率偏大,裂纹扩展寿命缩短约2.5%。在非共线复合型裂纹模型中,随着裂纹倾斜角增加,等效应力强度因子先增大后减小,且在15°时,整体裂纹扩展速率达最大值。相邻孔间裂纹的相对位置和相对方位影响裂纹的扩展路径,进而影响裂纹扩展寿命。Abstract: Taking hollowed pre-notched plate with multiple-site damages (MSD) as study object, the influence of crack initiation positions and angles on the stress intensity factor was investigated using numerical analysis method in the paper. And the differences of the initial propagation rate and propagation life between the collinear multi-crack and non-collinear multi-mixed crack were also performed. The results indicated that, for the non-collinear mixed-crack, the initial propagation rate of crack was larger, while its propagation life was shortened by about two point five percent; moreover the equivalent stress intensity factor initially increased, followed by decreases as the crack angles increased. The overall crack propagation rate reached the maximum as the crack angle 15°. In addition, the relative position and relative orientation of the cracks between adjacent holes influenced their propagation paths, which would effect on the crack propagation life.
-
表 1 2024-T3材料力学参数和模型几何参数
力学性能参数 几何参数 弹性模量/GPa 75 a1/mm 1 泊松比 0.32 a2/mm 2 板高H/mm 200 a3/mm 1 板宽W/mm 50 a4/mm 2 板厚d/mm 1.6 裂纹倾斜角θ/(°) 0/5/10/15/20/
25/30/35/45孔径D/mm 4 σmax/MPa 100 间距L/mm 10 R 0.01 σys/MPa 330.9 -
[1] FAA. Establishing and implementing limit of validity to prevent widespread fatigue damage[S]. Renton Washington: FAA, 2011 [2] 贾宝惠, 刘彦波, 卢翔, 等.低利用率下民机结构维修间隔确定模型[J].航空学报, 2018, 39(1):215-225 http://d.old.wanfangdata.com.cn/Periodical/hkxb201801019Jia B H, Liu Y B, Lu X, et al. Model for determining maintenance intervals of aircraft structural with low utilization[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(1):215-225 (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/hkxb201801019 [3] 刘金祥, 张华阳, 李军.基于扩展有限元法的Ⅰ-Ⅱ复合型裂纹扩展研究[J].北京理工大学学报, 2015, 35(9):881-885 http://d.old.wanfangdata.com.cn/Periodical/bjlgdxxb201509001Liu J X, Zhang H Y, Li J. Study on Ⅰ-Ⅱ mixed mode crack growth using extended finite element method[J]. Transactions of Beijing Institute of Technology, 2015, 35(9):881-885 (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/bjlgdxxb201509001 [4] Kebir H, Roelandt J M, Chambon L. Dual boundary element method modelling of aircraft structural joints with multiple site damage[J]. Engineering Fracture Mechanics, 2006, 73(4):418-434 doi: 10.1016/j.engfracmech.2005.08.006 [5] Jones R, Molent L, Pitt S. Understanding crack growth in fuselage lap joints[J]. Theoretical and Applied Fracture Mechanics, 2008, 49(1):38-50 doi: 10.1016/j.tafmec.2007.10.002 [6] Millwater H R. A simple and accurate method for computing stress intensity factors of collinear interacting cracks[J]. Aerospace Science and Technology, 2010, 14(8):542-550 doi: 10.1016/j.ast.2010.04.003 [7] Kastratović G, Grbović A, Vidanović N. Approximate method for stress intensity factors determination in case of multiple site damage[J]. Applied Mathematical Modelling, 2015, 39(19):6050-6059 doi: 10.1016/j.apm.2015.01.050 [8] 谭晓明, 陈跃良, 段成美.三维多裂纹应力强度因子的有限元分析[J].机械强度, 2004, 26(S1):195-198 http://d.old.wanfangdata.com.cn/Periodical/jxqd2004z1057Tan X M, Chen Y L, Duan C M. Analysis of stress intensity factors of 3-D multiple cracks using finite element method[J]. Journal of Mechanical Strength, 2004, 26(S1):195-198 (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jxqd2004z1057 [9] 任克亮, 吕国志.三维广布裂纹应力强度因子求解[J].航空学报, 2008, 29(4):893-897 doi: 10.3321/j.issn:1000-6893.2008.04.020Ren K L, Lü G Z. Solution for stress intensity factors of three dimensional widespread cracks[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(4):893-897 (in Chinese) doi: 10.3321/j.issn:1000-6893.2008.04.020 [10] 刘金祥, 张华阳, 李军.基于扩展有限元法的Ⅰ-Ⅱ复合型裂纹扩展研究[J].北京理工大学学报, 2015, 35(9):881-885 http://d.old.wanfangdata.com.cn/Periodical/bjlgdxxb201509001Liu J X, Zhang H Y, Li J. Study on Ⅰ-Ⅱ mixed mode crack growth using extended finite element method[J]. Transactions of Beijing Institute of Technology, 2015, 35(9):881-885 (in Chinese) http://d.old.wanfangdata.com.cn/Periodical/bjlgdxxb201509001 [11] 苏毅, 王生楠, 闫晓中.四结点等参元XFEM程序设计及在裂纹问题中的应用[J].机械科学与技术, 2012, 31(12):1949-1954 http://journals.nwpu.edu.cn/jxkxyjs/CN/abstract/abstract5448.shtmlSu Y, Wang S N, Yan X Z. XFEM programming for four nodes isoparametric element and its application in crack problems[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(12):1949-1954 (in Chinese) http://journals.nwpu.edu.cn/jxkxyjs/CN/abstract/abstract5448.shtml [12] Wu X R, Xu W. Strip yield crack analysis for multiple site damage in infinite and finite panels a weight function approach[J]. Engineering Fracture Mechanics, 2011, 78(14):2585-2596 doi: 10.1016/j.engfracmech.2011.06.016 [13] Zhao J F, Xie L Y, Liu J Z, et al. A method for stress intensity factor calculation of infinite plate containing multiple hole-edge cracks[J]. International Journal of Fatigue, 2012, 35(1):2-9 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=b888b616ea65c94101fd4a8653272f36 [14] 郁大照, 陈跃良, 王允良.含多处损伤宽板螺接搭接件疲劳寿命研究[J].工程力学, 2017, 34(6):217-225 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gclx201706023Yu D Z, Chen Y L, Wang Y L. Study on fatigue life of wide bolted lap joint with multiple site damage[J]. Engineering Mechanics, 2017, 34(6):217-225 (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gclx201706023 [15] 陈跃良, 郁大照, 杨茂胜, 等.含多处损伤搭接结构应力强度因子有限元分析[J].航空学报, 2007, 28(3):615-619 doi: 10.3321/j.issn:1000-6893.2007.03.022Chen Y L, Yu D Z, Yang M S, et al. Finite element analysis of stress intensity factors of lap joint with multiple site damage[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(3):615-619 (in Chinese) doi: 10.3321/j.issn:1000-6893.2007.03.022 [16] Moёs N, Dolbow J, Belytschko T. A finite element method for crack growth without remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 46(1):131-150 doi: 10.1002/(ISSN)1097-0207 [17] 任克亮, 吕国志.老龄化结构表面裂纹间相关性分析与研究[J].力学与实践, 2007, 29(4):55-58, 62 doi: 10.3969/j.issn.1000-0879.2007.04.013Ren K L, Lü G Z. Relativity analysis and research on the surface crack in aging structure[J]. Mechanics in Engineering, 2007, 29(4):55-58, 62 (in Chinese) doi: 10.3969/j.issn.1000-0879.2007.04.013 [18] Newman Jr J C, Ramakrishnan R. Fatigue and crack-growth analyses of riveted lap-joints in a retired aircraft[J]. International Journal of Fatigue, 2016, 82:342-349 doi: 10.1016/j.ijfatigue.2015.04.010 [19] Newman Jr J C. A crack opening stress equation for fatigue crack growth[J]. International Journal of Fracture, 1984, 24(4):R131-R135 doi: 10.1007/BF00020751 [20] Elber W. The significance of fatigue crack closure[J]. ASTM STP, 1971, 486:230-242 doi: 10.1520-STP26680S/ [21] Spagnoli A. Self-similarity and fractals in the Paris range of fatigue crack growth[J]. Mechanics of Materials, 2005, 37(5):519-529 doi: 10.1016/j.mechmat.2004.04.003 [22] 郦正能.应用断裂力学[M].北京:北京航空航天大学出版社, 2012Li Z N. Application of fracture mechanics[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2012 (in Chinese) [23] Silva L F M, Gonçalves J P M, Oliveira F M F, et al. Multiple-site damage in riveted lap-joints: experimental simulation and finite element prediction[J]. International Journal of Fatigue, 2000, 22(4):319-338 doi: 10.1016/S0142-1123(99)00129-2 -







 下载:
下载: