Application of Cellular Automata Theory in the Search Method of Workspace of Parallel Manipulator
-
摘要: 针对传统并联机构工作空间搜索法所得边界精度低、效率低等问题,提出一种通用的基于元胞自动机理论的快速搜索方法。该方法以元胞自动机中邻域思想和黄金分割法原理为基础,研究了并联机构工作空间求解的数值法,并总结出这些方法的不足。通过引入元胞自动机的邻域提取粗糙化边界和搜索方向,并将黄金分割二分法引入维度搜索中,以实现任意精度的边界点搜索,其后仿真算例检验了此方法的有效性与快速性,并与极坐标搜索法、蒙特卡洛法、精确化处理进行对比。分析表明:该算法在求解精度、效率具有明显优势,并且适用于二维、三维的并联机构工作空间的求解。Abstract: In terms of the traditional search method of workspace having the boundary problem of low accuracy and low efficiency, a general fast search method was put forward via the theory of cellular automata. This algorithm based on the thought of neighborhood of cellular automata and the golden section method. First, the traditional numerical methods of the workspace of parallel mechanism were studied and summarized their deficiency; the method introduced the neighborhood of cellular automata so as to extract roughness boundary and the search direction. Then, the golden section method was introduced into dimension search so as to realize search of arbitrary precision of boundary point. The quickness and the effectiveness of algorithm are tested by simulation examples, and compared with polar coordinate searching method, Monte Carlo method and the process of precision processing show that the algorithm has obvious advantages in the accuracy and efficiency, and is suitable for 2D or 3D the workspace problems of parallel manipulator.
-
Key words:
- parallel manipulator /
- workspace /
- cellular automaton /
- neighborhood /
- golden section method
-
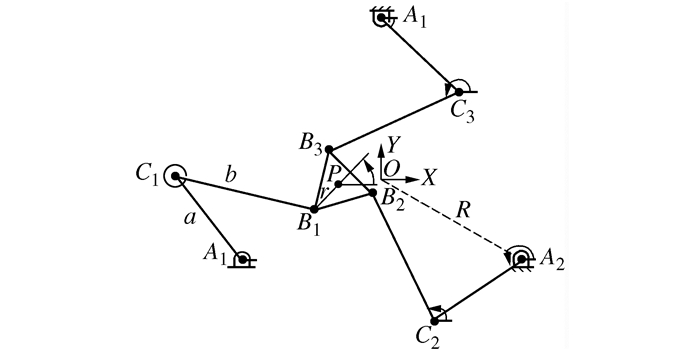
表 1 3RRR平面并联机构参数值
m R r a b 
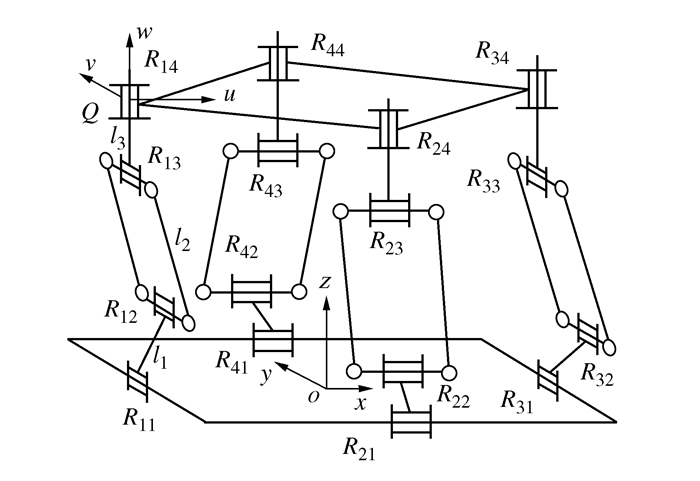
1 1.75 2.25 表 2 3T1R平面并联机构参数值
m R r l1 l2 l3 1.0 0.8 0.7 2.0 0.419 1 表 3 极坐标边界搜索法与元胞黄金分割法对比
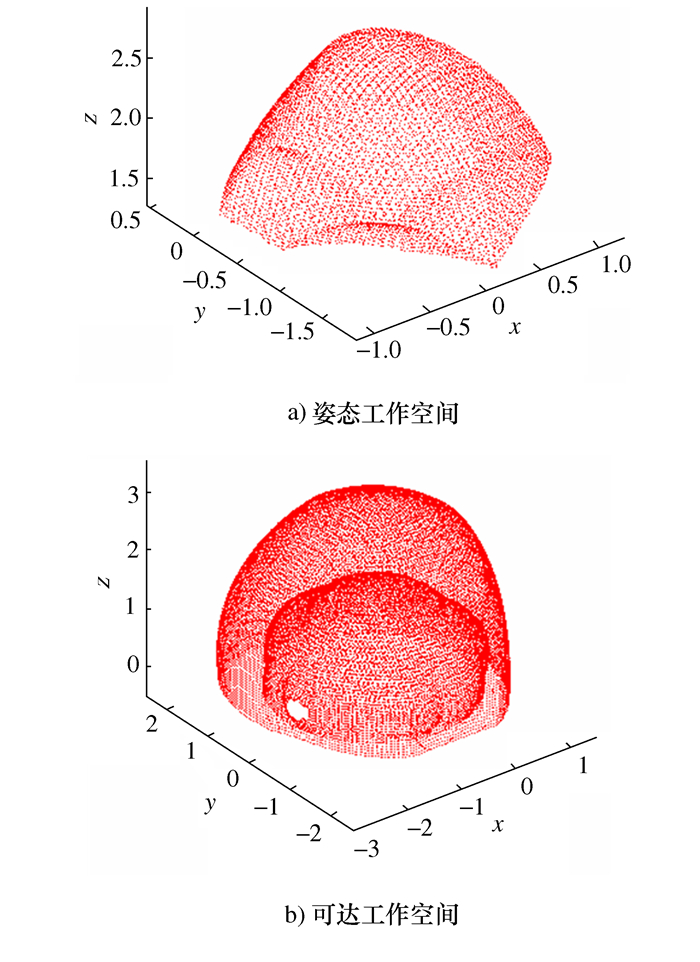
a 算法 可达工作空间耗时 姿态工作空间耗时 极坐标搜索法 677.222 105 39.776 22 元胞黄金分割法 2.328 487 0.823 79 表 4 蒙特卡洛法算法与元胞黄金分割法对比
s 算法 可达工作空间耗时 姿态工作空间耗时 蒙特卡洛法 90.168 225 48.752 804 元胞黄金分割法 46.480 772 9.767 137 -
[1] 沈惠平, 张震, 杨廷力, 等.3T1R并联机构结构降耦设计与其运动学分析[J].农业机械学报, 2017, 48(10):380-389, 400 doi: 10.6041/j.issn.1000-1298.2017.10.049Shen H P, Zhang Z, Yang T L, et al. Structure coupling-reducing design and kinematics analysis of 3T1R parallel mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(10):380-389, 400(in Chinese) doi: 10.6041/j.issn.1000-1298.2017.10.049 [2] Cao Y, Lu K, Li X J, et al. Accurate numerical methods for computing 2D and 3D robot workspace[J]. International Journal of Advanced Robotic Systems, 2011, 8(6):1-13 http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_9f24247b8c1858bf6b77cb7737b14646 [3] 赵燕江, 张永德, 姜金刚, 等.基于Matlab的机器人工作空间求解方法[J].机械科学与技术, 2009, 28(12):1657-1661, 1666 http://www.cnki.com.cn/Article/CJFDTotal-JXKX200912027.htmZhao Y J, Zhang Y D, Jiang J G, et al. A method for solving robot workspace based on matlab[J]. Mechanical Science and Technology for Aerospace Engineering, 2009, 28(12):1657-1661, 1666(in Chinese) http://www.cnki.com.cn/Article/CJFDTotal-JXKX200912027.htm [4] 崔建昆.3-RRR平面并联机器人的灵活工作空间[J].上海理工大学学报, 2005, 27(4):365-368, 372 doi: 10.3969/j.issn.1007-6735.2005.04.021Cui J K. On the dexterous workspace of 3-RRR planar parallel manipulator[J]. Journal of University of Shanghai for Science and Technology, 2005, 27(4):365-368, 372(in Chinese) doi: 10.3969/j.issn.1007-6735.2005.04.021 [5] Bonev I A, Ryu J. A geometrical method for computing the constant-orientation workspace of 6-PRRS parallel manipulators[J]. Mechanism and Machine Theory, 2001, 36(1):1-13 doi: 10.1016/S0094-114X(00)00031-8 [6] 宋亚楠, 崔建昆.求解平面并联机器人工作空间边界的折返式搜索算法[J].机械传动, 2015, 39(5):70-72 http://www.cnki.com.cn/Article/CJFDTOTAL-JXCD201505038.htmSong Y N, Cui J K. Iterative search algorithm for solving planar parallel robot workspace boundary[J]. Journal of Mechanical Transmission, 2015, 39(5):70-72(in Chinese) http://www.cnki.com.cn/Article/CJFDTOTAL-JXCD201505038.htm [7] 朱心平, 崔建昆, 张源.求解3-RRR平面并联机器人工作空间的迭代搜索法[J].机械研究与应用, 2010(3):48-49 doi: 10.3969/j.issn.1007-4414.2010.03.020Zhu X P, Cui J K, Zhang Y. Iterative search research on work space for 3-RRR paralleled robot mechanism[J]. Mechanical Research & Application, 2010(3):48-49(in Chinese) doi: 10.3969/j.issn.1007-4414.2010.03.020 [8] Snyman J A, du Plessis L J, Duffy J. An optimization approach to the determination of the boundaries of manipulator workspaces[J]. Journal of Mechanical Design, 2000, 122(4):447-456 doi: 10.1115/1.1289388 [9] Huang M Z, Thebert J L. A study of workspace and singularity characteristics for design of 3-DOF planar parallel robots[J]. The International Journal of Advanced Manufacturing Technology, 2010, 51(5-8):789-797 doi: 10.1007/s00170-010-2632-4 [10] Huang M Z, Thebert J L. A study of workspace and singularity characteristics for design of 3-DOF planar parallel robots[J]. The International Journal of Advanced Manufacturing Technology, 2010, 51(5-8):789-797 doi: 10.1007/s00170-010-2632-4 [11] 朱海飞, 管贻生, 吴文强, 等.基于二分逼近原理的定姿态工作空间快速搜索方法[J].机器人, 2013, 35(6):709-715 http://d.old.wanfangdata.com.cn/Periodical/jqr201306010Zhu H F, Guan Y S, Wu W Q, et al. A fast search method for computing the constant-orientation workspace based on the binary approximating principle[J]. Robot, 2013, 35(6):709-715(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jqr201306010 [12] Alciatore D, Ng C. Determining manipulator workspace boundaries using the Monte Carlo method and least squares segmentation[J]. ASME Robotics:Kinematics, Dynamics and Controls, 1994, 72:141-146 [13] Cao Y, Zang H, Wu L, et al. An engineering oriented method for the three dimensional workspace generation of robot manipulator[J]. Journal of Information and Computational Science, 2011, 8(1):51-61 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=7d8005a3b0f95813f0ea57123a71a788 [14] 王燕, 杨庆华, 鲍官军, 等.关节型果蔬采摘机械臂优化设计与试验[J].农业机械学报, 2011, 42(7):191-195 http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201107036Wang Y, Yang Q H, Bao G J, et al. Optimization design and experiment of fruit and vegetable picking manipulator[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(7):191-195(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201107036 [15] Zaitsev D A. A generalized neighborhood for cellular automata[J]. Theoretical Computer Science, 2016, 666:21-35 [16] Frette O I, Virnovsky G, Silin D. Estimation of the curvature of an interface from a digital 2D image[J]. Computational Materials Science, 2009, 44(3):867-875 doi: 10.1016/j.commatsci.2008.06.006 [17] Ding X F, Guo H, Guo S. Efficiency enhancement of traction system based on loss models and golden section search in electric vehicle[J]. Energy Procedia, 2017, 105:2923-2928 doi: 10.1016/j.egypro.2017.03.662 [18] 石志新, 叶梅燕, 罗玉峰, 等.3T1R并联机构结构设计与位置分析[J].农业机械学报, 2016, 47(8):364-369 http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201608048Shi Z X, Ye M Y, Luo Y F, et al. Structure design and displacement analysis of 3T1R parallel mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(8):364-369(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201608048 [19] 王阳, 郭林福.轻型协作机械臂运动学及工作空间分析[J].机械工程与自动化, 2017(1):44-46 doi: 10.3969/j.issn.1672-6413.2017.01.018Wang Y, Guo L F. Kinematics and workspace analysis of lightweight collaboration manipulator[J]. Mechanical Engineering & Automation, 2017(1):44-46(in Chinese) doi: 10.3969/j.issn.1672-6413.2017.01.018 [20] 刘志忠, 柳洪义, 罗忠, 等.机器人工作空间求解的蒙特卡洛法改进[J].农业机械学报, 2013, 44(1):230-235 http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201301043Liu Z Z, Liu H Y, Luo Z, et al. Improvement on monte carlo method for robot workspace determination[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(1):230-235(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201301043 -








 下载:
下载: