Fast Approximation Algorithm of N-Degree Bezier Curve via Polygon
-
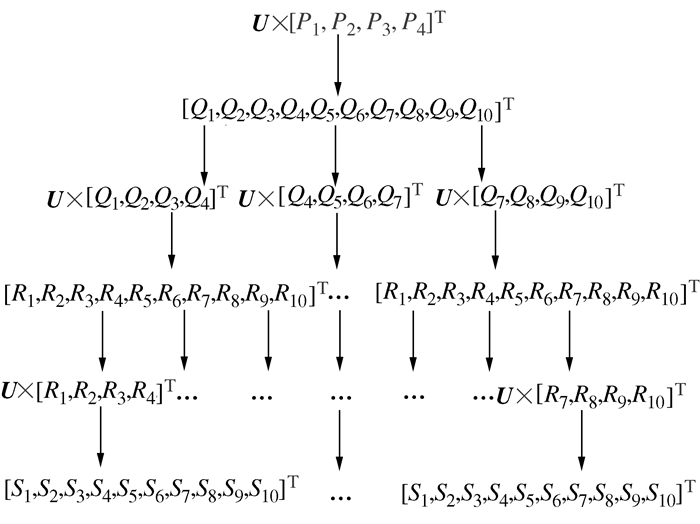
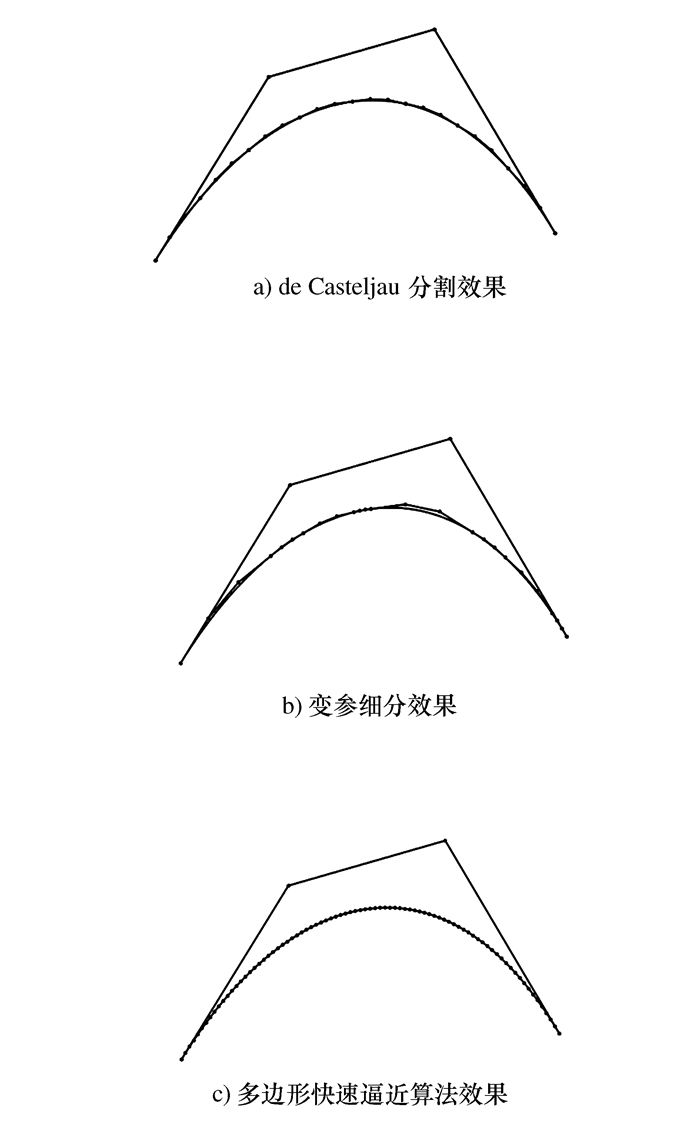
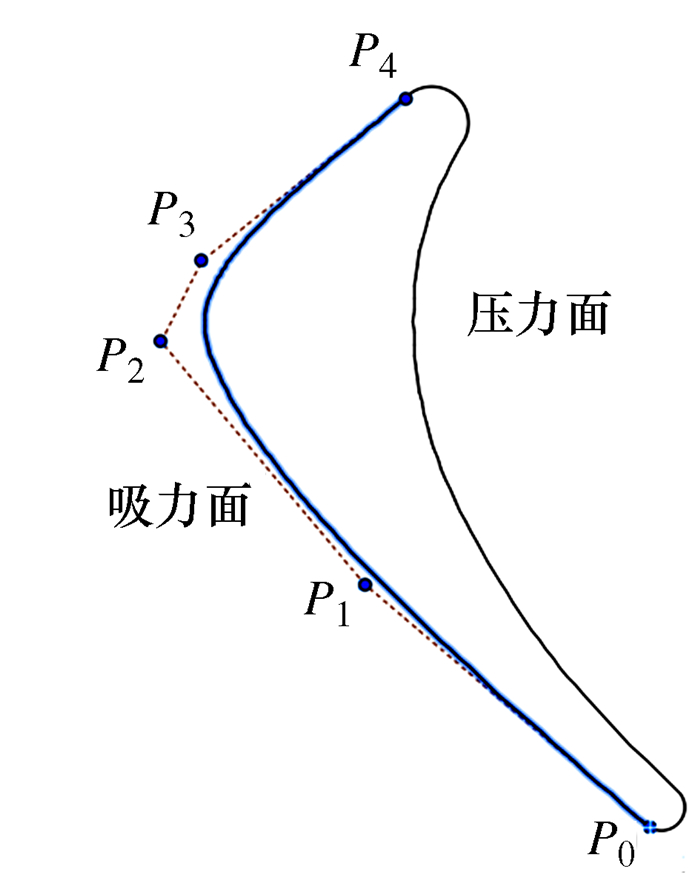
摘要: 作为一种重要的形状表示的数学方法,Bezier曲线在各种CAD/CAM(计算机辅助设计和计算机辅助制造)软件中广泛应用。在复杂曲面的数控加工操作中,CAD/CAM系统最终以直线段代替曲线段进行加工。为了提高以微小直线段逼近Bezier曲线的效率和精度,提出了一种对于N次Bezier曲线较为实用的快速逼近算法。该方法通过对Bezier曲线反复进行定比分割,使其控制多边形逐步收敛于原Bezier曲线,直至逼近误差满足要求。通过MATLAB软件将该算法与已有分割算法进行对比,结果表明与已有分割算法相比,多边形快速逼近算法极大地降低了逼近误差,较好的提高分割效率。最后,通过给出工程实例验证了该算法在工程应用上的实用性。Abstract: As an important mathematical method of shape representation, Bezier curve is widely used in CAD/CAM software. In the numerical control machining operation of complex surface, the CAD/CAM (computer-aided design, computer-aided manufacturing) system eventually uses the straight line segments instead of the curve to process a workpiece. In order to improve the efficiency and accuracy of approximation Bezier curve with tiny straight line segments, a fast approximation algorithm for N-degree Bezier curve is proposed. In this method, the Bezier curve is subdivided with an invariable proportion repeatedly to make the control polygon converge gradually to the original Bezier curve until the approximation error meets the requirement. Comparing with the existing segmentation algorithm by using MATLAB software, the results show that the fast approximation algorithm via polygon reduces greatly the approximation error and improves the segmentation efficiency. Finally, the practicality of this algorithm in engineering is verified by giving an example.
-
Key words:
- Bezier curve /
- approximation algorithm /
- segmentation algorithm /
- efficiency
-
表 1 三种分割算法不同次数分割效果对比
分割次数 分割算法 平均时间/
(×10-7 s)离散点数 逼近误差 每点时耗/
(×10-7 s)分
割
三
次de Casteljau算法 3.3 25 0.468 7 13.20 变参细分算法 3.3 25 1.932 6 13.20 快速逼近算法 4.9 82 0.0413 5.96 分割四次 de Casteljau算法 5.2 49 0.1176 10.61 变参细分算法 5.3 49 1.2215 10.81 快速逼近算法 11.6 244 0.0046 4.75 分割五次 de Casteljau算法 10.1 97 0.0294 10.41 变参细分算法 10.2 97 0.8416 10.52 快速逼近算法 31.2 730 0.0005 4.27 -
[1] Li Y W, Zhang C Z. A study of Bezier curve used in CNC based on DSP and FPGA[J]. Journal of Computer, 2016, 27(2):1-11 http://www.csroc.org.tw/journal/JOC27_2/JOC27-2-1.pdf [2] 孙海洋, 范大鹏, 李玲.一种参数曲线实时数控插补计算新方法[J].国防科技大学学报, 2008, 30(3):122-127 doi: 10.3969/j.issn.1001-2486.2008.03.024Sun H Y, Fan D P, Li L. A novel method for real-time CNC curved path interpolation calculating[J]. Journal of National University of Defense Technology, 2008, 30(3):122-127(in Chinese) doi: 10.3969/j.issn.1001-2486.2008.03.024 [3] 叶丽, 谢明红.三次Bezier曲线的插补算法及误差分析[J].重庆工学院学报(自然科学版), 2008, 22(7):34-39 doi: 10.3969/j.issn.1674-8425-B.2008.07.009Ye L, Xie M H. Cubic Bezier curve interpolation algorithm and its error analysis[J]. Journal of Chongqing Institute of Technology (Natural Science), 2008, 22(7):34-39(in Chinese) doi: 10.3969/j.issn.1674-8425-B.2008.07.009 [4] 宋健, 桑运晓, 刘同壮.一种基于de Casteljau算法的Bezier曲线插补方法[J].山东工业技术, 2017, (12):242 http://d.old.wanfangdata.com.cn/Periodical/sdgyjs201712221Song J, Sang Y X, Liu T Z. A Bezier curve interpolation method based on de Casteljau algorithm[J]. Shandong Industrial Technology, 2017, (12):242(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/sdgyjs201712221 [5] 任敏.绘制Bezier曲线的算法研究[J].现代机械, 2007, (1):65-76 doi: 10.3969/j.issn.1002-6886.2007.01.027Ren M. The Bezier curve expression algorithm research[J]. Modern Machinery, 2007, (1):65-76(in Chinese) doi: 10.3969/j.issn.1002-6886.2007.01.027 [6] 冯高洁, 张平.基于De_Boor递推算法的速度自适应NURBS曲线分段插补算法研究[J].机床与液压, 2011, 39(21):35-38 doi: 10.3969/j.issn.1001-3881.2011.21.009Feng G J, Zhang P. Study on segmented velocity adaptive NURBS interpolation algorithm based on De_Boor recursion algorithm[J]. Machine Tool & Hydraulics, 2011, 39(21):35-38(in Chinese) doi: 10.3969/j.issn.1001-3881.2011.21.009 [7] 郭峰, 李伟, 张来宾, 等.Bezier曲线参数化高精度插补的研究与实现[J].机械制造, 2012, 50(6):31-33 http://d.old.wanfangdata.com.cn/Periodical/jxzz201206011Guo F, Li W, Zhang L B, et al. Research and implementation of Bezier curve parameterized high precision interpolation[J]. Machinery, 2012, 50(6):31-33(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jxzz201206011 [8] 马瑞海, 邱泽阳.Bézier曲线的升阶方法[J].黑龙江科技学院学报, 2010, 20(6):481-482, 487 doi: 10.3969/j.issn.1671-0118.2010.06.020Ma R H, Qiu Z Y. Method for degree elevation of Bézier curve[J]. Journal of Heilongjiang Institute of Science & Technology, 2010, 20(6):481-482, 487(in Chinese) doi: 10.3969/j.issn.1671-0118.2010.06.020 [9] Goldman R. An integrated introduction to computer graphics and geometric modeling[M]. Boca Raton:CRC Press, 2009 [10] Morin G, Goldman R. On the smooth convergence of subdivision and degree elevation for Bézier curves[J]. Computer Aided Geometric Design, 2001, 18(7):657-666 doi: 10.1016/S0167-8396(01)00059-0 [11] 徐雨明, 文双春. Bezier曲线递归分割算法的研究[J].衡阳师范学院学报, 2007, 28(6):113-115 doi: 10.3969/j.issn.1673-0313.2007.06.029Xu Y M, Wen S C. Study on Bezier curve recursive algorithm[J]. Journal of Hengyang Normal University, 2007, 28(6):113-115(in Chinese) doi: 10.3969/j.issn.1673-0313.2007.06.029 [12] 冯文月, 吴梦, 邓建松.Bézier曲线细分收敛定理的推广[J].计算机辅助设计与图形学报, 2011, 23(12):2000-2005 http://d.old.wanfangdata.com.cn/Periodical/jsjfzsjytxxxb201112008Feng W Y, Wu M, Deng J S. Generalization of subdivision convergence of Bézier curves[J]. Journal of Computer-Aided Design & Computer Graphics, 2011, 23(12):2000-2005(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jsjfzsjytxxxb201112008 [13] 韩丽娜, 张红祥, 张群会. Bezier曲线修改的一种分割算法[J].计算机工程与科学, 2006, 28(7):77-79 doi: 10.3969/j.issn.1007-130X.2006.07.024Han L N, Zhang H X, Zhang Q H. A segmentation method for modifying the Bezier curve[J]. Computer Engineering & Science, 2006, 28(7):77-79(in Chinese) doi: 10.3969/j.issn.1007-130X.2006.07.024 [14] Elhoseny M, Tharwat A, Hassanien A E. Bezier curve based path planning in a dynamic field using modified genetic algorithm[J]. Journal of Computational Science, 2018, 25:339-350 doi: 10.1016/j.jocs.2017.08.004 [15] Li B L, Liu L J, Zhang Q H, et al. Path planning based on firefly algorithm and Bezier curve[C]//Proceedings of 2014 IEEE International Conference on Information and Automation. Hailar, China: IEEE, 2014: 630-633 -








 下载:
下载: