Truss Topology Optimization with Buckling Constraints Solved by Multi-point Approximation and Genetic Algorithm
-
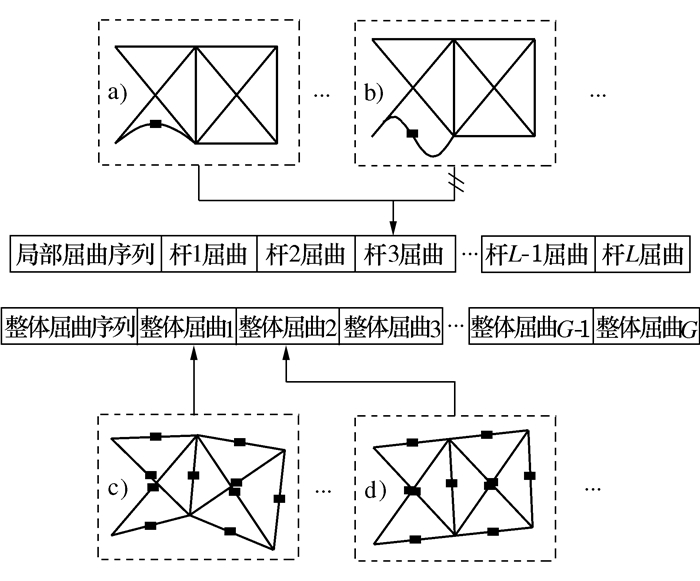
摘要: 基于线弹性屈曲理论,讨论了杆单元建模及欧拉单杆失稳判据在桁架结构稳定性分析中的缺陷。为更精确地获得桁架屈曲响应,建议以梁单元进行有限元建模,并利用特征值屈曲分析来获取结构各阶失稳载荷因子及屈曲模态。分析了从基结构法出发求解特征值屈曲约束下桁架拓扑优化问题所存在的求解困难与奇异性。为有效求解该类问题,采用了多点逼近遗传算法,对离散拓扑变量和连续尺寸变量进行了联合优化。同时,通过屈曲模态识别、删除杆件屈曲模态过滤、局部约束临时删除等措施,特征值约束下的求解困难和删除杆件在优化过程中的不利影响也得到了克服。数值算例验证了本文结构建模及优化方法的有效性,同时也表明了该方法具有较高的效率,能够凭借较少的结构分析次数来获得优化解。Abstract: Based on the elastic buckling theory, the paper discussed the insufficiency of rod elements with Euler buckling criterion while conducting the stability analysis for truss structures. In order to obtain relatively more accurate buckling responses, beam elements were supposed to be adopted in truss modeling. After that, buckling load factors as well as buckling modes could be obtained via eigenvalue buckling analysis. Then, from the point of ground structure method, the paper pointed some solving difficulties and the singularity of truss topology optimization problems under eigenvalue buckling constraints. To handle such problems effectively, the multi-point approximation algorithm combined with genetic algorithm was implemented to optimize both the discrete topology variables and the continuous sizing variables coordinately. In the meantime, several techniques, such as recognition of buckling modes, filtration of buckling on removed bars, temporary deletion of local constraints, were proposed and applied to tackle the solving difficulties and the singularity. At last, the effectiveness of the optimization strategy was verified by numerical examples. Besides, the efficiency of the method was also presented as the optimization could be achieved through relatively small number of structural analysis.
-
Key words:
- truss structures /
- topology optimization /
- buckling constraints /
- approximation algorithms /
- genetic
-
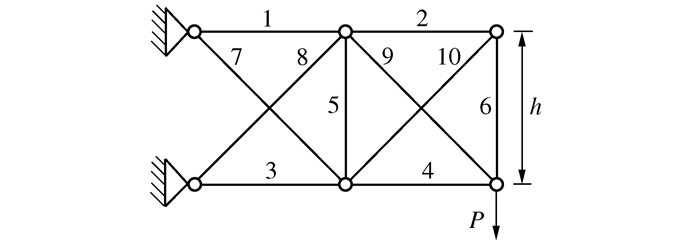
表 1 十杆平面桁架结构参数
几何参数h 载荷P 截面积 弹性模量 泊松比 914.4 cm 50 kN 100 cm2 68.96 Gpa 0.3 表 2 删除杆件对桁架屈曲分析结果的影响对比
模态阶数 保留杆10单元 去除杆10单元 屈曲因子 屈曲杆件 屈曲因子 屈曲杆件 1 3.03×10-6 杆10 0.821 杆8 2 1.21×10-5 杆10 0.898 杆3 3 2.73×10-5 杆10 1.295 杆4 4 4.87×10-5 杆10 2.929 杆5 5 7.64×10-5 杆10 3.284 杆8 6 1.11×10-4 杆10 3.590 杆3 7 1.53×10-4 杆10 5.177 杆4 8 2.02×10-4 杆10 7.390 杆8 9 2.60×10-4 杆10 8.073 杆3 10 3.69×10-4 杆10 11.643 杆4 11 4.31×10-4 杆10 11.707 杆5 12 5.32×10-4 杆10 13.154 杆8 13 6.58×10-4 杆10 14.357 杆3 14 8.09×10-4 杆10 20.618 杆8 15 9.89×10-4 杆10 20.707 杆4 16 1.20×10-3 杆10 22.481 杆3 17 1.42×10-3 杆10 26.328 杆5 18 1.63×10-3 杆10 29.869 杆8 19 1.79×10-3 杆10 32.423 杆4 20 1.84×10-3 杆10 32.526 杆3 21 0.821 杆8 41.044 杆8 22 0.898 杆3 44.629 杆3 23 1.295 杆4 46.822 杆5 24 2.929 杆5 46.910 杆4 25 3.284 杆8 54.312 杆8 26 3.590 杆3 58.946 杆3 27 5.177 杆4 64.365 杆4 28 7.390 杆8 69.622 杆8 29 8.073 杆3 73.314 杆5 30 11.643 杆4 75.343 杆3 表 3 十杆平面桁架优化结果
杆件 截面积/cm2 截面半径/cm 轴向应力/MPa 1 4.985 1.260 100.30 2 4.993 1.261 100.14 3 124.653 6.299 -8.02 4 3.142 1.000 0 5 3.142 1.000 0 6 4.993 1.261 100.14 7 7.113 1.505 99.41 8 0 0 - 9 0 0 - 10 147.613 6.855 -4.79 表 4 十杆平面桁架优化后前十阶屈曲因子
模态阶数 屈曲因子 1 0.998 2 1.006 3 3.990 4 4.021 5 8.976 6 9.040 7 15.970 8 16.070 9 25.020 10 25.150 -
[1] Dorn W S. Automatic design of optimal structures[J]. Journal De Mecanique, 1964, 3:25-52 [2] Cheng G D, Jiang Z. Study on topology optimization with stress constraints[J]. Engineering Optimization, 1992, 20(2):129-148 doi: 10.1080-03052159208941276/ [3] Cheng G. Some aspects of truss topology optimization[J]. Structural Optimization, 1995, 10(3-4):173-179 doi: 10.1007/BF01742589 [4] Cheng G, Guo X, Olhoff N. New formulation for truss topology optimization problems under buckling constraints[M]//Rozvany G I N, Olhoff N. Topology Optimization of Structures and Composite Continua. Dordrecht: Kluwer Academic Publishers, 2000 [5] Rozvany G I N. Difficulties in truss topology optimization with stress, local buckling and system stability constraints[J]. Structural Optimization, 1996, 11(3-4):213-217 doi: 10.1007/BF01197036 [6] Zhou M. Difficulties in truss topology optimization with stress and local buckling constraints[J]. Structural Optimization, 1996, 11(2):134-136 doi: 10.1007/BF01376857 [7] 邹文胜, 左正兴, 廖日东, 等.考虑压杆稳定性的桁架拓扑优化设计[J].北京理工大学学报, 1999, 19(1):29-33 doi: 10.3969/j.issn.1001-0645.1999.01.007Zou W S, Zuo Z X, Liao R D, et al. Truss topology optimization considering structural stability[J]. Journal of Beijing Institute of Technology, 1999, 19(1):29-33(in Chinese) doi: 10.3969/j.issn.1001-0645.1999.01.007 [8] Guo X, Cheng G, Yamazaki K. A new approach for the solution of singular optima in truss topology optimization with stress and local buckling constraints[J]. Structural and Multidisciplinary Optimization, 2001, 22(5):364-373 doi: 10.1007/s00158-001-0156-0 [9] 唐文艳, 袁清珂.屈曲约束桁架拓扑优化的遗传算法[J].机械科学与技术, 2009, 28(4):460-463 doi: 10.3321/j.issn:1003-8728.2009.04.009Tang W Y, Yuan Q K. An improved genetic algorithm for topology optimization of a truss under local buckling constraints[J]. Mechanical Science and Technology for Aerospace Engineering, 2009, 28(4):460-463(in Chinese) doi: 10.3321/j.issn:1003-8728.2009.04.009 [10] Koĉvara M. On the modelling and solving of the truss design problem with global stability constraints[J]. Structural and Multidisciplinary Optimization, 2002, 23(3):189-203 doi: 10.1007/s00158-002-0177-3 [11] Evgrafov A. On globally stable singular truss topologies[J]. Structural and Multidisciplinary Optimization, 2005, 29(3):170-177 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=c6c5b7ab693e22e84b64d612b6712a7a [12] Guo X, Cheng G D, Olhoff N. Optimum design of truss topology under buckling constraints[J]. Structural and Multidisciplinary Optimization, 2005, 30(3):169-180 http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0210421491/ [13] Tyas A, Gilbert M, Pritchard T. Practical plastic layout optimization of trusses incorporating stability considerations[J]. Computers & Structures, 2006, 84(3-4):115-126 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a60b72ac319ba304c576c9e20bbf70e0 [14] Jalalpour M, Igusa T, Guest J K. Optimal design of trusses with geometric imperfections:accounting for global instability[J]. International Journal of Solids and Structures, 2011, 48(21):3011-3019 doi: 10.1016/j.ijsolstr.2011.06.020 [15] Van Den Boom S J. Topology optimisation including buckling analysis[D]. Delft, Netherlands: Delft University of Technology, 2014 https://repository.tudelft.nl/islandora/object/uuid%3Aa869dbe4-0280-4443-afb7-a3a386e3824b [16] 袁茹, 王三民, 谷文韬.卫星天线臂结构优化设计的分级遗传算法[J].机械科学与技术, 2007, 26(7):867-870 doi: 10.3321/j.issn:1003-8728.2007.07.010Yuan R, Wang S M, Gu W T. Optimal structure design of satellite antenna mast using hierarchical genetic algorithm[J]. Mechanical Science and Technology for Aerospace Engineering, 2007, 26(7):867-870(in Chinese) doi: 10.3321/j.issn:1003-8728.2007.07.010 [17] 王庆, 徐斌, 何佳琦.基于拓扑优化的结构动力学边界条件优化设计[J].机械科学与技术, 2012, 31(11):1845-1850 http://journals.nwpu.edu.cn/jxkxyjs/CN/abstract/abstract5495.shtmlWang Q, Xu B, He J Q. Optimal design of structural dynamic boundary conditions based on topology optimization method[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(11):1845-1850(in Chinese) http://journals.nwpu.edu.cn/jxkxyjs/CN/abstract/abstract5495.shtml [18] Li J P. Truss topology optimization using an improved species-conserving genetic algorithm[J]. Engineering Optimization, 2015, 47(1):107-128 http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0234180890/ [19] 董永芳, 黄海.桁架拓扑优化的多点逼近遗传算法[J].计算力学学报, 2004, 21(6):746-751 doi: 10.3969/j.issn.1007-4708.2004.06.020Dong Y F, Huang H. Truss topology optimization by using multi-point approximation and GA[J]. Chinese Journal of Computational Mechanics, 2004, 21(6):746-751(in Chinese) doi: 10.3969/j.issn.1007-4708.2004.06.020 [20] An H C, Huang H. Topology and sizing optimization for frame structures with a two-Level approximation method[J]. AIAA Journal, 2017, 55(3):1044-1057 doi: 10.2514/1.J055020 [21] 谢祚水, 王自力, 吴剑国.计算结构力学[M].武汉:华中科技大学出版社, 2004Xie Z S, Wang Z L, Wu J G. Computational structural mechanics[M]. Wuhan:Huazhong University of Science and Technology Press, 2004(in Chinese) [22] 咸奎成, 黄海.压电桁架作动器/传感器优化配置算法研究[J].计算力学学报, 2008, 25(6):827-832 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=SciencePaper201307170000413036Xian K C, Huang H. Research on algorithm of optimal actuator/sensor location for piezoelectric truss[J]. Chinese Journal of Computational Mechanics, 2008, 25(6):827-832(in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=SciencePaper201307170000413036 [23] Li D F, Chen S Y, Huang H. Improved genetic algorithm with two-level approximation for truss topology optimization[J]. Structural and Multidisciplinary Optimization, 2014, 49(5):795-814 http://dl.acm.org/citation.cfm?id=2617214 -







 下载:
下载: