Modeling and Simulation of Eel Robots in Non-inertial Frame
-
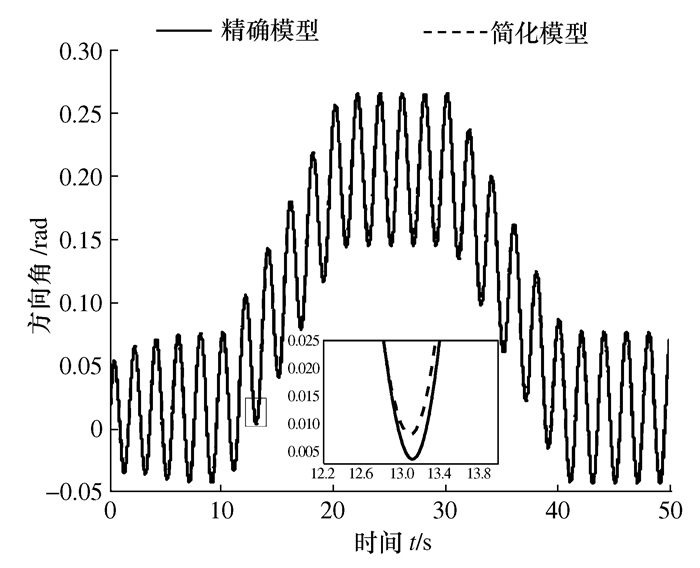
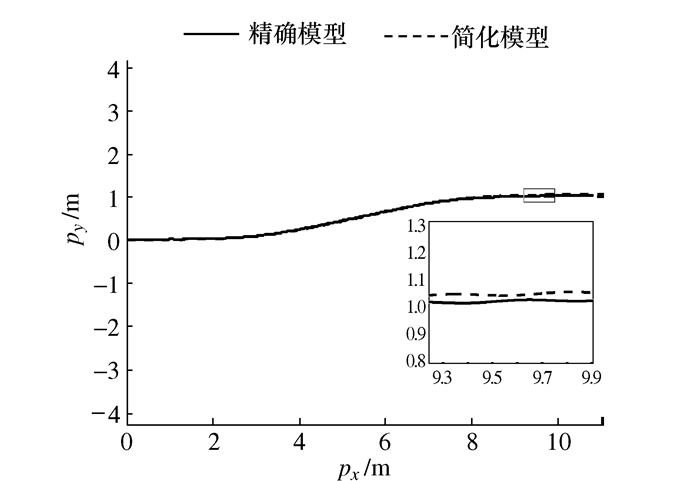
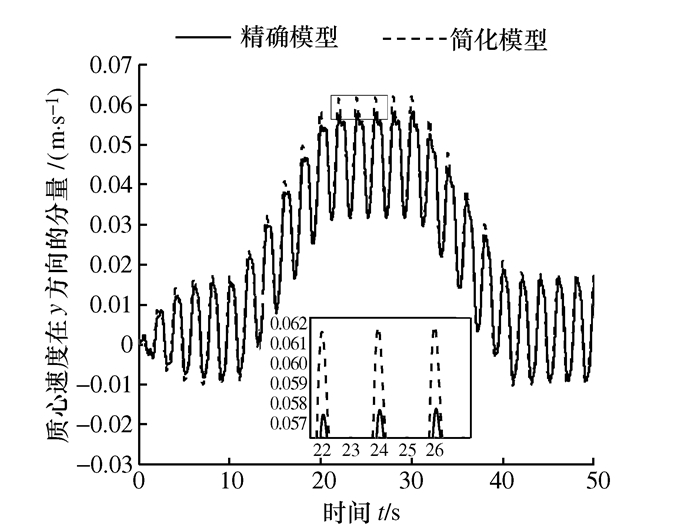
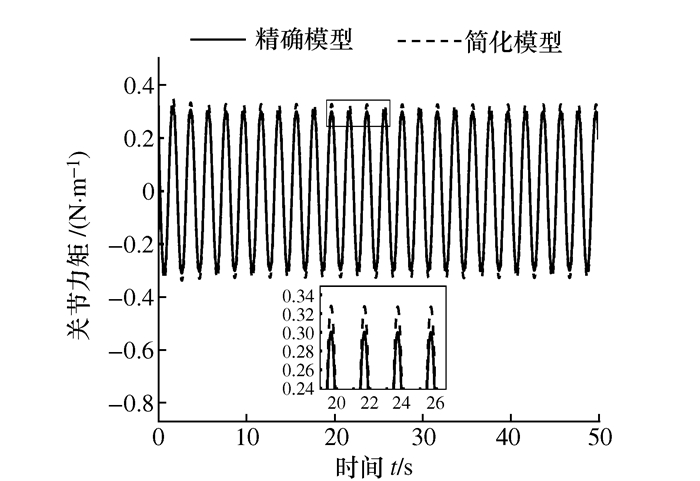
摘要: 在惯性系下得到的鳗鱼机器人的动力学方程由于耦合度高、非线性强而不利于控制器的设计。本文受自主水下航行器(AUV)基于体坐标系的模型表示法的启发,定义了一个与鳗鱼机器人运动方向一致的非惯性系。在该非惯性系下,利用科里奥利定理获得鳗鱼机器人的二维运动学模型,并利用改进的牛顿第二定律和力矩平衡原理获得水下二维鳗鱼机器人在非惯性系下的动力学模型。该模型是解析的,可直接获得切向速度子动力学,更适合于基于模型的现代控制方案,与精确模型相比,其通过方向角参数解耦实现了模型的简化。最后,对一个9模块的机器人系统进行了数值仿真,并与已有的精确模型进行了对比分析,发现所建立简化模型和精确模型的几乎重合,从而验证了所建立简化模型的准确性。Abstract: The existing dynamic equations in an inertial frame are highly coupled and fully nonlinear and therefore are not conducive to controller design. Inspired by autonomous underwater vehicle's (AUV) underwater modeling in non-inertia frame, this paper defines a non-inertial frame that is always aligned with the eel robot. This kinematics model is derived with the Coriolis theorem and are derived with the improved Newton's second law and the moment balance principle. The kinematics model is analytical and can obtain the tangent velocity sub-dynamics directly and be utilized in model-based modern control schemes. Compared with the existing model, the kinematics model established in this paper achieves the purpose of simplifying the model by decoupling orientation angle parameter. A nine-module robot is numerically simulated and the simulation results are compared with those of the existing exact model. It is found that the simplified model and the exact model almost coincide, thus verifying the accuracy of the simplified model.
-
Key words:
- eel-like robot /
- Newton-Euler modeling /
- non-inertial frame /
- kinematics model
-
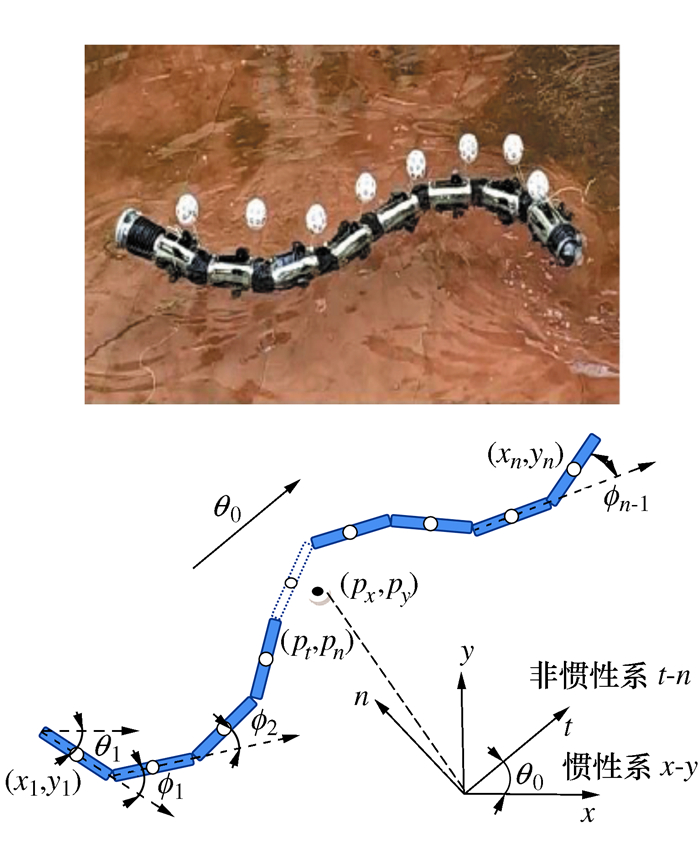
表 1 数学符号定义
变量 含义 n 模块数 l 单模块长度的一半 m 单位模块的质量 
机器人的方向角 J=ml2/3 每个模块的转动惯量 ϕ=[ϕ1, …, ϕn]T 关节角向量 θ=[θ1, …, θn]T 关于世界坐标系下的绝对角向量 Φ=[Φ1, …, Φn]T 关于非惯性系t-n的绝对角向量 (px, py)∈R2 质心在全局坐标系下表示 (pt, pn)∈R2 质心在非惯性系t-n下表示 -
[1] Crespi A, Badertscher A, Guignard A, et al. AmphiBot I:an amphibious snake-like robot[J]. Robotics and Autonomous Systems, 2005, 50(4):163-175 doi: 10.1016/j.robot.2004.09.015 [2] 郭宪.基于纤维丛理论的二维蛇形机器人建模与控制方法研究[D].沈阳: 中国科学院沈阳自动化研究所, 2015Guo X. Modeling and control of a planar snake-like robot based on the fiber bundle theory[D]. Shenyang: Shenyang Institute of Automation Chinese Academy of Sciences, 2015(in Chinese) [3] Ostrowski J, Burdick J, Lewis A D, et al. The mechanics of undulatory locomotion: the mixed kinematic and dynamic case[C]//Proceedings of 1995 IEEE International Conference on Robotics and Automation. Nagoya, Japan: IEEE, 1995, 1945-1951 [4] McIsaac K A, Ostrowski J P. A geometric approach to gait generation for eel-like locomotion[C]//Proceedings of 2000 IEEE/RSJ International Conference on Intelligent Robots and Systems. Takamatsu, Japan: IEEE, 2000: 2230-2235 [5] Liljebäck P, Pettersen K Y, Stavdahl O, et al. A simplified model of planar snake robot locomotion[C]//Proceedings of 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems. Taipei, Taiwan, China: IEEE, 2010: 2868-2875 [6] Tanaka M, Matsuno F. Experimental study of redundant snake robot based on kinematic model[C]//Proceedings of 2007 IEEE International Conference on Robotics and Automation. Roma, Italy: IEEE, 2007: 2990-2995 [7] Kelasidi E, Pettersen K Y, Gravdahl J T, et al. Modeling of underwater snake robots[C]//Proceedings of 2014 IEEE International Conference on Robotics and Automation. Hong Kong, China: IEEE, 2014: 4540-4547 [8] Khalil W, Gallot G, Ibrahim O, et al. Dynamic modeling of a 3-D serial eel-like robot[C]//Proceedings of 2005 IEEE International Conference on Robotics and Automation. Barcelona, Spain: IEEE, 2005: 1270-1275 [9] Khalil W, Gallot G, Boyer F. Dynamic modeling and simulation of a 3-D serial eel-like robot[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2007, 37(6):1259-1268 doi: 10.1109/TSMCC.2007.905831 [10] Melsaac K A, Ostrowski J P. A geometric approach to anguilliform locomotion: modelling of an underwater eel robot[C]//Proceedings of 1999 IEEE International Conference on Robotics and Automation. Detroit, MI, USA: IEEE, 1999: 2843-2848 [11] Chirikjian G S, Burdick J W. The kinematics of hyper-redundant robot locomotion[J]. IEEE Transactions on Robotics and Automation, 1995, 11(6):781-793 doi: 10.1109/70.478426 [12] Kelasidi E, Pettersen K Y, Gravdahl J T. A control-oriented model of underwater snake robots[C]//Proceedings of 2014 IEEE International Conference on Robotics and Biomimetics. Bali, Indonesia: IEEE, 2014: 753-760 [13] Kohl A M, Kelasidi E, Pettersen K Y, et al. A control-oriented model of underwater snake robots exposed to currents[C]//Proceedings of 2015 IEEE Conference on Control Applications. Sydney, NSW, Australia: IEEE, 2015: 1585-1592 [14] Kelasidi E, Pettersen K Y, Gravdahl J T. A waypoint guidance strategy for underwater snake robots[C]//Proceedings of the 22nd Mediterranean Conference on Control and Automation. Palermo, Italy: IEEE, 2014: 1512-1519 [15] Fossen T I. Guidance and control of ocean vehicles[M]. Norway:Wiley, 1994 [16] Taylor G. Analysis of the swimming of long and narrow animals[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1952, 214(1117):158-183 doi: 10.1098-rspa.1952.0159/ [17] Lighthill M J. Large-amplitude elongated-body theory of fish locomotion[J]. Proceedings of the Royal Society B:Biological Sciences, 1971, 179(1055):125-138 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=d9eb72e791213f9fe2a23d3eac492ae9 [18] Wiens A. Gait optimization for a multilink anguilliform swimmer[D]. Montreal: McGill University, 2013 -







 下载:
下载: