Analysis and Application of an Improved FFT Algorithm for Energy Centrobaric Correction Method
-
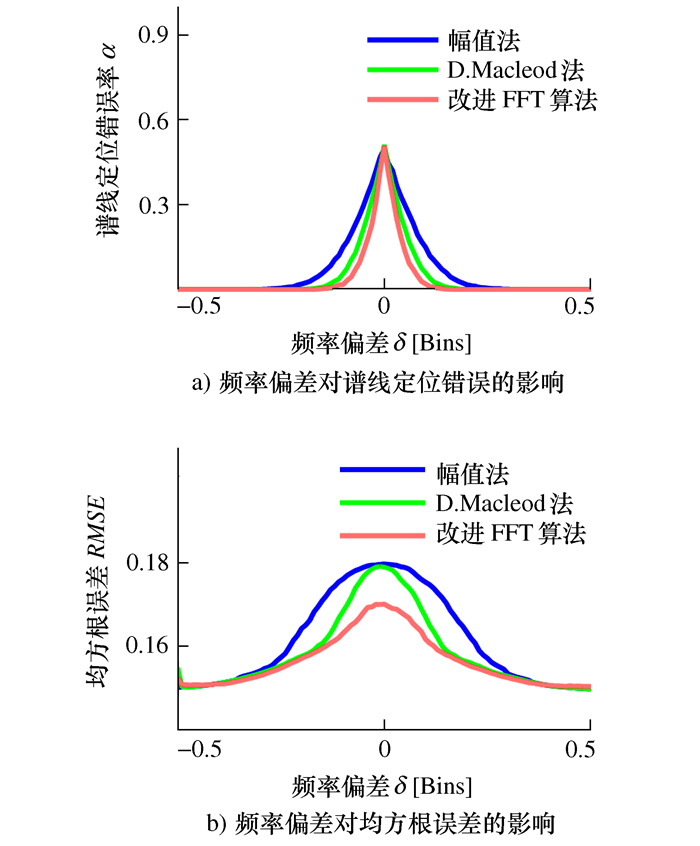
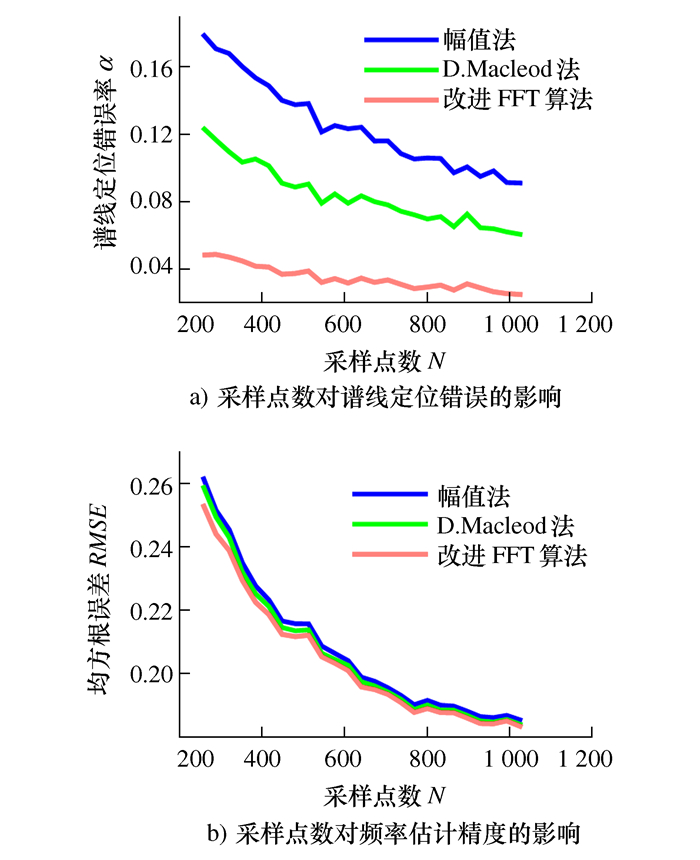
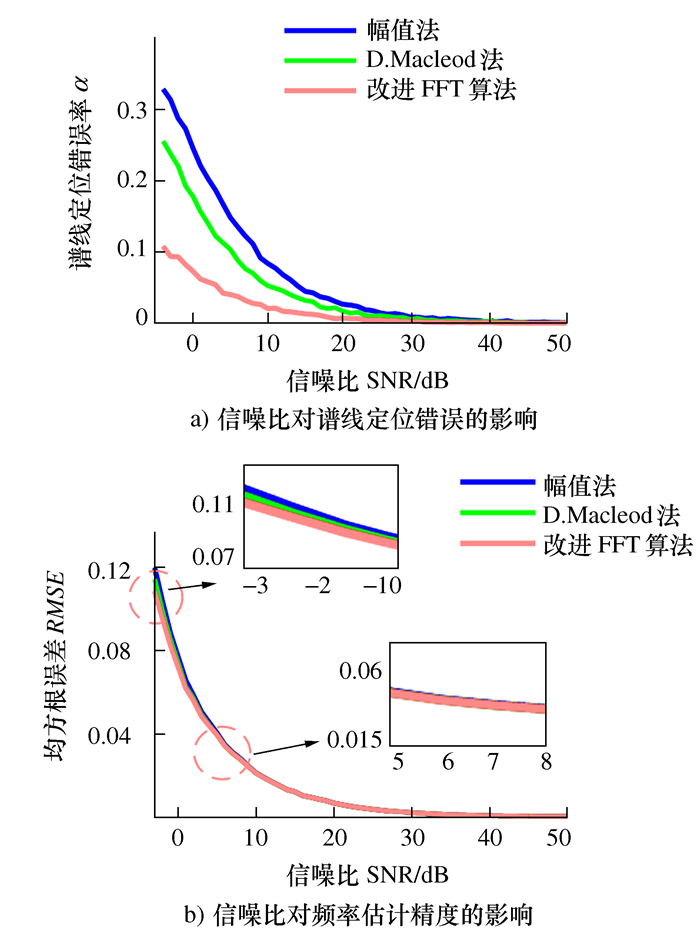
摘要: 研究噪声引起的谱线定位错误对能量重心法校正精度的影响。为了提高频率校正精度,在分析能量重心法理论和现有谱线选择方法的基础上,提出了一种减少谱线定位错误率的改进FFT校正算法。该算法在D.Macleod法基础上,利用谱线间的相位差确定谱线,减少了谱线定位错误。最后给出了通用的频率校正公式。仿真结果表明,改进算法谱线定位错误率低,抗噪性强,高斯白噪声条件下进行频率估计时较其他方法具有更小的均方根误差。在模拟井下套管的管道长度检测应用中进一步表明,改进方法具有更高的校正精度,有效地减少了长度测量误差。Abstract: The effect of wrong location of spectral bins caused by noise on frequency estimation was studied in the energy centrobaric correction method. In order to improve accuracy of frequency estimation, an improved FFT correction algorithm was proposed to decrease the ratio of wrong choices of spectral bins, based on the theory of the energy centrobaric correction method and existing methods for selecting spectral bins. The improved method, based on the D. Macleod method, selected the spectral bins by means of phase difference between the spectral lines, and reduced the occurrence of wrong location of spectral bins. Finally, a general formula of frequency correction was presented. The simulation results showed that the improved algorithm had a lower ratio of wrong choices of spectral bins and better anti-noise performance; And the method had a smaller root-mean-square error(RMSE) than the other methods when estimating the frequency in Gauss white noise. The application of pipeline length detection in the simulation of downhole casing further indicated that the improved method had higher frequency estimation accuracy and effectively decreased length measurement errors.
-
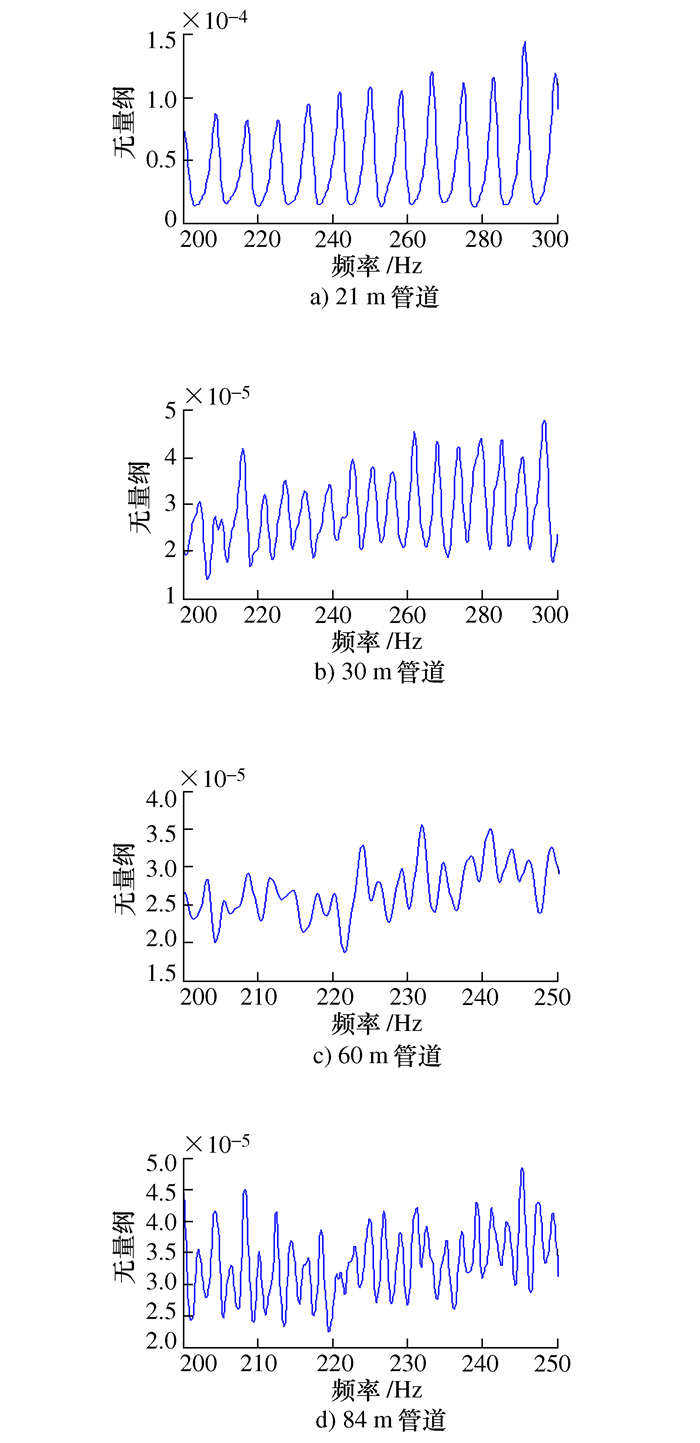
表 1 管道长度误差
m 管道长度 21 30 60 84 未校正 0.157 6 0.321 3 0.990 5 1.532 1 幅值法 0.125 9 0.257 3 0.782 1 1.232 8 D.Macleod法 0.079 11 0.162 5 0.502 7 0.777 3 改进算法 0.046 13 0.101 6 0.316 1 0.505 2 -
[1] Harris F J. On the use of windows for harmonic analysis with the discrete Fourier transform[J]. Proceedings of the IEEE, 1978, 66(1):51-83 doi: 10.1109/PROC.1978.10837 [2] Agrez D. Weighted multipoint interpolated DFT to improve amplitude estimation of multifrequency signal[J]. IEEE Transactions on Instrumentation and Measurement, 2002, 51(2):287-292 doi: 10.1109/19.997826 [3] Belega D, Dallet D. Multifrequency signal analysis by interpolated DFT method with maximum sidelobe decay windows[J]. Measurement, 2009, 42(3):420-426 doi: 10.1016/j.measurement.2008.08.006 [4] Kang D, Ming X, Xiaofei Z. Phase difference correction method for phase and frequency in spectral analysis[J]. Mechanical Systems and Signal Processing, 2000, 14(5):835-843 doi: 10.1006/mssp.1999.1284 [5] Mcmahon D R A, Barrett R F. An efficient method for the estimation of the frequency of a single tone in noise from the phases of discrete Fourier transforms[J]. Signal Processing, 1986, 11(2):169-177 doi: 10.1016/0165-1684(86)90035-6 [6] 丁康, 郑春松, 杨志坚.离散频谱能量重心法频率校正精度分析及改进[J].机械工程学报, 2010, 46(5):43-48 http://d.old.wanfangdata.com.cn/Periodical/jxgcxb201005007Ding K, Zheng C S, Yang Z J. Frequency estimation accuracy analysis and improvement of energy barycenter correction method for discrete spectrum[J]. Journal of Mechanical Engineering, 2010, 46(5):43-48(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/jxgcxb201005007 [7] 丁康, 江利旗.离散频谱的能量重心校正法[J].振动工程学报, 2001, 14(3):354-358 doi: 10.3969/j.issn.1004-4523.2001.03.022Ding K, Jiang L Q. Energy centrobaric correction method for discrete spectrum[J]. Journal of Vibration Engineering, 2001, 14(3):354-358(in Chinese) doi: 10.3969/j.issn.1004-4523.2001.03.022 [8] 丁康, 谢明.离散频谱三点卷积幅值修正法的误差分析[J].振动工程学报, 1996, 9(1):92-98 http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199600636753Ding K, Xie M. Error analysis for amplitude correction method using convolution of three points in discrete spectrum[J]. Journal of Vibration Engineering, 1996, 9(1):92-98(in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199600636753 [9] Grandke T. Interpolation algorithms for discrete Fourier transforms of weighted signals[J]. IEEE Transactions on Instrumentation and Measurement, 1983, 32(2):350-355 doi: 10.1109/TIM.1983.4315077 [10] 黄云志, 徐科军.基于相位差的频谱校正方法的研究[J].振动与冲击, 2005, 24(2):77-79, 86 doi: 10.3969/j.issn.1000-3835.2005.02.020Huang Y Z, Xu K J. Study on the spectrum correcting method based on phase difference[J]. Journal of Vibration and Shock, 2005, 24(2):77-79, 86(in Chinese) doi: 10.3969/j.issn.1000-3835.2005.02.020 [11] 林慧斌, 丁康.离散频谱四点能量重心校正法及抗噪性能分析[J].振动工程学报, 2009, 22(6):659-664 doi: 10.3969/j.issn.1004-4523.2009.06.017Lin H B, Ding K. Anti-noise performance of energy centrobaric correction method using four points for discrete spectrum[J]. Journal of Vibration Engineering, 2009, 22(6):659-664(in Chinese) doi: 10.3969/j.issn.1004-4523.2009.06.017 [12] Macleod M D. Fast nearly ML estimation of the parameters of real or complex single tones or resolved multiple tones[J]. IEEE Transactions on Signal Processing, 1998, 46(1):141-148 doi: 10.1109/78.651200 [13] Nuttall A. Some windows with very good sidelobe behavior[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1981, 29(1):84-91 doi: 10.1109/TASSP.1981.1163506 [14] Huang D S. Phase error in fast Fourier transform analysis[J]. Mechanical Systems and Signal Processing, 1995, 9(2):113-118 doi: 10.1006/mssp.1995.0009 [15] 周伟, 贾威, 郭小渝, 等.基于管柱声场模型的油井动液面检测新方法[J].西南石油大学学报(自然科学版), 2015, 37(4):166-172 http://d.old.wanfangdata.com.cn/Periodical/xnsyxyxb201504022Zhou W, Jia W, Guo X Y, et al. A new method for oil well dynamic fluid level detection based on the column sound field model[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(4):166-172(in Chinese) http://d.old.wanfangdata.com.cn/Periodical/xnsyxyxb201504022 -







 下载:
下载: