随着近年来环保问题日益受到人们的重视, 对民用航空发动机排放要求也越来越严苛。为此, 西北工业大学燃烧技术研究所提出了一种双旋流分区直混燃烧室方案[1], 采用直混燃烧可以有效避免预混燃烧遇到的回火与自燃问题。在副模燃烧区内通过化学恰当比燃烧方式可以获得良好的火焰稳定特性, 在整个燃烧区内通过贫油燃烧方式可以降低NOx排放[2-4]。在燃烧室内的非定常流场结构中, 能够维持某种特定运动状态的通常被称为相干结构。进动涡核(PVC)作为一种典型的大尺度相干结构, 经常出现在旋流稳定燃烧室内, 对燃烧室的流动特性和火焰稳定特性产生重要影响。
针对单旋流模型燃烧室, 当旋流数大于0.45时, 就可以在射流剪切层和回流区之间观察到明显的PVC现象[5-7]。PVC与燃烧室内部压力和速度的频谱图峰值之间存在强烈的内在联系[8]。PVC的最大强度通常出现在中心回流区的根部位置, 与中心回流区的相互作用能够促使其向燃烧室进口方向膨胀[9]。在一些研究中能同时观察到PVC的单螺旋和双螺旋空间结构[10]。当PVC存在时, 可以有效地提升燃料和空气的掺混作用, 增强火焰稳定能力[11]。燃烧室内的PVC会受到多种因素的影响, 其中旋流数可以通过改变涡破碎泡(VBB)的稳定性来影响PVC的形成过程[5]。此外, 受限空间的大小与形状[12]、边界条件(进口温度、压力和流量等)[13]以及燃烧释热[14]均会对PVC的空间结构和特征频率产生影响。
本征正交分解(POD)是一种数据驱动的线性降维方法, 在其他领域也被称为主成分分解(PCA)。Lumley首次将POD方法应用于流场相干结构的分析中[15], 利用一系列正交的基向量, 即空间模态, 来表征原始流场数据。随后, 因POD与流场分析优异的适配性以及低廉的计算成本, 有更多人利用它来捕捉旋流稳定燃烧室内的PVC结构[6]。
目前, 已开展了大量针对双旋流直混燃烧室稳态流场特性的数值模拟与试验工作, 但仍缺少对其非定常流动特性的深入研究。为此, 本文利用大涡模拟方法研究了双旋流直混燃烧室内的大尺度相干结构以及副模旋流器叶片角变化对其的影响规律。首先通过M准则对数值计算网格尺度进行检验, 并利用稳态PIV试验结果对数值方法进行验证。然后通过POD方法提取流场内的大尺度相干结构, 获得各相干结构对非定常流场特征的能量贡献比例, 通过对时间项的离散傅里叶变换(DFT)获得不同相干结构的频谱特性。最后研究了旋流器叶片角度变化对大尺度相干结构在空间和频域上的影响规律。
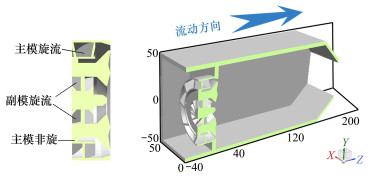
1 计算模型与数值方法 1.1 计算模型图 1为双旋流分区直混燃烧室和头部旋流器的剖视图。燃烧室由副模旋流器、主模旋流器和火焰筒三部分组成。其中副模旋流器叶片角度分别为35°、40°和45°, 叶片个数均为12。主模旋流器叶片角度为60°, 叶片个数为9。进入主模的气流被分成两部分, 一部分进入旋流器, 另一部分则由内侧的非旋通道流过, 两股气流合并后共同从主模出口喷射进入火焰筒内。火焰筒是一个50 mm×50 mm×185 mm的立方体, 在燃烧室出口设置有一个收敛段, 收敛角度为45°。
|
| 图 1 双旋流分区直混燃烧室计算模型 |
在开展数值模拟计算时, 燃烧室进口设定为质量流量入口, 燃烧室出口设定为压力出口。总的空气流量为0.066 kg/s, 各部件的空气流量则由设计时的流量分配比例决定。进口温度与压力分别为303 K和101 325 Pa。
1.2 数值方法本文中利用大涡模拟方法准确捕捉燃烧室内部的非定常流场结构。选用低速不可压缩求解器,利用SIMPLE方法实现压力和速度的耦合,分别通过二阶迎风方法和有界二阶隐式时间积分方法完成空间和时间的离散。利用Boussinesq假设处理控制方程中的应力项。滤波后的质量守恒和动量守恒方程分别如(1)~(2)式所示
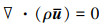
|
(1) |
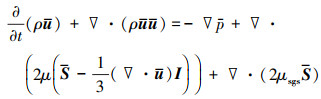
|
(2) |
式中:ρ为密度;u为滤波后的速度;p是滤波后的压力;S是应变率;I是3×3单位矩阵。利用Smagorinsky模型求解亚格子尺度涡粘性
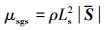
|
(3) |
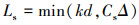
|
(4) |
式中:von Kármán常数k=0.41;d代表离最近壁面的距离;Smagorinsky常数Cs=0.1, Δ是局部网格尺寸。
1.3 POD方法用于POD分析的原始数据矩阵H[m, n], 是通过监测并记录燃烧室内不同时刻的流场信息而获得的。其中向量m和向量n的维度分别由监测点个数和快照数量决定。矩阵H可以表示为时均矩阵和瞬态矩阵之和
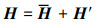
|
(5) |
其中, 时均矩阵也被称为0阶模态。鉴于本文分析关注的重点在大尺度相干结构上, 在进行POD分解前, 从原始数据中剔除了时均值。从数学角度来看, 去除时均矩阵的过程也是矩阵中心化的过程, 可以有效提升向量的正交性。对于中心化后的矩阵A, 其协方差矩阵R可由(7)式计算得到
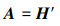
|
(6) |
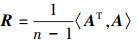
|
(7) |
对矩阵R进行本征正交分解以获得特征根矩阵, 也即空间模态。空间模态所对应的能量由特征值矩阵对角线上元素大小决定。
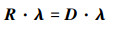
|
(8) |
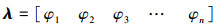
|
(9) |
式中:D是特征值矩阵;λ是特征根矩阵。时间项An由(10)式计算

|
(10) |
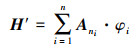
|
(11) |
根据(11)式, 瞬态矩阵可以表示为时间项和空间模态内积的累加。
2 计算结果分析 2.1 数值模拟方法验证Pope[16]提出的M准则可以用于检验网格捕捉湍动能的能力, 计算方法如(12)式所示
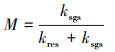
|
(12) |
式中:kres代表该网格尺度下可以直接求解的湍动能;ksgs代表未被直接求解, 需要用亚格子模型模拟的湍动能。当M数值小于0.2时, 表明该网格尺度下能够直接解析足够多的涡结构, 符合大涡模拟计算要求。
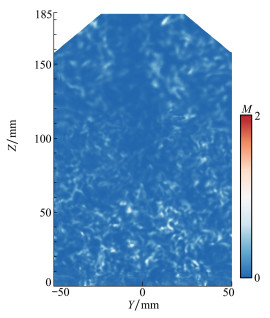
图 2中展示了燃烧室YZ截面内的M数值分布。经过多轮迭代, 当网格总数量为1 400万时, 可以看出燃烧室内M数值均小于0.2, 表明网格能够满足大涡模拟的计算要求。
|
| 图 2 燃烧室YZ截面M云图 |
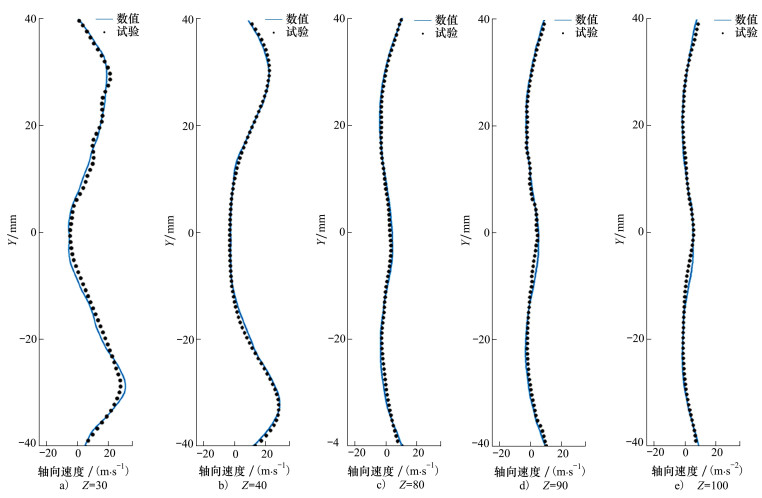
为了进一步证明数值计算结果的准确性, 对比了数值模拟与PIV试验在燃烧室多个轴向位置处的时均轴向速度沿径向的分布曲线,如图 3所示。
|
| 图 3 多个轴向位置的时均轴向速度径向分布对比 |
图 3中蓝色实线为数值仿真结果, 黑色圆点为PIV试验结果。从图中可以看出, 大涡模拟得到的时均轴向速度与PIV试验结果的趋势一致, 仅在数值上有细微差距, 表明数值计算结果是准确可靠的。
2.2 燃烧室内典型相干结构为了捕捉双旋流直混燃烧室内的大尺度相干结构, 共采集2 000组不同时刻的流场空间数据, 采样间隔为0.05 ms, 采样持续时间为0.1 s, 再利用1.3节介绍的POD方法, 获得了三维空间模态及其对应能量贡献大小。能量贡献越大的模态越能代表流场的非定常特征, 因此将POD模态按照能量贡献进行了降序排列。本节中选取副模旋流器叶片角度40°, 对双旋流直混燃烧室内的典型相干结构及其频谱特性进行展示。
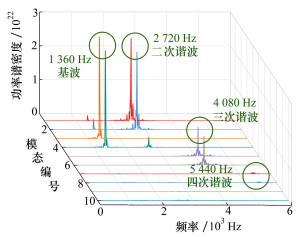
通过对POD分解得到的时间项An进行离散傅里叶变换, 可以获得不同模态的频谱特性曲线。图 4中展示了能量贡献最高的10个空间模态所对应的功率谱密度-频率特性曲线图。相邻的模态具有相同的特征频率, 而功率谱密度略有不同。其中, 前4组模态具有明显特征频率峰值, 分别是2 720, 1 360, 4 080和5 440 Hz。根据谐波的定义, 高次谐波的频率是基波的整数倍。因此, 模态3和模态4就共同表征了燃烧室内的基波结构, 其余特征频率对应的结构就分别为二次谐波结构, 三次谐波结构和四次谐波结构。相干结构对应的功率谱密度大小可以用来表征结构本身蕴含的能量高低。在现有标尺下, 第8模态后的频谱特性曲线中已经观察不到特征频率峰值, 表明这些相干结构蕴含的能量相比于基波结构的能量可以忽略不计。
|
| 图 4 前10模态的功率谱密度-频率特性曲线图 |
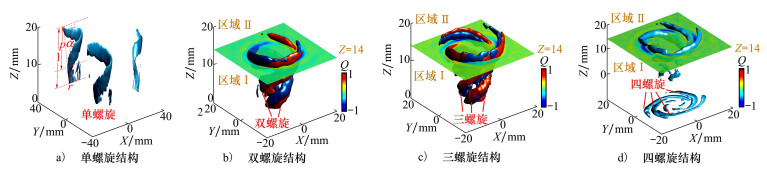
图 5中分别展示了基波和3种高次谐波所对应的三维空间结构, 图中的螺旋涡结构均通过Q等值面显示。相比于涡量等值面, 利用Q准则来表示流场内的涡量可以有效排除剪切流动带来的影响。
|
| 图 5 燃烧室内基波与3种高次谐波空间结构图 |
图 5a)表征了一种单螺旋涡结构, 从副模旋流器出口开始发展, 呈螺旋状向下游延伸。螺旋涡的外侧为副模旋转射流, 螺旋涡的内侧是回流区。螺旋运动的轴线为燃烧室的中轴线, 螺旋涡绕轴旋转的半径随着向下游发展逐渐增大。为了更好地表征螺旋涡的结构尺寸, 定义了几个结构参数, 分别是初始旋转半径r, 螺旋涡长度l, 螺距p, 以及螺旋扩张角α。图 5b)~5c)分别展示了双螺旋结构和三螺旋结构, 红色代表了模态1和模态5, 蓝色代表了模态2和模态6。以正弦曲线为例, 任何正弦曲线均能够分解为正弦分量和余弦分量的组合, 相位差为π/2。同理, 对于复杂的流场特征, 也需要用一对相位差为π/2的模态对其空间结构进行表征。这也印证了频谱特性曲线图中得到的结果。由于是单螺旋结构的高次谐波结构, 在保证涡结构完整的前提下, 双螺旋结构与三螺旋结构具有相同的初始半径r, 长度l, 螺距p和扩张角α。任意螺旋结构内相邻两支螺旋涡之间的相位差为2π/q, 其中q为空间结构所包含螺旋涡个数。图 5d)中展示了四次谐波所对应的空间结构, 由4支绕圆周均匀分布的螺旋涡组成。由图 4可知, 四螺旋结构的能量与其他3种螺旋结构相差一个数量级, 而含能越小的涡结构其尺度必然也随之减小, 无法维持完整的螺旋结构。因此从副模旋流器出口形成后就发生破碎, 直到下游才再次形成大尺度螺旋涡结构。
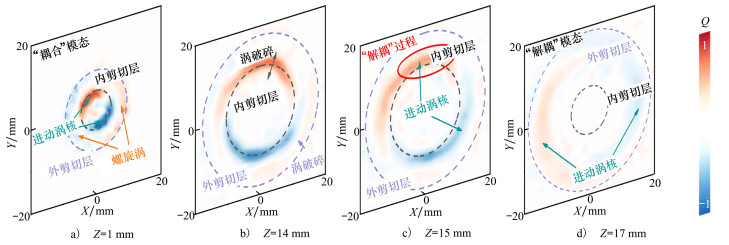
图 6中展示了剪切层和大尺度相干结构沿轴向的演变过程。图中内剪切层用灰色虚线标出, 外剪切层用紫色的虚线标出。涡量大小用归一化的Q来表征。通过图 6中Q分布云图, 能够发现2种大尺度相干结构。位于XY截面内侧的就是PVC, 而在截面外侧也能观察到一个强度弱于PVC的螺旋涡结构。内剪切层位于PVC中心, 由K-H不稳定性引起的剪切层边缘的涡脱落同时沿径向向内和向外发展; 外剪切层位于螺旋涡结构的外侧, 涡仅沿着径向向内脱落。在轴向位置小于14 mm的空间内, 内剪切层与PVC处于“耦合模态”, 螺旋涡包裹着剪切层, 剪切层能够持续地为PVC提供能量以维持其螺旋结构和进动状态。在旋流器出口下游15 mm位置处, 内剪切层与PVC发生“解耦”, 剪切层由螺旋涡中心变化到内侧边缘。
|
| 图 6 剪切层和大尺度相干结构沿轴向的演变过程 |
由图 6可知, 随着轴向距离的增加, 燃烧室内轴向速度的径向分布逐渐平缓, 轴向速度沿径向梯度逐渐降低, 剪切流强度随之减小。当剪切流内蕴含能量小于PVC内蕴含的能量, 产生“解耦”现象。当轴向位置为17 mm时, 将PVC与内剪切层完全分离的状态称为“解耦模态”。随着“解耦”的发生, 由于缺少了能量源, PVC能量随着涡破碎过程逐渐减小。利用开始发生解耦的轴向位置Z=14 mm截面将整个PVC结构分成2个部分, “发展区”和“耗散区”。“发展区”内大尺度涡结构能够维持完整的结构和进动模式, “耗散区”内的涡结构会在惯性作用下维持螺旋运动, 但由于缺少能量输入, 涡结构会逐渐破碎。对于由外剪切层涡脱落引起的位于内外剪切层之间的螺旋涡结构, 在Z=14 mm时就已经完全破碎, 主要原因是, 内外剪切层之间的湍流度要远大于内剪切层与回流区之间的湍流度。因此相比于PVC, 单螺旋涡结构更容易失去相干性。
当PVC与内剪切层处于“耦合模态”时, 可以利用内剪切层对PVC结构进行表征, 优点是易于获得准确的数值, 不受限与Q等值面的取值。因此, 在后续研究副模旋流器叶片角度对大尺度相干结构的影响规律时, 就利用剪切层代替PVC, 获得空间结构参数变化。
2.3 副模旋流器叶片角度对相干结构的影响副模旋流器叶片角度作为旋流器的关键参数之一, 会对副模旋流器出口处的流动特性产生重大影响。在本节中, 对不同副模旋流器叶片角度下的流场进行POD分析, 研究叶片角度对相干结构空间特征和频域特征的影响规律。其中空间特征定义在图 5a)中给出。
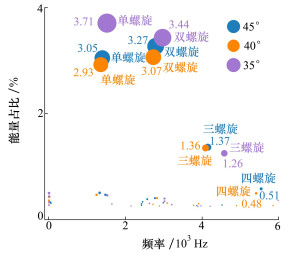
图 7中展示了3种叶片角度下, 不同相干结构对非稳态流场的能量贡献比例, 仅展示了能量占比前20的相干结构。蓝色, 橙色与紫色分别代表了3种叶片角度, 不同圆点代表了不同的相干结构, 非定常流场的能量贡献占比具体数值可以通过坐标轴读取, 而其相对大小可以根据圆点直径进行定性比较。图中标出了比较感兴趣的单螺旋结构及其各阶谐波结构的名称和能量贡献占比数值。
|
| 图 7 不同叶片角度各相干结构能量贡献比例图 |
总体来看, 能量贡献较高的相干结构均集中在5 000 Hz以内。能量贡献高的前提是相干结构本身蕴含有较大能量(PSD), 这也表明含能高的相干结构均分布在湍流能级串理论中的含能区内。叶片角为35°时, 单螺旋结构及其二次谐波和三次谐波占据了能量贡献的前三, 分别为3.71%, 3.44%和1.26%, 四次谐波模态能量贡献仅排第10位。
当叶片角从35°变为40°时, 基波与二次谐波的能量贡献均有明显降低, 基波从3.71%减小到2.93%, 二次谐波从3.44%减小到3.07%, 而其余高次谐波的能量占比都略有提高, 三螺旋结构从1.26%提升到1.36%, 四螺旋结构由能量贡献第10位提升到第4位, 0.48%。当叶片角从40°进一步增大到45°时, 基波及其谐波结构能量占比均进一步提高, 提高幅度按照能量贡献排序, 即二次谐波能量提高幅度最大, 基波能量提高幅度次之, 最终的能量贡献分别是3.05%, 3.27%, 1.37%和0.51%。二次谐波对流场结构的能量贡献要大于基波, 即双螺旋结构取代单螺旋结构, 在非定常流场中占据主导地位。
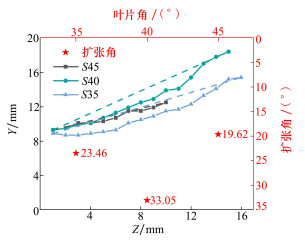
图 8展示了叶片角度对螺旋涡初始半径和扩张角的影响。
|
| 图 8 叶片角度对螺旋涡初始半径和扩张角的影响图 |
由上文分析可知, 剪切层在一定条件下会与螺旋涡“解耦”, 因此, 只统计了“耦合模态”下的剪切层空间位置信息, 用以代表螺旋涡的结构。在旋流器出口处, 受旋流流动所产生的离心力影响, 射流空气会沿径向向外侧移动, 45°叶片产生的离心力最强, 螺旋涡的初始半径也就最大。3种叶片角度下, 单螺旋涡的初始半径分别为4.85, 4.44和2.83 mm。副模旋流器出口半径仅为9.1 mm, 螺旋涡越向壁面位置迁移, 受到的阻力也越大, 因此, 相比于叶片角度从35°变为40°时, 当叶片角度从40°变为45°时, 螺旋涡初始半径的变化要小很多。如图 8中虚线所示, 将剪切层沿轴向首尾相连并读取扩张角大小, 以红色星号展示在图中。随叶片角增大, 扩张角先增大后减小, 45°时扩张角最小为19.62°, 40°时扩张角最大为33.05°。螺旋涡或剪切层的扩张运动是由旋转射流的径向速度分量驱动的, 随着叶片角增大, 旋转射流的径向速度分量越大, 扩张角理应越大。但当叶片角度为45°时, 叶片角过大导致在叶背和旋流器轮毂背面均产生了流动分离, 旋流器内总压损失提高, 出口位置合速度减小。因此, 即便其旋流强度是3种叶片角度中最大的, 径向速度在合速度中占比最高, 但合速度本身降低最终导致其螺旋涡扩张角最小。
3 结论本文针对一种双旋流分区直混燃烧室, 利用大涡模拟方法, 研究了无反应条件下燃烧室内的大尺度相干结构及副模旋流器叶片角度变化(35°, 40°, 45°)对其的影响规律, 获得以下结论:
1) 在副模旋流器下游存在典型的单螺旋涡、双螺旋涡、三螺旋涡和四螺旋涡结构, 均由一对相位差为π/2的模态来共同表征。根据4种涡结构的特征频率判断, 单螺旋涡为非稳态流场内的基波模态, 其余涡结构均为单螺旋涡的高次谐波模态, 频率均为基波的整数倍。
2) 副模出口的大尺度相干结构, 来自于剪切射流引起的K-H不稳定性所导致的涡破碎, 螺旋形状来源于由旋流器引起的旋转射流。根据与剪切层的“解耦”位置, 将PVC在空间上分为2个区域, 分别是“发展区”和“耗散区”。
3) 在频域内, 随着副模旋流器叶片角度增大, 大尺度相干结构对应的特征频率先减小, 后增大; 高次谐波对流动不稳定性的能量贡献逐渐提高; 二次谐波模态的双螺旋结构取代基波模态的单螺旋结构, 成为非定常流场内的主导结构。
4) 在空间内, 随着副模旋流器叶片角度增大, 螺旋涡结构的初始半径逐渐增大; 螺旋涡的扩张角先增大后减小; 剪切层与螺旋涡解耦的位置逐渐提前, 但螺旋涡总长度变化不明显。
| [1] |
于涵, 索建秦, 朱鹏飞, 等. 中心分级贫油直喷(LDI)燃烧室流动及污染排放特性研究[J]. 西北工业大学学报, 2018, 36(5): 816-823.
YU Han, SUO Jianqin, ZHU Pengfei, et al. The characteristic of flow field and emissions of a concentric staged lean direct injection(LDI) combustor[J]. Journal of Northwestern Polytechnical University, 2018, 36(5): 816-823. (in Chinese) |
| [2] |
于涵, 索建秦, 郑龙席. 带收敛出口的单元贫油直喷燃烧室冷态和热态流动特性研究[J]. 推进技术, 2019, 40(3): 608-618.
YU Han, SUO Jianqin, ZHENG Longxi. Investigation of non-reaction and reaction flow characteristic of single element lean direct injection combustor with convergent outlet[J]. Journal of Propulsion Technology, 2019, 40(3): 608-618. (in Chinese) |
| [3] |
李乐, 索建秦, 郑龙席. 旋向对中心分级燃烧室流场及温度场影响研究[J]. 西北工业大学学报, 2020, 38(6): 1198-1209.
LI Le, SUO Jianqin, ZHENG Longxi. Effect of rotating direction on flow and temperature field of concentric staged combustor[J]. Journal of Northwestern Polytechnical University, 2020, 38(6): 1198-1209. (in Chinese) |
| [4] |
李乐, 索建秦, 于涵, 等. 中心分级多点直喷燃烧室冷态流动特性研究[J]. 推进技术, 2021, 42(6): 1339-1350.
LI Le, SUO Jianqin, YU Han, et al. Non-reaction flow characteristic of concentric staged multi-point direct injection combustor[J]. Journal of Propulsion Technology, 2021, 42(6): 1339-1350. (in Chinese) |
| [5] | DUROX D, MOECK J P, BOURGOUIN J F, et al. Flame dynamics of a variable swirl number system and instability control[J]. Combustion and Flame, 2013, 160(9): 1729-1742. DOI:10.1016/j.combustflame.2013.03.004 |
| [6] | SALVADOR F J, CARRERES M, GARCIA-TISCAR J, et al. Modal decomposition of the unsteady non-reactive flow field in a swirl-stabilized combustor operated by a Lean Premixed injection system[J]. Aerospace Scinence and Technology, 2021, 112: 106622. DOI:10.1016/j.ast.2021.106622 |
| [7] | LUCCA-NEGRO O, O'DOHERTY T. Vortex breakdown: a review[J]. Progress in Energy and Combustion Science, 2001, 27(4): 431-481. DOI:10.1016/S0360-1285(00)00022-8 |
| [8] | VASHAHI F, LEE J. On the emerging flow from a dual-axial counter-rotating swirler: LES simulation and spectral transition[J]. Applied Thermal Engineering, 2018, 129: 646-656. DOI:10.1016/j.applthermaleng.2017.10.058 |
| [9] | RANGA DINESH K K J, KIRKPATRICK M P, JENKINS K W. Investigation of the influence of swirl on a confined coannular swirl jet[J]. Computers & Fluids, 2010, 39(5): 756-767. |
| [10] | VALERA-MEDINA A, SYRED N, GRIFFITHS A. Visualisation of isothermal large coherent structures in a swirl burner[J]. Combustion and Flame, 2009, 156(9): 1723-1734. |
| [11] | GOMEZ-RAMIREZ D, EKKAD S V, MOON H K, et al. Isothermal coherent structures and turbulent flow produced by a gas turbine combustor lean pre-mixed swirl fuel nozzle[J]. Experimental Thermal and Fluid Science, 2017, 81: 187-201. |
| [12] | SYRED N. A review of oscillation mechanisms and the role of the precessing vortex core (PVC) in swirl combustion systems[J]. Progress in Energy and Combustion Science, 2006, 32(2): 93-161. |
| [13] | HUANG D X, XU J G, CHEN R Y, et al. Large eddy simulations of turbulent combustion of kerosene-air in a dual swirl gas turbine model combustor at high pressures[J]. Fuel, 2020, 282: 118820. |
| [14] | CLAYPOLE T C, SYRED N. Coherent structures in swirl generators and combustors[C]//Proceedings of the ASME Symposium Vortex Flows, Winter Annual Meeting, Chicago, 1980 |
| [15] | LUMLEY J L. The structure of inhomogeneous turbulence flows[C]//Atmospheric Turbulence and Radio Wave Propagation, Moscow: Nauka, 1967: 166-178 |
| [16] | POPE S B. Ten questions concerning the large-eddy simulation of turbulent flows[J]. New Journal of Physics, 2004, 6: 35. |




