2. 西北工业大学 力学与土木建筑学院, 陕西 西安 710072
随着材料科学的发展, 具有多物理场耦合特性的电磁弹性复合材料已经广泛用于智能器件的开发与制造中[1-2]。该类材料往往由两相或多相压电和压磁材料按照一定的方式复合而成。由于不同材料相间的失配性, 电磁弹性复合材料在制造和使用过程中会不可避免地出现界面裂纹。这些裂纹会在外荷载作用下产生应力集中, 进而引发结构失效破坏, 造成安全事故。因此, 研究电磁弹性复合材料的界面断裂问题具有重要的理论和实际意义。
在现有研究中, 解析方法往往仅限于求解无限大或半无限大电磁弹性材料中的裂纹问题, 如积分方程方法[3]、Stroh变换方法[4]。对于有限几何尺寸的含裂纹电磁弹性材料还主要依赖于数值方法, 如有限元方法[5]、边界元法[6]和无网格方法[7]。然而, 大部分数值方法仅适用于单相电磁弹性材料, 无法直接应用于双相电磁弹性复合材料的界面断裂分析。为解决上述问题, 本文提出一种适用于电磁弹性复合材料反平面界面断裂分析的辛离散有限元方法。该方法将一类基于哈密顿体系的解析方法[8]与传统有限元方法相结合, 能够简单、高效地获得相关断裂参数, 并同时获得裂纹尖端附近奇异物理场的显式表达式。目前, 该方法已经成功应用于弹性材料与压电材料的断裂分析中[9]。
本文提出的辛离散有限元方法可以分为2步:第一, 根据裂纹尖端的位置将整体结构分为2类区域, 即包含奇异性的近场和无奇异性的远场;第二, 通过在裂纹尖端附近引入解析的辛本征解函数, 实现该区域内的未知量变换, 将数量庞大的节点未知量转化为少量的辛本征解待定系数。该方法可以避免传统有限元方法在计算断裂参数时的网格敏感性和路径依赖性, 直接提高计算效率和计算精度。
1 电磁弹性材料反平面有限元列式考虑如图 1所示的含界面裂纹的电磁弹性复合材料。上下层材料分别记为材料1(M1)和材料2(M2), z轴选取为电磁弹性介质的极化方向, 坐标原点位于裂纹尖端。结构承受反平面剪应力τ0, 平面内电位移D0和磁感应强度B0。曲线Γ0将整体结构划分为2类区域, 即近场区域和远场区域。
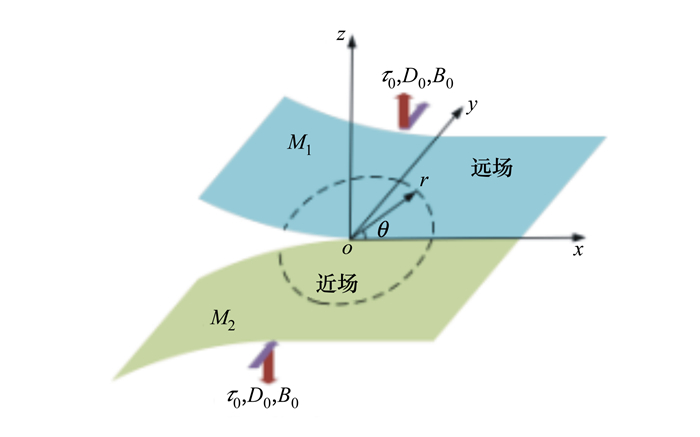
|
| 图 1 含裂纹电磁弹性复合结构 |
在直角坐标系下, 电磁弹性复合材料在反平面荷载作用下的基本方程可以表示为:
本构方程
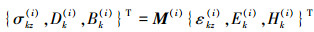
|
(1) |
几何方程
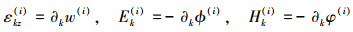
|
(2) |
平衡方程
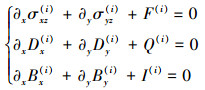
|
(3) |
式中,w(i), ϕ(i)和φ(i)分别为反平面位移、电势和磁势; σk(i), Dk(i)和Bk(i)是应力、电位移和磁感应强度分量; εkz(i), Ek(i)和Hk(i)是应变、电场强度和磁场强度分量; C44(i), e15(i), h15(i), g11(i)为弹性、压电、压磁和电磁耦合常数; κ11(i), χ11(i)为介电常数和磁通率; F(i), Q(i)和I(i)是体力、点电荷和电流密度; k=x, y, 上标i表示材料区域编号, M(i)为材料常数矩阵, 见附录(A-1)。
本文使用的电磁弹性材料单元为八节点四边形单元。单元内任意点未知量由节点未知量表示
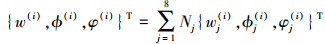
|
(4) |
式中,Nj是形函数。单元势能可以表示为
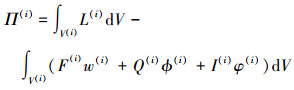
|
(5) |
式中,L(i)为应变能密度函数
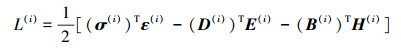
|
(6) |
式中,σ(i)={σxz(i), σyz(i)}T, D(i)={Dx(i), Dy(i)}T, B(i)={Bx(i), By(i)}T, ε(i)={εxz(i), εyz(i)}T, E(i)={-Ex(i), -Ey(i)}T, H(i)={-Hx(i), -Hy(i)}T。
将(1)式、(2)式和(4)式带入(5)式可得
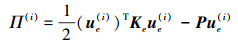
|
(7) |
式中,P为等效节点载荷; ue(i)为单元节点位移向量ue(i)={w1(i), …, w8(i), ϕ1(i), …, ϕ8(i), φ1(i), …, φ8(i)}T。
根据最小势能原理δΠ(i)=0, 可得
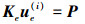
|
(8) |
式中,Ke是单元刚度矩阵。根据节点编号, 组集整体刚度矩阵、节点位移向量和整体载荷向量, 可得电磁反平面有限元列式为
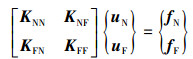
|
(9) |
式中,K为刚度矩阵, f为荷载向量, 下标N和F分别代表近场和远场区域。
2 电磁弹性材料Ⅲ型界面断裂辛方法在近场区域, 定义全状态向量为
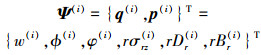
|
(10) |
则电磁弹性复合材料Ⅲ型界面断裂问题的哈密顿控制方程可以表示为
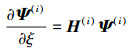
|
(11) |
式中,H(i)为哈密顿矩阵, 见附录(A-2)。界面连续条件为
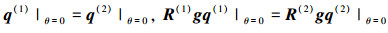
|
(12) |
裂纹面边界条件为
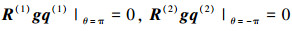
|
(13) |
式中,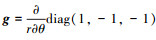
利用分离变量法求解哈密顿方程(11), 并结合(12)式和(13)式得到问题的辛本征值和本征解, 见附录(A-3~A-7)。因此, 双材料电磁反平面的位移, 电势和磁势可以表示为
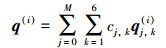
|
(14) |
式中,M是所取的本征解项数, cj, k为待定系数。
3 辛离散有限元方法由(14)式, 近场区域内节点未知量可以表示为
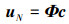
|
(15) |
式中,c={c0, 1, c0, 2, c0, 3, c1, 1, …, c1, 6, c2, 1, …, cM, 6}T为辛展开函数的待定系数向量
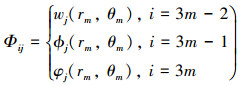
|
(m=1, 2, …, NΩN; j=1, 2, …, 3M+6), NΩN为近场区域内总节点数, (rm, θm)是第m个节点的极坐标。将(15)式代入(9)式, 则电磁反平面断裂问题的辛离散有限元表达式为
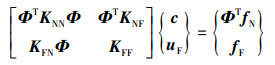
|
(16) |
由(1)式和辛本征解可知, 在裂纹尖端(r=0)[10], 广义应力强度因子可以表示为
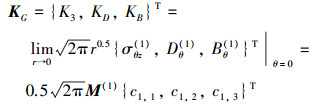
|
(17) |
式中, K3, KD和KB分别为应力强度因子、电位移强度因子和磁感应强度因子, 是由反平面剪应力τ0, 平面内电位移D0和磁感应强度B0耦合作用的结果。能量释放率为
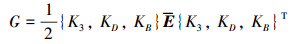
|
(18) |
式中,E=[(R(1))-1+(R(2))-1]/2。
5 数值算例为验证本文提出方法的正确性与有效性, 数值算例计算了3种典型裂纹对应的断裂参数。本节中所有计算数据均采用无量纲形式[10], 涉及的材料参数如表 1所示。
| 材料 | C44/ (N·m-2) | e15/ (C·m-2) | h15/ (N·(m·A)-1) | κ11/ (F·m-1) | g11/ (Ns·(VC)-1) | χ11/ (Ns2·C-2) |
| M1 | 4.4×1010 | 5.8 | 275 | 5.64×10-9 | 5.367×10-8 | -2.97×10-4 |
| M2 | 3.4×1010 | 4.8 | 195 | 4.64×10-9 | 4×10-8 | -2.01×10-4 |
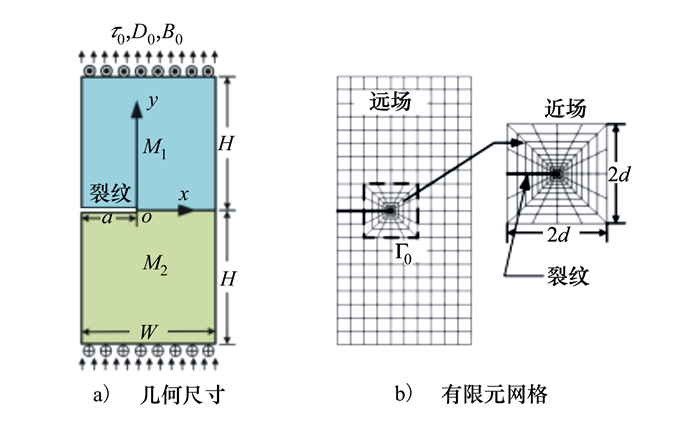
考虑1个受到均布荷载作用的含边裂纹电磁弹性材料矩形板, 其几何尺寸和有限元网格如图 2所示。取τ0=1, D0=1, B0=1, d=0.5a, M2=M1, 表 2给出了不同高度和宽度下各奇异物理场的强度因子和能量释放率。由于结构关于x轴对称, 故有K3*=KD*=KB*=K*[11]。从表中数据可以看出, 各强度因子与能量释放率均随高度和宽度的增加而减小, 并且逐渐趋近于稳定值, 即H→∞和W→∞对应的值[12-13]。当W/a=5时, 最大误差仅为1.15%。这表明本文方法具有良好的计算精度, 能够有效计算含裂纹电磁弹性材料的断裂参数。
|
| 图 2 含边裂纹电磁弹性矩阵板 |
| W/a | H/a | ||||||
| 0.5 | 1 | 2 | 3 | 4 | ∞[12] | ||
| 1.5 | K* | 1.411 1 | 1.295 8 | 1.282 0 | 1.281 8 | 1.281 8 | 1.286 1 |
| G | 1.561 4 | 1.316 6 | 1.288 7 | 1.288 3 | 1.288 3 | 1.296 9 | |
| 2 | K* | 1.390 8 | 1.172 0 | 1.126 3 | 1.124 3 | 1.124 2 | 1.128 4 |
| G | 1.503 5 | 1.077 1 | 0.994 6 | 0.991 2 | 0.991 1 | 0.998 3 | |
| 3 | K* | 1.387 9 | 1.157 9 | 1.058 8 | 1.050 1 | 1.048 8 | 1.050 1 |
| G | 1.498 7 | 1.053 3 | 0.879 0 | 0.864 6 | 0.862 5 | 0.864 6 | |
| 4 | K* | 1.383 5 | 1.151 2 | 1.051 4 | 1.030 7 | 1.026 7 | 1.027 0 |
| G | 1.490 7 | 1.047 3 | 0.869 2 | 0.833 0 | 0.826 5 | 0.827 1 | |
| 5 | K* | 1.377 9 | 1.150 4 | 1.049 9 | 1.025 0 | 1.018 3 | 1.017 0 |
| G | 1.488 1 | 1.039 4 | 0.864 4 | 0.823 9 | 0.813 1 | 0.810 9 | |
| ∞[13] | K* | 1.377 3 | 1.149 3 | 1.046 5 | 1.021 8 | 1.012 5 | 1.000 0 |
| G | 1.487 5 | 1.035 7 | 0.858 7 | 0.818 7 | 0.803 8 | 0.784 1 | |
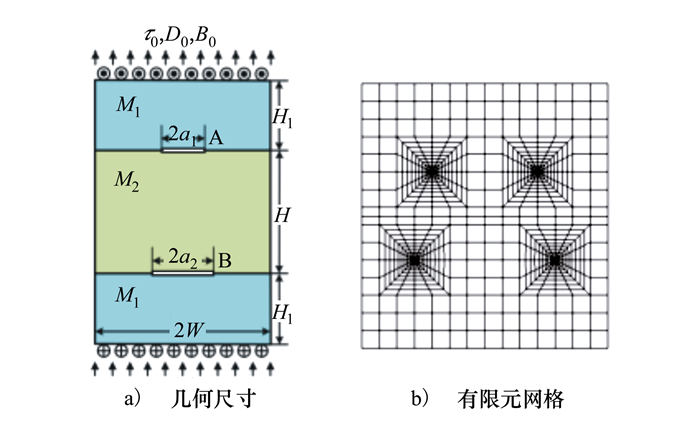
图 3为1个含有平行裂纹的电磁弹性材料矩形板, 其裂纹长度分别为2a1和2a2。该板两端受到均布荷载τ0=1, D0=1和B0=1作用。令W=1, H/W=0.5, H1/W=0.5, 表 3给出了不同裂纹长度对应的裂纹尖端A处的强度因子与能量释放率。从表中数据可以看出, 对于给定的a2, 各强度因子与能量释放率总是随着的a1增加而增大; 而对于给定的a1, 断裂参数表现出相反的变化趋势。表 4给出了裂纹长度相同时(a1=a2)断裂参数随H/W的变化规律。从表中可以看到, 各断裂参数随着H/W单调变化, 并逐渐趋近于某一固定值。该现象可以通过圣维南原理解释, 当H/W增加到一定值时, 边缘效应不再对裂纹尖端物理场分布产生影响。
|
| 图 3 含2条平行裂纹电磁矩阵板 |
| a2/W | a1/W | ||||||
| 0.2 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | ||
| 0.2 | K3* | 0.977 4 | 1.068 0 | 1.131 5 | 1.216 7 | 1.344 6 | 1.570 4 |
| KD* | 0.979 4 | 1.070 1 | 1.133 6 | 1.218 6 | 1.346 1 | 1.571 3 | |
| KB* | 1.055 4 | 1.148 6 | 1.210 9 | 1.288 8 | 1.401 6 | 1.606 3 | |
| G | 0.342 9 | 0.818 9 | 1.148 9 | 1.594 1 | 2.271 2 | 3.540 6 | |
| 0.5 | K3* | 0.810 2 | 0.946 1 | 1.040 7 | 1.155 9 | 1.308 6 | 1.552 6 |
| KD* | 0.817 1 | 0.951 4 | 1.044 9 | 1.159 1 | 1.310 8 | 1.553 9 | |
| KB* | 1.068 7 | 1.145 2 | 1.201 6 | 1.277 7 | 1.392 3 | 1.600 6 | |
| G | 0.235 7 | 0.642 6 | 0.971 9 | 1.438 7 | 2.151 2 | 3.460 9 | |
| 0.8 | K3* | 0.694 9 | 0.818 9 | 0.916 7 | 1.047 0 | 1.226 6 | 1.504 1 |
| KD* | 0.705 1 | 0.827 7 | 0.924 4 | 1.053 1 | 1.231 0 | 1.506 6 | |
| KB* | 1.076 9 | 1.151 3 | 1.204 9 | 1.277 5 | 1.389 6 | 1.597 5 | |
| G | 0.173 4 | 0.481 6 | 0.754 3 | 1.180 6 | 1.890 4 | 3.248 0 | |
| a1/W | H/W | ||||||
| 0.3 | 0.5 | 1 | 1.5 | 2 | 5 | ||
| 0.2 | K3* | 0.918 0 | 0.977 4 | 1.017 3 | 1.024 0 | 1.025 4 | 1.025 7 |
| KD* | 0.922 1 | 0.979 4 | 1.017 9 | 1.024 5 | 1.025 8 | 1.026 1 | |
| KB* | 1.073 6 | 1.055 4 | 1.041 3 | 1.039 6 | 1.039 3 | 1.039 2 | |
| G | 0.302 5 | 0.342 9 | 0.371 4 | 0.376 4 | 0.377 4 | 0.377 6 | |
| 0.5 | K3* | 0.969 0 | 1.040 7 | 1.122 6 | 1.142 9 | 1.147 3 | 1.148 5 |
| KD* | 0.975 8 | 1.044 9 | 1.124 2 | 1.143 9 | 1.148 1 | 1.149 2 | |
| KB* | 1.227 0 | 1.201 6 | 1.182 4 | 1.179 1 | 1.178 5 | 1.178 3 | |
| G | 0.842 8 | 0.971 9 | 1.130 9 | 1.172 1 | 1.181 1 | 1.183 5 | |
| 0.8 | K3* | 1.423 1 | 1.504 1 | 1.560 5 | 1.571 1 | 1.573 3 | 1.573 8 |
| KD* | 1.428 0 | 1.506 6 | 1.561 3 | 1.571 6 | 1.573 7 | 1.574 2 | |
| KB* | 1.607 4 | 1.597 5 | 1.590 5 | 1.589 2 | 1.589 0 | 1.588 9 | |
| G | 2.908 1 | 3.248 0 | 3.496 2 | 3.543 7 | 3.553 5 | 3.556 1 | |
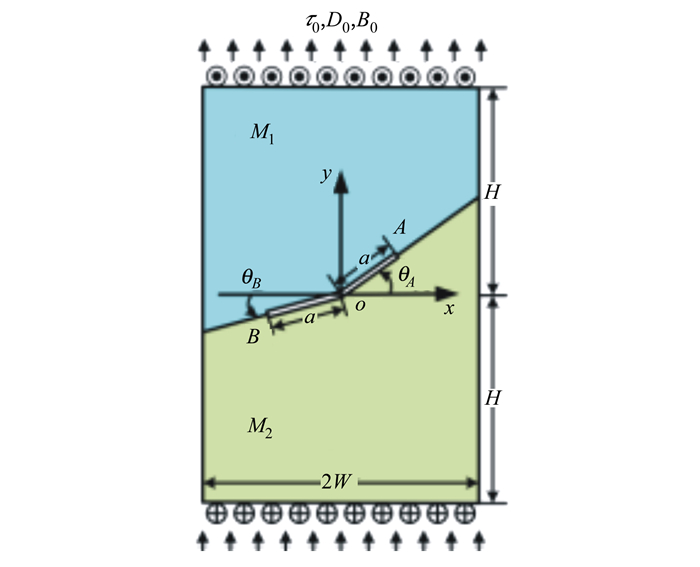
考虑如图 4所示的1个含有折线裂纹的电磁弹性材料矩形板。裂纹与水平方向的偏离角度分别为θA和θB。令W=H, a=0.4H, τ0=1, D0=1和B0=1, 表 5和表 6分别给出了的裂纹尖端A和B处的强度因子和能量释放率随θA和θB的变化规律。从表 5中可以看出, 所有断裂参数随θA的增大均表现出先增大后减小的趋势。当θA=0时, 应力、电位移强度因子和能量释放率达到最大值。表 6表现出与表 5相似的变化趋势。从上述现象可以看出, 合理控制外部电磁场可以有效改变电磁弹性材料裂纹尖端的能量释放率, 从而阻滞裂纹扩展。
|
| 图 4 含有折线裂纹电磁矩形板 |
| θB | θA | |||||
| -π/4 | -π/10 | 0 | π/10 | π/4 | ||
| -π/6 | K3* | 0.757 3 | 0.968 5 | 1.017 1 | 0.982 1 | 0.789 0 |
| KD* | 0.771 9 | 0.979 5 | 1.025 1 | 0.987 1 | 0.788 9 | |
| KB* | 1.301 4 | 1.383 7 | 1.323 8 | 1.171 8 | 0.781 7 | |
| G | 0.412 0 | 0.673 6 | 0.742 8 | 0.692 5 | 0.446 9 | |
| 0 | K3* | 0.798 2 | 1.019 5 | 1.073 6 | 1.043 0 | 0.855 3 |
| KD* | 0.805 4 | 1.022 6 | 1.073 6 | 1.039 9 | 0.847 4 | |
| KB* | 1.061 6 | 1.135 9 | 1.073 7 | 0.926 1 | 0.554 5 | |
| G | 0.457 5 | 0.746 1 | 0.827 4 | 0.780 8 | 0.524 9 | |
| π/6 | K3* | 0.788 7 | 1.017 9 | 1.076 8 | 1.050 8 | 0.869 8 |
| KD* | 0.788 7 | 1.013 4 | 1.069 1 | 1.040 1 | 0.854 8 | |
| KB* | 0.784 0 | 0.853 3 | 0.791 3 | 0.650 5 | 0.300 9 | |
| G | 0.446 6 | 0.743 6 | 0.832 1 | 0.792 3 | 0.542 7 | |
| θB | θA | |||||
| - π/4 | - π/10 | 0 | π/10 | π/4 | ||
| - π/6 | K3* | 0.853 5 | 0.916 7 | 0.938 9 | 0.942 1 | 0.912 7 |
| KD* | 0.869 7 | 0.926 6 | 0.944 1 | 0.942 8 | 0.907 2 | |
| KB* | 1.463 7 | 1.285 7 | 1.132 7 | 0.967 3 | 0.710 1 | |
| G | 0.523 4 | 0.603 6 | 0.633 0 | 0.637 2 | 0.597 8 | |
| 0 | K3* | 0.973 0 | 1.045 7 | 1.073 6 | 1.082 0 | 1.058 9 |
| KD* | 0.984 6 | 1.050 5 | 1.073 6 | 1.077 3 | 1.047 9 | |
| KB* | 1.415 2 | 1.229 4 | 1.073 5 | 0.906 4 | 0.649 3 | |
| G | 0.679 9 | 0.785 1 | 0.827 4 | 0.840 2 | 0.804 5 | |
| π/6 | K3* | 0.868 3 | 0.946 6 | 0.978 7 | 0.991 6 | 0.975 3 |
| KD* | 0.874 5 | 0.946 0 | 0.973 4 | 0.981 7 | 0.959 3 | |
| KB* | 1.105 2 | 0.927 7 | 0.778 7 | 0.619 9 | 0.379 6 | |
| G | 0.541 4 | 0.643 2 | 0.687 5 | 0.705 5 | 0.682 3 | |
本文将辛离散有限元方法成功应用于电磁弹性复合材料在反平面荷载作用下的界面断裂分析中。该方法将传统有限元方法与哈密顿体系辛方法有机结合, 可以直接计算出高精度的应力、电场、磁场强度因子和能量释放率, 并同时获得裂纹尖端附近区域各物理场的显式表达式。相比其他数值方法, 该方法有三方面优势:①在裂纹尖端奇异区域内引入具有辛展开形式的解析解, 将该区域内传统有限元对应的大量节点未知量转化为少量辛本征解待定系数, 解决了传统有限元方法中断裂分析的网格敏感性问题, 并同时大幅提高了计算效率; ②引入的辛本征解函数能够直接表征裂纹尖端的奇异性, 避免了传统有限元方法中断裂参数计算的路径依赖性问题, 直接提高了应力强度因子计算精度; ③无需额外引进新的单元以及后处理程序, 可以直接获得裂纹尖端附近奇异物理场的显式表达式, 有利于该类结构的前期优化设计与后期安全评估。
附录A
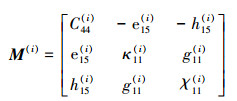
|
(A-1) |
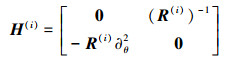
|
(A-2) |
式中
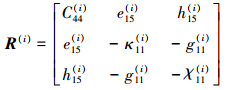
|
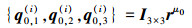
|
(A-3) |
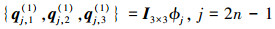
|
(A-4) |
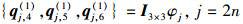
|
(A-5) |
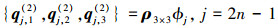
|
(A-6) |
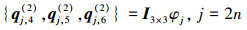
|
(A-7) |
式中,ϕj=rμjsin(μjθ), φj=rμjcos(μjθ); μj=j/2是辛本征值; ρ=(R(2))-1R(1), n=1, 2, 3, …。
| [1] | Nan C W, Bichurin M I, Dong S X, et al. Multiferroic Magnetoelectric Composites:Historical Perspective, Status, and Future Directions[J]. Journal of Applied Physics, 2008, 103(3): 031101-1-35. DOI:10.1063/1.2836410 |
| [2] |
裴永茂, 徐浩, 于泽军, 等. 磁电复合材料的力学实验与理论研究进展[J]. 固体力学学报, 2016, 37(3): 193-207.
Pei Yongmao, Xu Hao, Yu Zejun, et al. Research Progress in Mechanical Experiments and Theory of Magnetoelectric Composite Material[J]. Chinese Journal of Solid Mechanics, 2016, 37(3): 193-207. (in Chinese) |
| [3] |
胡克强, 李国强, 朱保兵. 压电-压磁板条中反平面裂纹的电-磁-弹性分析[J]. 工程力学, 2006, 23(5): 168-172.
Hu Keqiang, Li Guoqiang, Zhu Baobing. Electro-Magneto-Elastic Analysis of a Piezoelectromagnetic Strip with a Finite Crack under Longitudinal Shear[J]. Engineering Mechanics, 2006, 23(5): 168-172. (in Chinese) DOI:10.3969/j.issn.1000-4750.2006.05.029 |
| [4] |
郭怀民, 赵国忠. 有限高磁电弹性体中双半动态与静态裂纹分析[J]. 复合材料学报, 2015, 32(3): 888-895.
Guo Huaimin, Zhao Guozhong. Dynamic and Static Analysis for Two Semi-Infinite Cracks in Finite Magnetoelectroelastic Strip[J]. Acta Materiae Compositae Sinica, 2015, 32(3): 888-895. (in Chinese) |
| [5] | Li Y S, Feng W J, Xu Z H. Fracture Analysis of Cracked 2D Planar and Axisymmetric Problems of Magneto-Electro-Elastic Materials by the MLPG Coupled with FEM[J]. Computer Methods in Applied Mechanics and Engineering, 2009, 198(30): 2347-2359. |
| [6] | Rojas-Díaz R, Denda M, García-Sánchez F, et al. Dual BEM Analysis of Different Crack Face Boundary Conditions in 2D Magnetoelectroelastic Solids[J]. European Journal of Mechanics A-Solids, 2012, 31(1): 152-162. DOI:10.1016/j.euromechsol.2011.08.002 |
| [7] | Sladek J, Sladek V, Solek P, et al. Fracture Analysis of Cracks in Magneto-Electro-Elastic Solids by the MLPG,[J]. Computational Mechanics, 2008, 42: 697-714. DOI:10.1007/s00466-008-0269-z |
| [8] |
姚伟岸, 钟万勰. 辛弹性力学[M]. 北京: 高等教育出版社, 2002.
Yao Weian, Zhong Wanxie. Symplectic Elasticity[M]. Beijing: Higher Education Press, 2002. (in Chinese) |
| [9] | Xu C H, Zhou Z H, Leung A Y T, et al. The Finite Element Discretized Symplectic Method for Direct Computation of SIF of Piezoelectric Materials[J]. Engineering Fracture Mechanics, 2016, 162: 21-37. DOI:10.1016/j.engfracmech.2016.05.004 |
| [10] | Xu C H, Zhou Z H, Xu X S. Evaluation of Mode Ⅲ Interface Cracks in Magnetoelectroelastic Bimaterials by Symplectic Expansion[J]. Journal of Intelligent Material Systems and Structures, 2015, 26(11): 1417-1441. DOI:10.1177/1045389X14546659 |
| [11] | Wang B L, Mai Y W. Closed-Form Solution for an Antiplane Interface Crack between Two Dissimilar Magnetoelectroelastic Layers[J]. Journal of Applied Mechanics, 2006, 73(2): 281-290. DOI:10.1115/1.2083827 |
| [12] | Wang B L, Mai Y W. Exact and Fundamental Solution for an Anti-Plane Crack Vertical to the Boundaries of a Magnetoelectroelastic Strip[J]. International Journal of Damage Mechanics, 2007, 16(1): 77-94. DOI:10.1177/1056789507060781 |
| [13] | Wang B L, Han J C, Mai Y W. Mode Ⅲ Fracture of a Magnetoelectroelastic Layer:Exact Solution and Discussion of the Crack Face Electromagnetic Boundary Conditions[J]. International Journal of Fracture, 2006, 139(1): 27-38. DOI:10.1007/s10704-006-6632-1 |
2. School of Mechanics, Civil Engineering and Architecture, Northwestern Polytechnical University, Xi'an 710072, China


