加速寿命试验(accelrated life testing, ALT)通过增大试验件所受到的应力, 如温度、电压、压力等, 以便在更短的时间内获得相应的故障数据, 是获得高可靠性、长寿命产品失效数据的一种有效途径。茆诗松[1]与Voiculescu等[2]学者已经对加速寿命试验的数学模型进行了大量研究。在现有研究中, 通常仅考虑单一应力的影响, 但在工程实际中, 受试产品的寿命会受到多种环境应力综合效果影响。另外, 加速寿命试验要求产品的失效机理在试验过程中不发生改变[3], 当某一应力水平超过产品承受上限时, 产品失效机理就会发生变化, 所以单一应力水平不宜增加过高, 这样试验时间的缩短就会受到限制。因此, 为了增加试验效率, 提高试验结果的准确性, 有必要针对多应力加速寿命试验及其统计分析进行研究。张春华等[4-5]提出一种步降应力加速寿命试验方法, 该方法在损耗型长寿命产品试验中可显著提高试验效率。孙天宇等[6]在双应力交叉步加试验下研究了寿命服从威布尔分布部件可靠性指标的估计, 给出参数的Bayes估计。寇海霞等[7]提出一种双应力同步步降加速寿命试验方法来提高试验效率, 并针对威布尔分布产品进行仿真分析。Chen等[8]以气缸为对象开展双应力交叉步降加速寿命试验, 获得了气缸的可靠性指标并验证了加速模型的正确性。
以上研究均假设产品只有一种失效模式, 然而在工程实际中, 产品的失效往往是由多种失效模式导致, 因此有必要引入竞争失效模型, 在该模型中, 所观测到的失效数据由失效时间和失效机理标志两部分组成。竞争失效模型在医学、工程、计量经济学等很多领域得到了广泛应用, 目前, 国内外针对竞争失效模型在加速寿命试验中的应用已有很多研究。Han等[9]研究了指数分布下步进应力竞争失效模型, 给出参数的极大似然估计(maximum likelihood estimation, MLE)并构建了置信区间。张春芳等[10]研究了指数-威布尔分布的竞争失效模型, 分别应用极大似然估计方法和Bayes方法得到参数的点估计和区间估计。Alam等[11]在Ⅰ型和Ⅱ型截尾下讨论了Fréchet分布竞争失效部分加速寿命试验的统计分析问题。文献[12-14]分别分析了寿命服从威布尔分布、Lindley分布以及Kumaraswamy分布时的竞争失效模型。
在引入双应力竞争失效模型的同时, 为了进一步节省试验时间和成本, 还需要考虑截尾方案。最常用的截尾方案是Ⅰ型截尾(定时截尾)和Ⅱ型截尾(定数截尾), Epstein[15]首先提出综合Ⅰ型和Ⅱ型截尾的混合截尾方案。然而, 这几种截尾方案只在试验截止时移走未失效的试验件, 使得试验缺少灵活性。在之后被提出的逐步截尾方案中, 每次失效发生时, 均会随机移走一定数量的未失效试验件。Kundu等[16]结合逐步Ⅱ型截尾和混合截尾方案, 提出一种逐步Ⅱ型混合截尾方案, 避免了逐步截尾试验时间过长的问题。然而在这种方案中, 可能会出现失效样本数量过小的问题, 从而对数据的统计分析产生影响。于是, Ng等[17]提出了自适应Ⅱ型逐步截尾(adaptive type-Ⅱ progressive censoring, AT-Ⅱ PCS), 既能控制试验时间又能确保在试验中获得失效样本数量。近年来, AT-Ⅱ PCS的应用得到了广泛研究, 文献[18-20]分别讨论了广义Pareto分布、广义指数分布和Weibull分布的参数估计问题。Ren等[21]将AT-Ⅱ PCS和竞争失效模型相结合, 并通过数值模拟与试验数据验证了所提模型的正确性。
AT-Ⅱ PCS能够有效节省试验时间和成本, 但由于模型和计算的复杂性, 针对其在加速寿命试验中的应用研究仍然较少。因此, 本文在AT-Ⅱ PCS下考虑寿命服从Weibull分布的独立竞争失效产品, 建立起双应力恒加试验的统计分析方法。建立似然函数方程, 并采用Newton-Raphson迭代和渐进似然理论得到未知参数的MLE和渐进置信区间。采用Gibbs与M-H相结合的算法得到参数的Bayes估计, 并采用Monte Carlo(MC)方法构建参数的最大后验密度可信区间。最后, 通过数值模拟方法验证模型的正确性, 并比较在不同的试验方案下MLE与Bayes方法的参数估计效果。
1 模型描述 1.1 自适应Ⅱ逐步型截尾下双应力恒加试验假设有2组应力水平S1, S2满足
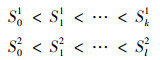
|
(1) |
式中: k和l分别表示2组加速应力的水平数; S01, S02分别为2组应力的正常应力水平。第一组应力中的第i个加速应力水平和第二组应力中的第j个加速应力水平的组合(S1i, S2j)称为水平组合, 简记为(i, j), i=1, 2, …, k, j=1, 2, …, l。水平组合共可以有kl个, 将n个参试样品分为kl组, 记每组样品数量为nij, 若只选择其中的部分水平组合进行恒加试验, 则样本量相应减少, 为了叙述方便, 假设有kl个水平组合。给定每组的预期失效数mij, 预期试验时间τij和逐步移走方案(Rij, 1, Rij, 2, …, Rij, mij)。试验过程中, 在第1个样品失效时刻tij, 1, 从剩余nij-1个未失效样品中随机移走Rij, 1个样品, 在第2个样品失效时刻tij, 2, 从剩余nij-Rij, 1-2个未失效样品中随机移走Rij, 2个样品, 以此类推, 直到第mij个失效时刻tij, mij, 移走剩下所有的未失效产品, 即Rij, mij=nij- 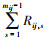
CaseⅠ 若tij, mij < τij, 试验结束, 移走方案不变, 这种情况等同于普通的逐步Ⅱ型截尾方案。
CaseⅡ 若tij, J < τij < tij, J+1, J=0, 1, 2, …, mij-1且tij, 0=0, 令RJ+1=RJ+2=…=Rmij-1=0, Rmij=nij-mij- 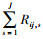
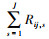
自适应Ⅱ型逐步截尾方案能保证每组最终的失效样本数为mij, 并且当试验时间超过τij后, 试验将尽可能快结束。
1.2 基本假设1) 共n个参试样品分为kl组, 在水平组合(i, j)下有nij个样品进行试验且 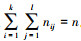
2) 每个样品的失效由m种独立失效机理的其中一种造成, 记水平组合(i, j)下m种失效机理的发生时间分别为Tij, 1, Tij, 2, …, Tij, m, 则样品的失效时间为min{Tij, 1, Tij, 2, …, Tij, m}。
3) 水平组合(i, j)下, Tij, 1, Tij, 2, …, Tij, m均服从两参数Weibull分布W(ηij, u, βu), 其中βu为形状参数, ηij, u为尺度参数, 分布函数(cumulative distribution function, CDF)和密度函数(probability density function, PDF)分别如(2)~(3)式所示。
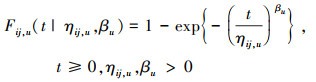
|
(2) |
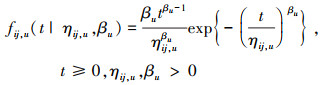
|
(3) |
4) 在各水平组合下产品失效机理一致, 即β11u=β12u=β21u=…=βu(u=1, 2, …, m)。
5) 第u个失效机理的加速模型为
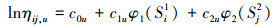
|
(4) |
式中: c0u, c1u, c2u, u=1, 2, …, m为待估参数; φ1, φ2为已知函数。
1.3 竞争失效模型基于1.2节中的假设, 在水平组合(i, j)下进行AT-Ⅱ PCS双应力恒加试验, 观测到的失效数据包含失效时间和失效机理标志, 即(tij, 1, αij, 1), (tij, 2, αij, 2), …, (tij, mij, αij, mij), 其中tij, 1, tij, 2, …, tij, mij为次序统计量, αij, s∈{1, 2, …, m}。令
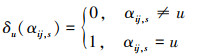
|
则水平组合(i, j)下由第u个失效机理造成的失效数为 
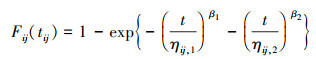
|
(5) |
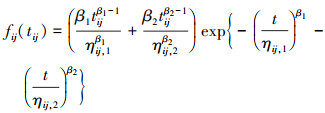
|
(6) |
产品的失效由失效模式1造成的概率为
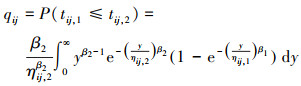
|
(7) |
由(7)式可得 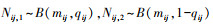
假设每个水平组合下至少有一个失效由第u个失效机理造成, 其似然函数为
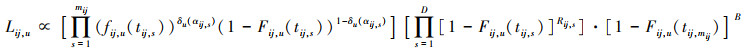
|
(8) |
式中
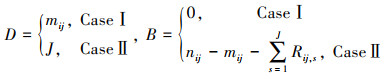
|
将(2)~(3)式代入(8)式得
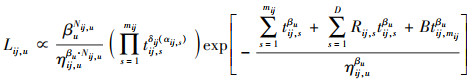
|
(9) |
第u个失效机理的完整似然函数和全部失效数据的完整似然函数分别为
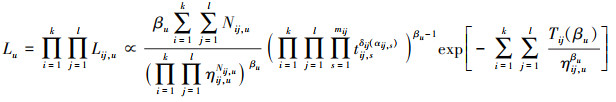
|
(10) |
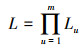
|
(11) |
式中
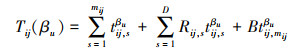
|
参数θ u=(βu, η11, u, η12, u, …, ηkl, u)的MLE记为 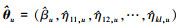
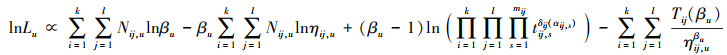
|
(12) |
(12) 式分别对参数βu, ηij, u求偏导并令偏导数为0, 可得以下方程组
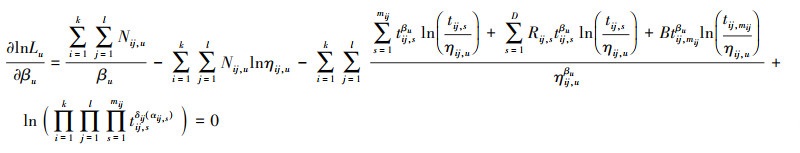
|
(13) |
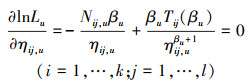
|
(14) |
采用Newton-Raphson迭代法求解(13)和(14)式即可得到参数的MLE。
定理1 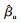
证明 由(13)式可得

|
对任意i, j, 均满足tij, mij≤ηij, u时
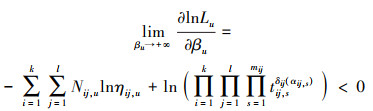
|
对任意i,j , 存在tij, mij>ηij, u时
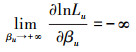
|
故 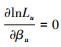
(12) 式对βu求二阶导得
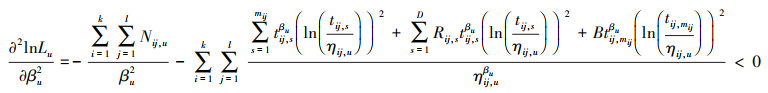
|
故 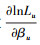
由(14)式得ηij, u的极大似然估计 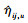
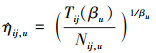
|
(15) |
ηij, u, βu>0, 因此对于确定的βu, 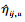
由于参数极大似然估计的精确分布推导复杂, 计算困难, 难以获得参数的精确区间估计, 本节采用渐进似然理论构建参数的渐进置信区间。通过对参数的观测Fisher信息矩阵求逆获得参数的渐进方差-协方差矩阵。
参数 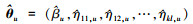
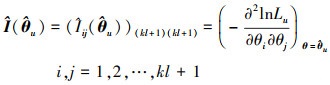
|
(16) |
参数MLE的方差-协方差矩阵为
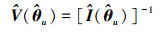
|
矩阵 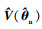
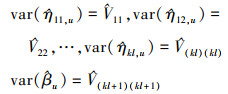
|
对给定的置信水平100(1-γ)%, 参数 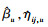
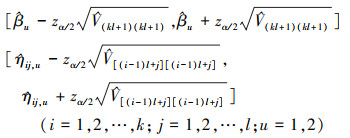
|
zα/2是标准正态分布的α/2分位数。
3 Bayes估计 3.1 后验分布Bayes方法能结合先验信息与样本信息对未知参数进行估计, 是传统估计方法的一种有效替代方法。本节采用Bayes方法, 在平方损失函数下获取参数 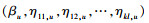
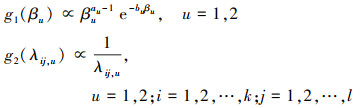
|
其中, 超参数au, bu均为非负常数。于是参数 ωu=(βu, λ11, u, λ12, u, …, λkl, u)联合先验分布表示为
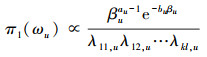
|
(17) |
根据(10)和(17)式得到参数联合后验密度函数
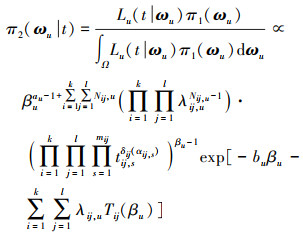
|
(18) |
式中
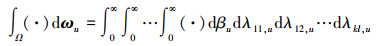
|
由于后验分布的形式十分复杂, 难以求得Bayes估计的显式表达式, 故而采用Gibbs抽样算法来解决这一问题。
3.2 Gibbs抽样算法由(18)式可以得到(βu, λ11, u, λ12, u, …, λkl, u)等参数的全条件密度
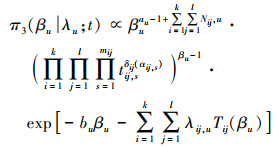
|
(19) |
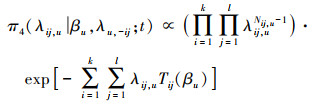
|
(20) |
式中
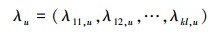
|
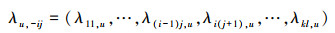
|
βu的全条件密度是对数凹函数, 证明详见文献[22], 并且由(20)式可知λij, u的全条件密度服从参数为Nij, u和Tij(βu)的Gamma分布。通过Gibbs抽样得到后验分布随机样本的流程如下
Step1 给定参数的初值(β(0)u, λ11, u(0), …, λkl, u(0)), 可以选择MLE的结果作为初值;
Step2 设置迭代步数q=0;
Step3 采用Metropolis-Hasting(M-H)算法(或自适应拒绝抽样)从 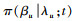
Step4 从 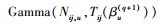
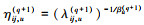
Step5 重复Step3~4 Ng次, 并且给定预烧期A(burnin period), 最终得到平方损失下参数的Bayes估计
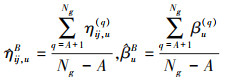
|
(21) |
根据文献[23]提出的MC方法, HPD可信区间构建方法如下:
1) 将Gibbs抽样中得到的 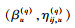
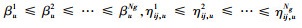
2) 计算100(1-α)%的可信区间[βuq, βuq+(1-α)·Ng], 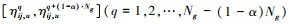
3) 从 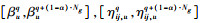
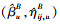
正常应力下参数η00, u的估计值由(22)式计算得到
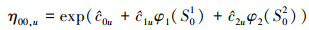
|
(22) |
再利用最小二乘法获得参数 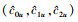
令 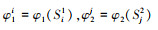

|
(23) |
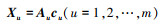
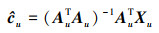
|
(24) |
本节采用数值模拟评估所提的MLE与Bayes估计方法的表现。考虑以温度和电压作为加速应力, 每组应力有4个加速应力水平, 分别为
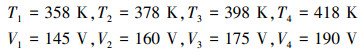
|
正常应力水平为T0=338 K, V0=125 V。应力水平组合为{(1, 2), (3, 1), (2, 4), (4, 3)}, 每个水平组合下投入的样本量nij, 预定失效数mij, 移走方案Rij和预期时间τij见表 1, 每组方案分别在预期时间为τ1, τ2时进行AT-Ⅱ PCS恒加试验。
| 方案1 | 方案2 | 方案3 |
| n12=n31=n24=n43=30 | n12=n31=n24=n43=30 | n12=n31=n24=n43=40 |
| m12=m31=m24=m43=15 | m12=m31=m24=m43=25 | m12=m31=m24=m43=20 |
| R12=R31=R24=R43=(1×15) | R12=R31=R24=R43=(1×2, 0×20, 1×3) | R12=R31=R24=R43=(1×20) |
| τ1=(τ12=200, τ31=25, τ24=25, τ43=4) | ||
| τ2=(τ12=450, τ31=60, τ24=60, τ43=9) |
假定产品有2种失效模式, 加速方程为
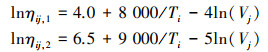
|
由加速方程得尺度参数分别为
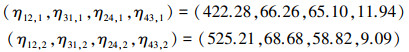
|
形状参数的值取为β1=1.5, β2=1.6。在应力水平组合(i, j)下, 产品的失效数据由以下步骤获得:
1) 根据方案给定的样本量nij, 预定失效数mij, 移走方案Rij, 从PDF为(6)式的竞争失效Weibull分布中抽取Ⅱ型逐步截尾样本tij, 1, tij, 2, …, tij, mij, 详细过程见文献[24];
2) 根据预期时间τ, 找出满足tij, J < τij < tij, J+1的J, 舍弃tij, J+2, tij, J+3, …, tij, mij;
3) 从截断分布fij(tij)/[1-Fij(tij, J+1)]中抽取样本量为 
4) 根据(7)式得Nij, 1~B(mij, qij), 由此抽取一组失效机理标志(αij, 1, αij, 2, …, αij, mij)。
为了克服随机性, 整个模拟过程重复1 000次。计算Bayes估计时, 形状参数βu的先验取Gamma分布, 尺度参数ηij取无信息先验, Gibbs算法中迭代次数Ng=2 000预烧期A=200, 提议分布为正态分布。计算得到的点估计平均值, 估计的均方根误差(root mean squared error, RMSE)和显著性水平α=0.05时的平均置信区间长度(mean interval length, MIL)如表 2所示。RMSE按(25)式计算
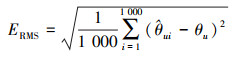
|
(25) |
| 方案 | 参数 | τ1=(200, 25, 25, 4) | τ2=(450, 60, 60, 9) | |||
| MLE(RMSE)MIL | Bayes(RMSE)MIL | MLE(RMSE)MIL | Bayes(RMSE)MIL | |||
| (30, 15) | β1 | 1.502 4(0.288 3) 0.904 9 |
1.547 6(0.217 6) 0.732 1 |
1.604 8(0.263 6) 0.917 9 |
1.595 2(0.204 0) 0.733 5 |
|
| η12, 1 | 552.013 0(1 072.7) 684.114 4 |
539.768 1(208.021 4) 545.535 9 |
450.110 6(93.702 8) 414.792 7 |
487.782 6(122.479 5) 457.916 7 |
||
| η31, 1 | 132.748 1(1 383.9) 100.459 6 |
94.026 2(47.499 0) 102.687 7 |
70.508 0(15.307 6) 70.664 4 |
77.691 8(20.971 9) 79.229 0 |
||
| η24, 1 | 93.109 3(273.606 1) 153.675 4 |
91.601 9(45.242 0) 108.300 6 |
70.456 5(17.700 2) 76.383 6 |
78.631 0(24.795 7) 87.060 4 |
||
| η43, 1 | 14.022 1(34.578 9) 24.587 7 |
14.240 3(4.270 3) 17.682 6 |
12.474 7(2.736 1) 14.378 7 |
14.007 1(3.727 5) 16.356 6 |
||
| β2 | 1.535 2(0.273 4) 0.897 8 |
1.585 5(0.189 6) 1.109 5 |
1.618 3(0.316 4) 0.902 9 |
1.645 3(0.187 5) 0.739 4 |
||
| η12, 2 | 740.289 3(2 246.5) 787.253 0 |
675.882 0(262.539 8) 787.211 7 |
573.234 9(136.889 6) 655.199 1 |
629.450 6(181.604 9) 711.014 0 |
||
| η31, 2 | 90.814 0(42.571 9) 104.040 5 |
97.106 1(48.007 0) 106.735 7 |
74.574 6(17.842 0) 78.393 5 |
80.798 8(22.686 3) 83.941 7 |
||
| η24, 2 | 73.224 1(30.203 8) 78.707 2 |
77.997 6(34.558 2) 79.758 9 |
63.219 6(14.520 8) 61.571 5 |
67.782 8(17.925 7) 65.303 1 |
||
| η43, 2 | 9.608 3(1.956 0) 9.372 5 |
10.104 7(2.165 8) 9.431 3 |
9.712 5(2.060 6) 8.921 6 |
10.323 4(2.487 8) 9.328 5 |
||
| (30, 25) | β1 | 1.561 3(0.214 6) 0.722 8 |
1.578 9(0.190 6) 0.600 3 |
1.603 2(0.230 7) 0.742 3 |
1.596 1(0.197 4) 0.603 4 |
|
| η12, 1 | 449.643 3(96.033 9) 326.008 8 |
468.296 2(108.560 3) 326.761 4 |
435.897 5(74.381 3) 294.248 9 |
455.632 5(85.785 3) 313.009 8 |
||
| η31, 1 | 73.813 4(18.203 1) 56.509 6 |
77.400 3(21.080 9) 58.245 2 |
69.219 3(14.362 3) 50.361 8 |
72.887 1(16.701 4) 54.263 9 |
||
| η24, 1 | 71.018 0(16.912 9) 60.941 7 |
74.881 9(19.853 3) 60.113 1 |
66.879 5(11.926 5) 51.044 7 |
70.795 3(14.251 0) 55.707 9 |
||
| η43, 1 | 12.049 9(1.955 3) 10.505 4 |
12.806 6(2.325 4) 11.041 5 |
11.999 2(2.068 1) 10.004 5 |
12.828 9(2.476 0) 11.008 2 |
||
| β2 | 1.578 4(0.214 0) 0.708 6 |
1.609 5(0.182 6) 0.601 3 |
1.617 7(0.200 3) 0.737 1 |
1.623 4(0.166 4) 0.607 8 |
||
| η12, 2 | 557.685 8(125.159 0) 474.039 1 |
587.400 5(144.606 2) 486.271 9 |
539.178 2(98.574 9) 426.385 0 |
572.499 4(118.745 4) 469.471 5 |
||
| η31, 2 | 76.369 6(18.122 4) 59.242 6 |
79.954 7(20.903 0) 60.816 1 |
71.824 2(13.984 2) 52.373 9 |
75.603 8(16.393 8) 57.109 1 |
||
| η24, 2 | 63.716 8(14.805 9) 45.785 2 |
66.414 7(16.583 7) 47.614 8 |
60.967 1(10.605 8) 42.529 7 |
63.879 3(12.139 5) 45.417 7 |
||
| η43, 2 | 9.200 4(1.392 8) 6.194 4 |
9.539 9(1.530 8) 63.508 |
9.184 3(1.399 7) 5.963 8 |
9.551 0(1.548 4) 6.298 8 |
||
| (40, 20) | β1 | 1.527 7(0.403 1) 0.775 7 |
1.524 0(0.257 3) 0.652 9 |
1.590 5(0.226 6) 0.784 6 |
1.606 0(0.202 8) 0.648 6 |
|
| η12, 1 | 511.787 8(308.813 5) 458.716 7 |
511.679 8(194.976 9) 444.605 7 |
440.731 8(85.731 6) 352.423 4 |
463.863 6(98.095 8) 368.657 6 |
||
| η31, 1 | 87.987 4(75.294 2) 83.705 5 |
87.292 4(38.388 1) 82.021 7 |
69.136 7(13.806 5) 60.211 2 |
73.465 1(16.617 9) 63.292 8 |
||
| η24, 1 | 83.114 7(76.906 0) 84.858 9 |
83.546 7(36.592 3) 83.564 9 |
68.846 0(15.270 1) 64.808 0 |
73.773 5(18.888 7) 68.409 5 |
||
| η43, 1 | 12.801 4(6.977 0) 14.081 1 |
13.377 7(3.598 8) 14.343 9 |
12.503 2(2.793 0) 12.864 0 |
13.585 5(3.588 2) 13.826 0 |
||
| β2 | 1.555 6(0.236 2) 0.774 6 |
1.549 0(0.255 5) 0.653 9 |
1.592 2(0.200 3) 0.773 6 |
1.624 9(0.168 2) 0.653 5 |
||
| η12, 2 | 618.147 4(216.924 4) 650.643 6 |
642.510 8(235.304 4) 663.243 1 |
557.479 2(117.609 2) 552.530 6 |
593.941 6(138.070 4) 575.832 2 |
||
| η31, 2 | 86.958 4(32.966 9) 84.558 5 |
90.352 7(37.444 8) 85.740 0 |
72.655 4(15.926 4) 65.955 8 |
77.066 2(18.973 6) 68.797 8 |
||
| η24, 2 | 71.578 9(27.379 6) 65.013 2 |
73.877 9(30.454 7) 66.349 7 |
62.210 3(12.568 1) 52.736 2 |
65.330 5(14.486 9) 54.370 5 |
||
| η43, 2 | 9.444 3(1.649 5) 7.764 9 |
9.697 5(2.083 7) 7.960 0 |
9.400 4(1.615 4) 7.353 9 |
9.808 6(1.816 3) 7.542 2 |
||
式中: 
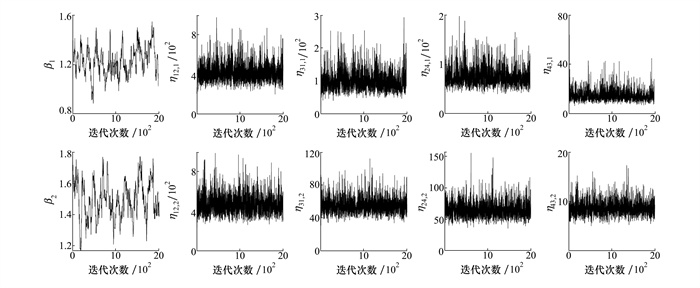
图 1给出了方案3中当τ=τ2时Gibbs采样算法中的迭代路径图, 各参数的值在均值附近上下波动, 表明算法中的马尔科夫链已经充分混合, 并收敛到平稳分布。
|
| 图 1 参数的迭代路径图 |
从表 2中可以得到以下几点结论:
1) 随着样本数量增大, 或者mij/nij值增大时, 2种估计方法对尺度参数ηij的点估计均值更加接近真值, 同时RMSE和平均置信区间长度减小, 说明失效样本数量的增加能够提高估计的准确性。
2) 在同样的(nij, mij)下, 当预期时间从τ1增加到τ2时, 2种方法对于尺度参数ηij, 1, ηij, 2的点估计均值更接近真值, 同时RMSE与平均置信区间长度减小。这是由于τ=τ1时试验结束得快, 使得观测到的失效数据较τ=τ2时更小, 因此估计误差也相对较大。
3) 2种估计方法对形状参数β1, β2的估计效果在各种方案下没有显著差异, 即失效样本的增加不会使形状参数的估计更准确, 在实际应用中应利用设计经验或是先验信息对形状参数的估计做出更多改进与修正。
4) 当mij/nij较小(如方案1和方案3)且试验预期时间τ较小时, MLE得到的结果波动较大, 特别是试验得到一些极端数据时(例如最后一个失效样本的失效时间很小), 在采用Newton-Raphson迭代求解MLE时会得到异常值甚至出现迭代不收敛的情况, 此时Bayes估计的效果优于MLE。而当试验预期时间τ较大或mij/nij较大时, 2种估计方法的效果均能够接受, 但整体上MLE对于尺度参数的估计值较Bayes估计更接近真值, MSE和MIL也较小, 此类情况下MLE优于本文所给先验组合下的Bayes估计。
表 3给出了基于上述模拟结果进行拟合得到的加速方程中未知系数的估计值, 根据加速方程外推得到常应力下的特征寿命估计值以及使用时长分别为500, 1 500和3 000 h时产品的可靠度估计值。方案1中τ=τ1时MLE的估计结果误差较大, 故省略该情形下的估计值。从表 3可以发现各水平组合(i, j)下失效样本数量以及试验预期时间τ对于估计准确性有显著影响。在各方案下MLE与Bayes估计对可靠度的估计值均呈现略微偏大的趋势, 随着mij/nij和τ的增加, 估计的结果逐渐接近于真值。
| 方案 | c01 | c11 | c21 | c02 | c12 | c22 | R(500) | R(1 500) | R(3 000) | ||
| (30, 15) | τ1=(200, 25, 25, 4) | MLE | 11.17 | 7 942.62 | -5.30 | 7.90 | 9 593.44 | -5.52 | |||
| Bayes | 3.71 | 7 936.16 | -3.89 | 6.81 | 9 085.03 | -5.09 | 0.958 1 | 0.789 2 | 0.498 5 | ||
| τ2=(450, 60, 60, 9) | MLE | 3.76 | 8 054.20 | -3.97 | 6.77 | 9 038.74 | -5.06 | 0.962 6 | 0.800 2 | 0.506 9 | |
| Bayes | 3.63 | 7 983.20 | -3.89 | 7.03 | 9 105.75 | -5.13 | 0.966 4 | 0.819 4 | 0.545 2 | ||
| (30, 25) | τ1=(200, 25, 25, 4) | MLE | 4.54 | 8 094.72 | -4.14 | 7.13 | 9 079.41 | -5.15 | 0.962 3 | 0.806 8 | 0.529 6 |
| Bayes | 4.49 | 8 053.44 | -4.10 | 7.26 | 9 111.39 | -5.18 | 0.966 1 | 0.820 9 | 0.552 6 | ||
| τ2=(450, 60, 60, 9) | MLE | 4.36 | 8 044.49 | -4.09 | 6.73 | 9 025.76 | -5.05 | 0.961 5 | 0.794 8 | 0.497 6 | |
| Bayes | 4.32 | 7 997.93 | -4.05 | 6.86 | 9 069.13 | -5.09 | 0.963 4 | 0.805 2 | 0.517 9 | ||
| (40, 20) | τ1=(200, 25, 25, 4) | MLE | 5.11 | 8 224.85 | -4.29 | 7.56 | 9 232.66 | -5.29 | 0.970 7 | 0.851 4 | 0.627 4 |
| Bayes | 4.84 | 8 138.86 | -4.20 | 7.72 | 9 254.73 | -5.33 | 0.969 3 | 0.845 6 | 0.616 0 | ||
| τ2=(450, 60, 60, 9) | MLE | 3.80 | 8 001.11 | -3.95 | 6.57 | 9 056.80 | -5.03 | 0.958 7 | 0.785 1 | 0.482 5 | |
| Bayes | 3.71 | 7 936.16 | -3.89 | 6.81 | 9 096.03 | -5.09 | 0.962 9 | 0.801 3 | 0.508 4 | ||
| 真值 | 4 | 8 000 | -4 | 6.5 | 9 000 | -5 | 0.949 2 | 0.757 1 | 0.448 8 |
本文提出了寿命服从Weibull分布的竞争失效产品在自适应Ⅱ型逐步截尾下双应力恒加试验的统计分析方法。首先建立似然函数方程, 通过Newton-Raphson迭代得到Weibull分布中未知参数的MLE, 基于渐进似然理论构建参数的渐进置信区间。其次, 在形状参数的先验分布为Gamma分布, 尺度参数取无信息先验的条件下获得参数的后验密度函数, 采用Gibbs采样与M-H抽样结合的算法在平方损失下计算参数的Bayes估计, 并基于MC方法建立参数的HPD可信区间。最后通过数值模拟验证了所提方法的可行性, 结果表明: ①预期试验时间τ对于参数估计效果有显著影响, 特别是当失效样本数mij占投入样本数量nij的比例较小时, 过小的τ会使MLE产生较大波动, 此时建议优先考虑使用Bayes估计。②当失效样本数量较大时, 2种估计均有良好的表现且MLE的估计效果略优于本文所给先验组合下的Bayes估计。
| [1] | MAO Shisong. Analysis of constant stress AFT for Weibull distribution[J]. Chinese Journal of Qualty and Reliabicity, 2003, 6: 16-23. |
| [2] | VOICULESCU S, GUERIN F, BARREAU M, et al. Bayesian estimation in accelerated life testing application on exponential-arrhenius model[J]. International Journal of Product Development, 2009, 7(3/4): 246-260. DOI:10.1504/IJPD.2009.023321 |
| [3] |
马纪明, 阮凌燕, 付永领, 等. 航空液压泵加速寿命试验现状[J]. 液压与气动, 2015(6): 6-12.
MA Jiming, RUAN Lingyan, FU Yongling, et al. Current status of accelerated life testing for aviation hydraulic pumps[J]. Chinese Hydraulics & Pneumatics, 2015(6): 6-12. (in Chinese) DOI:10.11832/j.issn.1000-4858.2015.06.002 |
| [4] |
张春华, 陈循, 温熙森. 步降应力加速寿命试验(上篇)——方法篇[J]. 兵工学报, 2005(5): 661-665.
ZHANG Chunhua, CHEN Xun, WEN Xisen. Step-down-stress accelerated life testing——methodology[J]. Acta Armamentarii, 2005(5): 661-665. (in Chinese) DOI:10.3321/j.issn:1000-1093.2005.05.019 |
| [5] |
张春华, 陈循, 温熙森. 步降应力加速寿命试验(下篇)——统计分析篇[J]. 兵工学报, 2005(5): 666-669.
ZHANG Chunhua, CHEN Xun, WEN Xisen. Step-down-stress accelerated life testing——statistical analysis[J]. Acta Armamentarii, 2005(5): 666-669. (in Chinese) DOI:10.3321/j.issn:1000-1093.2005.05.020 |
| [6] |
孙天宇, 师义民, 谢奇. Weibull分布下双应力交叉步加试验的可靠性分析[J]. 机械强度, 2013, 35(3): 253-257.
SUN Tianyu, SHI Yimin, XIE Qi. Analysis of reliability performances on two alternative step-stress accelerated life test for Weibull distribution[J]. Journal of Mechanical Strength, 2013, 35(3): 253-257. (in Chinese) |
| [7] |
寇海霞, 安宗文, 刘波. 双应力同步步降加速寿命试验方法[J]. 电子科技大学学报, 2016, 45(2): 316-320.
KOU Haixia, AN Zongwen, LIU Bo. Double synchronous-step-down-stress accelerated life testing method[J]. Journal of University of Electronic Science and Technology of China, 2016, 45(2): 316-320. (in Chinese) DOI:10.3969/j.issn.1001-0548.2016.03.027 |
| [8] | CHEN Juan, LI Jia, Wang Deyi, et al. Double crossed step-down-stress accelerated life testing for pneumatic cylinder based on cumulative damage model[J]. Advanced Materials Research, 2014, 871: 56-63. |
| [9] | HAN D, BALAKRISHNAN N. Inference for a simple step-stress model with competing risks for failure from the exponential distribution under time constraint[J]. Computational Statistics & Data Analysis, 2010, 54(9): 2066-2081. |
| [10] |
张春芳, 师义民, 吴敏. 逐步Ⅰ型混合截尾下指数-威布尔分布竞争失效模型的统计分析[J]. 应用概率统计, 2018, 34(4): 331-344.
ZHANG Chunfang, SHI Yimin, WU Min. Statistical inference on competing risks model from exponentiated Weibull distribution under type-Ⅰ progressive hybrid censoring data[J]. Chinese Journal of Applied Probability and Statistics, 2018, 34(4): 331-344. (in Chinese) DOI:10.3969/j.issn.1001-4268.2018.04.001 |
| [11] | ALAM I, ANWAR S, SHARMA L K, et al. Competing risk analysis in constant stress partially accelerated life tests under censored information[J]. Annals of Data Science, 2023, 10(5): 1379-1403. DOI:10.1007/s40745-022-00401-z |
| [12] | PAREEK B, KUNDU D, KUMAR S. On progressively censored competing risks data for Weibull distributions[J]. Computational Statistics & Data Analysis, 2009, 53(12): 4083-4094. |
| [13] |
黄文平, 周经伦, 宁菊红, 等. 基于竞争失效数据的Lindley分布参数估计[J]. 系统工程与电子技术, 2016, 38(2): 464-469.
HUANG Wenping, ZHOU Jinglun, NING Juhong, et al. Parameter estimation of Lindley distribution with competing risk data[J]. Systems Engineering and Electronics, 2016, 38(2): 464-469. (in Chinese) |
| [14] | WANG Liang. Inference of progressively censored competing risks data from Kumaraswamy distributions[J]. Journal of Computational And Applied Mathematics, 2018, 343: 719-736. DOI:10.1016/j.cam.2018.05.013 |
| [15] | EPSTEIN B. Truncated life tests in the exponential case[J]. The Annals of Mathematical Statistics, 1954, 25: 555-564. DOI:10.1214/aoms/1177728723 |
| [16] | KUNDU D, JOARDER A. Analysis of type-Ⅱ progressively hybrid censored data[J]. Computational Statistics & Data Analysis, 2006, 50. |
| [17] | NG H, KUNDU D, PING S C. Statistical analysis of exponential lifetimes under an adaptive type-Ⅱ progressive censoring scheme[J]. Naval Research Logistics, 2010, 56(8): 687-698. |
| [18] | MAHMOUD A W M, SOLIMAN A A, ABD ELLAH A, et al. Estimation of generalized pareto under an adaptive type-Ⅱ progressive censoring[J]. Intelligent Information Management, 2013, 5: 73-83. DOI:10.4236/iim.2013.53008 |
| [19] | MOHIEELDIN M M M, AMEIN M, SHAFAY A R, et al. Estimation of generalized exponential distribution based on anadaptive progressively type-Ⅱ censored sample[J]. Journal of Statistical Computatian and Simulation, 2017, 87: 1292-1304. DOI:10.1080/00949655.2016.1261863 |
| [20] | NASSAR M, ABO-KASEM O E, ZHANG C, et al. Analysis of weibull distribution under adaptive type-Ⅱ progressive hybrid censoring scheme[J]. Journal of the Indian Society for Probability and Statistics, 2018(2): 1-41. |
| [21] | REN Junru, GUI Wenhao. Statistical analysis of adaptive type-Ⅱ progressively censored competing risks for weibull models[J]. Applied Mathematical Modelling, 2021, 98: 323-342. DOI:10.1016/j.apm.2021.05.008 |
| [22] | WU Min, SHI Yiming, SUN Yudong. Inference for accelerated competing failure models from Weibull distribution under type-Ⅰ progressive hybrid censoring[J]. Journal of Computational & Applied Mathematics, 2014, 263: 423-431. |
| [23] | CHEN Minghui, SHAO Qiman. Monte Carlo estimation of Bayesian credible and HPD intervals[J]. Journal of Computational & Graphical Statistics, 1999, 8(1): 69-92. |
| [24] | BALAKRISHNAN N, SANDU R A. A simple simulation algorithm for generating progressive type-Ⅱ censored samples[J]. The American Stueistician, 1995, 49: 229-230. DOI:10.1080/00031305.1995.10476150 |




