2. 上海宇航系统工程研究所, 上海 201108
发展可重复使用的运载器能够大大降低发射成本及发射周期, 是实现低成本进入太空的重要途径之一。使用火箭发动机作为动力的部分可重复使用运载器是一个主要发展方向, 尤其是火箭动力的两级入轨可重复使用运载器[1]。火箭的一子级垂直着陆任务, 一方面需要在推力受限的情况下实现减速和调节, 另一方面需要满足终端垂直定点着陆的状态约束(位置、速度、姿态)。对于这种复杂约束下的控制问题, 需要采用自主性更好、适应能力更强的制导方法。随着“计算制导与控制”[2]概念的发展, 以在线实时轨迹规划为基础的闭环制导成为一种新的可行途径。
轨迹规划方法一般可以分为间接法和直接法。间接法通常基于庞特里亚金极大值定理将最优控制问题转化为两点边值问题进行求解。间接法在计算精度及计算时间上具有一定的优势, 但对初始猜测极为敏感, 并且较难处理复杂的模型与约束。直接法通过离散控制量和状态量, 将最优控制问题转化为一般的非线性规划问题进行求解。直接法中的伪谱方法以全局插值多项式为基函数, 在选定的正交配点上近似状态量和控制量, 实现问题的转化。伪谱方法可以避免龙格现象且离散精度更高, 所以多种伪谱方法被应用在月球及火星的着陆问题中[3-4]。然而, 伪谱方法只是一种离散方法, 大规模非线性规划问题的求解并不依赖于此过程。
对于具有凸结构的一类问题, 尤其是二阶锥规划问题, 直接法中的凸优化算法可以高效可靠求解。在关于着陆问题的研究中, Acikmese等[5]将凸优化算法应用在火星有动力着陆的轨迹优化问题中, 对非凸的推力上下限约束实现了“无损凸化”。对于火箭一子级着陆这样的非线性动力学系统, Liu[6]对动力学方程进行逐次线性化和逐次近似, 将非凸问题转化为一系列凸子问题进行求解, 这种方法也被称为序列凸优化算法(sequential convex programming, SCP)。在此基础上, 伪谱离散[7-8]、虚拟控制[9]、信赖域更新[10]等技巧被引入序列凸优化算法以改善精度与收敛性。针对火箭垂直着陆的问题, 以上述序列凸优化算法为基础设计了多种闭环制导方法[11-13], 这些方法存在只考虑纵向平面动力学模型, 或需要较强凸化经验等不足。同时, 快速性始终是轨迹优化算法能否在线应用的重要考量因素, 而目前的数值仿真计算平台与实际箭载平台计算能力具有一定差距。因此, 轨迹优化算法的计算效率仍需进一步提高。
近年来, Ma等[14-15]将改进切比雪夫-皮卡迭代法(modified Chebyshev-Picard iteration, MCPI)与高斯-牛顿法结合, 提出一种改进的并行结构牛顿类算法。这种算法可以快速求解问题得到可行解, 相对于凸优化算法具有更高的计算效率。该算法应用在导弹末制导、运载火箭上升段场景时, 表现出较好的计算效率、计算精度及鲁棒性。
因此, 针对存在推力约束和终端约束的火箭子级垂直着陆问题, 本文结合具有并行结构的牛顿类算法的思路, 提出一种改进的基于二阶皮卡-切比雪夫-牛顿类算法的制导方法。微分动力学方程的二阶皮卡迭代格式不仅可以使得不同时刻的状态量彼此独立, 而且可以使得状态量表达式显式包含控制量。同时, 以切比雪夫多项式作为基函数, 对二阶皮卡迭代格式的动力学方程进行离散, 以此来提高算法的离散精度。经过上述的步骤, 将问题构建为非线性最小二乘问题, 采用高斯-牛顿法求解, 引入投影方法实现推力限幅, 得到待求解变量的显式表达式来迭代求解。最后, 以上述算法为基础, 结合制导策略实现火箭垂直着陆的闭环制导。采用提出方法和序列凸优化算法进行了优化对比分析, 验证了提出方法的性能; 并对本文制导方法进行了闭环制导仿真, 验证闭环制导方法的有效性。
1 火箭一子级垂直着陆动力学模型本文研究火箭一子级垂直定点着陆问题, 首先建立着陆固联坐标系和三自由度动力学方程。因为垂直着陆段初始位置和速度相对均较小, 所以忽略过程中的热流约束和动压约束。同时, 着陆阶段的飞行距离和时间范围较小, 因此忽略地球自转产生的牵连加速度和科氏加速度。
着陆固联坐标系原点与着陆点O固联, Ox轴在预先设定的着陆点水平面内, Oy轴垂直于着陆点水平面指向正上方, Oz轴与xOy面垂直并构成右手坐标系。着陆固联坐标系的动力学方程(1)式所示
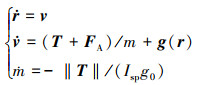
|
(1) |
式中: r为位置矢量;v为速度矢量;m为质量; Isp为比冲;g0为海平面引力加速度。推力矢量T与火箭纵轴方向一致。火箭飞行过程中受到的气动力在箭体坐标系表示, 箭体坐标系以火箭质心为原点O1, O1x1轴沿体轴指向箭体头部, O1y1轴在火箭主对称平面内垂直于O1x1轴, O1z1轴与x1O1y1面垂直并构成右手坐标系。因为着陆过程中箭体处于小攻角状态, 所以只考虑轴向气动力FA, 其数值表达式为
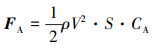
|
(2) |
式中: ρ为大气密度(标准大气模型);V为速度大小;S为参考面积;CA为轴向气动力系数。引力加速度表示为

|
(3) |
R为当前点地心矢径在着陆坐标系的矢量形式,R为地心距,μ为地球引力常数。在着陆过程中, 火箭的推力T存在幅值约束

|
(4) |
同时, 为了满足精确着陆的要求, 火箭的终端状态约束如(5)式所示

|
(5) |
式中: rf*, vf*分别为期望终端位置、速度;mdry为火箭的干质量。
因此, 基于动力学方程(1)式, 考虑终端误差最小, 火箭一子级垂直定点着陆的轨迹优化问题可以概括描述为

|
(6) |
式中: 状态变量定义为x=[rT, vT, m], 控制变量定义为u=[ϕ, ψ, η], 其中俯仰角ϕ、偏航角ψ用来调节推力方向, 节流比η用来调节推力大小。终端的状态误差(包括位置、速度)用ψ(x(tf))表示。
2 火箭垂直着陆制导方法本节提出以二阶皮卡-切比雪夫-牛顿类算法为基础的闭环制导方法。将着陆过程的动力学方程采用二阶皮卡迭代格式表示, 使得各状态量显式包含控制量, 且不同时刻的状态量之间彼此独立。然后将动力学方程基于切比雪夫多项式离散化, 并将离散问题转化为非线性最小二乘问题, 引入投影方法处理推力约束并采用牛顿类算法迭代求解。最终, 以上述算法过程为基础, 结合制导策略, 提出火箭垂直着陆的闭环制导方法。
2.1 基于二阶皮卡迭代的微分方程求解皮卡迭代是一种求解常微分方程的方法。与欧拉法、龙格库塔方法不同, 皮卡迭代的迭代格式可以使得不同时间的状态量彼此独立。具体地说, 在第k次迭代中, 当前时刻的状态量并不依赖于上一时刻的状态量, 均与已知的参考状态序列(即上一次迭代的状态序列)有关。
将(1)式的动力学方程简写为如下形式
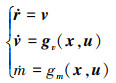
|
(7) |
式中: gv(x, u)表示速度微分方程; gm(x, u)表示质量微分方程。(7)式的等价积分形式为

|
(8) |
采用自然一阶系统的皮卡迭代, (8)式的迭代格式为[16-17]
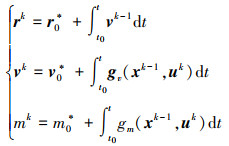
|
(9) |
可以看出, 参考(9)式的迭代格式, 基于参考状态序列xk-1和控制序列uk, 可以更新得到新的状态序列xk。
高斯-牛顿法的求解过程中, 需要得到雅可比矩阵, 即终端约束方程关于待求解变量的一阶导数信息。但由(9)式的一阶皮卡迭代格式可以看出, 控制量并未显式表示在位置量中, 这会使得后续雅可比矩阵发生奇异且问题不可解。与文献[14-15]不同的是, 本文提出的算法采用自然二阶系统的皮卡迭代格式来处理这一问题, 其具体公式为
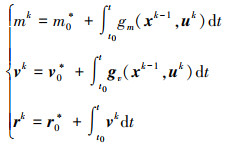
|
(10) |
将(10)式中vk的表达式代入rk得

|
(11) |
(11) 式即为完整的二阶皮卡迭代格式的动力学方程, 也是控制序列更新后计算状态序列的方法。因此, 着陆过程位置、速度的动力学方程表示为二阶皮卡迭代格式后, 一方面, 可以继承皮卡迭代的优点, 使得x(ti)与x(ti+1)彼此独立, 具有并行计算潜力; 另一方面, 可以使得位置量r中显式包含控制量u, 简化后续高斯-牛顿法中雅可比矩阵的求解。
2.2 基于切比雪夫多项式的离散化本节对(11)式所示的连续动力学方程进行离散。相较其他离散化方法, 基于切比雪夫多项式的离散在离散点个数相同时具有更高的精度。根据文献[16-17], 简要概括离散过程为: 将动力学方程由真实时域t∈[t0, tf]转换到虚拟时域τ∈[-1, 1];在每次的迭代过程中, 引入切比雪夫多项式作为基函数, 选择Chebyshev-Gauss-Lobatto(CGL) 点作为配点, 逼近(11)式右端被积函数, 然后逐项积分。上述过程最终可以化简整理为矩阵相乘的形式, 同时, 这一过程也实现了动力学方程的离散。
假设选取N+1个离散点, 定义时间离散序列为τ=[τ0, τ1, …, τN]T, 状态离散序列、控制离散序列分别为X=[x0T, x1T, …, xNT]T, U=[u0T, u1T, …, uNT]T。根据文献[16-17], 动力学方程(11)的离散形式最终可以表示为
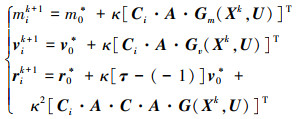
|
(12) |
式中: i=0, 1, …, N为配点序列;k=1, 2, …为迭代次数;κ=(tf-t0)/2为时间转换参数。A = RSTV, T由基函数切比雪夫多项式决定, Ci表示矩阵 C在τi时刻的取值。当离散点个数确定时, C, T, A随即确定为常值矩阵, 这些常数矩阵的具体计算方法在(13)~(17)式给出。Gv(Xk, U), Gm(Xk, U)分别为速度、质量微分方程在各离散点处的取值, 具体为(18)式。

|
(13) |
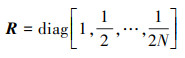
|
(14) |
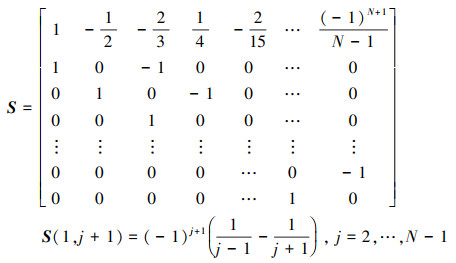
|
(15) |
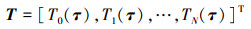
|
(16) |
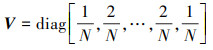
|
(17) |
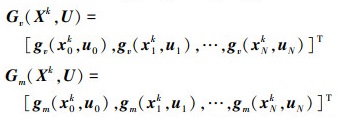
|
(18) |
动力学方程由连续形式转化为离散形式后, 终端时刻的状态即为最后一个离散点处的状态, 则(6)式的轨迹优化问题可以描述为
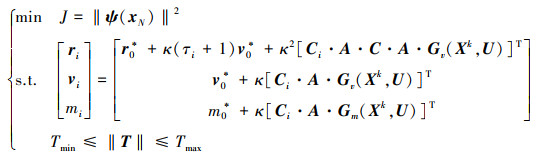
|
(19) |
事实上, 从离散形式的动力学方程可以看出, 状态量x是由控制量u决定的, 则性能指标中的终端状态xN可以由控制序列U表示为
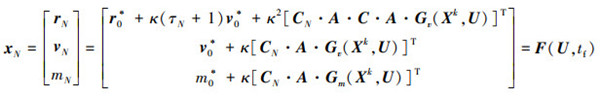
|
(20) |
考虑终端时刻tf自由, 则终端状态xN仅为控制序列U和终端时刻tf的函数。因此, 终端误差最小的轨迹优化问题最终可以表示为

|
(21) |
式中: U∈R3(N+1), tf∈R为待求解变量; Φ(U, tf)= ψ (F(U, tf)): R3N+4→ R6为终端误差关于待求解变量的函数。
因此, 通过二阶皮卡迭代和以切比雪夫为基函数的离散, 将性能指标和动力学方程进行转化, 得到离散后的优化问题如(21)式所示。
2.3 算法框架上文已经将着陆问题最终表示为(21)式, 然后采用高斯-牛顿法求解火箭垂直着陆这一具体问题。
首先不考虑过程中的推力约束, 此时即为非线性最小二乘问题。对于这类问题, 高斯-牛顿法将其转化成一系列线性最小二乘问题迭代求解。高斯-牛顿法的迭代格式为
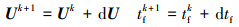
|
(22) |
同时, 在每一次迭代的过程中, 将约束函数Φ在控制变量的初始猜测处泰勒展开, 取其线性项, 以第k次迭代为例
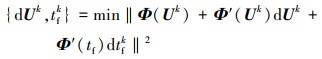
|
(23) |
式中: Φ′(U), Φ′(tf)分别为终端约束关于控制序列U、终端时刻tf的雅可比矩阵, 定义为

|
(24) |
如(23)式所示的线性最小二乘问题中, 待求解变量U, tf的维度高于终端约束函数Φ的维度(3N+4>6), 因此该问题有无穷多解。为了确定其唯一解, 将其构建为最小范数解的优化问题, 即使得待求解变量的迭代步长最小。
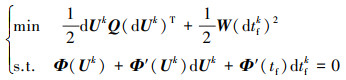
|
(25) |
式中: Q > 0表示控制序列U的权重矩阵;W > 0表示终端时间tf的权重系数。对于(25)式的优化问题, 根据最优化条件推导得到的控制序列及终端时间的显式迭代公式如(26)式所示。
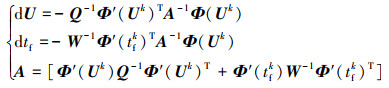
|
(26) |
根据(20)式的动力学方程, 推导可得第k次迭代中的雅可比矩阵为(27)~(28)式。

|
(27) |
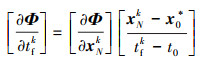
|
(28) |
从前文已知, 推力和气动力均在箭体系表示, 需要借助于ϕ, ψ将其转换到着陆固联系。因此, gv(x, u)的具体表达式为

|
(29) |
式中: Tmax表示推力幅值的最大值。
因此, (27)式中, 雅可比矩阵子矩阵的具体表达式如(30)式所示。
事实上, 从雅可比矩阵计算式(见(27)式)可以看出, 在每一个离散点处雅可比矩阵的子矩阵计算相互独立。上一节中提到, 在已知控制序列的前提下, 各离散点处的状态量也是相互独立的。这也意味着, 这两部分均可以实现同时计算所有离散点处的值。所以, 算法的计算效率会大幅提升。

|
(30) |
对于前文忽略的火箭推力约束, 引入正交投影方法来处理此类边界约束, 提高计算效率。待求解变量在边界处投影后的表达式为
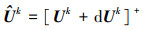
|
(31) |
式中: []+为投影算子, 其定义可以表述为: 对一个要求在[amin, amax]范围内的变量a, [a]+=min(max(a, amin), amax)。对于所选择的控制量, 推力幅值约束实际为调节推力大小节流比η的约束, 即
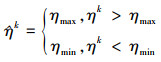
|
(32) |
因此, (32)式可以将推力限制在约束范围内。
综上所述, 对于考虑终端位置、速度约束的火箭一子级着陆非线性最小二乘问题, 通过高斯-牛顿法迭代求解。在此基础上, 采用投影方法约束节流比η。至此, 可以求解得到新的控制序列和新的终端时刻。然后, 基于这一控制序列计算得到状态序列, 判断是否满足收敛条件, 不断迭代直至满足终端收敛条件。根据上述过程, 可以得到待求解变量的显式表达式, 使迭代公式既简洁高效, 又能够处理推力的边界约束, 从而大大提升计算效率, 得到问题的可行解。
2.5 制导策略本文采用如下的闭环制导策略: 在每一个制导周期内首先求解优化问题(25)式得到未来所有时刻的控制量, 插值得到制导指令, 并在当前周期按照此制导指令飞行。到达新的制导周期时, 将当前的状态作为优化初始状态, 上一周期的解作为初始猜想, 求解得到新的控制量, 更新制导指令, 如此循环直到完成着陆任务。
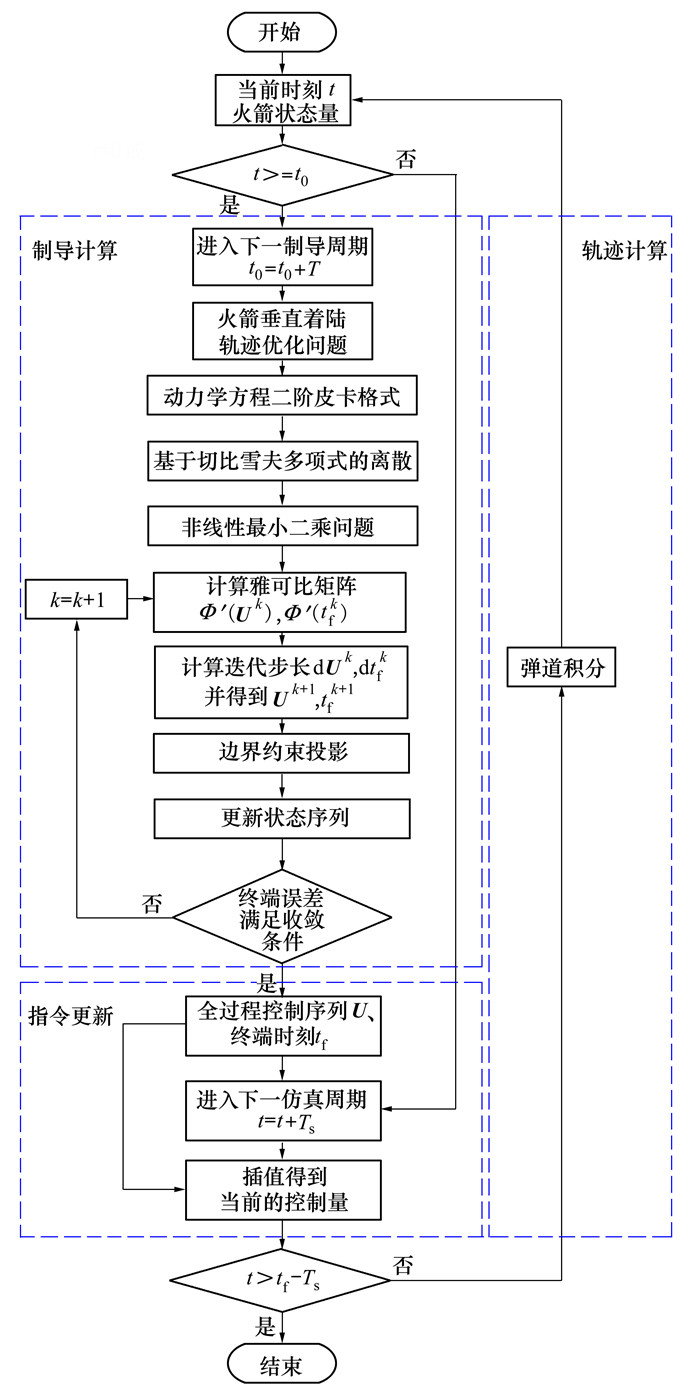
在求解过程中, 限制最大迭代次数来保证计算时间。在有限的迭代次数内不能求解时, 采用上一周期的解来更新制导指令。整个制导方案的过程可以概括为制导计算、指令更新、轨迹计算三部分, 具体方案流程图如图 1所示。图中: T为制导周期, Ts为仿真步长, t0为每一制导周期的初始时刻, tf为终端时刻。
|
| 图 1 火箭子级垂直着陆闭环制导流程图 |
采用文献[11]数值仿真的参数, 具体如表 1~2所示。将终端位置和速度的竖直分量设置为非0(本文中分别设置为1和-1), 实现火箭一子级着陆的终端姿态约束。在计算中, 为了增强数值方法的快速性与稳定性, 采用动力学方程的无量纲模型进行计算。仿真均在配有主频为2.50 GHz的Intel i5-12500H处理器的台式机上执行, 所有程序在MATLAB环境下编制及运行, 序列凸优化算法调用MOSEK求解。
| 参数 | 数值 |
| 初始位置/m | [2 100, 5 582, -450]T |
| 初始速度/(m·s-1) | [-190, -353, 40]T |
| 期望终端位置/m | [0, 1, 0]T |
| 期望终端速度/(m·s-1) | [0, -1, 0]T |
| 参数 | 值 |
| 总质量/t | 38.963 |
| 干质量/t | 27.215 |
| 最大推力/kN | 845.2 |
| 比冲/s | 282 |
| 参考面积/m2 | 10.51 |
| 节流比 | 0~1 |
| 轴向力系数CA | 0.3 |
为了验证二阶皮卡-切比雪夫-牛顿类算法的有效性, 设置30个离散点, 初始猜测设置为线性, 设置位置收敛阈值为1 m, 速度收敛阈值为0.1 m/s。表 3给出了终端时刻的位置、速度等数值, 图 2~4展示了基于二阶皮卡-切比雪夫-牛顿类算法的位置、速度、推力曲线。
| 参数 | 数值 |
| 飞行时间/s | 29.04 |
| 燃料消耗/t | 7.708 0 |
| 终端位置/m | [0.303 0, 1.445 8, -0.063 0]T |
| 终端速度/(m·s-1) | [0.001 1, -0.996 0, -0.000 2]T |

|
| 图 2 位置曲线 |

|
| 图 3 速度曲线 |

|
| 图 4 推力曲线 |
初始时刻优化得到的飞行时间为29.04 s, 燃料消耗为7.708 0 t。通过图 2~3及表 3可以看出, 终端的位置、速度与期望值相比, 均满足要求的收敛阈值1 m和0.1 m/s。由图 4的推力曲线可以看出, 在末端时刻, 推力分量主要在y轴方向, 这也与终端时刻的姿态要求相符。仿真结果表明, 二阶皮卡-切比雪夫-牛顿类算法可以在要求的精度条件下求解火箭垂直着陆的轨迹优化问题。
为了进一步验证二阶皮卡-切比雪夫-牛顿类算法的快速性, 与目前研究较多、收敛速度较快的序列凸优化算法(现有算法)进行对比。目前的序列凸优化算法多以燃料最优为性能指标, 构建SOCP问题进行求解。2.4节提到, 本文的算法处理会使得计算效率大大提高, 其目的在于快速得到一个可行解。因此, 序列凸优化算法以燃料最优为性能指标, 二阶皮卡-切比雪夫-牛顿类算法以迭代步长最短为性能指标, 其余参数与上述相同。
终端误差方面, 分别对2种方法优化结果中的控制序列插值, 然后对原非线性动力学方程采用ode45进行数值积分, 最大步长为0.01 s, 将其积分的终端误差进行对比。如图 5所示, 2种方法的终端误差均呈减小趋势, 而在离散点个数较少时, 本文算法具有更好的表现。

|
| 图 5 终端误差随离散点个数变化曲线 |
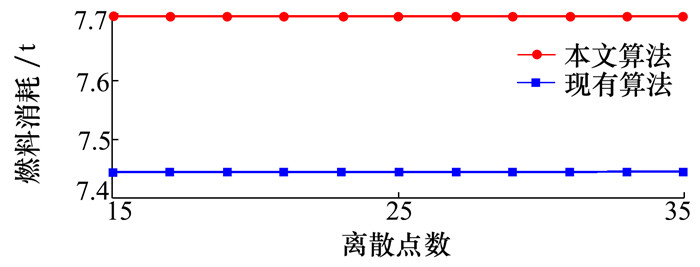
燃料消耗方面, 离散点个数的影响很小。如图 6所示, 现有算法燃料消耗约为7.444 4 t, 本文算法的燃料消耗更多, 约为7.708 0 t, 比现有算法多消耗3.54%。

|
| 图 6 燃料消耗随离散点个数变化曲线 |
计算耗时方面, 统计30次优化求解耗时的平均值进行分析。如图 7所示, 本文算法的计算耗时明显优于现有算法。当离散点数由15增加至35时, 本文算法的平均计算耗时由4 ms增加至10.3 ms, 相较于现有算法, 保持较高的计算效率。
|
| 图 7 计算耗时随离散点个数变化曲线 |
通过上述的结果对比可以说明: 对于火箭一子级垂直着陆的轨迹优化问题, 二阶皮卡-切比雪夫-牛顿类算法可以在较短时间内得到一个可行解。虽然燃料消耗有所增加, 但能够以较高的计算效率得到满足终端精度要求的轨迹。
3.2 闭环制导数值仿真闭环数值仿真中, 设置制导周期为0.1 s, 仿真步长为0.001 s, 同时仿真积分模型增加一阶延时环节(时间常数设置为0.3), 并与开环制导仿真结果进行对比。开环制导, 即只在轨迹初始位置进行一次优化求解, 插值得到后续时刻的制导指令, 代入动力学方程积分得到轨迹。其余参数与表 1~2保持一致。
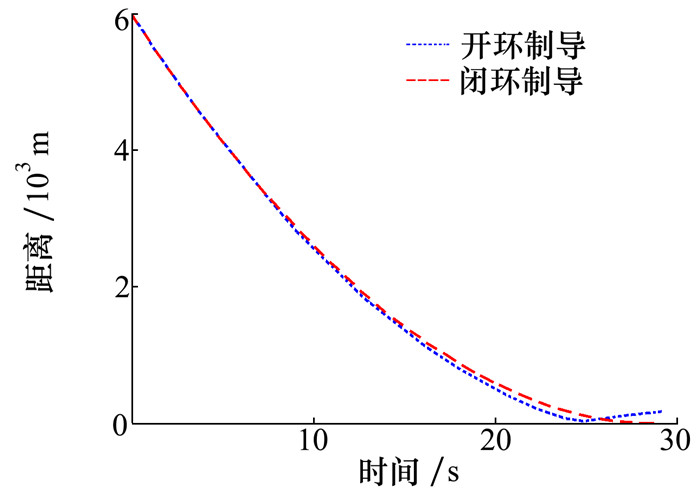
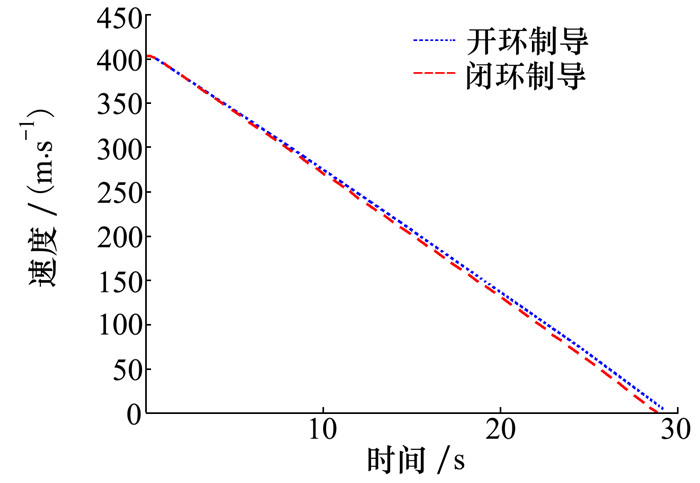
在闭环仿真过程中, 因为后续制导周期以前一制导周期的解作为初始猜测, 所以迭代次数逐渐减小。从图 8~9的闭环仿真曲线可以看出, 开环制导终端的位置、速度有较大误差。闭环制导推力曲线与开环曲线有一定偏差, 这表示在着陆过程中通过不断调整制导指令满足各种约束。闭环仿真结果如表 4所示, 终端位置和速度误差分别为0.000 6 m, 0.003 5 m/s。表 3优化求解得到的终端位置和速度误差分别为0.542 7 m, 0.004 2 m/s。闭环制导与优化求解相比, 终端误差有所减小, 上述的结果共同证明该闭环制导方法是可行的。在终端时刻, 控制量推力矢量方向分别为89°和89.064 7°, 终端时刻推力的x, z轴分量接近于0, 推力分量集中在y轴, 这与终端的姿态要求也是相符的。同时, 无论是火箭的位置、速度曲线, 还是推力曲线, 整个飞行过程中的变化均较为平缓, 具有工程应用潜力。
|
| 图 8 位置曲线 |
|
| 图 9 速度曲线 |

|
| 图 10 推力曲线 |
| 参数 | 数值 |
| 飞行时间/s | 28.789 0 |
| 燃料消耗/t | 7.685 1 |
| 终端位置/m | [-0.000 3, 0.999 5, 0.000 1]T |
| 终端速度/(m·s-1) | [-0.000 6, -0.996 5, -0.000 2]T |
本文提出一种基于二阶皮卡-切比雪夫-牛顿类算法的火箭一子级垂直着陆制导方法。仿真结果表明:
1) 动力学方程基于二阶皮卡迭代格式求解, 可以使得控制量显式表示在状态量中,且各个时刻的状态量相互独立, 二阶皮卡-切比雪夫-牛顿类算法因此具有更高的计算效率。
2) 以二阶皮卡-切比雪夫-牛顿类算法为基础的制导方法, 可以在每个制导周期根据当前状态快速完成规划, 减小累积误差, 制导精度较高。
3) 二阶皮卡-切比雪夫-牛顿类算法通过投影方法处理简单的推力约束, 并没有对推力角、斜坡角等做出约束。对于复杂的过程约束, 算法存在一定的处理难度, 后续需要进一步改进。
| [1] |
王辰, 王小军, 张宏剑, 等. 可重复使用运载火箭发展研究[J]. 飞航导弹, 2018(9): 18-26.
WANG Chen, WANG Xiaojun, ZHANG Hongjian, et al. Research on the development of reusable launch vehicle[J]. Aerodynamic Missile Journal, 2018(9): 18-26. (in Chinese) |
| [2] | LU P. Introducing computational guidance and control[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(2): 193. DOI:10.2514/1.G002745 |
| [3] | SOSTARIC R, REA J. Powered descent guidance methods for the moon and mars[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit, 2005: 6287 |
| [4] |
彭祺擘, 李海阳, 沈红新. 基于高斯-伪谱法的月球定点着陆轨道快速优化设计[J]. 宇航学报, 2010, 31(4): 1012-1016.
PENG Qibo, LI Haiyang, SHEN Hongxin. Rapid lunar exact landing trajectory optimization via Gauss pseudospectral method[J]. Journal of Astronautics, 2010, 31(4): 1012-1016. (in Chinese) |
| [5] | ACIKMESE B, PLOEN S R. Convex programming approach to powered descent guidance for mars landing[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(5): 1353-1366. DOI:10.2514/1.27553 |
| [6] | LIU X. Fuel-optimal rocket landing with aerodynamic controls[J]. Journal of Guidance, Control, and Dynamtcs, 2019, 42(1): 65-77. DOI:10.2514/1.G003537 |
| [7] | SAGLIANO M. Pseudospectral convex optimization for powered descent and landing[J]. Journal of Guidance, Control, and Dynamics, 2017, 41(2): 320-334. |
| [8] |
王劲博, 崔乃刚, 郭继峰, 等. 火箭返回着陆问题高精度快速轨迹优化算法[J]. 控制理论与应用, 2018, 35(3): 389-398.
WANG Jinbo, CUI Naigang, GUO Jifeng, et al. High precision rapid trajectory optimization algorithm for launch vehicle landing[J]. Control Theory and Applications, 2018, 35(3): 389-398. (in Chinese) |
| [9] | SZMUK M, ACIKMESE B, BERNING A W. Successive convexification for fuel-optimal powered landing with aerodynamic drag and non-convex constraints[C]//AIAA Guidance, Navigation, and Control Conference, 2016: 0378 |
| [10] | WANG Z, LU Y. Improved sequential convex programming algorithms for entry trajectory optimization[J]. Journal of Spacecraft and Rockets, 2020, 57(6): 1373-1386. DOI:10.2514/1.A34640 |
| [11] |
张志国, 马英, 耿光有, 等. 火箭垂直回收着陆段在线制导凸优化方法[J]. 弹道学报, 2017, 29(1): 9-16.
ZHANG Zhiguo, MA Ying, GENG Guangyou, et al. Convex optimization method used in the landing-phase online guidance of rocket vertical recovery[J]. Journal of Ballistics, 2017, 29(1): 9-16. (in Chinese) |
| [12] | WANG J, CUI N, WEI C. Optimal rocket landing guidance using convex optimization and model predictive control[J]. Journal of Guidance, Control, and Dynamics, 2019, 42(5): 1078-1092. DOI:10.2514/1.G003518 |
| [13] |
安泽, 熊芬芬, 梁卓楠. 基于偏置比例导引与凸优化的火箭垂直着陆制导[J]. 航空学报, 2020, 41(5): 247-260.
AN Ze, XIONG Fenfen, LIANG Zhuonan. Landing-phase guidance of rocket using bias proportional guidance and convex optimization[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(5): 247-260. (in Chinese) |
| [14] | MA Y, PAN B. Parallel-structured Newton-type guidance by using modified Chebyshev-Picard iteration[J]. Journal of Spacecraft and Rockets, 2020, 58(3): 729-740. |
| [15] | MA Y, PAN B, TANG S. Improved parallel-structured Newton-type guidance for launch vehicles under thrust drop fault[J]. Journal of Spacecraft and Rockets, 2021, 59(2): 467-481. |
| [16] | BAI X, JUNKINS J L. Modified Chebyshev-Picard iteration methods for solution of initial value problems[J]. The Journal of the Astronautical Sciences, 2012, 59(1): 327-351. |
| [17] | JUNKINS J L, BANI YOUNES A, WOOLLANDS R M, et al. Picard iteration, Chebyshev polynomials and Chebyshev-Picard methods: application in astrodynamics[J]. The Journal of the Astronautical Sciences, 2013, 60(3): 623-653. |
2. Shanghai Institute of Aerospace System Engineering, Shanghai 201108, China




