2. 北京理工大学 宇航学院, 北京 100081
对于基于仿真的优化设计, 构建高保真、高可信的数值模拟模型是重中之重。使用与真实结果存在较大差异的数值模拟将造成预测结果不准确, 对于具有高可靠性要求的飞行器而言, 极有可能引入潜在风险, 因此开展飞行器优化设计前必须对数值模拟进行模型确认和可信度评估。然而, 随着所模拟的物理过程日益复杂, 一次性建立适合所有工况的精确仿真模型变得不太现实。比如, 对于计算流体力学(computational fluid dynamics, CFD)数值模拟, 现有研究表明商业或开源CFD软件中模型参数默认值或文献中给出的推荐值并不一定能使一般流动条件下的模型预测效果达到最优[1], 而且机翼表面的压力系数、激波在翼型上表面的位置和激波后压力等对湍流模型封闭系数的变化非常敏感[2]。
传统的模型确认以参数型修正为主, 通过直接在确定性条件下使数值模拟与试验数据之间的偏差最小来实现。该方式直接将模型参数作为修正对象, 物理意义明确, 是目前模型确认研究的主流方向[3]。王纪森等[4]针对油液流动的CFD数值模拟, 采用参数遍历法对Realizable k-ε两方程湍流模型中的参数进行修正, 使得压力损失的仿真结果与试验结果接近。张珍等[5]对雷诺平均方程(Reynolds-averaged Navier-Stokes, RANS)求解中的涡黏系数进行多次修正, 提高了模型对流场各向异性特征预测的性能。
然而, 实际的数值模拟中往往存在大量不确定性, 如CFD数值模拟存在来流和边界条件、湍流模型系数等不确定性, 这对数值模拟输出结果有着不可忽视的影响。例如, 飞行器跨声速飞行时, 流场具有强非线性, 几何外形变化对气动特性影响更加复杂[6]。实际中在不确定性的影响下, 确定性情况下确认好的仿真模型极有可能产生很大的预测偏差, 基于确定性模拟结果得出的结论有可能导致真实系统达不到预期的性能要求, 引入潜在风险。因此, 迫切需要考虑并高效量化不确定性对数值模拟结果的影响, 开展不确定性条件下的模型修正。不确定性量化作为数值模拟模型确认的核心之一, 目前围绕其已经开展了大量研究工作并取得了丰硕的研究成果, 为后续模型修正的开展提供了必要条件。Liu等[7]采用蒙特卡罗仿真(Monte Carlo simulation, MCS)、混沌多项式(polynomial chaos, PC)、径向基函数和梯度增强Kriging等方法研究了跨声速条件下机翼外形加工误差对气动特性的影响, 研究表明, 梯度增强的降阶模型方法效率更高。Loeven等[8]通过对参数化建模后的机翼使用概率配置点法, 研究了翼型的厚度、最大弯度位置和最大弯度等关键设计变量的不确定性对翼型气动特性的影响。Geneva等[9]采用深度学习技术对RANS方程中的模型不确定性进行量化, 并提供了诸如速度和压力等输出的概率区间。陈江涛等[10]使用混沌多项式方法研究了湍流模型系数的不确定度对RAE2822跨声速翼型绕流模拟的影响, 计算中关注了数值模拟的积分量(升力系数和阻力系数)和局部量(壁面压力、摩擦因数和空间马赫分布)的不确定度量化结果。
综上可见, 目前围绕数值模拟的模型确认, 大量的研究工作均未考虑模拟中的不确定性。虽然目前已开展了很多CFD不确定性量化的研究工作, 这些工作为梳理各类不确定性对流动特性的影响规律及其大小提供了丰富的思路, 给后续CFD数值模拟的模型修正工作的开展奠定了良好的基础。但是, 面对实际中的高维不确定性, 不确定性量化面临“维数灾难”难题。同时, 如何基于不确定性量化的结果进行高效的模型参数修正, 构建高可信的预测模型, 打破传统依赖经验或试凑的低效模型确认模式, 形成不确定性下数值模拟模型确认的闭环流程, 还较少有研究报道。因此, 本文提出一套集不确定性量化、灵敏度分析、确认度量、参数修正为一体的考虑不确定性的数值模拟模型确认流程, 并将提出的方法应用于NACA0012和ONERA M6翼型的CFD数值模拟模型确认。
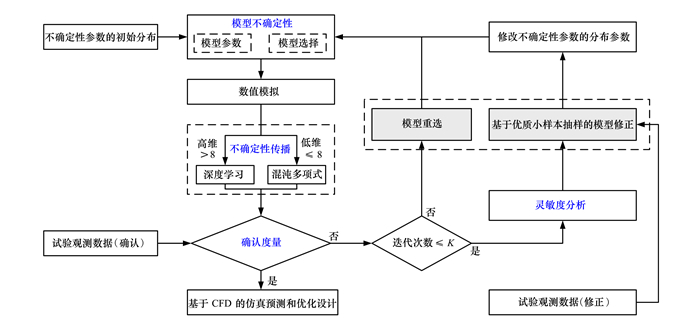
1 基于优质小样本的模型确认方法为提高数值模拟的可信度和预测能力, 为后续开展分析和优化设计提供高保真的仿真模型, 本文提出一种集不确定性量化、灵敏度分析、确认度量、参数修正为一体的数值模拟模型确认方法。图 1展示了所提出方法的实施流程, 其具体实现步骤如下。
|
| 图 1 提出的模型确认方法流程图 |
步骤1 初始数值模拟模型构建, 确定不确定性参数分布类型及其分布参数。
确定数值模拟的边界条件等, 确定数值模拟仿真模型及模型参数的不确定性分布类型和分布参数, 如CFD数值模型中的湍流模型及其封闭系数。
步骤2 不确定性量化, 得到不确定性影响下数值模拟输出响应的不确定性。
基于给定的不确定性分布信息, 对数值模拟的输出响应进行不确定性量化, 针对低维问题(≤8维)推荐使用混沌多项式方法(见1.1.1小节), 针对高维问题(>8维)采用深度学习方法(见1.1.2小节)。上述维度划分是基于文献[11-12]中的定义以及对混沌多项式与深度学习的特性和使用习惯经测试后得到的。
步骤3 结合试验数据进行数值模拟模型的确认度量(见1.2小节), 若模型不满足要求(即: 确认度量指标>ε), 则进入步骤4, 否则模型确认程序结束, 可基于当前数值模拟模型进行后续的仿真分析和优化设计。
步骤4 全局灵敏度分析, 发掘重要的修正参数。
应用全局灵敏度分析方法(见1.3小节)量化模型参数对输出响应的重要程度, 并进行重要性排序, 从中选取影响较大的参数进行后续修正。
步骤5 基于优质小样本的参数修正或模型重选。
通过结合试验数据并应用优质小样本方法(见1.4小节)选择与试验数据更加吻合的数值模拟样本, 并逆向反推得到相应的不确定性模型参数分布范围或分布参数, 实现参数修正。若参数修正迭代次数大于给定阈值K时仍无法获取满足确认度量准则的数值模拟, 则可进行模型重选, 例如对于CFD数值模拟, 可选择最佳的湍流模型。利用贝叶斯定理计算各个候选模型的后验分布, 选择与试验数据更吻合的模型。也可采用贝叶斯平均方法对多个候选模型进行融合, 共同实现响应预测。
步骤6 重复步骤2~5, 直至确认度量指标满足要求(EMR≤ε), 则可利用最新的数值模拟模型进行分析和优化设计。
1.1 不确定性量化方法从图 1中可以发现, 不确定性传播是必不可少的环节, 它在整个模型确认流程中起着举足轻重的作用。不确定性传播的方法有很多, 如蒙特卡罗仿真(Monte Carlo simulation, MCS)、混沌多项式(polynomial chaos, PC)和深度学习(deep learning, DL)等。PC方法理论完备且具有指数收敛速度, 近年来在数值模拟的不确定性量化和优化设计中得到广泛研究和应用[13]。但PC方法在非线性极强的高维问题上容易出现收敛缓慢甚至无法收敛的问题。而深度学习(deep learning, DL)技术由于其对复杂高维函数具有较强的表征能力, 越来越多的复杂工程问题可通过深度学习得以解决[14]。深度学习技术的应用, 相当于构建了高维函数的代理模型, 不确定性量化则在代理模型上进行, 为突破高维不确定性量化的“维数灾难”提供了有效解决途径。因此在本节中介绍应用最为广泛的PC方法和深度学习方法。
1.1.1 基于混沌多项式的不确定性量化
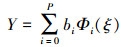
|
(1) |
式中:ξ为标准随机变量;b为PC系数, 正交多项式Φi(ξ)是各维随机分布对应的一维正交多项式的乘积, 即
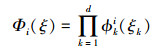
|
(2) |
式中,ϕki(ξk)表示第k维随机变量ξk所对应的一维正交多项式。对多项式Φ(ξ)的p阶截断, Φi(ξ)的最高阶次不超过p阶。
本文采用随机响应面法(stochastic response surface method, SRSM)求解PC系数, 将标准随机样本ξS和相应的真实函数响应值 G代入(2)式中PC模型两端, 得
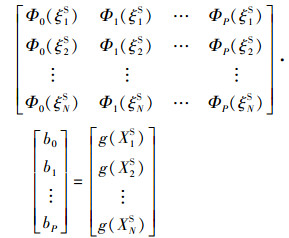
|
(3) |
(3) 式可简写为
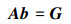
|
(4) |
基于(4)式, 利用最小二乘法计算PC系数。
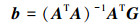
|
(5) |
当得到PC系数后, 可用解析表达式(6)~(7)非常方便地计算输出响应y的前两阶统计矩。
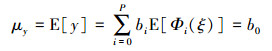
|
(6) |
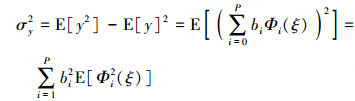
|
(7) |
贝叶斯深度神经网络(Bayesian neural networks, BNN)作为深度神经网络的一个分支, 具有稳健性高且能避免过拟合问题的优势[17]。
对于一个具体问题来说, 当给定d维输入向量 x, 可定义一个具有L层的深度神经网络
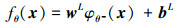
|
(8) |
式中:wL和 bL是网络第L层(即输出层)的权值和偏差; φθ-(x)是输入变量 x经前L-1层网络运算后的迭代值; θ-表示前L-1层全部的网络参数; fθ表示最后得到的网络参数为 θ的深度神经网络。
在一般的深度学习中, w和b都是确定的值, 贝叶斯网络为了提高网络的稳健性, 认为权值和偏差由确定的值变成服从某种概率分布。本文在普通全连接神经网络的基础上, 仅将输出层设定为贝叶斯层, 同时假设输出层无偏差, 以此作为贝叶斯深度神经网络的基本结构, 在此基础上构建深度神经网络[18]。对于一个已经训练好的贝叶斯深度神经网络, w表示输出层的权值, 通常认为服从正态分布[19], 即: w~N(μw, σw2), θ-表示其他层的参数, 则BNN可表示如下
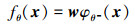
|
(9) |
式中, φθ-(x)是倒数第二层的输出向量。由于神经网络的计算速度极快, 可通过直接在BNN上运行MCS的方法进行不确定性量化。
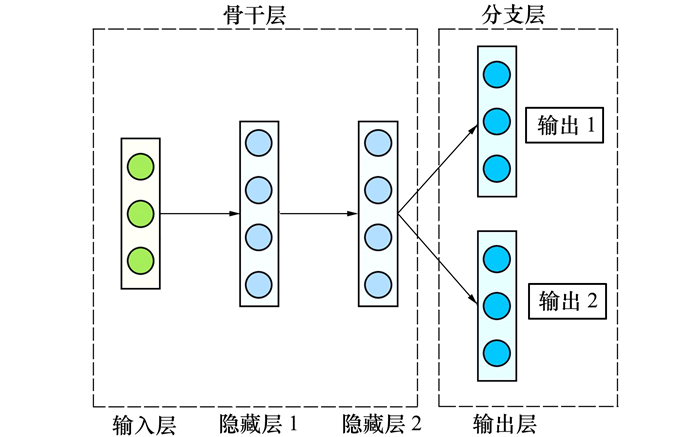
多分支网络可以更好地应对存在相关性的多输入和多输出问题, 其分支层可以根据问题的不同构建在输入层或输出层处。图 2展示了一个有2层隐藏层的多分支神经网络结构图, 其中输入层与前2层隐藏层为骨干层, 输出层为分支层。
|
| 图 2 多分支神经网络结构 |
通常情况下由于试验数据获取成本非常昂贵, 往往仅能得到少量几个试验数据, 此时可采用基于距离的确认度量指标, 具体介绍如下。
获得相同输出响应量的ne个试验测量样本 ye=[y1e, …, ynee], 进一步地引入“距离”这一概念来描述试验测量数据 ye与数值模拟结果 ya之间的差异进行模型确认工作, 即判断数值模拟是否满足精度需求。相应的距离指标设为平均相对误差EMR。
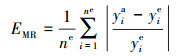
|
(10) |
式中, yia为相应的基于数值模拟得到输出响应值, 可通过步骤2中的不确定性量化获得。
如果存在若干个不同的工况需要同时进行模型确认, 则可对多个工况下的EMR累加求和, 作为模型确认度量的指标。
除此之外, 若获取到的试验数据较多(ne较大), 可有效构建输出响应的经验概率分布模型, 则可采用面积法(Area Metric, AM)作为确认度量准则[20], 其计算公式如下。
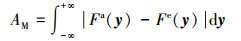
|
(11) |
式中:y为数值模拟的输出响应;Fa(y)为根据数值模拟所得输出样本所构建的 y累积分布函数(cumulative distribution function, CDF); Fe(y)为根据试验测量样本 ye所构建的 y的经验累积分布函数(empirical cumulative distribution function, ECDF)。
1.3 全局灵敏度分析基于不确定性量化的结果, 开展全局灵敏度分析。传统的处理随机不确定性的全局灵敏度分析方法大体可以分为基于回归的方法和基于方差的方法[21], 其中基于全局灵敏度指标的方差分析法因其简单有效的特点得到了确认应用。对于一个有着d维输入向量 x =[x1, …, xd]的随机响应函数y=g(x), 其方差D可以表示为
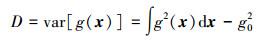
|
(12) |
式中, g0表示 y的均值。
进一步, (12)式可以分解为
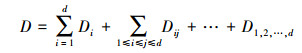
|
(13) |
式中, Di=∫gi2(xi)dxi表示相应维度单一变量对输出的影响, Di1, …, is=∫gii, …, is2(xi1, …, xis)d(xi1, …, xis)输入变量间的交互作用对输出的影响。
因此, 全局指数定义为
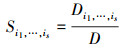
|
(14) |
基于(14)式, 有以下特性
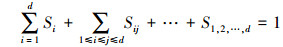
|
(15) |
由于在不确定性量化中采用PC和深度学习方法, 二者都相当于构建了数值模拟响应预测的一个随机代理模型, 计算非常快, 因此灵敏度分析结合MCS可非常便捷地快速执行。考虑到混沌多项式方法将随机输出响应表示为一组正交多项式的加权组合, 因此可解析地得到响应的方差(见1.1.1小节), 从而非常方便地得到全局灵敏度指标的解析表达。相比于MCS, 该方法可进一步减少计算资源消耗。
全局灵敏度指标可表示为
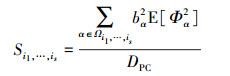
|
(16) |
式中, DPC为总方差, 可通过(7)式计算得到。
1.4 基于优质小样本的模型参数修正若步骤3中进行确认度量后, 数值模拟模型不满足要求, 则基于当前参数得到数值模拟响应输出的na个样本, 由于采用PC或深度学习进行不确定性传播和量化, 该过程不耗费任何函数调用, na可以设置得很大。从na个数值模拟输出样本中挑选出距离试验数据 ye最近的一定数目的样本, 将部分样本称作优质小样本, 设置一定的截断比率r
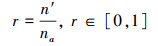
|
(17) |
式中, n′为优质小样本的样本数目。
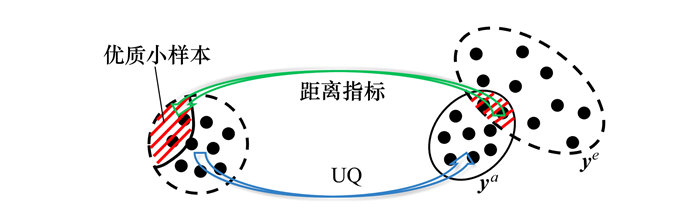
截断比率r需要在模型确认开始之前定义。它主要用于控制模型确认迭代过程的收敛速度, 其大小取决于初始数值模拟数据与试验数据的差异程度。一般来说, r取值越大, 每次截取的优质小样本的容量越大, 则修正过程收敛越慢, 从而需要更多的迭代步数; r取值越小, 则修正过程收敛速度越快, 但有可能导致最后修正精度不足。同时, 收敛速度也与待修正参数的数量有关, 待修正的参数越多, 收敛速度越慢。基于作者的经验, 建议在一次修正过程中同时修正的参数不超过3个, 截断比率r取0.05~0.3。基于优质小样本的模型参数修正方法其原理如图 3所示, 通过反推找出每个优质小样本相对应的输入参数样本, 基于所有优质小样本对应的输入, 结合模型参数的分布类型更新分布参数, 如均匀分布的上下界、正态分布的均值和方差等。度量指标ε也是该方法的重要参数之一, ε的值取决于用户对模型确认精度的需求, 更高的精度需要更长的收敛过程。基于作者经验, 建议度量指标ε < 0.05。
|
| 图 3 基于优质小样本的参数修正原理示意 |
本节将考虑湍流模型系数存在不确定性, 将提出的数值模拟模型确认闭环流程应用于NACA0012翼型的CFD模型确认, 提升CFD气动预测数据与试验数据的一致性。在本节中, 模型确认问题中的截断比率取r=0.1, 确认度量采用MRE方法, 度量指标取ε=0.01。
本算例选取SA湍流模型[22]进行CFD数值模拟, 考虑其中的6个封闭系数存在不确定性并进行修正, 认为其在变化范围内服从均匀分布。利用ICEM软件生成计算用网格, 在空气动力学分析中, 使用Fluent 19.0作为CFD求解器, 电脑配置为16 G内存, 显卡为NVIDIA 1660, CPU为Intel(R) Core(TM) i5-9400F。
考虑进行模型确认的流动条件为Ma=0.15和Re=6×106, 且存在攻角α为0°, 2°, 4°, 6°, 8°, 10°和11°多种工况。模型确认中进行确认度量和参数修正所用到的升力系数试验数据来源于NASA网站的公开数据[23]。在给定模型封闭系数初始分布时, 若封闭系数的初始区间设置较大, 在这个区间对封闭系数取值进行CFD数值模拟, 得到的输出响应上下边界范围内一定可以包含试验数据, 也就是说当前流动情况下的模型系数最佳值一定包含在初始区间内。但很多情况下, 给定的初始区间很可能较小且极有可能偏离最佳参数范围。为了较为全面地验证所提出的模型确认方法的有效性, 考虑2种情况进行测试:
情况1 封闭系数的初始范围较大, 封闭系数在其变化区间内服从均匀分布, 其变化范围见表 1。
| 系数 | Cb1 | Cb2 | Cv1 | Cw2 | Cw3 | σ |
| 最小值 | 0.067 8 | 0.311 0 | 3.55 | 0.15 | 1.0 | 0.333 5 |
| 最大值 | 0.203 3 | 0.933 0 | 10.65 | 0.45 | 3.0 | 1.000 5 |
| 默认值 | 0.135 5 | 0.622 0 | 7.10 | 0.30 | 2.0 | 0.667 0 |
情况2 封闭系数的初始范围较小, 假设湍流模型系数在默认值处服从±10%的均匀分布, 默认值见表 1。
针对以上2种情况所采取的模型确认策略也有所不同。对于情况1, 由于封闭系数的初始不确定性极大, 在模型确认过程中需要降低其不确定性, 即维持其分布类型不变并减小封闭系数的变化区间; 对于情况2, 封闭系数的初始不确定性较小, 但是极有可能处在不合适的区域, 因此模型确认需要调整其范围, 即维持其分布类型不变并修正均值。
首先, 对NACA0012基准翼型在名义流动条件下(α=10°, Ma=0.15, Re=6×106)进行了网格收敛测试, 避免网格带来的气动预测不确定性, 在测试中湍流模型选择SA, 模型系数取表 2所示的默认值。网格收敛性测试的结果见表 2, 从中可以看出, 当网格密度增加到一定数值时(远场: 150;翼型边界: 300), 升力系数几乎没有变化。因此, 在本小节的CFD模拟中, 网格远场的节点数被设定为150, 而翼型边界的节点数被设定为300。同时, 对比该工况下的升力系数试验数据(1.080 9), 可以发现基于CFD仿真得到的升力系数存在7%左右的误差, 也证明了对CFD进行模型确认的必要性。
| 网格密度 | 升力系数 | 仿真时间/s | |
| 远场 | 翼型边界 | ||
| 80 | 160 | 0.784 3 | 148.860 1 |
| 100 | 200 | 0.865 7 | 186.276 0 |
| 120 | 240 | 0.921 4 | 236.069 9 |
| 150 | 300 | 0.995 0 | 291.044 9 |
| 180 | 360 | 0.995 0 | 351.966 1 |
利用混沌多项式(PC)方法进行不确定性量化, 构建以6个湍流模型封闭系数为输入、升力系数为输出的2阶PC模型, 并利用最小二次回归方法计算PC系数。
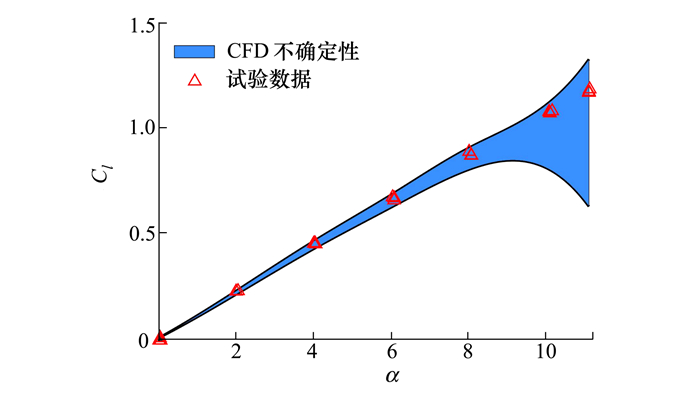
2.1 情况1基于湍流系数的分布类型和初始分布参数进行第一次UQ, 获得CFD数值模拟输出响应的取值范围, 即升力系数的不确定性区间。UQ的结果如图 4所示, 从中可以看出初始阶段CFD预测的升力系数的不确定度(图中蓝色区域面积)较大, 尤其在大攻角范围(>10°)非常明显, 同时可以计算得到此时的最大EMR为0.43, 明显不满足精度要求且远超容忍值(ε=5%), 因此需要开展参数修正。
|
| 图 4 初始阶段CFD不确定性量化的结果(情况1) |
为了降低参数修正的难度, 提高收敛速度, 首先采用1.3节介绍的方法对升力系数进行全局灵敏度分析, 查找对升力系数影响最大的湍流模型系数, 各个封闭系数的全局指数如表 3所示。从表中可以看出, 对于这7种工况, Cb1对升力系数的影响最大, 且都远大于其他几个封闭系数。因此, 仅对Cb1进行参数修正, 此时其他系数固定在默认值处。
| 攻角/(°) | Cb1 | Cb2 | Cv1 | Cw2 | Cw3 | σ |
| 0 | 72.74 | 1.08 | 10.32 | 0.38 | 15.41 | 0.00 |
| 2 | 61.39 | 3.17 | 15.41 | 0.07 | 19.16 | 0.79 |
| 4 | 65.86 | 2.15 | 15.31 | 0.07 | 15.39 | 1.20 |
| 6 | 60.47 | 0.97 | 18.27 | 0.13 | 20.01 | 0.13 |
| 8 | 86.97 | 4.86 | 2.16 | 0.24 | 5.37 | 0.08 |
| 10 | 86.69 | 3.48 | 1.57 | 7.86 | 0.22 | 0.17 |
| 11 | 89.79 | 2.15 | 3.21 | 0.44 | 1.42 | 2.99 |
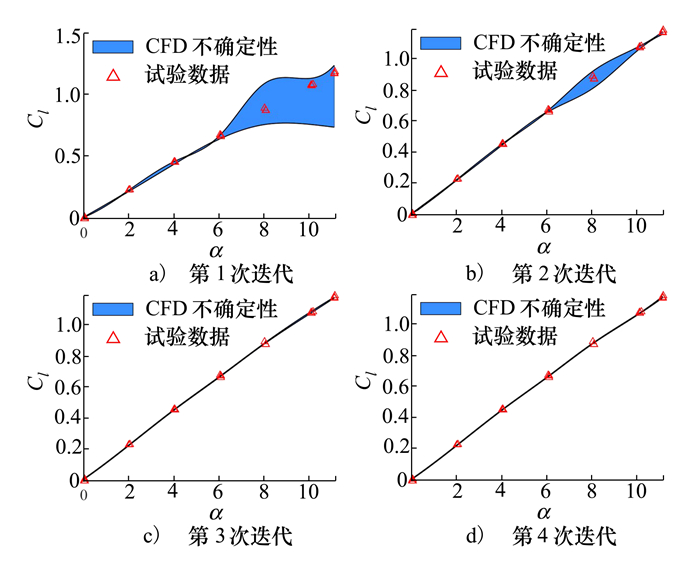
CFD参数修正过程中的升力系数的不确定性区间见图 5中蓝色部分。随着修正过程的不断迭代, 对封闭系数不断修正, 相当于封闭系数取值的认知不确定性逐步减少, 则升力系数的不确定度也随之逐渐降低(即图片中蓝色区域逐渐缩小), 最终CFD仿真的结果与试验数据十分吻合, 完成模型确认。
|
| 图 5 参数修正CFD升力系数预测区间和试验数据(情况1) |
Cb1的确认结果展示在表 4中, 从中可以发现经模型确认后Cb1的变化范围中并非包含默认值(0.135 5), 对Cb1的变化区间取中值, 显然与默认值略有不同。这也印证了文献[1]中的观点, 按照湍流模型给定的默认系数, CFD仿真结果并非与试验数据高度吻合。
| 迭代 | 区间 | 迭代 | 区间 | |
| 0 | [0.067 8, 0.203 3] | 3 | [0.143 6, 0.144 0] | |
| 1 | [0.122 8, 0.166 3] | 4 | [0.143 6, 0.144 0] | |
| 2 | [0.141 6, 0.145 7] |
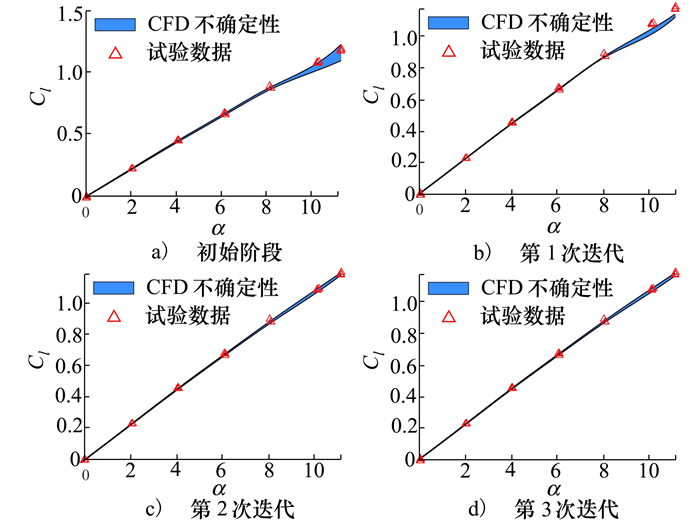
首先进行初始状态的UQ, 结果展示于图 6a)。
|
| 图 6 参数修正CFD升力系数预测区间和试验数据(情况2) |
从图中可以看出, 初始状态下的CFD预测的升力系数不确定性区间并没有很好地覆盖试验数据。基于表 3得知, 对升力系数影响最大的都是Cb1, 因此仅对Cb1进行修正, 其他系数固定在默认值处。
CFD参数修正过程中的升力系数不确定性区间见图 6中蓝色部分。随着修正过程的不断迭代, CFD不确定性区间逐渐向上偏移, 最终能完全覆盖试验数据。
Cb1的确认结果展示于表 5中, 可以发现经确认后Cb1的取值与表 4中的结果高度吻合, 这也再一次验证了所提出方法的有效性。
| 迭代 | 区间 | 取值 | 迭代 | 区间 | 取值 | |
| 0 | [0.121 9, 0.149 1] | 0.135 5 | 2 | [0.129 1, 0.157 7] | 0.143 4 | |
| 1 | [0122 8, 0150 2] | 0.136 5 | 3 | [0.129 2, 0.157 9] | 0.143 6 |
本文针对数值模拟模型确认, 提出了一种考虑不确定性的数值模拟模型确认方法, 并通过NACA0012翼型CFD数值模拟的模型确认应用, 验证了提出的数值模拟模型确认闭环流程的有效性。研究表明, 该方法有如下优势:
1) 建立一套涵括不确定性量化、全局灵敏度分析、参数修正、确认度量的模型确认闭环流程, 可以合理有效地降低数值模拟中的不确定性;
2) 利用全局灵敏度分析筛选对输出影响较大的模型参数, 有效降低了模型确认的计算量;
3) 建立一种基于优质小样本的模型参数修正策略, 选取部分优质小样本实现反向不确定性量化, 从而快速有效地实现模型参数修正;
4) 提出的方法丰富了目前不确定性下的数值模拟模型确认理论和规范, 为建立高可信度的学科或系统仿真分析模型提供了科学系统的方法, 为后续开展飞行器稳健优化设计提供高保真的分析模型;
5) 提出的方法通过将模型看作一个黑箱问题, 仅关注待修正参数和输出的关系, 极大地降低了模型确认的难度, 并能够推广至工程应用中的各种模型确认问题。
| [1] | MARGHERI L, MELDI M, SALVETTI M V, et al. Epistemic uncertainties in rans model free coefficients[J]. Computers and Fluids, 2014, 102(10): 315-335. |
| [2] | XIAO H, CINNELLA P. Quantification of model uncertainty in RANS simulations: a review[J]. Progress in Aerospace Sciences, 2019, 108: 1-31. DOI:10.1016/j.paerosci.2018.10.001 |
| [3] | XU H, QIN D, LIU C, et al. An improved dynamic model updating method for multistage gearbox based on surrogate model and sensitivity analysis[J]. IEEE Access, 2021, 9: 18527-18537. DOI:10.1109/ACCESS.2021.3053395 |
| [4] |
王纪森, 贾倩, 陈晨, 等. 液压管路油液流动的湍流模型参数修正研究[J]. 系统仿真学报, 2018, 30(5): 1665-1671.
WANG Jisen, JIA Qian, CHEN Chen, et al. Research of turbulence model parameters correction for oil flow of pipeline[J]. Journal of System Simulation, 2018, 30(5): 1665-1671. (in Chinese) |
| [5] |
张珍, 叶舒然, 岳杰顺, 等. 基于组合神经网络的雷诺平均湍流模型多次修正方法[J]. 力学学报, 2021, 53(6): 1532-1542.
ZHANG Zhen, YE Shuran, YUE Jieshun, et al. A combined neural network and multiple modification strategy for Reynolds-averaged Navier-Stokes turbulence modeling[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(6): 1532-1542. (in Chinese) |
| [6] | CINNELLA P, DWIGHT R, EDELING W. Review of uncertainty quantification in turbulence modelling to date[C]//SIAM Uncertainty Quantification Conference, Switzerland, 2016 |
| [7] | LIU D S, LITVINENKO A, SCHILLINGS C, et al. Quantification of airfoil geometry-induced aerodynamic uncertainties-comparison of approaches[J]. SIAM/ASA Journal on Uncertainty Quantification, 2017, 5(1): 334-352. DOI:10.1137/15M1050239 |
| [8] | LOEVEN A, BIJL H. Airfoil analysis with uncertain geometry using the probabilistic collocation method[C]//49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Schaumburg, 2008 |
| [9] | GENEVA N, ZABARAS N. Quantifying model form uncertainty in Reynolds-averaged turbulence models with Bayesian deep neural networks[J]. Journal of Computational Physics, 2019, 383: 125-147. DOI:10.1016/j.jcp.2019.01.021 |
| [10] | CHEN J, ZHANG C, ZHAO W, et al. A high-fidelity polynomial chaos modified method suitable for CFD uncertainty quantification[C]//Journal of Physics, 2021, 1985(1): 012042 |
| [11] | SIMPSON T, TOROPOV V, BALABANOV V, et al. Design and analysis of computer experiments in multidisciplinary design optimization: a review of how far we have come-or not[C]//12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, 2008 |
| [12] | SHAN S Q, WANG G G. Metamodeling for high dimensional simulation-based design problems[J]. Journal of Mechanical Design, 2010, 132(5): 11. |
| [13] | XIU D, KARNIADAKIS G E. Modeling uncertainty in flow simulations via generalized polynomial chaos[J]. Journal of Computational Physics, 2003, 187(1): 137-167. DOI:10.1016/S0021-9991(03)00092-5 |
| [14] |
陈海, 钱炜祺, 何磊. 基于深度学习的翼型气动系数预测[J]. 空气动力学学报, 2018, 36(2): 294-299.
CHEN Hai, QIAN Weiqi, HE Lei. Aerodynamic coefficient prediction of airfoils based on deep learning[J]. Acta Aerodynamica Sinica, 2018, 36(2): 294-299. (in Chinese) |
| [15] |
熊芬芬, 杨树兴, 刘宇, 等. 工程概率不确定性分析方法[M]. 北京: 科学出版社, 2015.
XIONG Fenfen, YANG Shuxing, LIU Yu, et al. Engineering probabilistic uncertainty analysis method[M]. Beijing: Science Press, 2015. (in Chinese) |
| [16] |
熊芬芬, 陈江涛, 任成坤, 等. 不确定性量化的混沌多项式方法研究进展[J]. 中国舰船研究, 2021, 16(4): 18.
XIONG Fenfen, CHEN Jiangtao, REN Chengkun, et al. Recent advances in polynomial chaos method for uncertainty propagation[J]. Chinese Journal of Ship Research, 2021, 16(4): 18. (in Chinese) |
| [17] | WANG H, YEUNG D Y. A survey on Bayesian deep learning[J]. ACM Computing Surveys, 2020, 53(5): 1-37. |
| [18] | BLUNDELL C, CORNEBISE J, KAVUKCUOGLU K, et al. Weight uncertainty in neural network[C]//International Conference on Machine Learning, 2015: 1613-1622 |
| [19] | SNOEK J, RIPPEL O, SWERSKY K, et al. Scalable Bayesian optimization using deep neural networks[C]//International Conference on Machine Learning, 2015: 2171-2180 |
| [20] | LIU Y, CHEN W, ARENDT P, et al. Toward a better understanding of model validation metrics[J]. Journal of Mechanical Design, 2011, 133(7): 071005. |
| [21] | SUDRET B. Global sensitivity analysis using polynomial chaos expansions[J]. Reliability Engineering & System Safety, 2008, 93(7): 964-979. |
| [22] | HE X, ZHAO F, VAHDATI M. Uncertainty quantification of spalart-allmaras turbulence model coefficients for simplified compressor flow features[J]. Journal of Fluids Engineering, 2019, 142(9): 36-48. |
| [23] | LADSON C L, HILL A S, JOHNSON JR W G. Pressure distributions from high Reynolds number transonic tests of an NACA 0012 airfoil in the Langley 0.3-meter transonic cryogenic tunnel[R]. NASA-TM-100527, 1987 |
2. School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China




