滚动轴承是常见且用途广泛的一类机械器件。然而,滚动轴承常常工作于高温、高速和重载的复杂服役环境,导致其关键构件故障时有发生。因此,进行早期异常检测和故障诊断对保障滚动轴承的安全运行至关重要。
数据驱动的智能故障诊断方法通常分为3个步骤:振动信号采集、故障特征提取和模式识别。其中,故障特征提取的准确程度直接影响到分类结果。有许多特征提取算法已经得到了广泛的应用,如时频域特征、基于复杂度的特征、基于人工智能算法提取的特征等[1]。由于工作环境复杂、滚动体的非线性刚度等因素,旋转机械的振动信号通常是非线性、非平稳的。
然而,在旋转机械诊断过程中,为线性信号设计的传统时域和频域特征提取技术总是难以提取到有效特征[2]。此时,表现信号复杂程度的非线性信号定量描述方法逐渐进入研究人员的视野[3]。熵可以测量时间序列的无序程度,因此它可以反映出旋转机械发生故障时系统动力学的突变行为[4-5]。Kolmogorov在1958年提出了K-S熵,用于描述一个系统的复杂性[6]。Pincus在K-S熵的基础上上提出了近似熵(ApEn),这种算法通过考虑时间序列中生成新信息的速度来衡量信号的复杂性[7]。之后,Richman和Moorman提出样本熵(SE),以解决ApEn中的自匹配问题[8]。Chen等将模糊隶属度函数引入样本熵,并提出了更准确的模糊熵(FE)[9]。此外,一些研究人员将时间序列符号化以观察信号的变化,如排列熵(PE)和符号动力学熵(SDE)[10-11]。符号动力学熵将振动加速度信号符号化处理,通过比对信号在相空间中的排列模式和产生新模式的概率衡量信号复杂度,具有良好的抗噪性和计算效率。
结合Costa提出的多尺度思想,Li等提出了多尺度符号动力学熵(MSDE),它可以提取振动信号中不同尺度下蕴含的信息[11-12]。现在得到广泛应用的熵值方法仅有特征提取功能,这需要大量的标记数据来训练智能模型进行分类。上述基于熵的方法适用于处理具有相同分布的训练和测试数据。这意味着需要在诊断前获取大量同分布的数据。但是,在实际生产应用当中获取此类数据存在许多困难:
1) 设备不允许在故障状态下长时间运行,这使得很难获得大量故障数据。
2) 设备可能仅因一种类型的故障而出现故障,难以收集到所有类型的故障数据。
3) 不可能对要诊断的每个设备实施模拟。
因此,在现实世界中,很难获得足够的标记数据来训练模型。模型只能使用不符合同分布假设的数据进行训练。这就是本文重点关注的跨域故障诊断问题。
为了解决这个问题,许多研究人员试图进一步对特征进行数学变换,以减少训练数据和测试数据之间的分布差异,然后将变换后的特征输入分类器。这就是基于特征的迁移学习算法的思路。例如,Pan和Yang等提出的最大均值差异嵌入(MMDE)算法[13-14]、在此基础上发展出的迁移成分分析(TCA)方法[15]、Zheng等于2017年提出迁移局部保持投影(TLPPIFI)算法[16]等。这些迁移学习方法降低了变换后特征的最大均值差异(MMD),使得通过不同分布的数据来识别故障类型成为可能[17]。
1 多尺度迁移符号动力学熵(MTSDE)本文方法的主要思想是在提取振动信号的MSDE特征后,构建一个降维投影矩阵,将源域和目标域的MSDE特征投影到一个子空间中,使得具有相同类别的样本更加聚类。
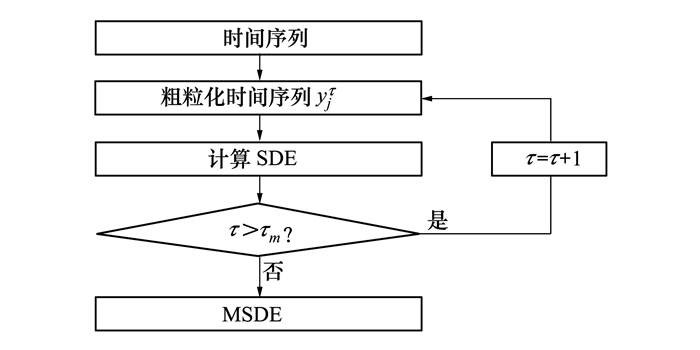
1.1 提取符号动力学熵特征MSDE能够在不同的尺度下提取滚动轴承的故障信息,同时还具有较好的抗噪性和较高的计算效率。根据文献[11],计算方法如下:
1) 给定时间序列{Xi}={x1, x2, …, xn}, 粗粒化分割得到尺度为τ的时间序列{yjτ}
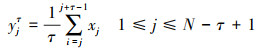
|
(1) |
式中,τ为尺度, 且为正整数, 通过调节其值可得不同尺度的时间序列。
2) 计算{yjτ}的多尺度符号动力学熵MSDE[1]
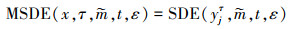
|
(2) |
式中,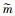

|
(3) |
式中,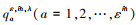
|
| 图 1 MSDE的计算流程 |
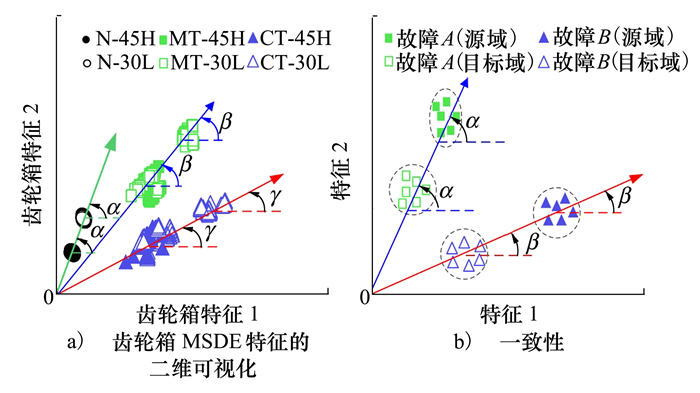
传统的基于MSDE的智能故障诊断模型需要大量的标记数据来训练分类器。但是, 在实际生产中通常难以收集到足够标记的数据。如果模型建立在标记样本不足的基础上, 诊断性能将显著退化。在迁移学习技术的帮助下, 在同类型设备上收集的数据可以被用于训练模型, 以实现对目标机器的故障诊断。为了实现迁移学习策略, 有必要找出收集自同类型不同设备上的数据之间的相似性。本文提取了一组从齿轮箱收集到的振动数据的MSDE特征, 以研究MSDE特征的迁移能力, 如图 2a)所示。可以发现从不同设备上收集到的同类故障信号中提取的MSDE特征的空间角度表现出高度一致性, 如图 2b)中所示。用ϕAic和ϕBjc分别表示A, B 2个数据集中第i个和第j个c类型故障的样本, 这种一致性可以表达如下
|
| 注:N、MT、CT分别代表正常、缺齿和裂齿3种情况;45H表示在45 Hz旋转频率和高负载下收集的数据条件 图 2 MSDE特征的迁移能力示意图 |
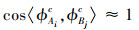
|
(4) |
给定源域和目标域的MSDE特征{xi}i=1n+m, N与M为源域和目标域的样本数。设非线性映射函数z=vTϕ(x), ϕ(x): Rd→H并存在系数矩阵α=[α1, α2, …, αn+m]T, 使得vT=[ϕ(x1), …, ϕ(xn+m)]α, MTSDE的目标函数如下
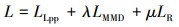
|
(5) |
式中:λ>0是MMD项的折衷参数;μ>0是正则化参数。
1.2.1 LLpp项LLpp项的构建方法与核LPP[4]方法相同, 如公式(6)所示

|
(6) |
式中,K代表核矩阵,Kij=K(xi, xj)=〈ϕ(xi), ϕ(xj)〉=ϕ(xi)Tϕ(xj), D是一个对角矩阵,Dii=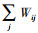
值得一提的是, 在MTSDE方法中, 同一类型的故障的特征作为高维向量, 在空间内具有相似的角度。因此样本邻边的权重与余弦距离而非欧式距离相关, 这能够更好地定义相邻关系。
权重矩阵W的计算如公式(7)所示, 余弦距离的定义如公式(8)所示

|
(7) |
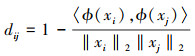
|
(8) |
LLpp项的目的是学习样本之间的角邻接关系, 通过加入LLpp项, 可以使得投影后的样本仍旧保持原有的角邻关系, 这有助于对无标签的目标域样本进行分类。
1.2.2 LMMD项MTSDE的第二个目标是最小化学习过程中2个域的分布差异,直接借鉴最大均值差异(MMD)来描述域间差异。令{C1, C2, …, Cg}∈{1, …, C}代表源域和目标域中共享同类标签的样本, LMMD项计算如公式(9)所示
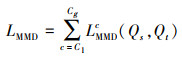
|
(9) |

|
(10) |
式中:Dsc指源域中带有标签c的样本;Dtc指目标域中带有标签c的样本(在本文中, 目标域中只有c=1时的样本可以用来训练模型)。
随后, 将z=vTϕ(x), vT=[ϕ(x1), …, ϕ(xn+m)]α代入公式(10), LMMD可进一步改写为(11)所示的形式
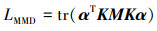
|
(11) |
式中,
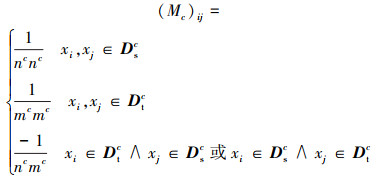
|
(12) |
增加正则化项来控制α的复杂度, 同时, 该正则化项也避免了在求解最小化问题时的秩缺陷, 计算如下
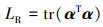
|
(13) |
将(6)、(11)和(13)代入公式(5), 最后模型的目标函数如下
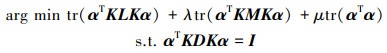
|
(14) |
使用拉格朗日乘子法处理公式(14), 即转化为求解公式(15)。

|
(15) |
上述问题解法类似TCA方法, 最终的解α*是(KLK+λKMK+μI)-1KDK最大的l个特征值对应的特征向量组成的矩阵。
对于测试样本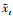
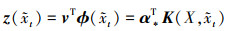
|
(16) |
在迁移模型中有5个参数。每个参数对模型的影响为:σ∈R是热核的尺度参数, 仅影响相似性矩阵的值;k∈N是最近邻节点个数, 控制着邻接图的结构;MMD项折衷参数λ>0与不同域之间的分布差异有关;正则化参数μ>0控制模型的复杂性;子空间的维度参数l∈N影响MTSDE特征的维数。
请注意, 在选择这些参数时需要考虑两点。第一,最优参数是在目标域数据上迭代得到的。在迁移学习情景中, 源域和目标域的数据分布不同, 因此, 传统分类算法的交叉验证策略无法使用。使用MTSDE算法时, 使用源域数据训练模型, 然后使用目标域数据测试不同参数组合下的诊断准确率。最后根据准确率不断更新参数组合, 直到达到最高精度。它可以降低模型的过拟合风险, 提高模型的泛化能力。第二, 需要更高效的搜索算法选择不同的参数组合。在MTSDE算法中, 使用贝叶斯优化算法来对参数组合进行寻优, 而不是传统的网格搜索或随机搜索算法。采取这一策略主要有3个原因:
1) 贝叶斯优化算法利用高斯过程不断更新先验参数信息, 而其他搜索方法不能考虑以前的参数信息。
2) 贝叶斯优化在寻找最佳参数组合时迭代次数更少, 计算效率更高。相比之下, 网格搜索要遍历所有参数组合, 效率低下。
3) 贝叶斯优化在非凸优化问题上性能优于网格搜索方法, 网格搜索方法很容易陷入局部最优解。
1.3 多尺度迁移符号动力学熵(MTSDE)算法流程基于MTSDE算法和SVM分类器的优势, 本文提出的跨域故障诊断策略的实施步骤如下:
1) 提取目标域及源域采样信号的符号动力学熵特征, 将时延参数t选择为1, 嵌入维数m选择范围[2, 5], 类别参数c选择范围[2, 10], 尺度参数τ选择范围为[1, 25];
2) 使用全部源域样本和目标域的正常类型样本训练迁移学习模型, 得到降维投影矩阵α=[α1, α2, , …, αn+m]T∈R(n+m)×l;
3) 根据贝叶斯优化算法, 优化模型的7个超参数:最近邻节点数量k∈[1, 11]、MMD项权重λ∈[0.001, 1 000]、正则化参数、子空间的维数l∈[1, 10], 以及MSDE特征提取时的尺度τ∈[1, 25], 嵌入维数m∈[2, 5], 符号数ε∈[2, 10]。将贝叶斯优化器的参数设置为: 网格尺度20 000, 迭代次数100, 得到最佳的参数组合, 根据最高识别准确率, 生成最终的投影矩阵;
4) 根据公式(16)将变换后的源域及目标域的MTSDE特征输入SVM分类器进行训练, 并计算准确率。
图 3展示了本文方法的计算流程。
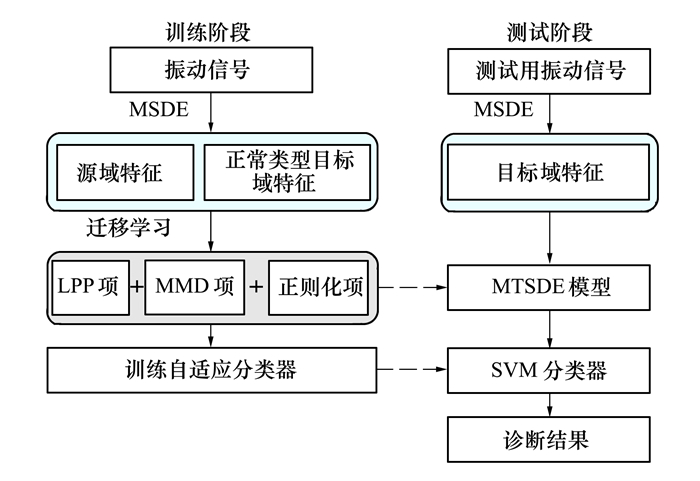
|
| 图 3 MTSDE-SVM跨域智能故障诊断算法的流程 |
1) 齿轮箱数据集
齿轮箱数据集来自预测和健康管理协会2009年数据挑战赛(PHM2009)[18]。图 4展示了实验平台和示意图。实验台由电机、测转矩传感器、测力计和电子控制器组成。加速度计传感器安装在齿轮箱的输入和输出端收集振动数据。这一数据集包含3种健康状态, 包括正常(N)、缺齿(MT)和齿缺陷(CT)。要模拟迁移学习场景, 需要在不同的转速条件下(30, 35, 40, 45和50 Hz)和不同的负载条件下(高负载和低负载)选择数据, 来构建不同分布的数据。模拟不平衡的数据集条件, 每个域包含200个正常样本和100×2个故障样本。在下文中, 数字表示旋转速度, 包括30, 35, 40, 45和50 Hz, “H, L”分别表示“高负载”和“低负载”。例如, 30 H表示在30 Hz旋转速度和高负载条件下采集的样品。
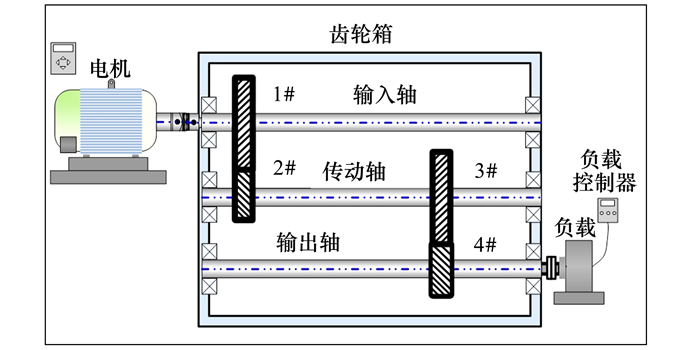
|
| 图 4 齿轮箱试验台的结构示意图 |
2) 滚动轴承数据集
CWRU数据集: 实验二中域A和域B的数据收集自凯斯西储大学的轴承数据中心[19], 因此实验轴承均为SKF 6205-2RS深沟球轴承, 但A和B的操作条件不同。图 5展示了试验台及其结构示意图。数据集A由从电机驱动端以0 kW(1 797 r/min)的速度采集的振动信号组成, 这些振动信号包含4个不同的健康状态: 正常状态(N)、外圈故障(OR)、内圈故障(IR)和球故障(B)。对于OR、IR和B状态, 包括3个严重程度(0.18, 0.36和0.53 mm)的振动信号。数据集B在2.24 kW(1 730 r/min)的条件下采集4种不同的健康状况下的信号, 同样的, 每个故障类别也包含3个严重程度信号。数据集A和B中信号的采样频率为12 kHz, 采样长度为4 000。
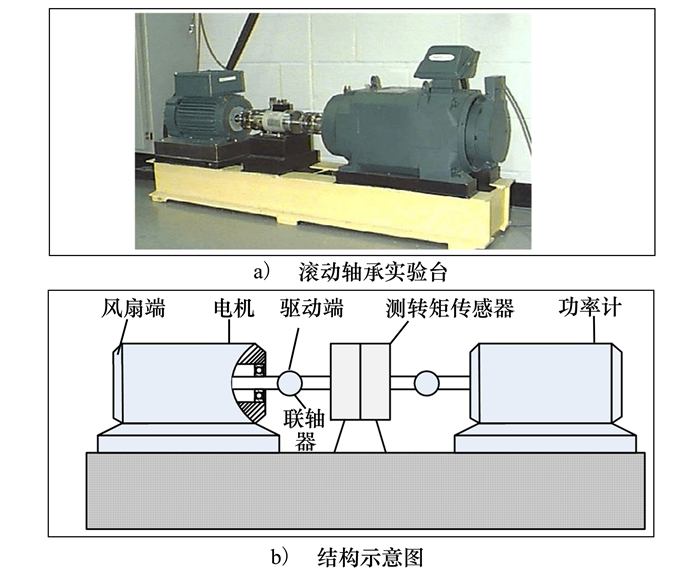
|
| 图 5 试验台及其结构 |
MFPT数据集: 实验二的域C收集自机械故障预防技术学会[20], 实验对象也是深沟球轴承, 但与域A、B使用的型号不同。轴承参数如下: 螺距直径为31.62 mm, 球的直径是5.97 mn, 接触角为0°, 8个球。数据集C包括3种不同健康状态下采集的振动信号: 正常状态、外圈故障和内圈故障, 图 6展示了故障轴承的形态。正常数据选自1 200 N负载下采集的3个信号。外圈故障选择自1 333 N负载。内圈故障选择自1 111 N和1 333 N负载下的信号。轴的转速为1 500 r/min, 从原始信号中每一类采样100个样本, 长度为18 000, 信号的采样率为48 828 Hz。

|
| 图 6 故障轴承的照片 |
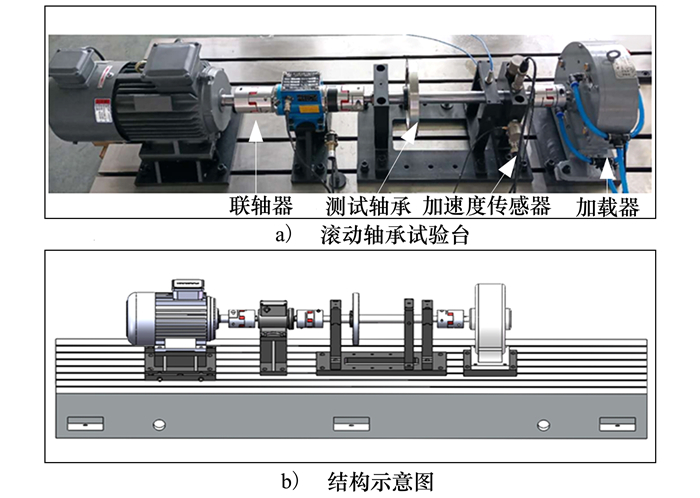
NWPU数据集: 这一数据集在HD-FD-H-03X转子滚动轴承与齿轮箱综合故障实验台上收集得到。实验对象为6205深沟球滚动轴承。实验台的结构如图 7所示。
|
| 图 7 HD-FD-H-03X实验台及其结构示意图 |
本文中使用了通道1的传感器输出的加速度信号。样本在不同的转速(600和1 000 r/min)和负载下(高: H, 中: M, 低: L)收集得到, 并且包含5种健康类型: 正常、内圈点蚀、外圈点蚀、内圈裂纹、外圈裂纹。每一种故障形式又包含3种不同程度的故障(内圈点蚀和外圈点蚀包含1, 2和3 mm; 内圈裂纹和外圈裂纹包含0.2, 0.4和1 mm)。从原始信号中, 每一类故障采样90个样本, 长度为4 000。
2.2 实验设置实验一 变速箱的跨域故障诊断实验。基于PHM09齿轮箱数据集, 在不同的旋转速度和负载下设计了3个故障诊断任务(45H→40L、40L→50H、50L→30H)。同时, 在不同旋转速度, 相同负载条件下设计了3个任务(30H→40H, 40L→50L, 45H→35H), 最后3个任务在不同的负载, 相同转速条件下进行(35L→35H, 40L→40H, 30H→30L)。请注意, 在目标域中, 有一半的正常状态的样本与源域一起训练模型。
实验二 轴承的跨域故障诊断。基于CWRU和MFPT数据集, 设计6个诊断任务。包括4个四类诊断任务(A→B, A→C, B→A, B→C)和2个三类诊断任务(C→A, C→B)。三类诊断任务中, 由于域C没有球故障数据, 删除来自域A和B的球故障样本。
实验三 轴承的跨域故障诊断。基于NWPU数据集, 在不同的转速和负载条件下设计6个诊断任务(600M→1 000H, 600L→1 000H, 600H→1 000M, 1 000H→600L, 1 000L→600H, 1 000M→600H)。
2.3 对照方法为了展示本文提出的智能故障诊断方法的优越性, 将3个传统分类算法和3个迁移学习方法设置为对照组。
实施以下7种方法时, 首先提取训练集和测试集的MSDE特征作为输入。
1) MSDE-SVM
直接使用训练集的MSDE特征训练SVM分类器, 称为MSDE-SVM方法。然后, 测试集的分类准确率为输出。实现SVM使用了LIBSVM工具箱。并应用RBF核函数, 将权衡参数c的设置为1。
2) MSDE-KNN
实验流程与MSDE-SVM相同, 但使用k近邻(KNN)分类器代替SVM。在范围{1, 5, 9, 13, 17, 21, 25, 29, 33, 63}中搜索最近邻节点的个数, 然后取准确率最高的情况作为输出。
3) MSDE-LR
实验流程与方法1)和方法2)类似, 但采用逻辑回归(LR)分类方法, 并在范围{0.001, 0.01, 0.1, 1, 10}中搜索最佳权衡参数。输出最高的准确率。
4) MSDE-GFK-SVM
这是一种迁移学习算法, 对于MSDE-GFK算法, 首先提取MSDE特征, 然后通过测地层流式核(GFK)方法将源域特征映射到目标域空间[21], 最后使用SVM分类器对映射后的特征进行分类。这里采用的子空间嵌入方法是主成分分析(PCA)。
5) MSDE-SSTCA-SVM
将MSDE特征输入半监督迁移成分分析(SSTCA)模型[15]。最优超参数由贝叶斯优化方法搜索。分别在范围[1, 25](在实验一中是[1, 50]), [10-3, 103], [1, 10], [10-3, 1]和[10-3, 103]搜索MSDE尺度因子τ、正则化权衡参数μ1、子空间维度l1、监督项权衡参数γ1和几何项权衡参数λ1。最后将低维特征输入SVM分类器并输出诊断精度。
6) MSDE-DAFD-SVM
该方法是基于神经网络的迁移学习算法, 将域深度神经网络(DAFD)作为迁移策略[22]。MSDE特征被输入一个3层的神经网络, 然后使用SVM分类器对输出特征进行分类。
7) MTSDE-SVM
MTSDE-SVM智能故障诊断模型的具体计算流程参照本文第1.3节。对于此方法, 将热核参数设置为常数1。然后应用贝叶斯优化算法在超参数空间中搜索MTSDE-SVM方法的最佳参数。分别在范围[1, 25](在实验一中是[1, 50]), [1, 10], [1, 10], [10-3, 103]和[10-3, 103]内搜索参数τ, k, l, λ和μ。此外, SVM中出现的2个参数c和g也使用贝叶斯方法进行了优化。在范围(0, 8]中搜索他们, 并得到最终的准确率。
注意, 所有实验中, 识别准确率采用公式(17)计算
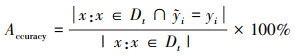
|
(17) |
1) 诊断准确率分析
实验一 变速箱的跨域故障诊断实验准确率如表 1所示。结果表明, 本文提出的方法在7种方法中识别精度最高, 这证实了MTSDE能够提取出具有迁移性的特征。3种传统方法: MSDE-SVM、MSDE-KNN和MSDE-LR由于缺乏知识迁移过程, 分类精度较低。迁移学习方法中, MSDE-SSTCA-SVM的性能略好于上述3种传统方法, 跨域分类准确度较高。MSDE-GFK方法在30H~40H、45H~35H等单个诊断任务中展现了较好的结果, 但随着源域和目标域的变化, 结果并不稳定。与这些方法相比, 基于神经网络的MSDE-DAFD算法执行效果不佳。
| Case Ⅰ | MTSDE-SVM | MSDE-SVM | MSDE-KNN | MSDE-LR | MSDE-SSTCA-SVM | MSDE-GFK-SVM | MSDE-DAFD-SVM |
| 45H→40L | 100.0 | 66.7 | 67.0 | 67.0 | 66.7 | 66.7 | 35.0 |
| 40L→50H | 100.0 | 66.7 | 95.3 | 71.3 | 87.3 | 66.7 | 35.7 |
| 50L→30H | 83.3 | 60.7 | 66.7 | 99.3 | 66.7 | 66.3 | 35.0 |
| 30H→40H | 100.0 | 68.0 | 100.0 | 100.0 | 100.0 | 90.3 | 36.7 |
| 40L→50L | 99.0 | 66.7 | 66.7 | 66.7 | 71.0 | 66.7 | 35.0 |
| 45H→35H | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 35.0 |
| 35L→35H | 100.0 | 66.7 | 66.7 | 66.7 | 66.7 | 66.7 | 35.0 |
| 40L→40H | 99.3 | 66.7 | 80.7 | 66.7 | 67.0 | 66.7 | 35.0 |
| 30H→30L | 100.0 | 46.0 | 66.7 | 92.7 | 100.0 | 66.7 | 33.3 |
| 平均 | 97.9 | 67.6 | 78.9 | 81.2 | 80.6 | 73.0 | 35.1 |
最后, 本文方法的准确率高达97.9%。对照实验结果表明, 本文方法不仅能有效地将诊断知识从源域转移到目标域, 而且能在相关性假设下保持跨域故障数据的分布结构信息。
实验二 实验二的分类结果在表 2中。实验结果表明, 本文提出的方法平均准确度为97.1%, 是7种方法中最高的。MTSDE算法优势的一个重要解释是, 本文方法使用余弦距离来定义相似性, 从而在投影后更好地保存了数据的分布特性。7种方法的诊断能力排名与实验一的结果相似, 这进一步验证了MTSDE在迁移故障诊断中的优势。例如, 2个实验A→C和B→C的准确率达到100%, 而MSDE-SSTCA-SVM方法在这2个实验中性能不佳。
| Case Ⅱ | MTSDE-SVM | MSDE-SVM | MSDE-KNN | MSDE-LR | MSDE-SSTCA-SVM | MSDE-GFK-SVM | MSDE-DAFD-SVM |
| A→B | 100.0 | 99.2 | 92.5 | 95.8 | 98.3 | 92.5 | 47.3 |
| B→A | 98.9 | 94.2 | 97.5 | 82.2 | 96.9 | 81.1 | 46.3 |
| A→C | 100.0 | 66.7 | 89.3 | 33.3 | 66.7 | 33.3 | 39.4 |
| C→A | 89.3 | 77.4 | 77.4 | 69.6 | 77.4 | 88.9 | 36.4 |
| B→C | 100.0 | 66.7 | 100.0 | 33.3 | 66.7 | 33.3 | 42.5 |
| C→B | 94.1 | 77.8 | 75.6 | 66.7 | 77.4 | 92.20 | 35.3 |
| 平均 | 97.1 | 80.3 | 88.7 | 63.5 | 80.6 | 70.2 | 41.2 |
实验三 实验三的分类结果呈现在表 3中。MTSDE-SVM方法的诊断准确率略低于实验一和实验二, 但仍然达到了90.3%, 超过了其他6种方法。值得一提的是, 直接将MSDE特征输入SVM分类器的MSDE-SVM方法取得了85.7%的诊断准确率, 这直接体现了选用的MSDE特征提取算法的优越性。
| Case Ⅲ | MTSDE-SVM | MSDE-SVM | MSDE-KNN | MSDE-LR | MSDE-SSTCA-SVM | MSDE-GFK-SVM | MSDE-DAFD-SVM |
| 600M-1 000H | 92.9 | 86.0 | 66.7 | 80.7 | 72.2 | 84.9 | 22.9 |
| 600L-1 000H | 90.9 | 84.9 | 65.6 | 66.4 | 70.9 | 84.4 | 21.8 |
| 600H-1 000M | 82.0 | 77.6 | 59.6 | 69.6 | 72.9 | 81.1 | 22.9 |
| 1 000H-600L | 92.4 | 90.2 | 58.2 | 64.0 | 80.9 | 88.4 | 22.2 |
| 1 000L-600H | 90.2 | 88.0 | 56.9 | 70.4 | 79.1 | 88.4 | 22.1 |
| 1 000M-600H | 93.1 | 87.6 | 54.9 | 72.7 | 85.8 | 87.1 | 22.7 |
| 平均 | 90.3 | 85.7 | 60.3 | 70.6 | 77.0 | 85.7 | 22.4 |
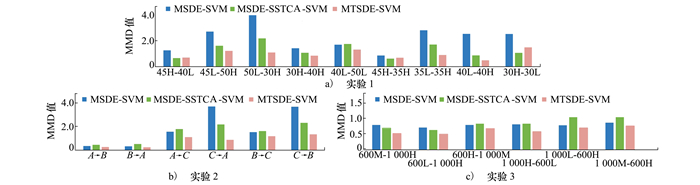
2) 分布差异分析
为了进一步验证MTSDE的有效性, 用MMD统计量衡量了不同方法处理前后源域和目标域之间共享类样本的联合分布距离[23-24]。计算了MSDE-SVM、MSDE-SSTCA-SVM方法和MTSDE-SVM方法的MMD值并进行比较。为了公平, 特征参数提取时的参数均设置为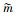
图 8展示了获得的结果。可以观察到, 使用本文提出的方法处理后, MMD值显著降低, 这意味着源域和目标域之间的分布差异大大降低, 从而在不同的工况下为数据提供更好的迁移能力。
|
| 图 8 MMD值直方图 |
3) 故障特征可视化分析
为了直观地说明本文方法的有效性, t-SNE方法用于直观地处理原始MSDE空间、SSTCA空间和MTSDE空间中的数据[25]。每个实验中任选一个任务展示其二维可视化结果。原始MSDE特征的参数设置为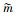
实验一的数据来自不同的负载条件,其中二维投影结果显示在图 9中。可以明显看出,SSTCA方法显著地将不同的样本聚类在一起。然而,一些正常的样本与缺齿故障样本完全吻合。因此,MTSDE性能更好,分类精度更高。图 10展示从不同数据集收集的实验二的源域和目标域数据的投影结果。在相同类型的不同机械的诊断情景中,MTSDE方法仍可以聚类相同的故障样本,具有更好的诊断性能。

|
| 图 9 特征可视化 |

|
| 图 10 特征可视化 |
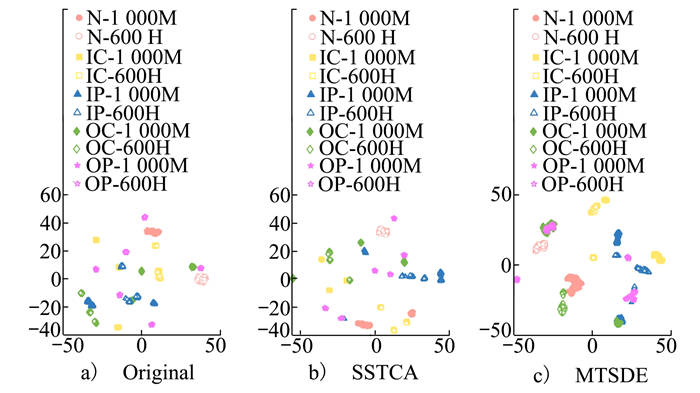
实验三的数据是从不同转速和负载下的机器中收集的。图 11展示了特征在MTSDE、SSTCA和原始空间中的二维可视化图像。在3种方法中,本文方法具有最佳的聚类性能。图 11c)中显示,在MTSDE空间中,同类型故障样本聚类形成的簇更少,使用源域数据(以及目标域的正常数据)在MTSDE空间中训练出的分类模型更有可能正确识别目标域的样本。该现象验证了该方法可以将故障诊断问题知识从源域迁移到目标域。
|
| 图 11 特征可视化(1 000M-600 H) |
本文提出了基于MTSDE-SVM智能故障诊断方法,用于旋转机械故障诊断。首先,从训练样本中提取MSDE特征。其次,通过迁移学习模型将特征降维得到MTSDE特征,在这个过程中,训练集和测试集的数据分布差异显著减小。最后,MTSDE特征作为输入,训练SVM分类器用于辨别故障类型。本文的主要贡献包括:
1) 在多尺度符号动力学熵的基础上,结合特征迁移学习思想提出一种新的特征提取方法-多尺度迁移符号动力学熵。通过提取具有迁移能力的特征,可以使用非同分布的数据训练诊断模型,从而解决实际生产中标记数据不足的问题。
2) 在参数优化过程中还对MSDE特征的尺度参数、符号数和嵌入维度进行了寻优,这有助于提高诊断精度。
3) 对滚动轴承的故障诊断实验表明,与其他传统机器学习方法相比,本文方法可以获得更高的诊断精度。这意味着本文提出的方法具有良好的实际应用前景,为不同工况下轴承故障诊断提供了一种新思路。
| [1] | LIU H, LIU C, HUANG Y. Adaptive feature extraction using sparse coding for machinery fault diagnosis[J]. Mechanical Systems and Signal Processing, 2011, 25: 558-574. DOI:10.1016/j.ymssp.2010.07.019 |
| [2] | LI Y, WANG X, LIU Z, et al. The entropy algorithm and its variants in the fault diagnosis of rotating machinery: a review[J]. IEEE Access, 2018, 6: 66723-66741. DOI:10.1109/ACCESS.2018.2873782 |
| [3] | LI Y, LIU F, WANG S. Multi-scale symbolic lempel-ziv: an effective feature extraction approach for fault diagnosis of railway vehicle systems[J]. IEEE Trans on Industrial Informatics, 2021, 17: 199-208. DOI:10.1109/TII.2020.2980923 |
| [4] | YANG C, JIA M. Hierarchical multiscale permutation entropy-based feature extraction and fuzzy support tensor machine with pinball loss for bearing fault identification[J]. Mechanical Systems and Signal Processing, 2021, 149: 107182. DOI:10.1016/j.ymssp.2020.107182 |
| [5] | WEI Y, LI Y, XU M, et al. A review of early fault diagnosis approaches and their applications in rotating machinery[J]. Entropy, 2019, 21(4): 409. DOI:10.3390/e21040409 |
| [6] | KOLMOGOROV A N. A new metric invariant of transient dynamical systems and automorphisms in Lebesgue spaces[J]. Doklady Akademii nauk SSSR, 1958, 119: 861-864. |
| [7] | PINCUS S. Approximate entropy(ApEn) as a complexity measure[J]. Chaos, 1995, 5(1): 110-117. DOI:10.1063/1.166092 |
| [8] | RICHMAN J, MOORMAN J. Physiological time-series analysis using approximate entropy and sample entropy[J]. American Journal of Physiology-Heart and Circulatory Physiology, 2000, 278: H2039-49. DOI:10.1152/ajpheart.2000.278.6.H2039 |
| [9] | CHEN W, ZHUANG J, YU W, et al. Measuring complexity using FuzzyEn, ApEn, and SampEn[J]. Medical Engineering & Physics, 2009, 31(1): 61-68. |
| [10] | CHRISTOPH B. Permutation entropy: a natural complexity measure for time series[J]. Physical Review Letters, 2002, 17(88): 174102. |
| [11] | LI Y, YANG Y, LI G, et al. A fault diagnosis scheme for planetary gearboxes using modified multi-scale symbolic dynamic entropy and mRMR feature selection[J]. Mechanical Systems and Signal Processing, 2017, 91: 295-312. DOI:10.1016/j.ymssp.2016.12.040 |
| [12] | COSTA M, GOLDBERGER A L, PENG C K. Multiscale entropy analysis of complex physiologic time series[J]. Physical Review Letters, 2007, 89: 068102. |
| [13] | PAN S J, KWOK J T, YANG Q. Transfer learning via dimensionality reduction[C]//Proceedings of the 23rd National Conference on Artificial Intelligence, Chicago, Illinois, 2008 |
| [14] | QUANZ B, HUAN J. Large margin transductive transfer learning[C]//Proceedings of the 18th ACM Conference on Information and Knowledge Management, Hong Kong, China, 2009 |
| [15] | PAN S J, TSANG I W, KWOK J T, et al. Domain adaptation via transfer component analysis[J]. IEEE Trans on Neural Networks, 2011, 22(2): 199-210. DOI:10.1109/TNN.2010.2091281 |
| [16] | ZHENG H, WANG R, YIN J, et al. A new intelligent fault identification method based on transfer locality preserving projection for actual diagnosis scenario of rotating machinery[J]. Mechanical Systems and Signal Processing, 2020, 135: 106344. DOI:10.1016/j.ymssp.2019.106344 |
| [17] | Pan S J, Yang Q. A survey on transfer learning[J]. IEEE Trans on Knowledge and Data Engineering, 2010, 22(10): 1345-1359. DOI:10.1109/TKDE.2009.191 |
| [18] | PHM Society. PHM 09 Data Challenge Data[EB/OL]. (2009-04-10)[2021-09-25]. https://www.phmsociety.org/data-analysis-competition/ |
| [19] | CASE Western Reserve University. Case western reserve university rolling bearing dataset[EB/OL]. (2021-08-05)[2021-09-25]. https://csegroups.case.edu/bearingdatacenter/pages/12k-drive-end-bearing-fault-data |
| [20] | Society for Machinery Failure Prevention Technology. Eric Bechhoefer, MFPT bearing fault data sets[EB/OL]. (2021-02-27)[2021-09-25]. https://mfpt.org/fault-data-sets/ |
| [21] | GONG B, SHI Y, SHA F, et al. Geodesic flow kernel for unsupervised domain adaptation[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition, 2012 |
| [22] | LU W, LIANG B, CHENG Y, et al. Deep model based domain adaptation for fault diagnosis[J]. IEEE Trans on Industrial Electronics, 2016, 64(3): 2296-2305. |
| [23] | ZHAO J, MENG D. Fastmmd: ensemble of circular discrepancy for efficient two-sample test[J]. Neural Computation, 2015, 27(6): 1345-1372. DOI:10.1162/NECO_a_00732 |
| [24] | LONG M, WANG J, DING G, et al. Adaptation regularization: a general framework for transfer learning[J]. IEEE Trans on Knowledge and Data Engineering, 2013, 26(5): 1076-1089. |
| [25] | VAN DER MAATEN L, HINTON G. Visualizing data using t-SNE[J]. Journal of Machine Learning Research, 2008, 9: 2579-2609. |




