2. 西北工业大学 空天微纳系统教育部重点实验室, 陕西 西安 710072
MEMS微镜[1]是指在硅晶圆上通过半导体工艺制造的光束操纵芯片,其可以通过静电、电热、电磁、压电等[2-5]多种驱动方式,实现芯片内反射镜面的偏转以对反射光束的方向进行调制,在激光雷达、三维相机和激光投影[6-8]领域广泛使用。静电驱动的MEMS微镜因为其制造工艺与半导体兼容性好、响应速度快、功耗低,是常用的MEMS微镜。但是相比电磁、电热和压电驱动的MEMS微镜,静电MEMS微镜在矢量扭转或者准静态扭转[9]模式下的扫描角度较小,一般需要工作在谐振扭转模式下以获得激光测量或者激光显示需要的大扫描视场角。静电MEMS微镜扭转角度的实时和准确检测,对于闭环控制非常重要,并直接影响到应用系统的精度和性能。对于静电MEMS振镜,电容法和光电法是常用的扭转角检测方法。其中光电法是用光电传感器直接测量由MEMS微镜反射的光束的光斑位置,不易受到温漂的影响,适用于角度精度要求较高的场景中。为了降低光电法扭转角测量的成本,MEMS微镜产品中的光电法实时扭转角度检测并不会像实验室中那样,使用昂贵的位置敏感检测器(position sensitive detector, PSD)去连续监测反射光斑的位置[10],而是先假设扭转轨迹是正弦曲线[11],然后通过在扫描光路中设置2个高速光敏二极管,根据2个光敏二极管的位置关系及扫描光束经过2个光敏二极管的时间,获得MEMS微镜的扭转相位和振幅,并按照正弦曲线的角度/时间轨迹去估计任意时刻MEMS微镜的扭转角。
但是,在实际MEMS微镜的驱动电路中,由于方波的功率密度大且造波电路简单,MEMS微镜普遍都是用方波[12]而非正弦波进行驱动。方波相比正弦波,含有高次谐波成分,其对MEMS微镜进行驱动时,可能会激发出MEMS微振镜的高阶扭转模态响应,并和低阶扭转模态响应叠加,导致扭转角度/时间关系曲线偏离理想的正弦曲线。这种偏差的存在,会引起非常微小的角度计算误差,但是这种非常微小的角度计算误差会造成三维相机标定参数的变化,导致激光雷达扫描方向的失配和激光显示像素位置的偏移,极大地影响应用光学系统的测量精度和定位精度。
方波驱动下MEMS微振镜扭转角度/时间曲线偏离标准正弦曲线的程度目前尚不清楚。本文通过显微激光多普勒方法,对MEMS微镜谐振扭转轨迹进行实际测量,对比实际测量的扭转轨迹偏离正弦轨迹的程度,并明确偏离正弦轨迹的原因,为MEMS微镜的扭转角度估计提供误差参考和指导。
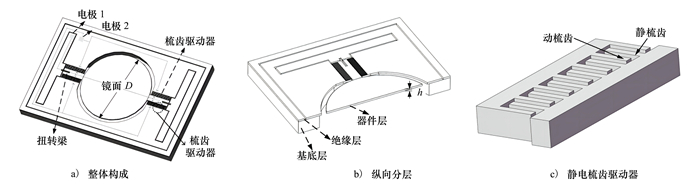
1 实验设计与实施 1.1 MEMS微镜及其静电谐振驱动方法测试使用的MEMS微镜为知微传感技术有限公司的C1100型微镜,其结构示意图如图 1a)所示。微镜由直径为D的镜面、梳齿驱动器和扭转梁构成。整个微镜由一片SOI晶圆制成,其纵向分层如图 1b)所示,其中梳齿驱动器、镜面和扭转梁位于SOI晶圆的器件层, 梳齿高度和镜面厚度由器件层厚度h决定,器件层和作为机械支撑的基底层之间由二氧化硅绝缘层隔开。梳齿驱动器结构如图 1c)所示,由动梳齿和静梳齿构成,其中,静梳齿固定在整个框架上并连接到电极2上,而动梳齿则与镜面和扭转梁相连,并统一连接到电极1上。
|
| 图 1 MEMS微镜结构示意图 |
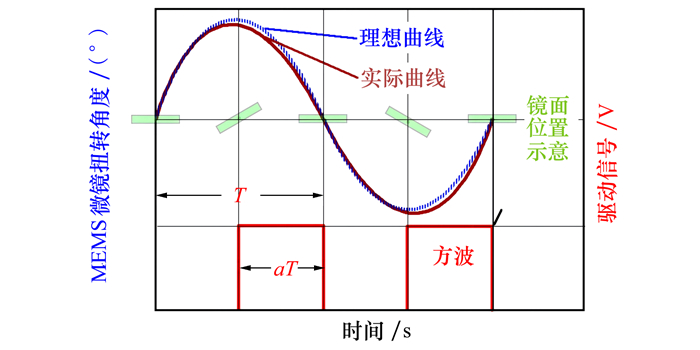
在电极1和电极2之间施加如图 2所示的周期为T,占空比为a的方波,MEMS微镜的梳齿驱动器在方波驱动下产生交变的静电力,驱动镜面围绕扭转梁以周期2T往复扭转振动,一般认为理想状态下其扭转角度与时间的关系符合扭转频率是驱动方波频率1/2的正弦曲线,但是实际上由于方波中存在高次谐波干扰,实际的扭转角度曲线存在一定的偏离,而这种偏离的具体程度就是本论文要研究的内容。
|
| 图 2 MEMS微镜静电驱动方波和对应的扭转角轨迹示意图 |
静电驱动的MEMS微镜因为静电力与扭转角度的关系存在非常强的非线性,所以其扭转幅频特性曲线并不呈现沿着谐振频率点左右对称的形状,而是向高频或者低频偏斜。本研究中使用的C1100微镜的扭转谐振频率曲线如图 3所示,存在f1, f2, f3 3个特征频率点。当从低频向高频正向扫描时,微镜在频率f2处起振,其振幅随着频率的升高而降低,一直到频率f3处停振。当从高频向低频反向扫描时,微镜在频率f3处起振,其振幅随着频率的降低而升高,一直到频率f1处停振。

|
| 图 3 MEMS微镜扭转谐振幅频特性曲线示意图 |
3个特征频率的值并不固定,而是随驱动方波幅值和占空比的变化而变化。本研究所使用的C1100镜面直径为1.3 mm,镜面厚度为50 μm,当驱动方波占空比为50%时,其在不同驱动电压下的3个特征频率如表 1所示。为了保证微镜在不同驱动电压下能够顺利起振,并考虑到驱动方波的频率应该是扭转频率的2倍,本研究将驱动方波频率的选取范围设定为11 150~11 280 Hz。共选取5个频率值进行扭转轨迹测量,分别为11 150, 11 182, 11 215, 11 247, 11 280 Hz。特别需要注意的是,当驱动方波频率介于2倍的f1和f2之间时,应该先在大于2倍的f2频率下使MEMS微镜起振,然后降低频率到想要的目标频率,否则MEMS微镜将无法直接起振。
| 驱动电压/V | f1 | f2 | f3 |
| 60 | 5 572 | 5 588 | 5 653 |
| 70 | 5 573 | 5 593 | 5 681 |
| 80 | 5 573 | 5 601 | 5 716 |
本研究利用舜宇公司的LV-S01-M型显微激光多普勒设备来非接触测量MEMS振镜扭转角度和时间的关系,其采用VD-16高精度数字位移解码器,位移分辨率优于15 pm。测试系统的原理图如图 4所示。

|
| 图 4 MEMS微镜扭转角度的显微激光多普勒测量方案 |
电脑控制驱动信号发生器产生频率和幅值可调节的方波驱动MEMS微镜谐振扭转,显微激光多普勒将微米级的光斑投射到MEMS微镜上离旋转轴心距离为d的点,进行面外垂直方向上的速度v(t)和位移y(t)的测量。
将采集的离散数据通过三角函数变换和曲线拟合,最终得到机械扭转角θM和时间t的函数关系。机械扭转角θM(t)和面外位移y(t)的关系如(1)式所示。

|
(1) |
距离d可以在显微激光多普勒测试系统的图像测试软件界面进行测量。距离d的选取对于测量的精度有一定的影响。当距离d取值较大时,测量的面外位移y比较显著,但是会导致微镜镜面上的显微激光多普勒的光斑大小在测量过程中随纵向移动而产生较大波动,进而引入测量误差;当距离d取值较小时,面外位移y过小而无法准确测量。经过多次测量对比,本研究选取了离扭转轴心距离d为100 μm的点进行显微激光多普勒测量。
考虑到MEMS微镜在激光雷达和三维相机中应用时,其作用是对入射到微镜上的光束方向进行偏转调制,关注的是从MEMS微镜上反射回来的光束扫描角度变化。而被MEMS微镜反射的光束扫描光学角θO和微镜机械扭转角θM的关系是:
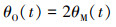
|
(2) |
分别在如1.1节所给出的3个驱动电压下和5个驱动方波频率下进行驱动,共进行了15组显微激光多普勒振动实验来获取C1100型MEMS微镜在不同驱动电压和驱动频率下的扭转角度与时间关系。当驱动电压是60 V,驱动频率是11 150 Hz时,利用MATLAB将所测得的机械扭转角进行正弦拟合,得到的拟合结果如(3)式所示。
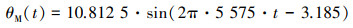
|
(3) |
将正弦拟合得到的扭转角轨迹作为理想轨迹,并绘制出理想轨迹与实测轨迹的偏差图,如图 5所示。
|
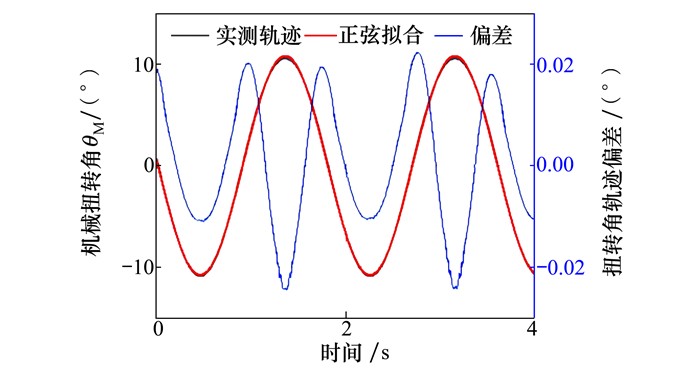
| 图 5 60 V驱动电压和11 150 Hz驱动频率下的扭转角轨迹 |
在其他驱动电压和驱动方波频率下得到的实测轨迹和拟合正弦轨迹偏离的趋势和图 5类似,直接以表 2的形式给出实测轨迹和拟合正弦轨迹的偏差范围。
| 驱动频率/ Hz |
不同驱动电压下的轨迹偏差范围/(°) | ||
| 60 V | 70 V | 80 V | |
| 11 150 | -0.023 9~0.025 6 | -0.024 0~0.044 0 | -0.029 7~0.046 0 |
| 11 182 | -0.006 1~0.005 9 | -0.011 9~0.017 5 | -0.013 6~0.019 6 |
| 11 215 | -0.002 9~0.002 5 | -0.004 3~0.005 9 | -0.006 5~0.007 1 |
| 11 247 | -0.002 3~0.002 4 | -0.003 1~0.003 1 | -0.003 4~0.006 3 |
| 1128 0 | -0.001 5~0.001 6 | -0.002 8~0.002 9 | -0.003 0~0.003 7 |
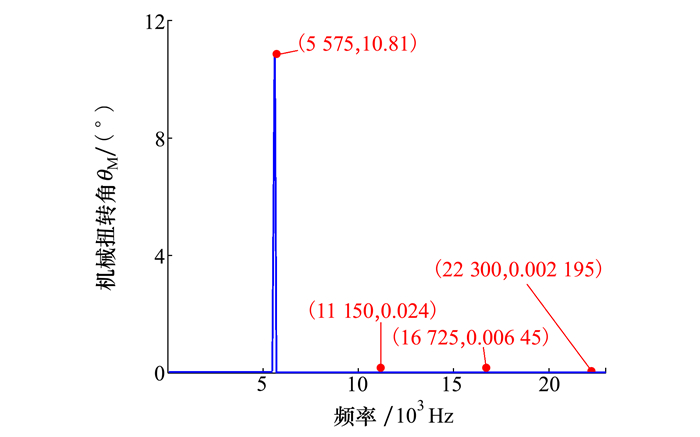
由图 5可知,MEMS微镜的扭转角虽然可以近似为正弦轨迹,但是这种近似是存在一定偏差的,这种偏差并不固定,而是存在一定的波动性,在微镜达到平衡位置和最大转角时,这种偏差相对较大。由表 2又可知,在同样的驱动方波电压下,驱动方波频率越小,也就是MEMS微镜的扭转频率越接近其特征频率f1,其扭转振幅越大,此时其扭转角的拟合正弦轨迹偏离实际扭转轨迹的幅度越大;而在同样的驱动方波频率下,驱动电压越高,MEMS微镜的扭转角振幅越大,此时其扭转角拟合正弦轨迹偏离实际扭转轨迹的幅度也越大。为了探究正弦拟合偏差存在的根源,将测量的时域扭转角数据通过快速傅里叶变换转化到频域,图 6给出了当驱动电压为60 V,驱动频率为11 150 Hz时,实测轨迹的频域信息。从图 6可以看出,实测轨迹除了有频率为驱动方波频率1/2倍的正弦信号以外,还叠加了频率为驱动方波频率1倍、3/2倍和2倍的正弦信号。其中,频率为驱动方波频率1倍叠加信号的幅值比较显著,达到0.024°量级,与图 5中偏差的最大值接近,基本可以判定正弦拟合存在偏差主要是因为实际扭转角轨迹存在多个频率成分,无法用单个频率成分的正弦信号完全描述。
|
| 图 6 60 V驱动电压和11 150 Hz驱动频率下的扭转角轨迹的频域特性 |
总体而言,方波驱动下MEMS微镜的谐振扭转角轨迹使用和扭转频率同频的正弦轨迹来拟合是存在偏差的,而这种偏差是随着谐振扭转振幅的增大而增大的。实验测得的机械扭转角最大偏差可以达到0.046 0°(80V, 11 150 Hz驱动信号下)的数值,而因为被MEMS微镜调制光束的光学角是机械扭转角的2倍,那么光学角的偏差则达到了0.1°的量级。如果集成MEMS微镜的是自动驾驶用激光雷达,那么这已经接近了自动驾驶激光雷达场景中应用时的常用光学角度分辨率0.1°,这种偏差是不能接受的;而如果集成MEMS微镜的是家用扫地机器人的激光雷达,通常光学角度分辨率为1°,那这种偏差带来的影响则并不显著。
3 结论当使用方波驱动静电MEMS微镜时,其扭转角和时间关系并不完全符合标准正弦曲线,存在一定的偏差。这种偏差的最大值随着MEMS微镜振幅的增大而增大,也就是驱动方波的幅值越大,扭转频率越接近MEMS微镜的f1特征频率,这种偏差就越显著。通过频域分析,可以看出这种偏差存在的主要原因是扭转角轨迹并不是单一频率成分的正弦波,而是多个正弦波的叠加信号,除了用于轨迹拟合的频率为驱动方波频率1/2倍的正弦信号比较显著以外,频率为驱动方波频率1倍的正弦信号也比较显著,是导致单频率正弦拟合存在偏差的主要原因。虽然知道了拟合偏差存在的原因,但因为在实际的双光敏二极管测量方法中无法同时准确测量多个频率正弦信号的相位,同时利用多个频率的正弦信号来提高拟合精度是不可行的。正弦拟合方法仅适用于角度精度低于0.1°的扫描角预测场景,而对于角度精度优于0.1°的扫描角预测场景,最好使用PSD器件去连续测量扭转角的实际数值。
| [1] | HOLMSTRÖM S T S, BARAN U, UREY H. MEMS laser scanners: a review[J]. Journal of Microelectromechanical Systems, 2014, 23(2): 259-275. DOI:10.1109/JMEMS.2013.2295470 |
| [2] | BRUNNER D, YOO H W, SCHITTER G. Linear modeling and control of comb-actuated resonant MEMS mirror with nonlinear dynamics[J]. IEEE Trans on Industrial Electronics, 2020, 68(4): 3315-3323. |
| [3] | LIU T, PAN T, WANG P, et al. Scanning optimization of an electrothermally-actuated MEMS mirror for applications in optical coherence tomography endoscopy[J]. Sensors and Actuators A: Physical, 2022, 335: 113377. DOI:10.1016/j.sna.2022.113377 |
| [4] | JIANG B, PENG M, LIU Y, et al. The fabrication of 2D micromirror with large electromagnetic driving forces[J]. Sensors and Actuators A: Physical, 2019, 286: 163-168. DOI:10.1016/j.sna.2018.12.038 |
| [5] | GU-STOPPEL S, LISEC T, FICHTNER S, et al. A highly linear piezoelectric quasi-static MEMS mirror with mechanical tilt angles of larger than 10[C]//MOEMS and Miniaturized Systems XVIII. SPIE, 2019, 10931: 1093102 |
| [6] | SCHWARZ F, SENGER F, ALBERS J, et al. Resonant 1D MEMS mirror with a total optical scan angle of 180° for automotive LiDAR[C]//Conference on MOEMS and Miniaturized Systems, 2020: 46-62 |
| [7] | YANG D, QIAO D, XIA C. Curved light surface model for calibration of a structured light 3D modeling system based on striped patterns[J]. Optics Express, 2020, 28(22): 33240-33253. DOI:10.1364/OE.408444 |
| [8] | SEO Y H, HWANG K, KIM H, et al. Scanning MEMS mirror for high definition and high frame rate Lissajous patterns[J]. Micromachines, 2019, 10(1): 67. DOI:10.3390/mi10010067 |
| [9] | PARK S, WAKELIN M, MALEA D, et al. Low-power, small-form-factor angle sensing circuit for an electrostatic, quasi-static MEMS mirror in AR applications[C]//Optical Architectures for Displays and Sensing in Augmented, Virtual, and Mixed Reality(AR, VR, MR)Ⅲ, SPIE, 2022 |
| [10] | YOO H W, BRUNNER D, THURNER T, et al. MEMS test bench and its uncertainty analysis for evaluation of MEMS mirrors[J]. IFAC-PapersOnLine, 2019, 52(15): 49-54. DOI:10.1016/j.ifacol.2019.11.648 |
| [11] | TORTSCHANOFF A, LENZHOFER M, FRANK A, et al. Position encoding and phase control of resonant MOEMS mirrors[J]. Sensors and Actuators A: Physical, 2010, 162(2): 235-240. DOI:10.1016/j.sna.2010.01.011 |
| [12] | PHAM D D, SINGH R P, YAN D L, et al. Position sensing and electrostatic actuation circuits for 2-D scanning MEMS micromirror[C]//2011 Defense Science Research Conference and Expo, 2011: 1-4 |
2. Ministry of Education Key Lab of Micro/Nano Systems for Aerospace, Northwestern Polytechnical University, Xi'an 710072, China




