2. 西安精密机械研究所, 陕西 西安 710077;
3. 西北工业大学 航空学院, 陕西 西安 710072
随着计算机科学和计算流体力学的快速发展,数值模拟有效弥补了风洞试验的不足,已成为流致噪声研究不可替代的重要手段。数值模拟不仅可以精细化模拟声源,还可以分析噪声传播特性。这有助于对噪声的产生、传播和反射等物理机制进行更加深入的研究。流致噪声产生的物理本质是流动引起的压力脉动,尾缘流致噪声包括复杂的湍流噪声和流体与固边界之间相互作用的噪声。因此,流致噪声的数值计算精度依赖于声源产生与传播的求解精度,需采用低耗散、低色散数值方法进行精细化模拟[1-2]。
在流致噪声数值计算方面,目前主要采用2种数值方法[3]进行模拟分析:直接数值方法和混合数值方法。
直接数值模拟方法的基本思路是将流场与声场统一处理,通过求解可压缩纳维-斯托克斯(Navier-Stokes, NS)方程来模拟声源的产生以及传播过程。虽然该方法在理论上可获得很高的模拟精度,但其仍然存在一些缺陷。例如:声学扰动易淹没在数值误差中,整个计算域均需采用高精度、低耗散低色散数值方法和准确的边界条件。相比于直接数值模拟方法,综合计算资源与工程应用价值等方面的考虑,混合数值方法是一种处理复杂构型声学问题合理有效的技术手段。该方法采用一种分区求解的策略,将整个物理过程划分为2个或3个计算区域[4-5]:声源区域,主要是复杂流动变化引起的流场脉动;声传播区域,主要是描述声源的传播过程,可考虑声波的反射、衍射、折射等现象。
声源区域声源求解通常采用诸如大涡模拟(large eddy simulation, LES)、RANS/LES模拟等[6-7]方法获得,其难点在于湍流的高精度数值模拟。此外,在一些宽频噪声预测问题中,也可通过求解RANS(Reynolds average NS equations)获得湍流平均信息生成噪声源项,类似于SNGR(stochastic noise generation and radiation)、RPM(random particle mesh)、FRPM(fast random particle mesh)等[7-9]湍流统计声源法。湍流声源统计方法主要依赖于湍流自身的统计信息,相比于RANS/LES、LES、DNS等方法,其计算效率更高,目前已在翼型后缘湍流噪声、增升装置缝翼湍流噪声、发动机喷流噪声、燃烧噪声等问题[10-12]中广泛应用。然而,声源统计方法在噪声产生机理方面以及周期性声学等问题方面有所欠缺。
声传播区域通常可通过求解诸如声扰动方程[11]、线性化欧拉方程[12]、非线性扰动方程[13]等控制方程实现。声传播区域的难点在于如何准确地反映物理波的运动(其中包括涡、声、热等模态)和传播特征(包括色散、耗散、方向、相速度、群速度等)[14-15]。其次,为了准确模拟上述物理波的特性,所使用的离散格式除了具有相容、稳定、高精度的特点,还应该尽可能减小声场相关物理量过多的耗散,并保持各向同性。最后,在声学远场边界,为了避免扰动量产生反射后污染计算域,需要采用数值吸收边界条件(也称为辐射边界,无反射边界等)[16]。这种数值边界起2个作用:①让计算区域内的各种波(声波,涡波,熵波)能无反射地通过边界;②削弱外界扰动污染计算域。到目前为止,为CFD(computational fluid dynamics)而发展的离散格式、边界条件大部分无法直接应用于声传播方程中。因此,发展高精度数值方法越来越重要。
对于混合流致噪声计算方法,另一需要考虑的问题是如何耦合声源计算求解与声传播求解。现有的方法主要分为等效声源法和声波边界条件法[17]。等效声源法是指在传播域中通过对声波传播方程源项求解直接获得,该源项常被认为是噪声的主要来源。源项中的湍流速度可通过大涡模拟等高精度数值方法直接获得,或随机声源模型构造得到。声波边界条件法是指将声源区域的边界作为声传播方程的边界条件。相比于等效声源法,声波边界法应用范围更广,可应用于运动物体的声学问题中。
本文阐述了声扰动方程的数值求解方法(空间离散格式、时间推进格式、边界条件)、声源数据传递方法等。基于声波边界条件思想,改善其使用策略以达到削弱界面处数值伪波问题,从而建立基于声扰动方程和大涡模拟的高精度CAA(computational aero-acoustics)混合数值方法。以NACA0012翼型为研究对象,开展翼型尾缘声源的辐射特性分析研究,通过与试验数据、LES直接计算结果对比分析,验证混合流致噪声预测方法的可行性及准确度。
1 声扰动方程数值方法 1.1 声扰动方程为了得到直接求解声学扰动的控制方程,可以将扰动形式NS方程转化到频率-波数域,对其本征模态进行分离,忽略扰动量的黏性效应,保留仅会激发声学模态响应的部分源项,最后,通过反变换得到时域下的声扰动方程[11]。
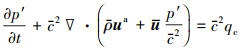
|
(1) |
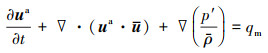
|
(2) |
式中:p′为声压;c为参考声速;ρ为时均流密度;u为时均速度矢量;ua为扰动速度矢量;qc和qm为噪声源项。方程中的时均变量均可通过CFD进行求解。至此, 由(1)~(2)式方程组构成了基本的APE系统。Ewert提出, 根据所面对的不同类型声学问题, 可以对源项采取相应的取舍。APE方程用来描述在非均匀平均流场u基础上的扰动波传播。
1.2 空间离散方法对于声波边界条件方法的应用, 声源区域与传播区域交界处往往存在较强的流场间断问题。为了保证空间离散低耗散、低色散特性, 需在交界处增强数值计算的稳定性。本文空间离散所采用的策略: ①内部网格通量求解采用四阶精度的DRP有限差分格式[15]; ②交界面处通量求解采用WENO改进的有限差分格式, 并选用混合形式的Lax-Friedrichs流通矢量分裂方法进行通量分裂。其中WENO改进格式具体如下:
根据Tam所提出的DRP思想, 对现有的WENO格式进行改善。考虑对流方程∂q/∂t+∂f(q)/∂x=0, 等间距的网格分布xi=iΔx(i=0, …, N), 其半离散格式可表示为
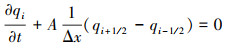
|
(3) |
其中变量常数A=∂f/∂q。
对于5点插值模板, WENO格式的数值通量可通过加权的形式进行表示
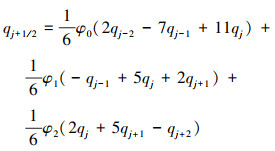
|
(4) |
将(4)式代入(1)式通量项中, 并对傅里叶变换后的方程右端进行泰勒级数展开, 选取五阶精度, 整理可得
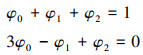
|
(5) |
以φ0作为自由变量, 通过迎风形式的积分误差来进行优化, 积分误差E定义如下
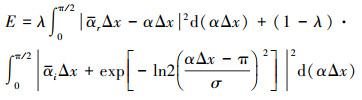
|
(6) |
求(6)式的误差函数的极小值, 可转化为∂E/∂φ0=0的根。表 1给出文中所选用的几组优化系数φ0的具体取值。
| 工况 | λ | φ0 |
| WENO_opt1 | 0.85 | 0.140 6 |
| WENO_opt2 | 0.4 | 0.075 2 |
| WENO_opt3 | 0.1 | 0.020 7 |
| WENO_JS | 0.1 |
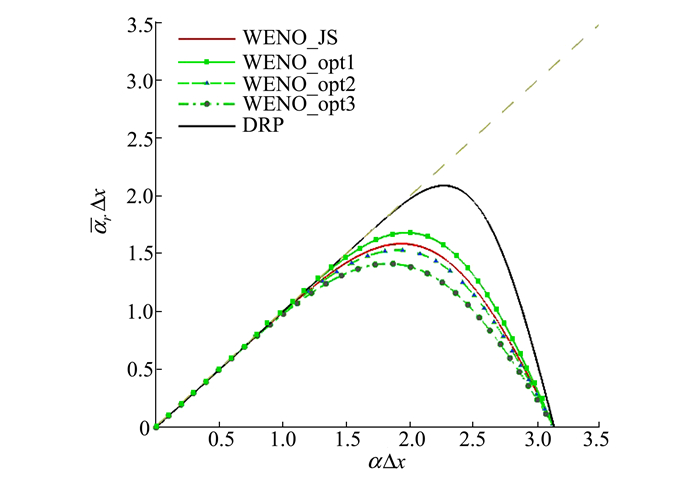
图 1给出了几种不同WENO格式及DRP格式的相位误差特性。从图中可以看出, DRP对声波分辨率最高, 所需网格点数最小。然而, 在交界面处极易出现网格及流场间断现象, 为增加该处的稳定性, 边界处的离散格式选用了色散特性较差但稳定性较高的WENO_opt3格式。
|
| 图 1 不同WENO格式的相位误差特性 |
在APE方程的时间离散方面, 采用了Vasanth等人所提出的大时间步长HALE-RK64格式[18]。以一维偏微分方程为例
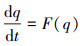
|
(7) |
HALE-RK64格式可表示为:
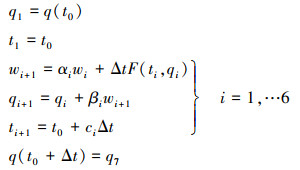
|
(8) |
(8) 式中的参数具体表达式详见文献[18]。
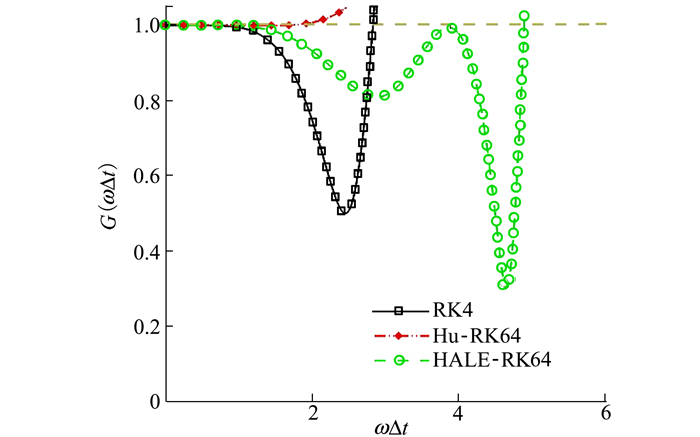
为了说明HALE-RK64时间离散格式在大时间步长下具有较好的稳定性, 根据稳定性特征公式(9), 图 2给出了3种不同时间离散格式的稳定性分析。从图中可以明显看出: HALE-RK64格式的稳定性区域最大, 而相同阶数的Hu-RK64格式[19]稳定性区域最小。

|
(9) |
|
| 图 2 不同时间离散格式的稳定性分析 |
无反射边界条件被人为地划分为计算区域和吸收层, 其作用是使得计算区域内的各种波(声波、涡波、熵波)能无反射地通过边界; 同时让外界的任何扰动都不能传入计算区域。已有的无反射边界条件大致可分为基于特征变量、渐近解、吸收等理念的边界条件。而理想匹配层边界(perfectly matched layer, PML)是一种声反射系数最小的远场边界条件。
本文采用了无分裂形式的理想匹配层边界(PML)条件[20], 其二维表达式具体如下
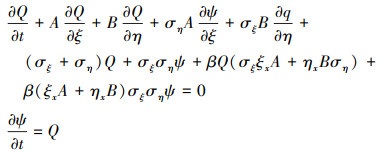
|
(10) |
为了稳定地离散PML边界方程, 本文采用了Gao等[14]提出的DRP7544单侧差分格式, 其表达式具体如下
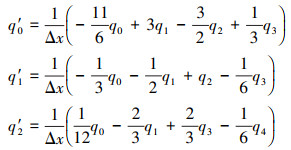
|
(11) |
本文所采用的LES方法计算的控制方程具体如下

|
(12) |
动量方程中亚格子应力采用WALE模型进行计算, 具体表达式如下
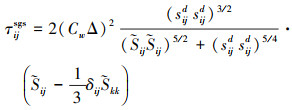
|
(13) |
式中
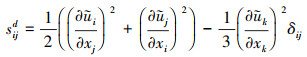
|
除亚格子应力表达式外, 黏性应力张量分量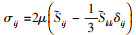
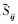
如何快速有效地实现数据从CFD网格到CAA网格的搜索插值,是混合方法预测噪声的一个重要环节。高效网格点搜索和流场插值问题在CAA混合方法中尤为重要,因为每进行一次声场的时间推进均涉及到耦合层的一次插值。本文使用了一种KD树数据结构进行搜索。
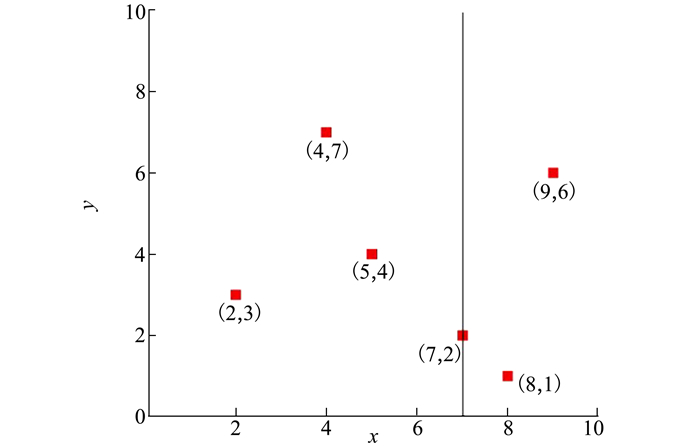
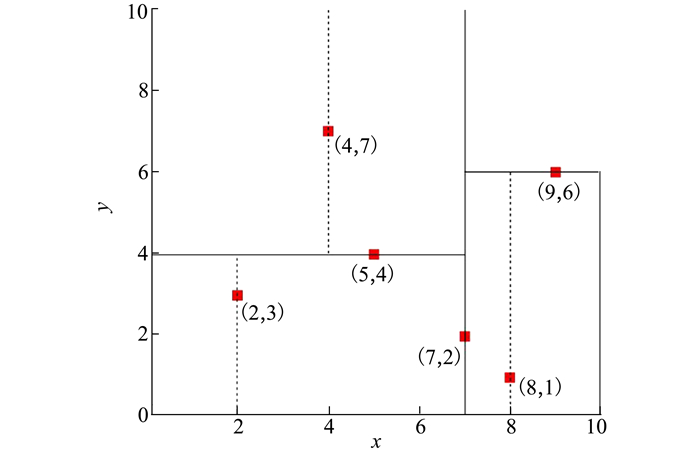
这种方法除了满足全局和高效外,还不要求输入网格的结构性。具体算法主要包括KD树的构造和搜索。以二维平面上的点为例,介绍基于KD树结构的搜索方法。二维平面上有6个点,如图 3所示。根据x, y坐标点的方差统计,x方向方差最大,沿x轴分为2个子区域。对左右子空间重复上述步骤,直到所有子空间中只有一个坐标点形成叶节点。对应的空间划分如图 4所示。
|
| 图 3 KD树算法说明 |
|
| 图 4 空间划分示意图 |
虽然该方法在搜索上是有效的,但在节点的构造上却比较缓慢。在实际应用中,采用场景选择算法来平衡树的构建和搜索树的复杂度。以二维平面中的点(2, 4.5)为例,介绍了二叉树中最近点的查找算法。
通过二叉树搜索,找到子空间。从二叉树的根(7, 2)开始,因为2 < 7,移动到左侧子节点(5, 4)。因为4.5>4,移动到右子节点(4, 7)。按此方法移动,直到当前点是叶节点,停止搜索。
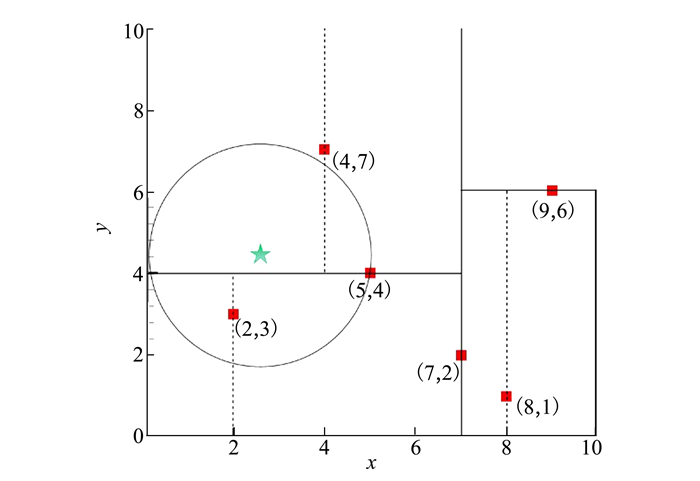
回溯以找到最近的点。首先计算目标点与叶节点(4, 7)之间的距离。然后,沿着搜索路径追溯到父节点(5, 4),并计算其到目标点的距离r。当发现目标点靠近父节点时,以目标点为中心,以距离r为半径,生成圆,如图 5所示。圆与当前节点(4.5, 4)另一侧的子空间相交。而另一侧的子空间中可能会出现最近点,因此需要在另一侧的子空间上重复使用二进制搜索和回溯,直到圆不相交于两边的子空间。此时,找到的节点为目标点的最近点。
|
| 图 5 KD树搜索示意图 |
通过以上分析可以看出,得益于二叉树的数据结构,使用KD树搜索的复杂度为O(lg(n)),具有较高的搜索效率。在完成CAA网格点的搜索后,将采用基于形函数的拉格朗日插值方法进行CFD信息的插值。
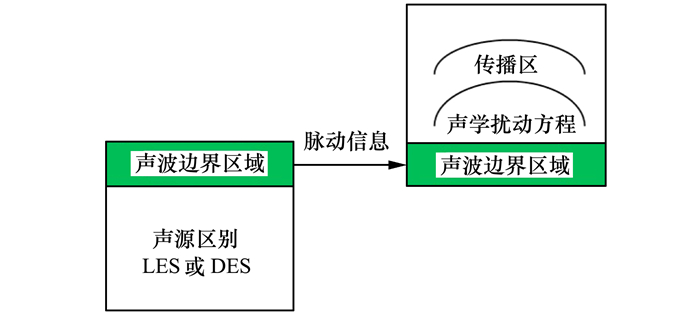
4 基于声波边界条件的混合方法 4.1 混合方法的实施策略声波边界条件法是指将声源区域的外边界作为声传播方程的入口边界条件,具体如图 6所示。在声源求解和声传播的耦合过程中,CFD求解和CAA求解所采用的网格尺度及分布形态有所区别,导致两区域间存在数据插值、时间步长匹配、流场间断等问题。流场间断引起的数值伪波问题将在5.3节进行分析及改善。对于时间步长的匹配问题:CFD计算求解和CAA计算求解时间步长分别为Δt1和Δt2,①当Δt1≤Δt2时,CAA声波边界区域的扰动值将在一个CFD计算时间间隔中线性插值获得;②当Δt1>Δt2时,CAA声波边界区域的扰动值将在3个CFD计算时间间隔中二次曲线插值获得。
|
| 图 6 声波边界条件法的耦合说明 |
1) CFD求解器的数值验证
下面以“槽道中心阻塞率20%的方柱”为研究对象,采用LES方法进行流场计算分析,验证本文所使用CFD求解器的可靠性。数值模拟的计算域及计算条件与Nakagawa等人的试验相似,方柱位于槽道的中央。
在本算例中,基于方柱直径D和来流速度Uinf的雷诺数Re为3 000,流场域的展向尺寸为3D,在入口处使用了完全一致的来流速度Uinf=0.2。在此流动中,柱体下游卡门涡街的发展将受到壁面的严重影响,而近壁面流动结构也会受到卡门涡街的影响。
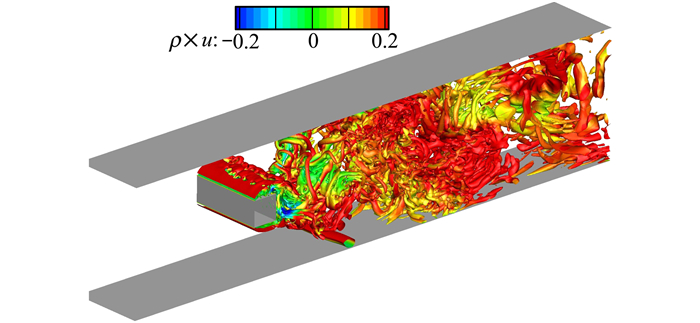
图 7给出了Q=0.05的等值面图,从图中可以看出方柱后面脱落出复杂的涡系。
|
| 图 7 Q=0.05等值面图(采用流向速度守恒变量着色) |
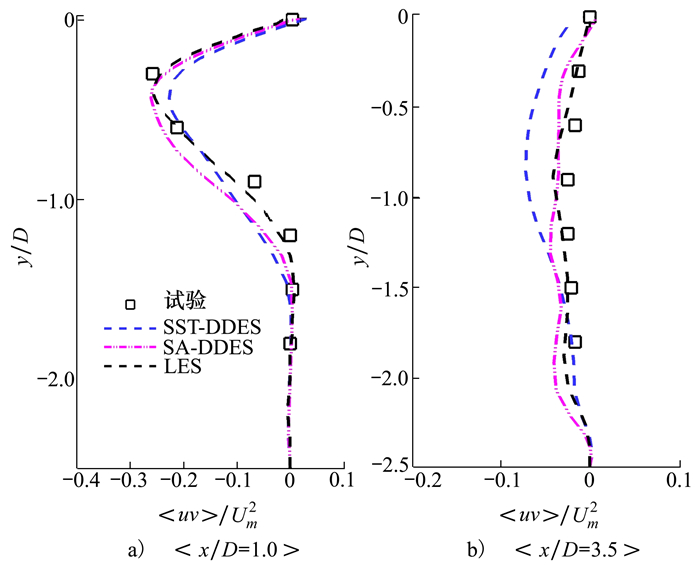
图 8给出了x/D=1.0, 3.5站位处的雷诺应力曲线对比结构,从图中可以看出,相比于DES方法,LES方法与试验数据更吻合。
|
| 图 8 雷诺应力分布图(x/D=1.0, 3.5) |
2) CAA求解器的数值验证
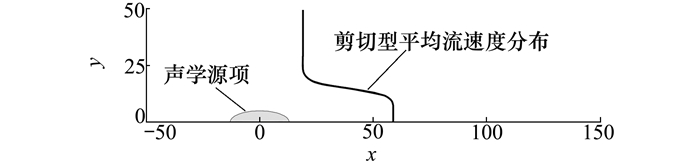
本算例为第四届CAA基准算例研讨会[1]中的二维声波穿过剪切层后的辐射与折射现象,用来验证扰动方程的数值特性与边界条件的正确性。对于平行射流剪切层问题,其平均流中包含了黏性和非线性效应。
计算域为[-50, 150]m×[0, 50]m的矩形区域。在计算域下方设置对称面边界,其余3个方向设置PML边界条件。网格内点与内边界处空间离散都使用了7点DRP-WENO格式,时间推进使用HALE-RK64格式,无量纲时间步长为Δt=0.2。
|
| 图 9 射流剪切层问题的计算条件示意 |
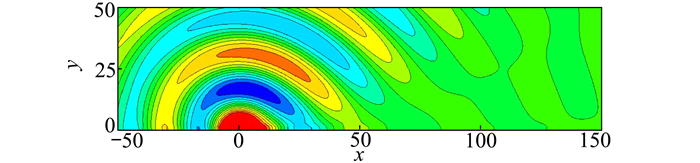
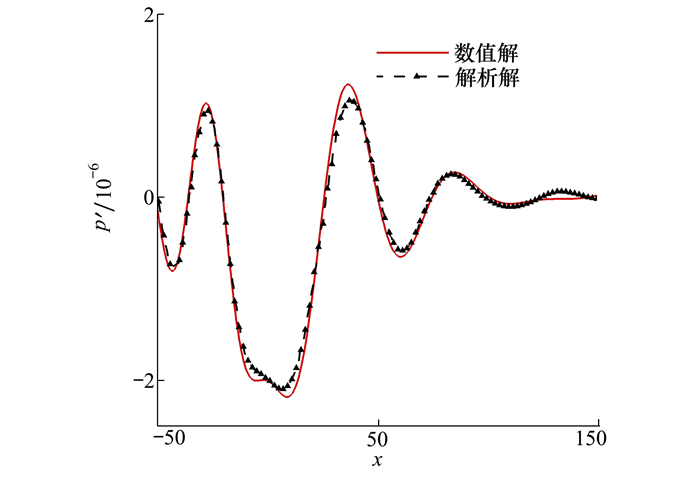
图 10为t=12T时刻的扰动压力场模拟结果,T为声源周期。为更细致比较各状态间的差异,图 11给出了t=12T时刻y=15上的扰动压力结果对比,其压力曲线计算解与解析解基本吻合,验证了声传播控制方程数值离散方法的准确性与可行性。
|
| 图 10 t=12T时刻的射流问题扰动压力分布等值线云图 |
|
| 图 11 t=12T时刻y=15的扰动压力曲线 |
为了开展翼型的声辐射特性研究,选取了BANC(benchmark problems for airframe noise computations)试验中的NACA0012[21]作为研究对象。NACA0012翼型试验的参考弦长为0.4 m,单位尺度雷诺数为3.83×106,转捩位置、来流速度、迎角分别如表 2所示,其中SS为翼型吸力面转捩位置,PS为翼型压力面转捩位置。计算条件与试验条件保持一致。
CFD网格及CAA网格分布如图 12所示,其中CFD网格量为80万左右,为了有效模拟附面层的流动特征,其网格尺度分布保证了y+ < 1的数值计算要求,此外在翼型尾缘分离流区域进行了局部网格加密处理。而CAA网格在附面层附近则更加注重网格的正交性及长细比分布要求,整体网格的分布尺度满足一个波长所需的网格点数需求,网格量为100万左右。

|
| 图 12 计算网格分布 |
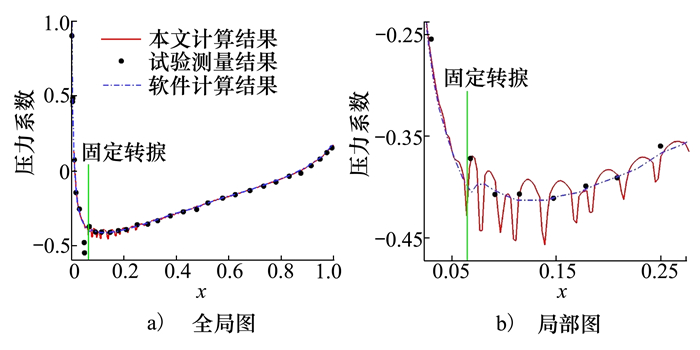
为了定量对比数值计算结果的准确性,图 13给出了翼型表面压力系数分布对比曲线图。图中红色线为本文计算结果,黑色实心圆点为试验测量结果[21],蓝色虚线为Xfoil软件计算结果,绿色直线位置为试验固定转捩点位置。从全局图中可看出:本文所计算的压力系数分布可看出转捩位置附近有明显的振荡现象。
|
| 图 13 压力系数分布对比 |
当获得定常状态解后,将其作为初始流场进行LES非定常计算,其无量纲时间步长为0.005。待计算收敛后,进行非定常源项变量的采样,采样步数30 000。
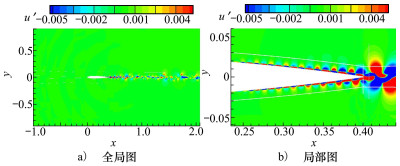
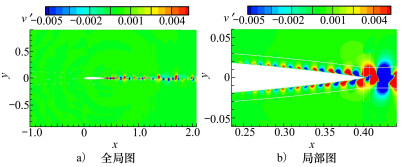
图 14为非定常计算求解获得的流向脉动速度分布云图,图 15为法向脉动速度分布云图。其中,CFD脉动速度变量通过瞬时流场速度变量减去时均流场速度变量获得。从这两幅云图中可看出:①流向和法向的脉动速度主要分布于翼型的尾缘及尾流区;②流向脉动速度在尾缘上下端面呈近似对称形态,尾流区呈正负交叉形态;③法向脉动速度在尾缘上下端面呈近似正负交替的对称形态,尾流区呈正负交替形态。④法向脉动速度的强度明显大于流向脉动速度,这与升阻力系数曲线的幅值大小表现一致。
|
| 图 14 流向脉动速度分布 |
|
| 图 15 法向脉动速度分布 |
基于CFD/CAA混合方法是将整个计算域分成声源产生区域和声传播区域2个部分。其中声源区计算采用LES数值方法进行计算求解,传播区采用声扰动方程求解,计算时间步长与LES非定常计算步长保持一致,初始的声源区域选取如图 16所示。初始的声源区选取范围主要依靠Lamb矢量分布范围来决定,本文选取了包含90%Lamb矢量大小的区域。两计算区域的耦合采用了声波边界条件法。

|
| 图 16 初始的声源区域选取方式 |
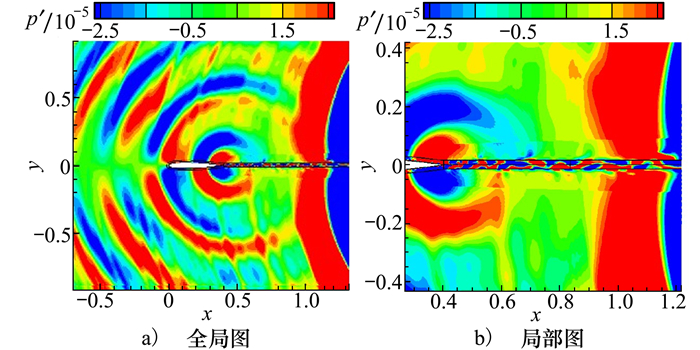
图 17为采用图 16声源区域选取方式所获得的声压云图, 从图中可以看出存在大量的数值伪波现象,这主要是由声波穿过强流场间断所引起的不稳定扩散导致[22]。
|
| 图 17 CFD/CAA求解的声压云图 |
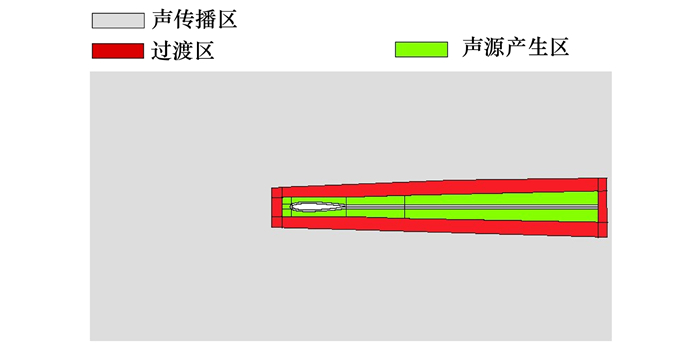
为解决上述现象,文中主要采取两方面的措施:一方面将声源区边界范围扩大至95%Lamb矢量大小区域,减小声源区边界穿越尾流分离区;另一方面,为了减小声源区与传播区因声源变量间断引起的短波发散问题,可在初始步赋值时,添加人工过渡层,如图 18所示。其中,灰色区域为声传播区域,绿色区域为声源区域,红色区域为过渡区域。过渡区域采用的函数是以距离为变量的半高斯函数。
|
| 图 18 改进的声源区域选取方式 |
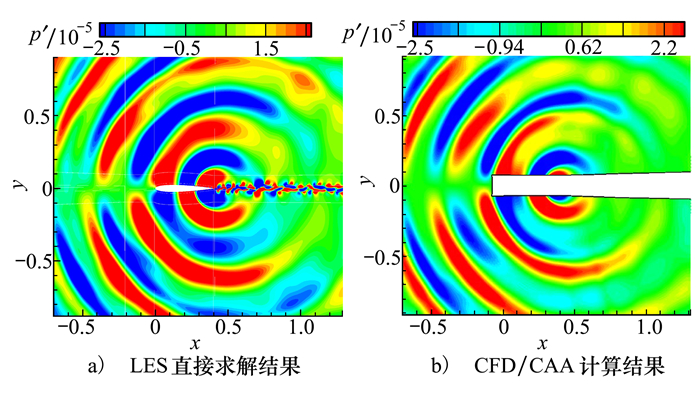
图 19显示了某时刻瞬时声压分布云图,图 19a)为采用项目组自编程序LES直接模拟求解所获得的声场分布,图 19b)为基于声波边界条件的CFD/CAA混合方法计算结果。从声压云图中可以看出,2种方法所获得声压云图分布形态及大小基本一致,均呈现沿y=0的对称分布形态。此外,从图 19a)中可看出:翼型的尾缘噪声主要是由尾缘处上下翼面正负交替的涡作用产生。
|
| 图 19 瞬时时刻声压云图 |
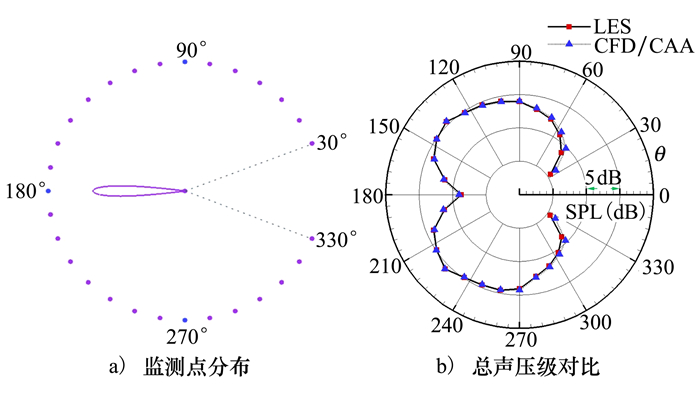
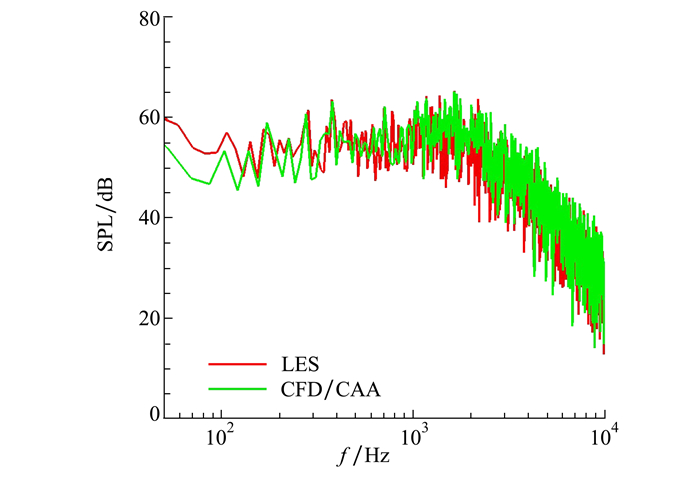
图 20为分别采用LES直接计算与CFD/CAA方法计算的噪声指向性对比图。由图可以看出,采用全场LES直接计算和CFD/CAA混合方法得到的指向性曲线基本重合,误差不超过2 dB,声波主要强度位于1 200到1 500区域。造成两者误差的可能原因:传播区域LES方法和CFD/CAA方法的网格分布、数值离散方法均有所区别,此外声源区的位置选取也可能有一定影响。总的来说,该结果表明基于声波边界条件的流致噪声混合方法可准确预测尾缘噪声问题。图 21给出了位于翼型后缘正上方(900)1.5倍翼型参考弦长处的声压级频谱曲线对比结果。通过对比可看出:两者计算结果趋势和声压级量级基本相当,最大声压级相差1 dB左右。
|
| 图 20 噪声指向性对比 |
|
| 图 21 1/3倍频声压级频谱曲线 |
本文开展了基于声扰动方程的流致噪声混合方法的研究分析,并对混合方法中的各模块进行了验证分析。在此基础上,以二维NACA0012翼型为研究对象,分析了其声学辐射特性,具体结论如下:
1) 本文所建立的基于声扰动方程的混合预测方法,能够高精度地预测流致噪声问题中的声辐射特征,并直观反映声波与声波之间的相互作用现象及空间分布特征。
2) 对于本文所提及的CFD/CAA混合方法,声源区的边界应避免位于尾流的强扰动中。此外,为了减小声源区与传播区间的声波间断问题,初始步可通过引入阻尼层达到顺利过渡的作用。
3) 从翼型尾缘的噪声源地分布特点可看出,声源的分布位置与旋涡的分布位置基本保持一致。翼型的尾缘噪声主要是由尾缘处上下翼面正负交替的涡作用产生。
4) 在声波的相互作用及与壁面的作用下,翼型噪声的指向性主要呈现偶极子特征,主要强度位于120°~150°区域。
5) 基于声波边界条件方法的高精度流致噪声计算方法由于声源求解和声传播求解区域部分重合特性,后续有望将该方法应用于类似扑翼、螺旋桨等噪声问题中。
| [1] | THOMAS N L, VINCENT F A, YVES D. CFD/CAA coupling strategies for rearward fan noise[R]. AIAA-2018-4089 |
| [2] | LABAN M, KOK J C, BROUWER H H. CFD/CAA analysis of UHBR engine tonal noise[R]. AIAA-2018-3780 |
| [3] | ANSGAR N, MATHIAS M, WOLFGANG S, et al. Noise reduction using a direct-hybrid CFD/CAA method[R]. AIAA-2019-2579 |
| [4] | TERRACOL M, MANOHA E, HERRERO C, et al. Hybrid methods for airframe noise numerical prediction[J]. Theoretical and Computational Fluid Dynamics, 2005, 19(3): 197-227. DOI:10.1007/s00162-005-0165-5 |
| [5] | BERNICKE P, AKKERMANS R A D. Overset LES for trailing-edge noise computations[R]. AIAA-2017-3170 |
| [6] | ZHANG Y F, CHEN H X. Aeroacoustic prediction of a multi-element airfoil using wall-modeled large-eddy simulation[J]. AIAA Journal, 2017, 55(12): 4219-4233. DOI:10.2514/1.J055853 |
| [7] |
魏佳云, 李伟鹏, 许思为, 等. 基于DMD方法的缝翼低频噪声机理分析[J]. 航空学报, 2018, 39(1): 121469.
WEI Jiayun, LI Weipeng, XU Siwei, et al. Analysis of mechanism of slat low frequency noise based on zonal DMD[J]. Acta Aeronautica er Astronautica Sinica, 2018, 39(1): 121469. (in Chinese) |
| [8] | YAO H D, DAVIDSON L. Assessment of conceptual noise reduction devices for a main landing gear using SNGR method[R]. AIAA-2015-2692 |
| [9] |
余培汛, 潘凯, 白俊强, 等. 快速随机粒子网格法的气动噪声预测方法[J]. 声学学报, 2018, 12(5): 817-828.
YU Peixun, PAN Kai, BAI Junqiang, et al. Computational aero-acoustics prediction method based on fast random particle mesh[J]. Acta Acustica, 2018, 12(5): 817-828. (in Chinese) |
| [10] | HAN X, YU P X, BAI J Q, et al. Hybrid computational aeroacoustics approach based on the synthetic turbulence model in eulerian description[J]. Aerospace Science and Technology, 2020, 106: 106077. DOI:10.1016/j.ast.2020.106077 |
| [11] |
陈荣钱, 伍贻兆, 夏健. 基于SNGR方法的二维空腔噪声数值模拟[J]. 南京航空航天大学学报, 2012, 41(1): 56-60.
CHEN Rongqian, WU Yizhao, XIA Jian. Numerical simulation of two-dimensional cavity noise by SNGR method[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 41(1): 56-60. (in Chinese) DOI:10.3969/j.issn.1005-2615.2012.01.010 |
| [12] |
吕宏强, 朱国祥, 宋江勇, 等. 线化欧拉方程的高阶间断有限元数值解法研究[J]. 力学学报, 2011, 43(3): 611-624.
LYU Hongqiang, ZHU Guoxiang, SONG Jiangyong, et al. High-order discontinuous galerkin solution of linearized Euler equations[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(3): 611-624. (in Chinese) |
| [13] | EWERT R, DIERKE J, NEIFELD A. Linear and non-linear perturbation equations with relaxation source terms for forced eddy simulation of aeroacoustic sound generation[R]. AIAA-2014-3053 |
| [14] | GAO J H, LI X D. Improved grid block interface flux reconstruction method for high-order finite difference scheme[J]. AIAA Journal, 2005, 53(7): 1761-1773. |
| [15] | YU P X, BAI J Q, PAN K. Interface flux reconstruction method based on optimized weight essentially non-oscillatory scheme[J]. Chinese Journal of Aeronautics, 2018, 31(5): 1020-1029. DOI:10.1016/j.cja.2018.02.012 |
| [16] | OVAIS U K, GHULAM A. Simulation of acoustic radiations over an open cavity using high-resolution numerical scheme[R]. AIAA-2020-1750 |
| [17] | TERRACOL M, MANOHA E, HERRERO C, et al. Hybrid methods for airframe noise numerical prediction[J]. Theoretical and Computational Fluid Dynamics, 2005, 19: 197-227. |
| [18] | VASANTH A, RAY H. High-accuracy large-step explicit Runge-Kutta(HALE-RK) schemes for computational aeroacoustics[J]. Journal of Computational Physics, 2009, 228: 3837-3850. |
| [19] | HU F Q, HUSSAIN M Y. Low dissipation and dispersion Runge-Kutta schemes for computation acoustics[J]. Journal of Computational Physics, 1996, 124(1): 177-191. |
| [20] | TAM C K W, AURIAULT L. Perfectly matched layer as absorbing boundary condition for the linearized euler equations in open and ducted domains[R]. AIAA-2001-0217 |
| [21] | SEONGKYU L, JESSICA G S. Prediction of airfoil trailing-edge noise using empirical wall-pressure spectrum models[J]. AIAA Journal, 2019, 57(3): 888-897. |
| [22] | BROOK P. Fourth computational aeroacoustics(CAA) workshop on benchmark problems[R]. NASA/CP-2004-212954 |
2. Xi'an Precision Machinery Researh Institute, Xi'an 710077, China;
3. School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China




