2. 西北工业大学 航空学院, 陕西 西安 710072
生物组织和水凝胶等可膨胀软材料, 具有许多突出的性能, 比如对外界刺激的敏感性、大变形和可逆变形的能力以及离子导电性等。基于这些特性, 它们已被应用于许多工程领域[1]。叶子、花瓣等软生物组织的增长是常见的自然现象。增长场的不均匀性和不兼容性, 使得这些生物软组织发生几何形状和形态模式上的改变[2]。为了刻画软材料增长的动力学和热力学过程, Ganghoffer[3]提出了基于无应力构型的连续增长理论, 将变形前后构型的映射分解成增长映射和弹性映射, 即变形梯度乘法分解成弹性部分和增长部分。基于变形梯度的乘法分解, 学者们建立了相应的数值求解框架, 采用数值方法对生物软组织和水凝胶的增长进行了研究。
Wang等[1]借助非均匀有理B样条单元, 建立了模拟可膨胀软材料增长的等几何计算框架。这个计算框架在分析仿生结构和设计仿生器件的力学行为方面也具有很大的潜力。Zheng和Wang等[4-5]提出了基于实体-壳单元的非线性有限元框架来对薄壁软结构的增长以及含增强纤维的水凝胶各向异性膨胀进行数值分析。Kadapa等[2]基于高阶单元建立了混合有限元框架来模拟可压缩和不可压缩软材料的增长和变形。
然而软材料增长的数值模拟会涉及大变形, 采用有限元等方法求解会出现网格畸变使得迭代求解过程出现发散(数值奇异)。为了有效地改善这一情况, 需采用基于欧拉描述的无网格方法或其他对网格畸变不敏感的数值方法来对软材料的增长过程进行模拟。
光滑有限元方法相比传统有限元方法, 不需要对任意形状的网格单元进行等参变换, 将体(面)积分转化成面(线)积分, 对网格畸变具有一定免疫性, 在模拟大变形方面更具优势。此外, 光滑有限元方法从理论上被证明拥有比传统有限元方法更小的刚度, 因而精确性更高[6-9]。
单元域光滑有限元(cell-based smoothed finite element method, CS-FEM)是光滑有限元方法的一种, 它将每个有限元单元划分成若干个cell, 并将各个cell定义成光滑域。由于CS-FEM不存在跨网格操作, 并且每个光滑域支撑点的个数相等, 在程序实现和总体刚度矩阵的稀疏化处理上更为便捷。本文基于CS-FEM建立了可膨胀软材料增长的数值框架, 通过对软材料在不同条件下增长行为的模拟验证该数值方法的有效性。
1 基本理论 1.1 变形梯度的乘法分解和变形张量变形前后初始构型Ωo和当前构型Ωc之间的映射可以用变形梯度F来描述, 其定义为

|
(1) |
根据文献[10]的处理方法, 变形梯度可以分解成弹性变形梯度Fe和增长张量Fg
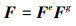
|
(2) |
变形体在Fg的作用下, 从初始构型转化到中间构型, 然后在Fe的作用下, 由中间构型转换到当前构型, 如图 1所示。变形梯度行列式J可以表示变形前后体积微元的相对变化, 根据(2)式有

|
(3) |

|
| 图 1 增长时的构型变化 |
由(2)式和右柯西-格林应变张量的定义, 可以得到右柯西-格林应变张量Ce的表达式
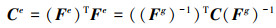
|
(4) |
根据文献[2]的做法, 增长变形过程中的总势能泛函可以表示成中间构型Ωm下弹性应变能密度ψe的积分[11]
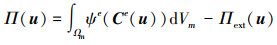
|
(5) |
式中:Πext分别表示外力势能泛函;dVm表示中间构型的积分体元。中间构型与初始构型的积分体元存在(6)式所示关系
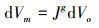
|
(6) |
因此, 总势能泛函可以表示成

|
(7) |
为了推导位移场的控制方程, 将(7)式代入位移场的欧拉-拉格朗日方程
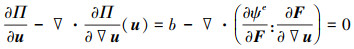
|
(8) |
式“: ”表示张量的缩并, b表示体力。根据超弹性材料的本构方程和变形梯度的定义, (8)式可以进一步表示成

|
(9) |
式中,P为第一Piola-Kichhoff(P-K)应力张量。为了推导和表示方便, 将(9)式写成分量和下标形式
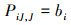
|
(10) |
本节字母大写表示初始构型的坐标分量,小写表示当前构型的坐标分量。除控制方程外, 还须满足以下边界条件
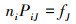
|
(11) |
式中,ni为初始构型面力作用积分面元法向量的分量, fJ表示面力分量。对(7)式求变分可以得到
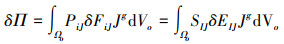
|
(12) |
式中,EIJ为格林应变张量的分量, 其具体表达式为

|
(13) |
式中,δIJ为二阶单位张量的分量, 下标p为哑标。(12)式即为位移场控制方程的弱形式, 对其进行线性化, 有
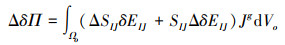
|
(14) |
由于弹性自由能ψe是弹性变形张量的函数, 所以第二P-K应力分量S和第二P-K弹性应力分量之间存在如下关系
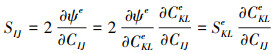
|
(15) |
将(4)式代入(15)式右边项可以进一步得到
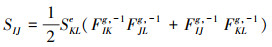
|
(16) |
由(15)式可以得到第二P-K应力增量ΔSIJ的表达式
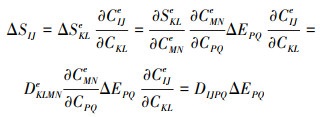
|
(17) |
式中:DKLMNe为四阶弹性本构张量的分量;DIJPQ为四阶本构张量的分量, 它们存在如下关系

|
(18) |
式中,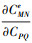

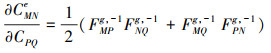
|
(19) |
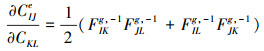
|
(20) |
由(13)式δEIJ可以表示为
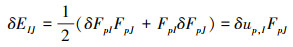
|
(21) |
由于位移梯度的虚增量δup, I, δup, J是小量, 再对其取增量, 便可忽略。于是可以得到ΔδEIJ的表达式
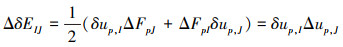
|
(22) |
在三维CS-FEM中, 将八节点六面体单元划分成8个光滑域, 如图 2所示。并给出了光滑域内光滑位移梯度的定义

|
(23) |

|
| 图 2 三维CS-FEM光滑域的划分 |
式中:xC表示光滑域中心的坐标; ΩC表示光滑域; Vc表示光滑域的体积。应用散度定理可以将(23)式的体积分转化成面积分, 有

|
(24) |
式中,ΓC表示光滑域的外表面, 在图 2中表示六面体光滑域的6个表面。光滑域中心的位移场可由该光滑域支撑点位移场通过中心处形函数插值得到, 可以将(24)式进一步表示为
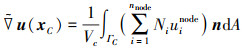
|
(25) |
根据应变位移矩阵B的定义以及积分和求和算符的可互易性, 将各个光滑域对节点i的B矩阵表示成光滑域各个表面高斯积分的形式, 如下所示
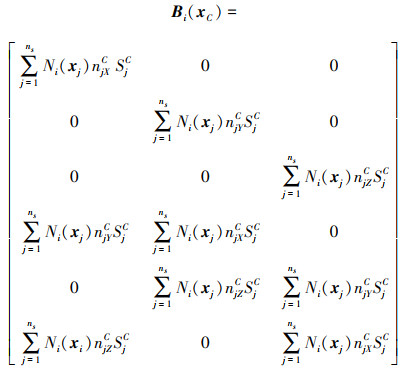
|
(26) |
式中:nS为光滑域积分面的数目; Ni(xj)表示第j个积分面的高斯点对节点i的形函数; njXC, njYC, njZC分别表示第j个积分面外法线的分量; SjC表示第j个积分面的面积。在这里, 选取这个积分面的中心为高斯点。
2 基于CS-FEM的三维增长数值框架为了模拟软材料增长过程, 需要对(9)式中的位移控制方程进行数值求解。由于位移控制方程是非线性的, 需要得到控制方程的弱形式及其线性化后的表达形式来构建非线性数值框架。为了构建CS-FEM求解位移场的数值框架, 需对(12)式中的弱形式和(14)式中弱形式线性化后的表达式进行离散。首先需将光滑域中位移虚增量δu和位移增量Δu离散成如下形式
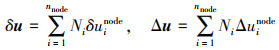
|
(27) |
为了表达方便, 需借助Voigt规则将二阶张量S和δE表示成矢量形式, 如下所示
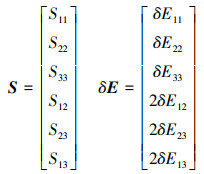
|
(28) |
由(20)式和(25)式, 可以将(28)式中δE进一步离散成

|
(29) |
同理ΔE可以离散成

|
(30) |
将(27)~(28)式代入(12)式中, 并两边同除以δunode可得到位移场残差力Riu(xC)的表达式
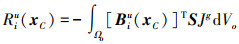
|
(31) |
同理可以将(14)式中右边第二项离散成
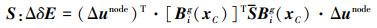
|
(32) |
(32) 式Big(xC)的分量表达式为

|
(33) |
S的分量表达式为

|
(34) |
在对(14)式中右边第一项进行离散化时, 需要得到(18)式中DKLMNe的表达式, 同时有必要将本构张量D写成矩阵形式。本文选用Neo-Hookean本构模型, 它的弹性能密度ψe表达式为
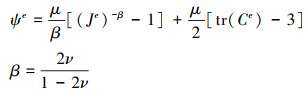
|
(35) |
对应的第二P-K弹性应力张量SIJe的表达式为

|
(36) |
对应的四阶弹性本构张量DIJKLe的表达式为
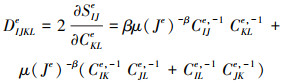
|
(37) |
将(37)式代入(18)式便可得到本构张量D的分量表达式, 并将其转化成如下矩阵形式
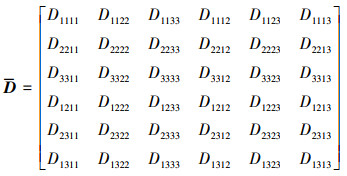
|
(38) |
可以将(14)式中右边第一项离散成

|
(39) |
综上可以得到位移场刚度矩阵Kiu(xC)的表达式

|
(40) |
(40) 式右边第一项为材料刚度矩阵, 表示材料的非线性; 右边第二项为几何刚度矩阵, 表示大变形下的几何非线性。将(31)式中的残差力和(40)式中的刚度矩阵进行组装, 可以得到总体残差力r和总体刚度矩阵K, 然后采用牛顿迭代法对位移场进行求解, 如下所示

|
(41) |
(41) 式中下标表示加载步。
3 数值算例在这一节, 为了验证建立的CS-FEM数值框架在模拟增长导致变形上的鲁棒性, 选用了3个自然界和日常生活的增长问题作为数值算例。这3个模型的网格和节点信息均借助有限元商业软件Abaqus生成。对应的inp文件导进CS-FEM的Matlab程序中, 来获取网格和节点信息。为了减少计算量, 本节的2个算例均采用四分之一模型来进行计算。在输出云图时, 根据网格节点坐标和位移场的对称性, 对模型进行了补全。
3.1 花瓣增长花瓣几何形状如图 3所示, 其厚度为0.3 cm, 底部正方形中心区域被固定。为了实现增长诱导变形, 将花瓣沿厚度方向分成主动层和被动层, 其中主动层靠近模型底端, 厚度为0.1 cm; 被动层厚度为0.2 cm。被动层材料剪切模量为3 571.43 MPa, 泊松比为0.38。主动层材料剪切模量为357.143 MPa, 泊松比为0.38。用Abaqus将花瓣模型的四分之一划分成432个六面体单元, 如图 4所示。对2个剖分面上的节点施加对称边界条件。

|
| 图 3 花瓣的几何形状 |

|
| 图 4 花瓣四分之一模型的网格划分 |
该算例采用2种增长张量: 各向同性增长张量和各向异性增长张量。前者主对角线元素相等, 其他分量都为0;后者Y, Z轴方向的主对角线元素相等并且与X轴的增长方向相反, 其他分量都为0。本文设定Y, Z轴方向的增长为正向增长量, 使其随时间不断增加。并且模拟得到的结果与文献[2]中的数值结果进行了比较。
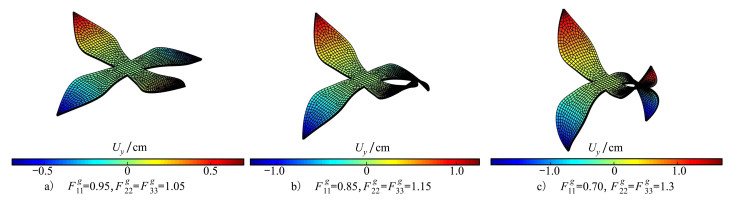
模拟结果显示, 在各向同性增长张量作用下, 主动层的单元带动被动层的单元不断向Z轴正方向弯曲, 最后聚拢在中心处上方, 当前构型下沿Z轴方向的位移云图如图 5所示。在各向异性增长张量的作用下, 沿Y轴方向铺展的花瓣向Z轴负方向弯曲, 沿X轴方向铺展的花瓣向Z轴正方向弯曲, 并且其Z轴方向的位移场呈反对称分布, 如图 6所示。比较图 5和图 6可以发现, 各向异性的增长变形幅值明显小于各向同性, 这一特征与文献[2]中的数值结果吻合。

|
| 图 5 当前构型下沿Z轴方向的位移云图(各向同性) |
|
| 图 6 当前构型下沿Z轴方向的位移云图(各向异性) |
本节研究超弹性圆杆增长至不同的构型。圆杆底圆半径为0.025 cm, 圆杆长度为4 cm。圆杆剪切模量和泊松比分别为588 MPa和0.42。对圆杆Z=0的圆面施加固定约束, 并设置圆杆所有区域为增长张量的影响区。采用Abaqus对圆杆进行网格划分生成2 632个六面体单元, 如图 7所示。

|
| 图 7 圆杆的网格划分 |
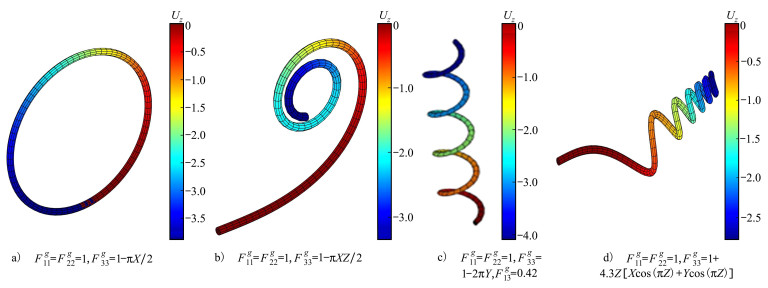
本节假定圆杆只有Z轴方向的主增长分量, 按照文献[2, 12]的做法, 将Z轴方向的主增长分量设置成初始坐标的函数。采用建立的软材料增长的CS-FEM数值框架, 对应不同的增长张量进行模拟, 模拟结果如图 8所示。在图 8中, 直圆杆在不同增长张量的作用下分别变形至圆形、海螺形、等距螺旋形、非等距螺旋形。模拟结果与文献[2]中的数值结果吻合较好, 验证了所建立的CS-FEM框架模拟软材料增长大变形问题的有效性。
|
| 图 8 圆杆在当前构型下Z轴方向的位移场云图 |
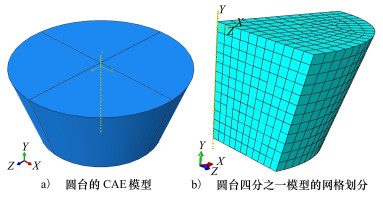
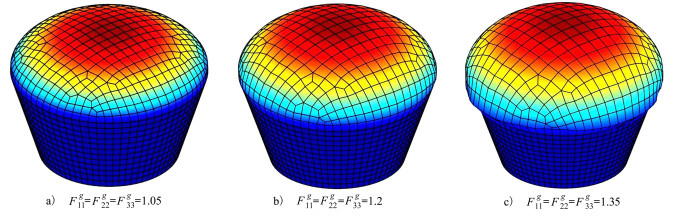
本节选用圆台为研究对象, 其CAE模型如图 9a)所示。该圆台底圆和顶圆半径分别为3.5 cm和2.5 cm, 高为3 cm。选取圆台的四分之一来进行数值模拟, 对底面和圆台侧面施加固定约束, 对内剖面施加对称位移约束。采用Abaqus对圆台四分之一模型进行网格划分, 单元模型如图 9b)所示。让图 9b)中的所有单元受各向同性增长张量的影响。材料的剪切模量和泊松比分别为385 MPa和0.45。使增长张量的分量随加载步均匀增加, 模拟得到圆台当前构型的变化如图 10所示。
|
| 图 9 几何形状和单元划分 |
|
| 图 10 圆台的各向同性增长 |
在图 10中, 圆台在增长张量的激励和底部以及侧面的约束作用下, 只能沿Y轴正方向发生变形, 在构型上表现为圆台向上鼓起。随着增长张量的不断增加, 鼓起部分的网格将沿X-Z平面发生径向均匀膨胀, 最终将超过圆台顶部的边界。这一增长现象和泡芙的制作过程较为吻合。
4 结论本文基于变形梯度的乘法分解, 选用第二P-K应力张量和格林应变张量, 首次建立了CS-FEM模拟可膨胀软材料在大变形下增长行为的数值框架, 给出了材料刚度矩阵和几何刚度矩阵的光滑有限元表达形式, 模拟了可膨胀软材料在各向同性、各向异性增长张量作用下的增长行为, 模拟结果和已有文献中的数值结果进行了对比。模拟结果中构型的变化规律和特征与已有文献中的结果吻合较好。模拟结果发现:
1) 在相同的增长分量情况下, 各向异性增长激励可膨胀软材料的变形相比各向同性增长更小。
2) 对于各向异性增长行为, 通过设置增长张量分量关于坐标的函数形式, 可以调节软材料的增长形态。
3) 本文建立的CS-FEM数值框架可以有效地模拟可膨胀软材料的大变形增长行为, 可以帮助揭示自然界中花瓣、植物茎生长现象和生活中泡芙制作过程的力学机理。
| [1] | WANG Jianhua, ZHANG Hongwu, ZHENG Yonggang, et al. High-order NURBS elements based isogeometric formulation for swellable soft materials[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 363: 112901. DOI:10.1016/j.cma.2020.112901 |
| [2] | KADAPA C, LI Z F, HOSSAIN M, et al. On the advantages of mixed formulation and higher-order elements for computational morphoelasticity[J]. Journal of the Mechanics and Physics of Solids, 2021, 148: 104289. DOI:10.1016/j.jmps.2020.104289 |
| [3] | GANGHOFFER J F. A kinematically and thermodynamically consistent volumetric growth model based on the stress-free configuration[J]. International Journal of Solids and Structures, 2013, 50: 3446-3459. DOI:10.1016/j.ijsolstr.2013.06.011 |
| [4] | ZHENG Yonggang, WANG Jianhua, YE Hongfei, et al. A solid-shell based finite element model for thin-walled soft structures with a growing mass[J]. International Journal of Solids and Structures, 2019, 163: 87-101. DOI:10.1016/j.ijsolstr.2018.12.024 |
| [5] | WANG Jianhua, QIU Yisong, ZHANG Hongwu, et al. A solid-shell finite element method for the anisotropic swelling of hydrogels with reinforced fibers[J]. European Journal of Mechanics-A/Solids, 2021, 86: 104197. DOI:10.1016/j.euromechsol.2020.104197 |
| [6] | LIU G, DAI K Y, NGUYEN T T. A smoothed finite element method for mechanics problems[J]. Computational Mechanics, 2006, 39(6): 859-877. |
| [7] | ZENG Wei, LIU Guirong, JIANG Chen, et al. An effective fracture analysis method based on the virtual crack closure-integral technique implemented in CS-FEM[J]. Applied Mathematical Modelling, 2016, 40(5): 3783-3800. |
| [8] | LIU G, NGUYEN X H, NGUYEN T T. A theoretical study on the smoothed FEM(S-FEM) models: properties, accuracy and convergence rates[J]. International Journal for Numerical Methods in Engineering, 2010, 84(10): 1222-1256. DOI:10.1002/nme.2941 |
| [9] | ZENG W, LIU G R. Smoothed finite element methods (S-FEM): an overview and recent developments[J]. Archives of Computational Methods in Engineering, 2018, 25: 397-435. DOI:10.1007/s11831-016-9202-3 |
| [10] | RODRIGUEZ A K, HOGER A, MCCULLOCH A. Stress-dependent finite growth in soft elastic tissue[J]. Journal of Biomechanics, 1994, 27: 455-467. DOI:10.1016/0021-9290(94)90021-3 |
| [11] | KUHL E. Growing matter: a review of growth in living systems[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2014, 29: 529-543. DOI:10.1016/j.jmbbm.2013.10.009 |
| [12] | MOULTON D E, LESSINNES T, GORIELY A. Morphoelastic rods. Part Ⅰ: a single growing elastic rod[J]. Journal of the Mechanics and Physics of Solids, 2013, 61: 398-427. |
2. School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China




