波达方向估计(direction of arrival, DOA)是阵列信号处理研究的一个主要关切,测定信源方向不仅是实现目标定位乃至跟踪的基础,还能为接收端信号增强提供支持,其应用十分广泛,涉及雷达、通信、声呐、传感网、无人机、医学成像、智能驾驶等诸多领域[1-3]。在远场环境下,阵列天线的DOA估计精度一般正比于有效孔径,且不等间隔方式配置阵元可产生更丰富的阵元间距,于是在分辨率和自由度方面稀疏线阵都要优于传统的最小间距均匀线阵(uniform linear array, ULA),因而稀疏阵的相关研究数十年来受到了持续关注[4]。许多稀疏阵列[5-7]能够利用N个物理阵元获得长度为O(N2)的中央连续段差分共阵,理论上可以估计O(N2)个不相关的信源角度。但在实际应用中,恶劣的环境、人为干扰、阵元老化等因素都可能引发阵元随机故障,会导致中央连续段差分共阵变短继而使阵列性能受损[6, 8]。合理的阵列几何结构使相同数目的物理阵元在经受随机故障时能达成更好的DOA估计效果。因此,设计在阵元随机故障条件下具有高鲁棒性,保持较长中央连续段差分共阵的稀疏阵列是一个颇有价值的课题[9-10]。
于20世纪60年代提出的典型稀疏线阵包括最小冗余阵(minimum redundancy arrays, MRAs)[5]和最小空洞阵(minimum hole arrays, MHAs)[11],这两种阵列给出了稀疏线阵连续自由度和非连续自由度的上限,但它们都利用搜索而非解析方式确定阵元位置,并不利于实际工程应用。近年来,随着嵌套阵(nested arrays, NAs)[6]和互质阵(coprime arrays, CAs)[7]这两种经典稀疏线阵的提出,众多改进阵型及适用于稀疏线阵的DOA估计算法相继出现[12-19],稀疏线阵相关领域逐渐成为一个新兴的研究热点。具体地,嵌套阵由疏密2级ULA子阵嵌套组成,而互质阵由2个阵元间距大于半波长的均匀子阵叠加组成,与MRA和MHA相比,嵌套阵和互质阵的阵元位置与自由度具有闭合的表达式,便于实际应用且有较好的扩展性。文献[12]扩展互质阵中一个ULA子阵从而获得更长的中央连续段差分共阵,文献[13]将互质结构推广至压缩(compressed)和分置(displaced)2种方式,进一步提高了阵列的自由度。文献[14]在保持嵌套阵中央连续段差分共阵长度前提下降低了阵列互耦。此外,增广嵌套阵[15]、补充互质阵[16]、最大间距约束阵[17]等新型阵列在提高自由度和降低耦合方面也给出了良好的表现。然而,这些稀疏阵的设计很少考虑阵列几何结构的鲁棒性,往往以降低虚拟阵元的冗余性为代价来获取更大的阵列自由度,一旦物理阵元出现随机故障,其差分共阵的中央连续段很可能急剧缩短,实际可用自由度也大打折扣。至于DOA估计算法,几乎所有稀疏线阵都可以使用基于差分共阵的虚拟化阵元类方法,如文献[12]通过对阵列协方差矩阵进行矢量化操作得到超过物理阵元数的虚拟最小间距均匀线阵,利用空间平滑增秩,再使用多重信号分类(multiple signal classification, MUSIC)算法实现波达方向估计。文献[18]提出将阵列协方差按照与虚拟阵元对应关系重排为Toeplitz矩阵,再利用MUSIC算法求解空间谱。文献[19]将压缩感知技术引入DOA估计,对阵列协方差矢量化后,通过lasso回归方法求解由虚拟阵元构成稀疏字典上的展开系数来估计信源方向。文献[20]还提出对差分共阵插值后再进行DOA估计。上述方法中,基于压缩感知和插值的几种方法在理论上可应用于具有非连续自由度的虚拟阵列,但这些方法计算成本高昂,且实际有效工作条件仍有待探索[21];而Toeplitz-MUSIC算法与空间平滑MUSIC算法适用于中央连续段差分共阵,这两种方法计算复杂度相对较低且性能相近,其中空间平滑MUSIC算法在稀疏阵列鲁棒性研究中应用较为普遍[10, 22],因此,本文后续分析及仿真主要基于空间平滑MUSIC方法展开。
关于阵元故障条件下阵列结构鲁棒性的早期研究,侧重从阵列流形[23]和波束模式[24]的角度进行分析,近年来,该领域研究更关注故障传感器对差分共阵的影响,文献[21]分别定义k必要性和k脆弱性,给出了反映差分共阵鲁棒性的量化指标。若移除含k阵元的某子阵会改变原阵列的差分共阵,则称该子阵是k必要的;脆弱性定义为k必要子阵数与所有k阵元子阵数之比,衡量由k个阵元故障引起差分共阵改变的可能性,若k脆弱性较大,传感器随机故障更可能使差分共阵受损,于是阵列鲁棒性较低。但这些概念是基于整个差分共阵的,并不完全适用于其中央连续段。文献[9]对k必要性和k脆弱性理论进行扩展,提出更通用具体的子阵列的重要性函数,为阵列设计与实现成本提供了参考,在此基础上,结合k脆弱性给出了广义k脆弱性的阵列几何鲁棒性框架,该框架可扩展到描述中央连续段差分共阵的鲁棒性,进而可分析空间平滑MUSIC方法的适用性。文献[10]指出冗余对于阵列鲁棒性至关重要,并提出了具有更高鲁棒性的β重冗余阵,但该阵稀疏性并不理想。
对于稀疏线阵,自由度(degree of freedom, DOF)[14]可衡量阵列获取信息的效率,而冗余度(redundancy)[15]则体现阵列获取信息的可靠性。显然,自由度和冗余度是影响故障条件下阵列DOA估计效果的2个主要因素。传统的最小间距均匀线阵采取最密集的方式配置物理阵元,因此具有最高的冗余度和最低的脆弱性,然而由于无法通过虚拟阵元方式扩展自由度,这种阵列可估计的信源十分有限。而其他稀疏阵列牺牲冗余以换取高自由度的特性使阵元故障时中央连续段长度锐减,阵列的鲁棒性较差。此外,现有β重冗余阵列[10]大部分相邻阵元间距为载波半波长,阵元耦合时阵列性能衰减严重,阵列稀疏性有待提升。综上所述,本文采取更加平衡的设计策略,同步优化阵列的冗余性、自由度与稀疏性,提出一种由三段均匀线阵组成的三元冗余阵,并在数学证明的基础上给出其自由度和阵元位置的闭式表达。三元冗余阵的原始差分共阵连续无孔且除最外侧4个虚拟阵元外权重均不小于3,阵列鲁棒性较高。仿真实验表明,与相同阵元数的互质阵、嵌套阵等稀疏线阵相比,在阵元发生随机故障时,本文提出的三元冗余阵能保持更稳定的中央连续段差分共阵,DOA估计性能优势明显。当考虑阵列耦合时,三元冗余阵估计精度优于β重冗余阵。
1 稀疏阵列信号模型设有M个远场窄带非相关信号入射到由N个阵元构成的非均匀线阵上, 阵元位置为vid, vi∈Z, d=λ/2, λ为信号波长, 阵元位置关于半波长的归一化值为S={vi: vi∈Z, i=1, 2, …, N}, 信源入射角度分别为[θ1, θ2, …, θM], 则在t时刻, 阵列接收信号模型为
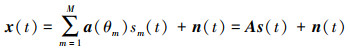
|
(1) |
式中: A=[a(θ1), …, a(θM)]为阵列流形矩阵; a(θm)=[e-j2πv1dsinθm/λ, …, e-j2πvNdsinθm/λ]T为导向矢量; s(t)=[s1(t), s2(t), …, sM(t)]T表示信号波形向量; n(t)为均值为零的高斯白噪声。
由x(t)计算阵列的协方差矩阵为
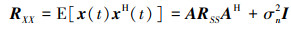
|
(2) |
式中, RSS=E[s(t)sH(t)]=diag([σ12, …, σM2])为信源的协方差矩阵; σn2为噪声功率。
对协方差矩阵RXX矢量化后可得
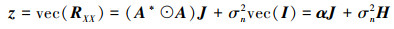
|
(3) |
式中, α=[a*(θ1)⊗a(θ1), …, a*(θM)⊗a(θM)]; J=[σ12, σ22, …, σM2]T; H=vec(I)。
(3) 式与(1)式具有相同的数学模型结构, 因此可以将向量化后的数据z看成是虚拟阵列接收的信号, α相当于方向矩阵, J可看作入射信号矢量, 由此得到的稀疏阵列虚拟阵元位置对应于原始物理阵列中的阵元位置差。
2 阵列鲁棒性相关概念 2.1 虚拟化阵元相关概念对线阵中物理阵元的位置进行自差和互差计算后可将阵列转化至虚拟域, 得到差分共阵, 数学化表述由定义1给出, 差分共阵中从初始阵元起的最长连续子阵称为中央连续段, 数学化表述由定义2给出, 若差分共阵的虚拟阵元自始至终未有间断, 则该差分共阵连续无孔。
定义1 阵元数为N、位置集合为S={vi: vi∈Z, i=1, 2, …, N}的稀疏线阵, 对集合S中元素求差并去除重复值得到差分共阵, 表示为
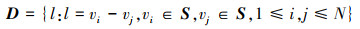
|
(4) |
集合D中含有虚拟阵元的个数称为自由度, 表示为|D|。
定义2 在差分共阵中, 包含0差值虚拟阵元的最长均匀连续子阵称为该差分共阵的中央连续段, 表示为
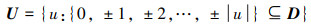
|
(5) |
且U中虚拟阵元数目称为连续自由度(uniform DOF, UDOF), 即UDOF=|U|, 式中, |·|表示集合的势。
定义3 对于任意一个包含在差分共阵D中的位置为l的虚拟阵元定义权重为
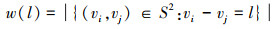
|
(6) |
式中, l∈D, |·|表示集合的势。
定义4 假设阵元故障率独立同分布, 特定故障率下的阵列连续自由度UDOF可看作一个随机变量, 将该随机变量的期望称为平均连续自由度, 定义为

|
(7) |
式中:W为蒙特卡罗实验次数; UDOF, w为第w次实验中阵列的连续自由度数目。
对于接收电磁波信号的线性阵列, 物理阵元间存在相互作用即电磁耦合, 下述定义给出线阵电磁互耦的量化标准。
定义5 互耦率[14]为
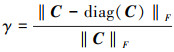
|
(8) |
式中, ||·||F表示矩阵的Frobenius范数运算; diag(·)为矩阵的主对角线元素; C为互耦矩阵, 且近似为B带对称的Toeplitz矩阵[14], C矩阵可写为
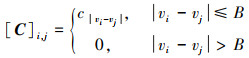
|
(9) |
且1=c0>|c1|>|c2|>…>|cB|>|cB+1|=0。
2.2 阵列鲁棒性评价标准定义6 阵列S上所有大小为k的子阵族为Sk={Y⊆S: |Y|=k}, 当子阵列Y从整个阵列S中删除时差分共阵改变, 则称子阵列Y是k必要的。
定义7 k必要性对应的重要性函数定义为
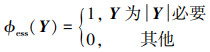
|
(10) |
式中, Y⊆S。
与差分共阵中央连续段U的大小相关的重要性函数定义为
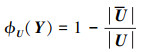
|
(11) |
式中, S=S\Y; U为S的差分共阵的中央连续段。
定义8 广义k脆弱性定义为所有k元子阵的重要性函数之和与k子阵族大小之比
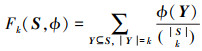
|
(12) |
式中, k=0, 1, …, |S|。广义k脆弱性有Fk(S, ϕess)和Fk(S, ϕU)2种, 范围均为[0, 1]。并且k=1, …, |S|时, Fk(S, ϕess)等价于k脆弱性[21]。后文脆弱性均按此定义。
3 三元冗余阵结构模型 3.1 三元冗余阵结构设计规则三元冗余阵由3个均匀线阵以特定的间隔组合而成, 要求阵元总数N>14。假设参考阵元位于坐标轴原点处, L为相邻阵元归一化间距有序集合, 由L可确定阵元位置。阵列几何结构如图 1所示, d为单位阵元间距, 通常取d=λ/2。阵列结构参数由(13)式给出。

|
| 图 1 三元冗余阵结构配置 |
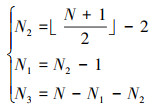
|
(13) |
传感器归一化间距有序集合L定义为
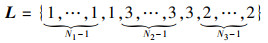
|
(14) |
三元冗余阵的归一化阵元位置有序集合S为
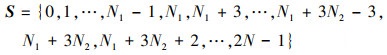
|
(15) |
性质1 由N阵元构成的三元冗余阵, 其差分共阵连续无孔, 自由度为4N-1。
证明 显然差分共阵D关于0对称, 令D+为D中大于等于0的部分, 结合(15)式, 三元冗余阵的阵元最大正间距为

|
(16) |
令G={0, 1, 2, 3, …, 2N-1}, 则只需证明D+=G。
将集合G分为3个子集G1={0, 1, 2, …, N1}, G2={N1+1, N1+2, …, N1+3N2}, G3={N1+3N2+1, N1+3N2+2, …, 2N-1}。
将物理阵列位置集合S分为3个子集S1={0, 1, 2, …, N1}, S2={N1+3, N1+6, …, N1+3N2}, S3={N1+3N2+2, N1+3N2+4, …, 2N-1}。
情形1 证明G1⊆D+。{0, S1}⊆S, 将集合S1与数字0做差集运算, 可得G1⊆D+。
情形2 证明G2⊆D+。{0, 1, 2, S2}⊆S, 将集合S2分别与数字0, 1, 2做差集运算得到3个集合, 这3个集合求并集可得G2⊆D+。
情形3 证明G3⊆D+。{0, 1, S3}⊆S, 将集合S3分别与数字0, 1做差集运算得到2个集合, 将这2个集合求并集, 可得G3⊆D+。并且有G=G1∪G2∪G3=D+, 故该阵列的差分共阵是连续无孔的。D={-(2N-1), …, -2, -1, 0, 1, 2, …, (2N-1)}, UDOF=4N-1。
证毕
性质2 对于三元冗余阵的差分共阵, 除左右最外侧各4个虚拟阵元权重小于3外, 其余虚拟阵元位置的权重均大于等于3。
证明 η=0, 1, …, 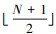
ξ=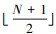
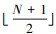
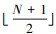
ψ=2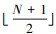
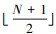
令S(α)∈S, α=0, 1, 2, …, N-1, 当N>14且为偶数时, 有N1≥5, N2≥6, N3=5。
定义可产生差分共阵中虚拟阵元的物理阵元对表示为
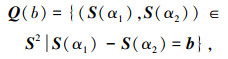
|
(17) |
b∈[1, S(N-1)], ∀α1, α2⊆α且α1>α2
定义产生差分共阵中虚拟阵元的物理阵元对的数目为
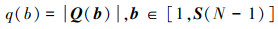
|
(18) |
将D={0, 1, 2, …, S(N-1)}分为4个子集
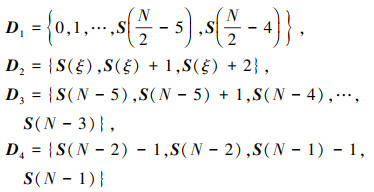
|
分别求出可产生上述子集中虚拟阵元的物理阵元对, 可得b∈D1, D2, D3时, 满足q(b)≥3, b∈D4时满足q(b) < 3。
当N为奇数时, 与N为偶数时同理。
证毕
4 阵列特性分析在本节中将本文提出的三元冗余阵与均匀线阵、扩展互质阵[12]、补充互质阵[16]、最大间距约束阵[17]、嵌套阵[6]、二阶超级嵌套阵[14]等稀疏阵列针对几个鲁棒性关键指标进行对比分析。
4.1 冗余性分析图 2为物理阵元数为17时7种不同阵列的物理阵元配置及其差分共阵中虚拟阵元对应的权重[15]示意图, 由于差分共阵关于参考阵元对称, 故仅考虑正半部分。
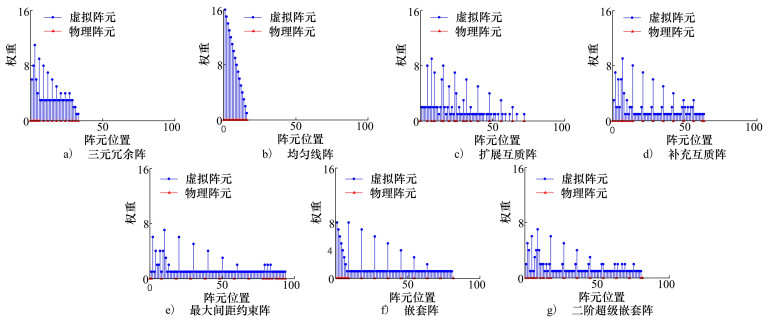
|
| 图 2 阵元位置及差分共阵权重 |
由图 2可知, 尽管图 2b)所示均匀线阵具有最丰富的冗余, 然而均匀线阵无法提供大于物理阵元数的差分共阵; 图 2c)~2g)所示5种稀疏阵列的差分共阵都相对较长, 但其中许多虚拟阵元的权重仅为1, 阵列冗余不足, 显得较为单薄; 相对于另外6种阵列, 图 2a)所示三元冗余阵同时兼顾了冗余性和自由度, 一方面获得了超出物理阵元数的差分共阵, 另一方面阵列冗余也表现出一定厚度, 只有最外侧4个阵元对应冗余小于3, 其他位置冗余数均不小于3。
可靠性是分析阵列冗余性的另一指标。文献[16]定义阵列可靠性为差分共阵中权重大于1的虚拟阵元数与差分共阵中所含不同虚拟阵元总数即相异值之比。当阵元总数从15变化到75时, 各阵型可靠性曲线如图 3所示。
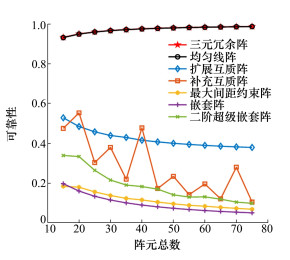
|
| 图 3 可靠性随阵元总数变化 |
由图 3知, 三元冗余阵的可靠性与均匀线阵相近, 始终明显超越其余5种稀疏阵型, 即表明三元冗余阵的冗余虚拟阵元在其差分共阵中的占比远高于其他5种稀疏阵型。
4.2 阵元故障下的自由度分析阵元独立故障率p既是时间t的函数, 也是平均失效率λ的函数, 文献[25]将其建模为p=1-e-λt。若平均失效率λ=0.000 01, 即阵元平均100 000 h发生一次故障, 则一年后阵元故障率p=0.083 9。在阵元随机故障条件下, 在差分共阵中央连续段长度具有随机性, 其平均值可以反映阵列自由度的整体水平。取物理阵元数为17时比较各种阵列配置在不同故障率下的平均连续自由度, 进行20 000次蒙特卡罗实验, 仿真结果如图 4所示。
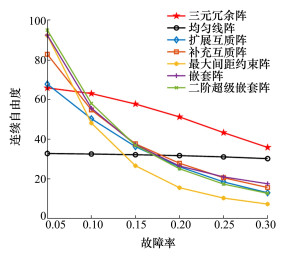
|
| 图 4 连续自由度随故障率变化 |
由图 4可知, 随着故障率增大, 6种稀疏阵列的中央连续段平均长度都呈现递减趋势, 而当随机故障率不超过0.3时, 均匀线阵由于具备高度冗余, 其连续自由度未出现明显降低。当随机故障率处于0.08~0.3之间时, 红线所示三元冗余阵具有最高的连续自由度, 这是由于三元冗余阵的设计兼顾了自由度和冗余性, 在阵元随机故障条件下, 其差分共阵仍能保持较长的中央连续段, 而其余稀疏阵和均匀线阵仅优化了单一指标未能在自由度和冗余性之间取得平衡。稀疏阵往往牺牲冗余实现高自由度, 当必要阵元出现故障时将破坏差分共阵的连续性, 导致连续自由度急剧减少; 而均匀线阵尽管冗余度最高, 连续自由度减少程度缓慢, 但由于其自由度不超过物理阵元数, 阵列连续自由度的上限不高。
4.3 阵列几何结构的鲁棒性分析针对阵元故障对整个差分共阵D和差分共阵中央连续段U的影响, 比较各阵型的阵元重要性。图 5a)~5g)分别为三元冗余阵、均匀线阵、扩展互质阵、补充互质阵、最大间距约束阵、嵌套阵和二阶超级嵌套阵的物理阵元重要性分布示意图。
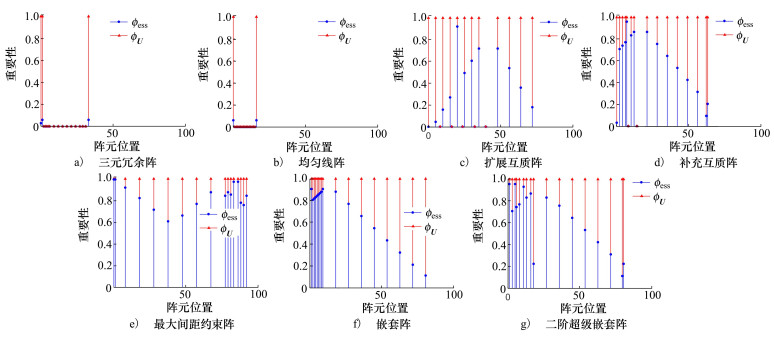
|
| 图 5 不同阵列的阵元重要性 |
由图 5可知, 无论是基于k必要性还是差分共阵的中央连续段, 三元冗余阵中阵元的重要性略高于均匀线阵, 但三元冗余阵中大部分阵元的重要性明显低于其余5种稀疏阵列, 即多数阵元相对不重要, 不同阵元故障改变差分共阵的程度较低, 从而提高了阵列的鲁棒性, 而其余稀疏线阵大部分阵元明显具有较高的重要性, 不同阵元的故障会极大程度改变差分共阵, 阵列的鲁棒性较弱。
下面比较不同阵型分别基于U和基于k必要性的广义k脆弱性, 结果如图 6所示。
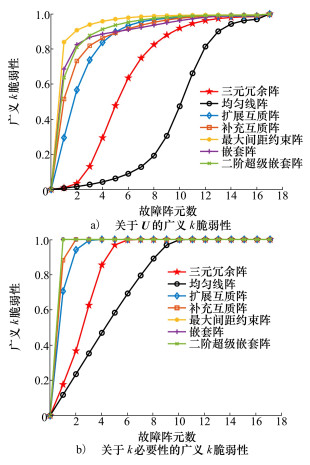
|
| 图 6 不同阵列的广义k脆弱性 |
由图 6可知, 随着故障阵元个数增加, 各阵型的广义k脆弱性均逐渐增加。相对于差分共阵的中央连续段U, 相同数目的故障阵元更易改变整个差分共阵D, 关于k必要性的广义k脆弱性更容易达到1。在故障阵元个数一定范围内, 本文提出的三元冗余阵的广义k脆弱性相对于其余5种稀疏阵列更小, 仅大于均匀线阵的广义k脆弱性, 即三元冗余阵的广义k脆弱性处于均匀线阵和其余稀疏线阵之间, 从阵列的几何结构来说具有较好的鲁棒性。
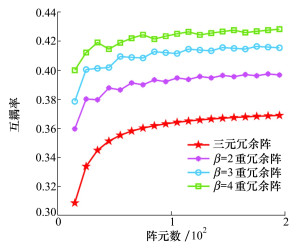
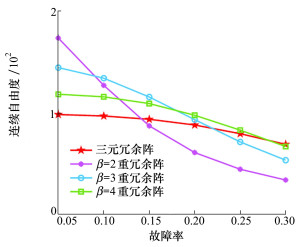
4.4 与β重冗余阵的对比分析β重冗余阵(β=2, 3, 4)[10]的差分共阵权重较为平坦, 参数β指除最外侧β-1个虚拟阵元外权重的最小值, β与自由度呈反比。由性质2可知, 除了最外侧阵元, 三重冗余阵虚拟阵元权重都不小于3, 其总体冗余性能高于β=3重冗余阵。图 7为不同阵元数下三元冗余阵、β重冗余阵(β=2, 3, 4)的互耦率, 图 8为25个物理阵元时三元冗余阵与β重冗余阵(β=2, 3, 4)在不同故障率下的平均连续自由度对比图。由图 7知, 由于三元冗余阵相比β重冗余阵更加稀疏, 因此具有最小的互耦率。由图 8可看出, 阵元故障率较低时, 三元冗余阵平均连续自由度不及β重冗余阵, 但故障率超过0.25后, 其连续自由度逐渐超越β重冗余阵。
|
| 图 7 互耦率随阵元数变化情况 |
|
| 图 8 连续自由度随故障率变化情况 |
本节针对前文所述阵列, 利用空间平滑MUSIC算法进行信源DOA估计, 比较各阵列的均方根误差(root mean square error, RMSE), 进行实验时同文献[22], 只考虑该方法有效的实例。实验中阵列DOA估计的均方根误差定义为
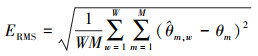
|
(19) |
式中:W为蒙特卡罗实验次数; M为信源数; θm是第m个信源的真实入射方向; 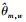
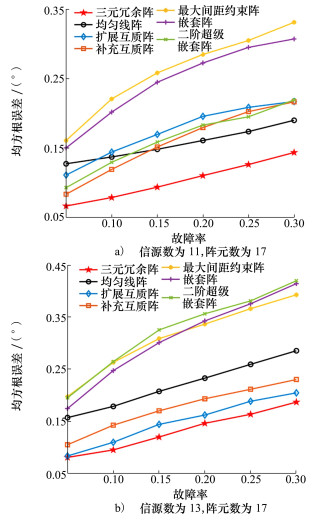
实验1 不同故障率时阵列均方误差对比。针对阵元数为17的7种阵列, 由图 4知, 当故障率大于0.25时, 许多对比阵型连续自由度低于15, 信源数过大时无法估计DOA, 故选择均能实现DOA估计的信源数来进行仿真。设信噪比为5 dB, 快拍数为3 000, 进行20 000次蒙特卡罗实验, 设有11个或13个均匀分布在[-60°, 60°]内的信源入射, 对各阵型进行DOA估计得到的RMSE曲线如图 9所示。
|
| 图 9 均方根误差随故障率变化情况 |
如图 9所示,在0.05~0.3的整个故障率区间内,所有阵列的均方根误差与故障率都呈正相关,而本文提出的三元冗余阵始终表现最优。当故障率高于0.08时,回顾图 4可知,三元冗余阵由于同时优化了自由度和冗余性,本就具有高于其他阵列的平均连续自由度,因而其在利用空间平滑MUSIC算法进行DOA估计后具有最低的均方根误差并不令人意外。而当故障率低于0.08时,三元冗余阵的均方根误差仍然低于其余对比阵列,这一结果似乎与图 4中平均自由度的排序相矛盾。实际上,图 5显示出三元冗余阵除首尾外大部分阵元的重要性都不高,不同物理阵元出现故障对差分共阵造成影响的差异并不大。而其余稀疏阵,虽然故障后的平均自由度较高,但阵列中含有不少较为“致命”的高重要性阵元,不同物理阵元出现故障对差分共阵造成的影响参差多样,差分共阵结构不稳定。如果把特定故障率下连续自由度看作一个随机变量,三元冗余阵连续自由度的方差较小因而也更稳定集中,罕有特别低的连续自由度出现,而其余稀疏阵的连续自由度方差较大因而取值分散,其中一些自由度很低的阵列会产生非常大的估计误差,最终导致平均均方根误差大于三元冗余阵。
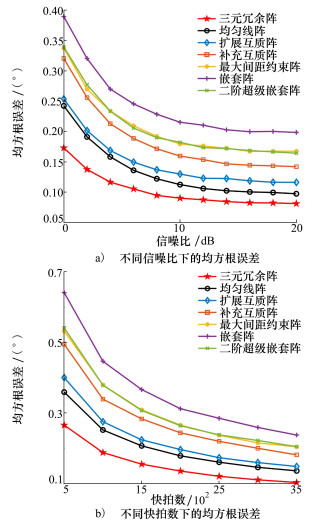
实验2 不同信噪比及快拍数时阵列均方误差对比。取阵元总数为17,故障率为20%,有10个远场信号从[-60°, 60°]入射,快拍数为3 000,信噪比从0 dB增加到20 dB,蒙特卡罗实验次数为20 000,RMSE变化曲线如图 10a)所示。其他参数不变,设信噪比为5 dB,快拍数从500增加到3 500, 均方根误差曲线如图 10b)所示。
|
| 图 10 均方根误差曲线 |
由图 10可知,故障率为20%时,随着信噪比和快拍数的增大,各阵列的DOA估计性能均有所提高。其中三元冗余阵的估计误差最小,相比于均匀线阵和其他稀疏线阵,具有最高的估计精度,这是由于三元冗余阵具有更稳定的差分共阵和更多的连续自由度,最终使得三元冗余阵的估计效果最好。
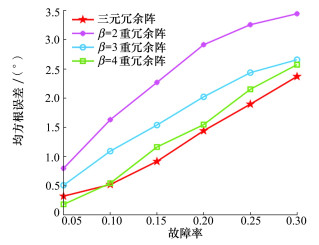
实验3 阵列耦合条件下均方误差对比。经大量仿真发现,尽管几种典型稀疏阵阵元间距较大而具有较小的互耦率,但在随机故障发生后,稀疏阵的连续自由度取值极为分散,方差较大,其中自由度较低的一部分阵列加之耦合影响,可估信源数会出现锐减。可以说对于稀疏阵,耦合加剧了阵列的脆弱性,容易导致DOA估计失效。而三元冗余阵与β重冗余阵尽管互耦率较大,但由于冗余度也较高,随机故障时发生非常低自由度情况的概率很小。因此,耦合因素对冗余阵的影响不如稀疏阵那样强烈,考虑耦合时,2类冗余阵仍能保持相对稳定的DOA估计能力。基于上述原因,耦合条件下阵列性能对比分析主要集中于所提三元冗余阵与已有鲁棒性β重冗余阵。阵列耦合时,三元冗余阵与β重冗余阵(β=2, 3, 4)在不同故障率下的RMSE性能如图 11所示。图 11对应场景中阵元总数为25,有7个信源。
|
| 图 11 均方根误差随故障率变化 |
由图 11可知,在故障率高于0.11时,三元冗余阵具有最低的均方误差。一方面原因在于三元冗余阵具有比β重冗余阵更低的阵列耦合,如图 7所示;另一方面,随着故障率的增大,三元冗余阵逐渐趋近β重冗余阵的连续自由度并略有胜出,如图 8所示。两因素叠加,使所提阵列表现出更好的估计性能。
6 结论针对阵元随机故障,平衡考虑阵列自由度、冗余性、阵列耦合等多个角度,提出一种具备高鲁棒性,低互耦率的三元冗余稀疏线阵。对比分析及仿真实验显示,阵元随机故障时,三元冗余阵DOA估计性能优于典型稀疏阵,是一种有效的鲁棒阵列结构;耦合条件下,三元冗余阵具有比现有β重冗余阵更高的DOA估计精度;同时,在获得相近性能时,三元冗余阵的孔径比β重冗余阵要小,因而在空间受限的环境与平台中更具优势。任意多于14的物理阵元,都可按照明确的解析规则构造三元冗余阵并计算其差分共阵自由度;数学证明三元冗余阵的差分共阵具有2条性质:①连续无孔;②除最远端4个虚拟阵元外权重均不小于3。构造了平均连续自由度指标,该指标能够反映自由度与冗余性2个关键因素对稀疏阵性能的综合影响,仿真实验验证了这一指标的有效性与合理性。为获得更大平均连续自由度,应使阵列的差分共阵权重从中央原点往两侧递减,当给定物理阵元数和随机故障率后,如何设计阵列结构获得最大平均连续自由度,是一个有趣的问题,也为后续的鲁棒阵列设计研究提供了方向与借鉴。
| [1] | WAN L T, HAN G J, SHU L, et al. The application of DOA estimation approach in patient tracking systems with high patient density[J]. IEEE Trans on Industrial Informatics, 2016, 12(6): 2353-2364. DOI:10.1109/TII.2016.2569416 |
| [2] | SHAIKH A H, DANG X Y, HUANG D Q. New generalized multi-structured MIMO radar configuration with increased degrees of freedom[J]. IEEE Communications Letters, 2021, 25(4): 1293-1297. DOI:10.1109/LCOMM.2021.3049855 |
| [3] |
樊宽, 孙超, 刘雄厚, 等. 联合匹配滤波MIMO声呐发射分集平滑DOA估计方法[J]. 西北工业大学学报, 2020, 38(1): 6-13.
FAN Kuan, SUN Chao, LIU Xionghou, et al. MIMO sonar DOA estimation with joint matched-filtering based on transmission diversity smoothing[J]. Journal of Northwestern Polytechnical University, 2020, 38(1): 6-13. (in Chinese) DOI:10.3969/j.issn.1000-2758.2020.01.002 |
| [4] | PATWARI A. Sparse linear antenna arrays: a review[EB/OL]. (2021-09-02)[2022-05-04]. https://www.intechopen.com/chapters/78401 |
| [5] | MOFFET A T. Minimum-redundancy linear arrays[J]. IEEE Trans on Antennas and Propagation, 1968, 16(2): 172-175. DOI:10.1109/TAP.1968.1139138 |
| [6] | PAL P, VAIDYANATHAN P P. Nested arrays: a novel approach to array processing with enhanced degrees of freedom[J]. IEEE Trans on Signal Processing, 2010, 58(8): 4167-4181. DOI:10.1109/TSP.2010.2049264 |
| [7] | VAIDYANATHAN P P, PAL P. Sparse sensing with co-prime samplers and arrays[J]. IEEE Trans on Signal Processing, 2011, 59(2): 573-586. DOI:10.1109/TSP.2010.2089682 |
| [8] | WANG M Z, NEHORAI A. Coarrays, MUSIC, and the Cramér-Rao bound[J]. IEEE Trans on Signal Processing, 2016, 65(4): 933-946. |
| [9] | LIU C L. A general framework for the robustness of structured difference coarrays to element failures[C]//IEEE 11th Sensor Array and Multichannel Signal Processing Workshop, 2020: 1-5 |
| [10] | ZHU D, WANG S Y, LI G. Multiple-fold redundancy arrays with robust difference coarrays: fundamental and analytical design method[J]. IEEE Trans on Antennas and Propagation, 2021, 69(9): 5570-5584. DOI:10.1109/TAP.2021.3083819 |
| [11] | VERTATSCHITSCH E, HAYKIN S. Nonredundant arrays[J]. Proceedings of the IEEE, 1986, 74(1): 217. |
| [12] | PAL P, VAIDYANATHAN P P. Coprime sampling and the MUSIC algorithm[C]//Digital Signal Processing and Signal Processing Education Meeting, 2011: 289-294 |
| [13] | QIN S, ZHANG Y D, AMIN M G. Generalized coprime array configurations for direction-of-arrival estimation[J]. IEEE Trans on Signal Processing, 2015, 63(6): 1377-1390. DOI:10.1109/TSP.2015.2393838 |
| [14] | LIU C L, VAIDYANATHAN P P. Super nested arrays: linear sparse arrays with reduced mutual coupling-part Ⅰ: fundamentals[J]. IEEE Trans on Signal Processing, 2016, 64(15): 3997-4012. DOI:10.1109/TSP.2016.2558159 |
| [15] | LIU J Y, ZHANG Y M, LU Y L, et al. Augmented nested arrays with enhanced DOF and reduced mutual coupling[J]. IEEE Trans on Signal Processing, 2017, 65(21): 5549-5563. DOI:10.1109/TSP.2017.2736493 |
| [16] | WANG X M, WANG X. Hole identification and filling in k-times extended co-prime arrays for highly-efficient DOA estimation[J]. IEEE Trans on Signal Processing, 2019, 67(10): 2693-2706. DOI:10.1109/TSP.2019.2899292 |
| [17] | ZHENG Z, WANG W Q, KONG Y Y, et al. MISC array: a new sparse array design achieving increased degrees of freedom and reduced mutual coupling effect[J]. IEEE Trans on Signal Processing, 2019, 67(7): 1728-1741. DOI:10.1109/TSP.2019.2897954 |
| [18] | LIU C L, VAIDYANATHAN P P. Remarks on the spatial smoothing step in coarray MUSIC[J]. IEEE Signal Processing Letters, 2015, 22(9): 1438-1442. DOI:10.1109/LSP.2015.2409153 |
| [19] | ZHANG Y D, AMIN M G, HIMED B. Sparsity-based DOA estimation using co-prime arrays[C]//2013 IEEE International Conference on Acoustics, Speech and Signal Processing, 2013: 3967-3971 |
| [20] | ZHOU C W, GU Y J, FAN X, et al. Direction-of-arrival estimation for coprime array via virtual array interpolation[J]. IEEE Trans on Signal Processing, 2018, 66(22): 5956-5971. DOI:10.1109/TSP.2018.2872012 |
| [21] | LIU C L, VAIDYANATHAN P P. Robustness of difference coarrays of sparse arrays to sensor failures-part Ⅰ: a theory motivated by coarray MUSIC[J]. IEEE Trans on Signal Processing, 2019, 67(12): 3213-3226. DOI:10.1109/TSP.2019.2912882 |
| [22] | LIU C L, VAIDYANATHAN P P. Robustness of difference coarrays of sparse arrays to sensor failures-part Ⅱ: array geometries[J]. IEEE Trans on Signal Processing, 2019, 67(12): 3227-3242. DOI:10.1109/TSP.2019.2912877 |
| [23] | ALEXIOU A, MANIKAS A. Investigation of array robustness to sensor failure[J]. Journal of the Franklin Institute, 2005, 342(3): 255-272. DOI:10.1016/j.jfranklin.2004.11.005 |
| [24] | CARLIN M, OLIVERI G, MASSA A. On the robustness to element failures of linear ADS-thinned arrays[J]. IEEE Trans on Antennas and Propagation, 2011, 59(12): 4849-4853. DOI:10.1109/TAP.2011.2165510 |
| [25] | O'CONNOR P, KLEYNER A. Practical reliability engineering[M]. New York: John Wiley & Sons, 2012. |




