由于实际工程中存在着大量的不确定性[1], 基于可靠性的结构设计已成为一种有效的分析处理手段。在灵敏度分析[2]、非概率可靠性[3]或基于可靠性的设计优化(RBDO)[4]等众多领域中, 失效概率与设计参数的函数关系, 被称为失效概率函数(FPF), 是其关键及难点问题之一。当得到参数的失效概率函数时, 对其求导即可以很容易地得到灵敏度; 在非概率可靠性分析中, 可以由失效概率函数得到失效概率的最小值和最大值结果; 在可靠性设计优化中, 代入失效概率函数, 可以将目标可靠性优化问题解耦为一个等价的确定性优化问题, 该方法被称为解耦方法。
在实际应用中, 因通常需要在不同的设计参数值下进行多次的可靠性分析,要想得到与设计参数相关的失效概率函数面临很大的挑战。目前可靠性分析已研究出许多方法, 其中包括近似分析方法, 如一阶/二阶可靠度法——FORM/SORM[5]。这类方法通常是非常有效的, 但是在处理非线性极限状态函数时, 尤其是在考虑非渐近问题时, 这类方法可能会存在精度问题。另一类方法是基于模拟的方法, 如蒙特卡罗模拟[6]、重要抽样[7]、子集模拟[8]和线抽样[9]等, 这类方法通常计算效率非常低。在实际工程问题中特别是涉及大型有限元模型时, 这类方法的可行性较低。因此, 大量的可靠性分析计算使得直接估计失效概率函数的计算变得特别困难。
目前失效概率函数的估计方法大致可分为三类。第一类为代理模型方法, 实验设计是该方法的关键。实验设计是通过在设计参数空间中选择一些预定义的插值点, 应用各种代理模型来构建近似值, 然后对设计参数的插值网格点进行可靠性分析, 确定代理模型的系数。例如, Gasser等[10]对设计参数采用预定义的二次多项式函数来近似失效概率函数的对数; 而Jensen[11]采用线性多项式函数逼近失效概率函数的对数。其他类型的替代模型方法, 如Kriging方法[12]、支持向量机[13]等在可靠性分析中被广泛应用于逼近极限状态函数[14], 也可以用来逼近失效概率函数。
第二类方法是通过单次常规可靠性分析的信息来局部逼近失效概率函数, 主要是获得随机变量分布参数的失效概率函数。例如, Zou等[15]基于一次可靠性分析中获得的可靠性灵敏度信息, 采用一阶泰勒级数展开将失效概率函数表示为分布参数的线性函数。Yuan[16]提出了一种加权的抽样方法, 将失效概率函数的估计表示为一次可靠性分析中产生的样本的显式函数形式。此外, Yuan与Song等[17-18]提出基于一次线抽样的信息来求解失效概率函数。需要注意的是, 这些方法主要得到的都是失效概率函数的局部近似。
第三类估计失效概率函数的方法是在扩展空间中进行可靠性问题分析。Au[19]首先提出在扩充空间中利用贝叶斯规则对失效概率函数进行变换, 然后通过单次扩充可靠性分析对失效概率函数进行估计, 但其包含的密度函数估计采用直方图来显示; Ching等[20-21]遵循扩展可靠性思想, 提出采用最大熵方法来估计其中设计参数的后验分布, 从而将失效概率函数显式化; 在扩展空间思想基础上, Yuan等[22]进一步研究了失效概率函数与分布参数的内在关系, 推导出了密度函数的积分式, 使得失效概率函数可通过样本平均来估计, 避免了求解过程中的分布拟合。
本文提出了一种自适应增强线抽样的全局失效概率函数估计方法(AALS)。该方法通过组合一系列的增强线抽样方法的局部失效概率函数来获得全局失效概率估计; 并提出了一种自适应策略在特定参数取值处进行局部失效概率函数估计。所提方法能够克服原有增强线抽样方法的局部性, 且使得失效概率函数的求解能够保证全局上的效率和精度最优。
1 失效概率函数定义在本文提出的方法中, 关于失效概率对设计参数的函数被称为失效概率函数(FPF), 记为PF(θ), θ=[θ1, …, θnθ]是设计参数的向量。当设计参数为结构随机变量x的分布参数(例如均值)时, PF(θ)可表示为
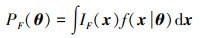
|
(1) |
式中:F={x: g(x) < 0}为失效域, g(·)为极限状态函数; IF(x)为失效域指示函数, 如果x∈F则IF(x)=1, 否则IF(x)=0;f(x|θ)是在分布参数取值为θ的条件下x的条件概率密度函数(PDF)。
2 基于自适应线抽样的失效概率函数求解方法 2.1 失效概率估计的增强线抽样增强线抽样(augmented line sampling, ALS)方法是一种高效的局部估计失效概率函数的方法[23-24]。在本文中, 采用该方法对失效概率函数进行局部估计。在增强线抽样中, 引入辅助抽样密度函数f(x|θ*), 其中θ*是固定的设计参数某一取值, 可将(1)式的失效概率函数PF(θ)改写为

|
(2) |
随后将其转换为标准正态空间。从非正态变量到标准正态变量(用Txu表示)的转换及逆变换(Tux)为
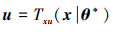
|
(3) |
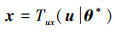
|
(4) |
将(4)式代入(2)式, 进一步可将PF(θ)改写为
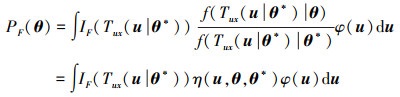
|
(5) |
式中,φ(u)为标准正态分布的概率密度函数。
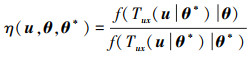
|
(6) |
为2个概率密度函数的比值。公式(5)积分公式可通过线抽样的方法来估计。为此, 引入坐标变换
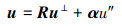
|
(7) |
式中:R是n×(n-1)维旋转矩阵; u⊥是(n-1)×1维向量; α=[α1, α2, …, αn]是单位重要方向向量, 当基本随机变量x分布为f(x|θ*)时确定; u″为标量坐标。基于(7)式, 公式(5)中所示的概率积分可写为
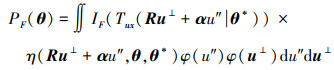
|
(8) |
式中:φ(u″)是一维标准正态分布的概率密度函数; φ(u⊥)是(n-1)维标准正态分布的概率密度函数。
由此可以根据φ(u⊥)分布生成u⊥的样本(记为{u⊥(j): j=1, 2, .., N}), 失效概率函数可以由(9)式计算
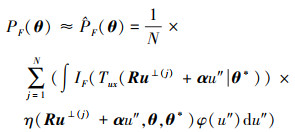
|
(9) |
考虑到
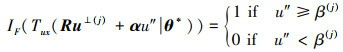
|
(10) |
则失效概率函数估计可写为
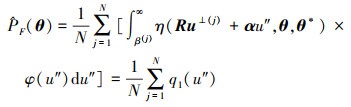
|
(11) |
式中,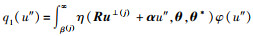
当所有的随机变量都假定为独立正态分布时, 即xi~N(μi, σi2), 同时设计参数仅为变量分布的均值。在这种情况下, xi=Tux(ui|θi*)=uiσi+μi*=uiσi+θi*, 那么在公式(6)中η(u, θ, θ*)可写为
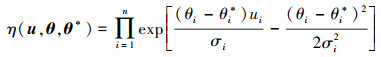
|
(12) |
将(7)式代入(12)式可以得到

|
(13) |
式中

|
(14) |
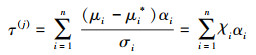
|
(15) |
式中:Ri是矩阵R的第i行; αi是向量α的第i个分量, 且χi=(θi-θi*)/σi。因此, 还有ui(j)=Riu⊥(j)+αiu″(j)。
由公式(13), 一维积分q1(u″)可改写为
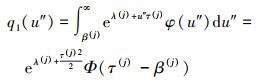
|
(16) |
因此, 公式(11)的失效概率函数估计表达式为
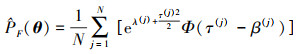
|
(17) |
对应的估计值的方差也可以通过公式(18)得出
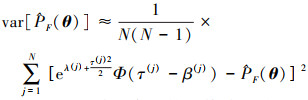
|
(18) |
可以看出, 失效概率函数的估计可转换为一个简单的函数, 该函数由仅使用一次f(x|θ*)完成线抽样所产生的样本来表示。通过这种方法, 避免了多次重复的可靠性分析, 因此通过增强线抽样方法获得了较高的计算效率。增强线抽样的细节可参考文献[14]。
2.2 全局失效概率函数估计的组合算法所提方法的第二个主要步骤是将各个局部失效概率估计
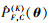
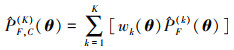
|
(19) |
式中,wk(θ)为第k次(k=1, …, K)迭代的权重函数。为了确保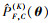
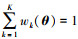

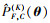
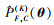
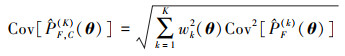
|
(20) |
组合算法的性能很大程度上取决于权重。权重的确定通常有3种方法: ①等权重; ②找到使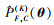
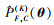
变异系数是估计量的一个重要特征, 亦可根据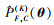

|
(21) |
公式(21)的证明细节见附录A。
2.3 自适应策略所提方法为多次局部估计的融合。在第i次局部失效概率函数估计中, 辅助抽样密度函数f(x|θ*(i))中θ*(i)的选择影响了所提方法的效率, 因此应严谨选择θH(i)。通常, 这些点可以预先通过一定的规则进行选取, 例如通过实验设计方法, 如中心设计法; 或采用随机方法, 如蒙特卡罗模拟(MCS)、拉丁超立方抽样(LHS)等。然而, 这种先验的实验设计可能不是最有效的方法。
为此本文提出了一种自适应策略, 即依据失效概率估计的变异系数来自适应地选择特定的参数取值点来进行局部失效概率估计, 最后运用上述融合方法构建全局失效概率估计。本文提出一种基于确定局部失效概率函数估计量位置的自适应策略。考虑到估计量的统计特性, 变异系数是失效概率函数估计量局部收敛的一个重要且很好的特征, 因此令全局失效概率函数估计量的变异系数作为一个决策依据来确定下一个局部失效概率函数估计量, 进而扩大至全局估计量, 即选择变异系数值最大的设计参数值作为下一个辅助抽样密度函数的支持参数值。
假设当前为第i次迭代, 由(19)式和(20)式计算出对应的全局失效概率函数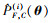
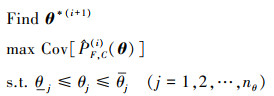
|
(22) |
公式(22)表明, 下一个辅助抽样密度函数的参数值点θ*(i+1)应是全局失效概率函数估计变异系数最大处所对应的点。因此, 基于该辅助参数值点进行局部估计后, 将改善在该区域的全局失效概率函数估计的精度, 从而能有效地提高失效概率函数估计的收敛性。需要指出的是, 求解(22)式优化问题不需要进行任何极限状态函数的计算, 采用任何优化算法都可以较好地求解。
3 算例本节给出2个例子来说明本文所提出方法的优越性。分别采用不同的方法来进行分析和比较: 原有的增强线抽样(ALS)方法、扩展空间的重要抽样法[22](ASI-IS)以及本文所提出的自适应增强线抽样方法(AALS)。此外, 采用直接蒙特卡罗模拟法或重要性抽样法得到失效概率的逐点值, 并将其作为“精确值”。所有算例的停止条件为Ctol=0.2。
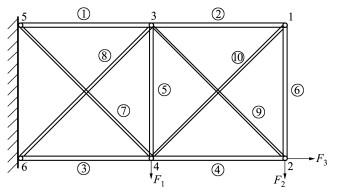
3.1 算例1:十杆算例十杆铝桁架结构如图 1所示。
|
| 图 1 十杆铝桁架 |
桁架受垂直力F1和F2, 水平力F3, 其横向和纵向杆的长度为L, 弹性模量为E。各个杆件的截面积分别为Aj(j=1, 2, …, 10)。考虑结构节点2垂直位移δ2不超过许用位移dy, 极限状态函数定义为
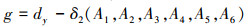
|
(23) |
式中,垂直位移δ2可以表示为
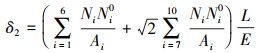
|
(24) |
式中,轴向力Nj(j=1, 2, …, 10)可由平衡方程和变形协调方程得到
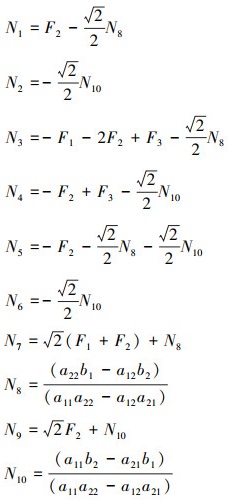
|
(25) |
式中

|
(26) |
Ni0由公式(25)中F1=F3=0和F2=1条件下得到。
各变量的分布信息如表 1所示。其中杆1和杆3的截面积均服从正态分布, 取其均值作为设计参数, 即A1~N(θ1, 1)和A3~N(θ2, 1), 设计域为θ1∈[6, 10]cm和θ2∈[6, 10]cm。
| 变量 | 分布类型 | 均值 | 变异系数 |
| 截面积A1/cm2 | 正态 | θ1∈[6, 10] | 0.1 |
| 截面积A3/cm2 | 正态 | θ2∈[6, 10] | 0.1 |
| 截面积Ai/cm2 | 正态 | 8 | 0.1 |
| 长度L/m | 正态 | 1.5 | 0.1 |
| 弹性模量E/GPa | 正态 | 70 | 0.1 |
| 载荷F1/kN | 正态 | 500 | 0.1 |
| 载荷F2/kN | 正态 | 100 | 0.1 |
| 载荷F3/kN | 正态 | 100 | 0.1 |
采用本文所提出的方法求解该问题的全局失效概率函数。首先设置初始局部估计的参数值为设计区域中部的θ*(1)=[8, 8], 求解相应的设计点, 采用改进一次二阶矩(AFOSM)来进行求解。每个局部失效概率估计采用N=300个样本的增强线抽样来进行求解。
图 2给出了本文方法得到的二维失效概率函数结果, 以及估计量的二维变异系数结果。可以看出, 最终的变异系数值都小于0.2。
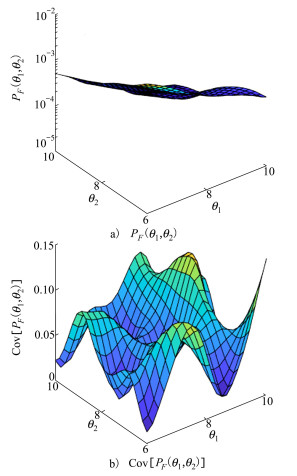
|
| 图 2 所提出方法的二维失效概率函数结果(算例1) |
图 3显示了每次迭代中估计量的变异系数值, 以及由自适应策略确定出的下一次迭代的辅助抽样函数的参数值。可以看到, 辅助参数值点位于变异系数最大的点上(图中红圆点处)。随着迭代的进行, 估计量的变异系数变得越来越小。
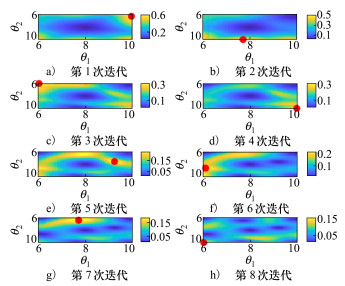
|
| 图 3 每次迭代中失效概率函数的变异系数结果(算例1) |
将本文方法与增强线抽样方法(ALS)和扩展空间重要抽样方法(ASI-IS)方法进行了比较。所有这些方法都是在相同数量的抽样模拟样本数下进行比较, 即NT=N×K=300×8=2 400(K为总迭代次数)。
图 4显示了一维失效概率函数结果以及其变异系数。其中“MCS”表示采用MCS方法得到的视为精确值的结果。从图 4b)中可以看出, ALS失效概率函数在θ2=6附近区域(即θ2∈[6, 7])存在显著误差, 并且θ1和θ2在区间[6, 7]和[9.5, 10]内, 变异系数也明显较大。综合来看, ASI-IS和提出的AALS获得了与直接MCS结果较一致的结果, 而所提出的AALS方法在大部分设计区域拥有相对较小的变异系数, 且变异系数值小于0.2。这说明本文提出的AALS方法比ALS和ASI-IS更加高效。
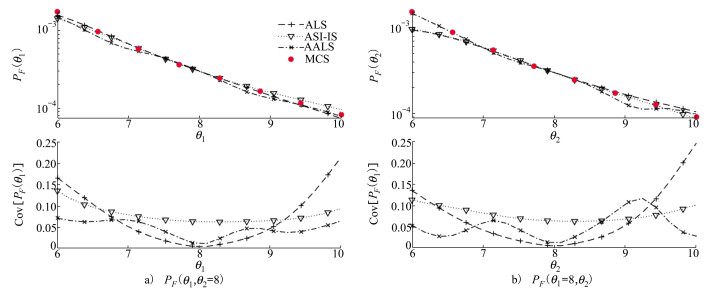
|
| 图 4 不同方法的失效概率函数结果对比(算例1) |
本节对所提AALS方法在不同数量的样本和初始支持参数点设置下的性能进行了研究。该方法采用不同初始辅助参数点值θ*(1), 即: ①初始设计θ*(1)=[6, 6]; ②初始设计θ*(1)=[8, 8]; ③初始设计θ*(1)=[10, 10], 进行多次重复计算。
图 5给出了在不同初始辅助参数点值下采用所提出方法的迭代次数与每次迭代使用的样本数的关系。NT是模拟抽样样本数, 而Nall包括模拟样本和每次迭代求解设计点的计算样本。算例1中, 计算设计点大约需要调用110次极限状态函数。可以看出, 当样本数N增加时, 迭代次数K减少, 但总样本数增加。而不同初始点对方法性能影响不是很大。
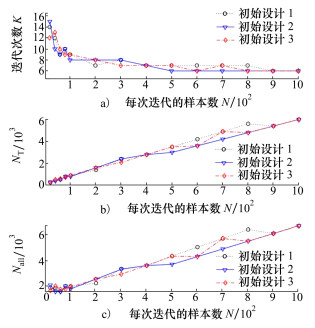
|
| 图 5 不同样本点设置下所提方法的迭代次数与计算代价(算例1) |
结果表明, N的选取影响所提出方法的效率, 应适当选取N。首先, 建议根据停止准则选择N, 例如, 如果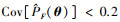
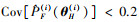
某喷气发动机涡轮叶片结构如图 6所示。
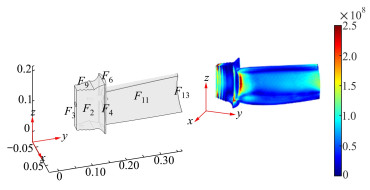
|
| 图 6 涡轮叶片的几何形状和von Mises应力(算例2) |
涡轮径向排列的叶片通常由镍合金制成, 这些合金能抵抗极端高温的气体。在极端高温的条件下, 这种材料会显著膨胀, 产生机械应力和变形。为了避免机械故障和叶片尖端与机匣之间的摩擦, 叶片设计必须考虑机械应力和变形。将破坏定义为结构最大von Mises应力超过给定应力σa=1.5 GPa, 对应的极限状态函数为
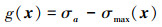
|
(27) |
式中, σmax(x)为热压联合作用下叶片的最大von Mises应力; x=[E, λ, γCTE, p1, p2, Kapp, T1, T2]为基本随机变量向量; E, λ, γCTE和Kapp分别为镍基合金(NIMONIC 90)的弹性模量、泊松比、热膨胀系数和导热系数; p1和p2为叶片压力侧和吸力侧的压力载荷, 压力载荷是由于高压气体围绕在叶片压力侧和吸力侧所产生的; T1为内部冷却空气温度, T2为压力侧和吸力侧温度。假设这些变量都是独立的正态随机变量, 其分布参数如表 2所示。
| 随机变量 | 均值 | 标准差 |
| E/GPa | θ1=μE∈[190, 300] | 23 |
| γCTE/(10-6·K-1) | θ2=μγCTE∈[10, 25] | 1.3 |
| λ | 0.27 | 0.027 |
| p1/kPa | 500 | 50 |
| p2/kPa | 450 | 45 |
| Kapp/(W·m-1·K-1) | 11.5 | 1.15 |
| T1/℃ | 150 | 15 |
| T2/℃ | 1 000 | 100 |
该例子中E和γCTE的平均值(即θ=[μE, μγCTE])被设定为设计变量, 它们的设计域分别为θ1∈[190, 300](GPa)和θ2∈[10, 25](1/K)。
将本文所提出方法应用于求解该问题的全局失效概率函数。首先设置初始辅助参数点值θ*(1)=[245, 17.5], 求解相应的设计点, 取N=100。
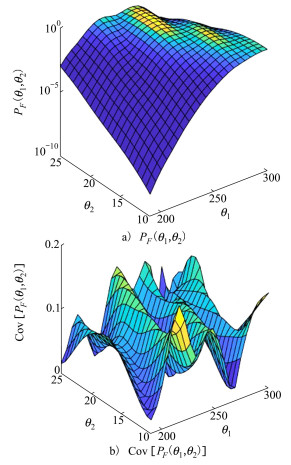
图 7给出了该方法得到的二维失效概率函数结果, 以及估计量的二维变异系数。可以看出, 最终的变异系数值都小于0.2。
|
| 图 7 所提出方法的二维失效概率函数结果(算例2) |
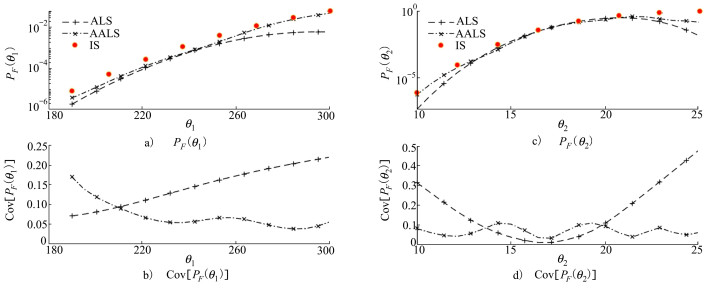
图 8显示了本文所提方法和ALS方法的一维失效概率函数结果以及它们的变异系数, 同时都使用相同的样本总数, 即采用NT=N×K=100×10=1 000个样本。其中‘IS’表示采用重要抽样方法得到视为精确值的结果。从图 8a)~8b)中可以看出, ALS失效概率函数在θ1=280附近区域(即θ1∈[260, 300])存在显著误差, 同时θ1∈[210, 300]时, ALS的变异系数也较大。从图 8c)~8d)中可以看出, ALS失效概率函数在θ2∈[10, 13]和θ2∈[21, 25]时存在显著误差, 同时θ2∈[10, 13.5]和θ2∈[20, 25]时, ALS的变异系数也明显较大, 反观本文提出的AALS方法的变异系数始终保持在0.2以下。综合图 8这4幅图来看, 本文提出的AALS方法获得了与重要抽样法IS结果较一致的“精确”结果, 并且所提出的AALS方法在大部分设计区域拥有相对较小的变异系数。这说明本文提出的AALS方法相较于ALS方法更加高效和稳定。
|
| 图 8 不同方法的失效概率函数结果对比(算例2) |
本文提出了一种全局失效概率函数估计的自适应增强线抽样方法。该方法通过一系列的失效概率函数的局部估计, 以最优组合的方式来融合得到全局失效概率函数, 并提出了一种自适应算法能够自动确定局部估计的位置。本文所提方法能够自动识别并探索弥补估计不足之处, 从而最终达到失效概率函数估计在全设计域上的收敛。
通过本文中给出的算例和结果, 可以得出以下结论:
1) 所提出的自适应策略能够有效地识别出, 能使下一个失效概率函数估计得到最大改善的位置;
2) 提出的最小化失效概率函数估计的变异系数的最优组合算法能够很好地融合各个局部失效概率估计;
3) 所提方法能够克服原有增强线抽样方法的局部性, 且使得失效概率函数的求解能够保证全局上的效率和精度最优。
附录A: 基于最小变异系数的权值在本附录中, 推导基于最小化变异系数的最优权值由公式(21)给出。
首先, 失效概率函数估计的变异系数可以通过以下方式给出
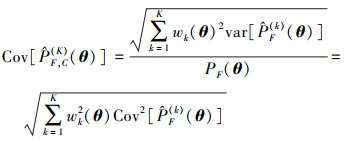
|
(A.1) |
由于最小化Cov[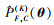
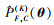
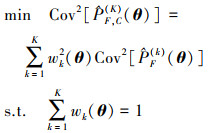
|
(A.2) |
解这一优化问题会得到下列解的表达式

|
(A.3) |
最后, 可得到对应权重值为
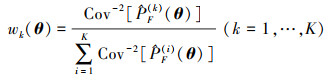
|
(A.4) |
| [1] | FAES M, MOENS D. Recent trends in the modeling and quantification of non-probabilistic uncertainty[J]. Archives of Computational Methods in Engineering, 2020, 27: 633-671. DOI:10.1007/s11831-019-09327-x |
| [2] | VALDEBENITO M A, JENSEN H A, HERNANDEZ H B, et al. Sensitivity estimation of failure probability applying line sampling[J]. Reliability Engineering & System Safety, 2018, 171: 99-111. |
| [3] | YUAN X, FAES M, VALDEBENITO M, et al. Efficient imprecise reliability analysis using the augmented space integral[J]. Reliability Engineering & System Safety, 2021, 210: 107477. |
| [4] | VALDEBENITO M A, SCHUELLER G I. A survey on approaches for reliability-based optimization[J]. Structural and Multidisciplinary Optimization, 2010, 42(5): 645-663. DOI:10.1007/s00158-010-0518-6 |
| [5] | RACKWITZ R, FLESSLER B. Structural reliability under combined random load sequences[J]. Computers & Structures, 1978, 9(5): 489-494. |
| [6] | METROPOLIS N. The beginning of the monte carlo method[J]. Los Alamos Science, 1987, 14: 125-130. |
| [7] | YUAN X, LIU S, FAES M, et al. An efficient importance sampling approach for reliability analysis of time-variant structures subject to time-dependent stochastic load[J]. Mechanical Systems and Signal Processing, 2021, 159: 107699. DOI:10.1016/j.ymssp.2021.107699 |
| [8] | AU S K, BECK J L. Estimation of small failure probabilities in high dimensions by subset simulation[J]. Probabilistic Engineering Mechanics, 2001, 16(4): 263-277. DOI:10.1016/S0266-8920(01)00019-4 |
| [9] | VALDEBENITO M, WEI P, SONG J, et al. Failure probability estimation of a class of series systems by multidomain line sampling[J]. Reliability Engineering & System Safety, 2021, 213: 107673. |
| [10] | GASSER M, SCHUELLER G I. Reliability-based optimization of structural systems[J]. Mathematical Methods of Operations Research, 1997, 46(3): 287-307. DOI:10.1007/BF01194858 |
| [11] | JENSEN H A. Structural optimization of linear dynamical systems under stochastic excitation: a moving reliability database approach[J]. Computer Methods in Applied Mechanics & Engineering, 2005, 194(12/13/14/15/16): 1757-1778. |
| [12] | KAYMAZ I. Application of Kriging method to structural reliability problems[J]. Structural Safety, 2005, 27(2): 133-151. DOI:10.1016/j.strusafe.2004.09.001 |
| [13] | CORTES C, VAPNIK V. Support-vector networks[J]. Machine Learning, 1995, 20(3): 273-297. |
| [14] | ECHARD B, GAYTON N, LEMAIRE M. AK-MCS: an active learning reliability method combining Kriging and Monte Carlo simulation[J]. Structural Safety, 2011, 33(2): 145-154. DOI:10.1016/j.strusafe.2011.01.002 |
| [15] | ZOU T, MAHADEVAN S. A direct decoupling approach for efficient reliability-based design optimization[J]. Structural and Multidisciplinary Optimization, 2006, 31: 190. DOI:10.1007/s00158-005-0572-7 |
| [16] | YUAN X. Local estimation of failure probability function by weighted approach[J]. Probabilistic Engineering Mechanics, 2013, 34: 1-11. DOI:10.1016/j.probengmech.2013.05.001 |
| [17] | YUAN X, ZHENG Z, ZHANG B. Augmented line sampling for approximation of failure probability function in reliability-based analysis[J]. Applied Mathematical Modelling, 2020, 80: 895-910. DOI:10.1016/j.apm.2019.11.009 |
| [18] | SONG J, WEI P, VALDEBENITO M A, et al. Non-intrusive imprecise stochastic simulation by line sampling[J]. Structural Safety, 2020, 84: 101936. DOI:10.1016/j.strusafe.2020.101936 |
| [19] | AU S K. Reliability-based design sensitivity by efficient simulation[J]. Computers & Structures, 2005, 83(14): 1048-1061. |
| [20] | CHING J, HSIEH Y H. Local estimation of failure probability function and its confidence interval with maximum entropy principle[J]. Probabilistic Engineering Mechanics, 2007, 22(1): 39-49. DOI:10.1016/j.probengmech.2006.05.002 |
| [21] | CHING J, HSIEH Y H. Approximate reliability-based optimization using a three-step approach based on subset simulation[J]. Journal of Engineering Mechanics, 2007, 133(4): 481-493. DOI:10.1061/(ASCE)0733-9399(2007)133:4(481) |
| [22] | YUAN X, LIU S, VALDEBENITO M A, et al. Efficient framework for failure probability function estimation in augmented space[J]. Structural Safety, 2021, 92(3): 102104. |




