2. 西北工业大学 民航学院, 陕西 西安 710072;
3. 西安理工大学 机械与精密仪器工程学院, 陕西 西安 710048;
4. 深圳职业技术学院 传播工程学院, 广东 深圳 518000
专色由基色油墨混合调配而成, 可以实现定制要求。为了配置出饱和度更高、色域广的专色, 通常将青色(cyan, C)、品红(magenta, M)、黄色(yellow, Y)、橙色(orange, O)、蓝色(blue, B)和红色(red, R)定义为基色。在获得更高品质专色的同时, 也对专色的复现提出了更高的挑战。准确的专色预测, 可以提高配色效率, 节约试制成本。
目前国内外应用最为广泛的配色理论是Kulbelka-Munk理论, 该理论认为染料浓度的线性增加导致色彩的线性增加[1]。此外配色理论还有密度配色方法[2]、三刺激值配色方法[3]、Stearns-Noechel配色模型[4]、Friele配色模型[5]和Munsell配色模型[6]。然而, 专色的调配是个复杂的过程, 多重变量影响着专色的颜色表达, 专色颜色的变化与染料浓度的变化并非完全线性相关。且上述模型和方法主要应用在不透明的印刷材料上, 并以反射光谱作为模型的理论基础。
PET聚酯薄膜由聚对苯二甲酸乙二醇酯为原料制成, 因其优良的机械性能、较好的耐热性、耐寒性、耐油性和不惧腐蚀等特性, 常作为薄膜印刷基材[7]。PET薄膜因其高透光性, 致使基于反射光谱的配色方法在色彩预测中精度不高。所以目前PET薄膜配色多以人工经验为主, 既增加了配色成本, 又降低了生产效率。因此, 为了提高PET薄膜的配色效率和准确度, 应找到更有效的解决方法。
最小二乘法被广泛应用于参数识别领域[8]。如在Pesal等[9]建立的Kubelka-Munk色彩匹配模型中, 采用最小二乘法预测色素浓度。近年来, 许多研究采用进化算法实现专色配方预测。如Kandi和Tehran[10]采用遗传算法结合粒子群算法对专色配方进行预测。Sabrine等[11]采用蚁群优化算法对专色配方进行预测。尽管专色配方预测取得了成功, 但依旧存在些许缺陷。例如, 为了得到更准确的预测结果, 在预测之前需要采用人工手段对光谱范围和最佳特征进行遴选。此外, 由于进化算法存在早熟和陷入局部最优问题, 色彩预测效果并不稳定。因此, 本文致力于研究一种高效的方法解决这些缺陷, 并实现准确的专色预测。
天牛须搜索算法(beetle antennae search algorithm, BAS) 是一种单体搜索算法, 具有原理简单、参数少、计算量少等优点, 在处理低维优化目标时具有非常大的优势。但是天牛须算法的搜索能力不足, 收敛速度较慢, 易陷入局部最优。
本文主要对PET薄膜印刷制品进行专色配方预测。为了消除基底反射的影响, 采用吸光度构建专色配方预测模型。为了提高专色配方预测的性能, 提升搜索效率, 首先, 使用最小二乘法筛选专色的组成基色。然后, 提出增强天牛须搜索算法, 通过设计突变概率和方向修正项, 克服算法易陷入局部最优的问题, 提高算法收敛速度。最后, 将所提方法应用于20组专色预测, 并与传统天牛须搜索算法、粒子群优化算法和蚁群算法进行对比。结果表明, 相比于传统预测方法, 本文所提出的结合最小二乘法和增强天牛须搜索算法的专色预测方法能够更准确、有效地预测专色配方。
1 油墨吸光度计算方法物质对光的吸收和反射, 是物质呈现出不同颜色的根本原因。朗伯比尔定律[12]描述了物质对光的吸收能力与吸光物质浓度及其介质厚度间的关系。对于高透光薄膜印品, 根据朗伯比尔定律有
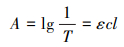
|
(1) |
式中:A为吸光度; T为透射率; ε为摩尔吸收系数; c为物质的摩尔浓度; l为吸光层的厚度。对于由N种基色制备的专色, 其光谱透射率为
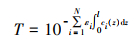
|
(2) |
则推导可得混合油墨的吸光度性质
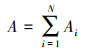
|
(3) |
式中,Ai为某一基色的吸光度。可通过专色吸光度来求解各个组成部分的浓度, 进而获得专色配方。
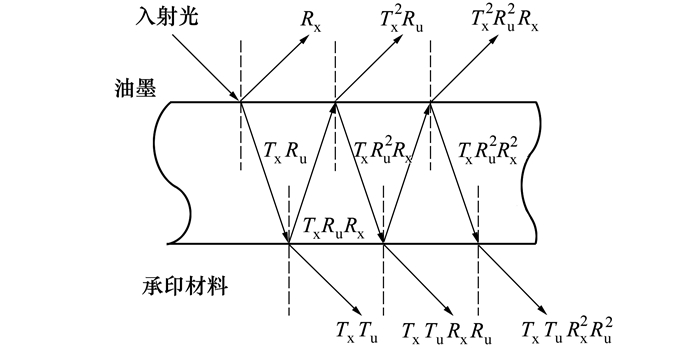
为获得准确的专色配方, 需采集专色和基色油墨的吸收光谱。对于半透明印刷制品而言, 上层介质是油墨, 下层介质是承印材料, 当光照射该印刷制品时, 部分光线在油墨表面反射, 部分光线穿透油墨层进入半透明承印材料中继续传播。传播过程中发生多次折射和反射现象, 其传播过程如图 1所示。
|
| 图 1 光线传播示意图 |
图 1中Rx表示油墨的光谱反射率, Tx表示油墨的光谱透射率, Ru和Tu分别表示承印材料的光谱反射率和光谱透射率。则墨层和承印材料的总光谱反射率Rxu为

|
(4) |
油墨和承印材料的总光谱透射率Txu为
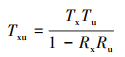
|
(5) |
则可使用(6)~(7)式计算油墨的光谱反射率Rx和光谱透射率Tx

|
(6) |
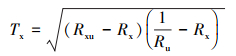
|
(7) |
为了求解Rx和Tx, 把油墨分别打印在白色基底和黑色基底上。定义白色基底的光谱反射率为Ruw, 黑色基底的光谱反射率为Rub; 白色基底的综合光谱反射数据定义为Rxw, 黑色基底的综合光谱反射数据定义为Rxb, 则可推导出

|
(8) |
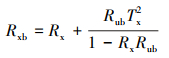
|
(9) |
基于上述推导分析, 可得反射光谱Rx为
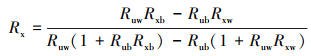
|
(10) |
透射光谱Tx为
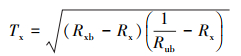
|
(11) |
得到油墨的反射光谱Rx和透射光谱Tx后, 根据朗伯比尔定律, 可得到油墨的吸光度A。
2 增强的天牛须算法天牛须算法是由Jiang等[13]于2017年提出的一种智能优化算法, 与其他仿生算法不同, 天牛须算法是一种单体搜索算法。并且因其参数少, 计算量小的特点, 在处理低维优化目标时有较大的优势。
天牛须搜索算法模仿了自然界中天牛的觅食行为。在天牛觅食过程中, 天牛通过2只触角感知食物的特殊气味。因2只触角感知到的气味浓度有差异, 天牛将向气味浓度高的一侧进行搜索, 寻找食物。通过迭代更新天牛须的位置找到食物所在。
传统天牛须算法流程如下:
第一步, 确定天牛在D维空间的位置, 记为
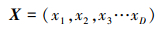
|
(12) |
第二步, 定义天牛2只触角的位置
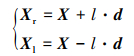
|
(13) |
式中, Xr和Xl表示天牛2只触角的位置; l表示天牛质心与触角的距离; d为单位向量
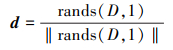
|
(14) |
第三步, 根据2只触角感知到的浓度差, 确定天牛下一步的位置Xt+1
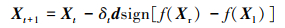
|
(15) |
式中: t为当前迭代次数; f(·)为适应度函数; δt为第t次迭代搜索步长; sign[·]为符号函数; 为提高算法局部搜索能力, 每次迭代后搜索步长都将缩小。因此δt+1=δt·η, η为衰退常数, 通常η=0.95。
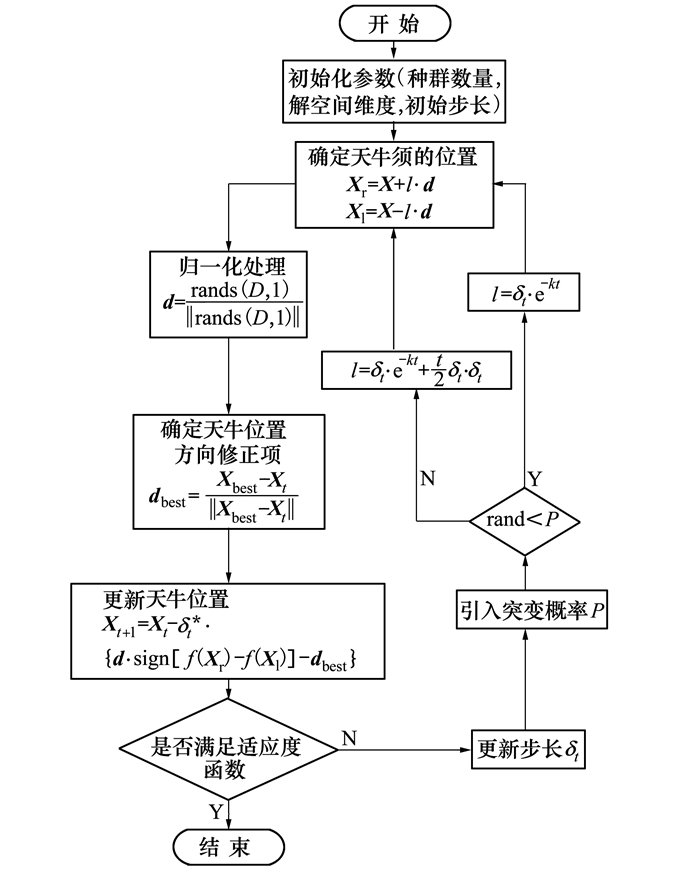
传统天牛须算法采用随机方向虽然提升了算法的全局搜索能力, 但同时也降低了算法的收敛速度。此外, 传统天牛须算法随着迭代次数增加, 搜索步长减小, 虽然有助于增强局部搜索能力, 但同时也致使算法易陷入局部最优。针对上述问题, 本文提出了增强天牛须搜索算法, 增强天牛须算法搜索流程如图 2所示。
|
| 图 2 增强天牛须算法流程图 |
具体计算方法如下:
1) 通过在传统天牛须算法第二步的基础上, 增加突变概率项P, 改变了天牛质心与触角的距离l, 实现了搜索范围的增长突变, 降低了算法陷入局部最优的可能。则天牛2只触角的位置变为
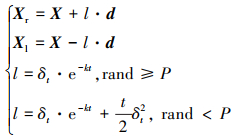
|
(16) |
式中: δt为第t次迭代所探索的步长; P表示算法突变概率; rand为随机数,用于依概率控制步长的突变; k为变化率因子。
2) 通过在传统天牛须算法第三步, 增加方向修正项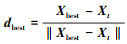
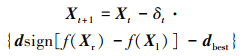
|
(17) |
Xbest为天牛曾出现过的最优位置; Xt为天牛当前位置, 当f(Xt) < f(Xbest)时, 将Xt赋值给Xbest。
3 专色配方预测方法本文将青色、洋红、黄色、橙色、蓝色和红色定义为基色。与四色打印相比, 6种基色打印色域更广。专色配方预测作为专色复现的核心技术, 直接决定了专色复现的准确性。因此, 确定专色的组成基色, 是提高专色配方预测性能的重要环节。
本文提出了一种基于最小二乘法与增强天牛须搜索算法的专色配方预测方法。
第一步, 采用最小二乘法分析专色的基色构成。6种基色的吸收光谱定义为{Ai, i=1, 2, …, 6}。专色的吸收光谱满足(18)式
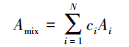
|
(18) |
式中, N为基色的数量。那么各组成基色的摩尔浓度C={ci, i=1, 2, …, N}可使用最小二乘法计算
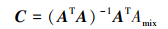
|
(19) |
各基色的摩尔浓度应满足ci≥0。当计算结果ci < 0时, 该基色与目标专色无关, 即可将该基色对应的Ai从矩阵A中剔除, 再重新使用最小二乘法计算摩尔浓度C。若重新计算所得的摩尔浓度C满足每一个ci≥0的约束条件, 则目标专色由剩余的基色组成。剩余基色构成后续天牛须算法的搜索空间。
第二步, 收集所选基色和专色的吸收光谱, 然后利用增强天牛须搜索算法确定摩尔浓度C, 预测专色的配方。搜索空间为第一步中所选基色的数量, 设计目标函数J和约束条件为
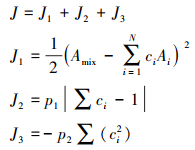
|
(20) |
约束条件
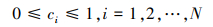
|
式中,J1为均方误差(mean square error, MSE); J2用于控制饱和浓度; J3用于减少配色的基色组成个数; p1和p2为惩罚系数。本文所提的颜色预测方法可以有效减少基色的选择空间, 增强颜色预测的准确性。
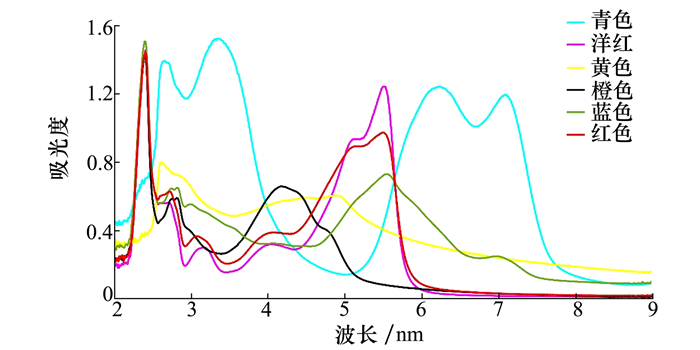
4 实验和结果分析采用英国RK公司凹版印刷机在0.15 mm的PET透明薄膜上进行打印实验。采用瑞士梅特勒托利多公司的ME204电子平衡器, 根据颜色配方称重基色油墨。采用日本岛津公司的紫外分光光度计[14]测量透射光谱和吸收光谱。测量了6种基色在200~900 nm波长范围内的实际吸收光谱, 如图 3所示。
|
| 图 3 吸收光谱图 |
本文对多种专色配方进行实验。专色打印在PET透明薄膜上, 利用岛津紫外可见分光光度计获得专色的吸收光谱。粒子群算法与蚁群算法是进化算法中经典的方法, 被广泛应用于各类优化问题的求解。为了验证本文所提算法的性能, 将本文所提算法与传统天牛须算法、粒子群算法[15-16]和蚁群算法[17]进行比较。4种方法在搭载AMD Ryzen 7 4800H芯片的电脑中执行。根据测量的吸收光谱, 可以发现均方误差J1小于0.2。因此, 目标函数的惩罚因子p1和p2的设置应小于0.1, 否则正则化项J2和约束条件J3将严重影响均方误差项。为了平衡均方误差项, 得到准确的配方, 本文将惩罚因子p1和p2分别设置为0.002和0.000 5。
本文设计了20种专色配方, 其中S1、S2为混合了2种基色的专色配方, S3~S11为混合了3种基色的专色配方, S11~S20为混合了4种基色的专色配方。单一基色与全部基色构成专色无需本文所提方法进行预测, 且5种基色所构成专色配方的搜索难度与4种基色的专色配方类似, 因此此处未设计上述3种配方。表 1列出了S1~S20的定义配方。本文将3种比较算法的种群大小均设置为20,迭代次数为1 000, 以便对比各算法收敛性。
| 编号 | C | M | Y | O | B | R | 编号 | C | M | Y | O | B | R | |
| S1 | 0.2 | 0.8 | 0 | 0 | 0 | 0 | S11 | 0 | 0 | 0 | 0.1 | 0.1 | 0.8 | |
| S2 | 0 | 0 | 0.9 | 0 | 0 | 0.1 | S12 | 0.5 | 0 | 0.2 | 0.2 | 0.1 | 0 | |
| S3 | 0 | 0 | 0 | 0.2 | 0.4 | 0.4 | S13 | 0 | 0 | 0.1 | 0.2 | 0.3 | 0.4 | |
| S4 | 0.3 | 0.3 | 0.4 | 0 | 0 | 0 | S14 | 0.2 | 0.2 | 0.2 | 0 | 0.4 | 0 | |
| S5 | 0 | 0 | 0.5 | 0.2 | 0.3 | 0 | S15 | 0 | 0.3 | 0.3 | 0.2 | 0.2 | 0 | |
| S6 | 0.2 | 0 | 0 | 0.6 | 0 | 0.2 | S16 | 0 | 0 | 0.3 | 0.3 | 0.2 | 0.2 | |
| S7 | 0 | 0.6 | 0 | 0 | 0.3 | 0.1 | S17 | 0.6 | 0 | 0 | 0.2 | 0.1 | 0.1 | |
| S8 | 0 | 0 | 0.1 | 0.5 | 0.4 | 0 | S18 | 0.1 | 0.2 | 0 | 0 | 0.3 | 0.4 | |
| S9 | 0 | 0.2 | 0.4 | 0.4 | 0 | 0 | S19 | 0.3 | 0.2 | 0.2 | 0 | 0 | 0.3 | |
| S10 | 0.1 | 0 | 0 | 0 | 0.5 | 0.4 | S20 | 0.15 | 0.45 | 0.2 | 0.2 | 0 | 0 |
为了获得合理的颜色预测结果, 4种算法均重复20次。4种算法预测配方的平均值X1~X20列于表 2中, 表 3列出预测结果的均方误差MSE和标准差Std。
| 编号 | 本文算法 | 传统天牛须算法 | 蚁群算法 | 粒子群算法 |
| X1 | 0.2∶0.8∶0∶0∶0∶0 | 0.199∶0.799∶0∶0∶0∶0.002 | 0.16∶0.55∶0∶0∶0.08∶0.21 | 0.2∶0.8∶0∶0∶0∶0 |
| X2 | 0∶0∶0.9∶0∶0∶0.1 | 0∶0∶0.9∶0.001∶0.001∶0.098 | 0∶0.07∶0.88∶0∶0∶0.05 | 0∶0.043∶0.9∶0∶0∶0.05 |
| X3 | 0∶0∶0∶0.199∶ 0.401∶0.4 | 0∶0∶0∶0.199∶0.414∶0.388 | 0∶0.1∶0∶0.2∶0.4∶0.3 | 0∶0.24∶0∶0.25∶0.33∶0.18 |
| X4 | 0.3∶0.3∶0.4∶0∶0∶0 | 0.299∶0.304∶0.389∶0.02∶0∶0 | 0.27∶0.28∶0.37∶0.08∶0∶0 | 0.3∶0.3∶0.4∶0∶0∶0 |
| X5 | 0∶0∶0.5∶0.2∶0.3∶0 | 0∶0.493∶0.199∶0.311∶0∶0 | 0∶0.47∶0.2∶0.25∶0.05∶0.03 | 0∶0.5∶0.2∶0.3∶0∶0 |
| X6 | 0.2∶0∶0∶0.6∶0∶0.2 | 0.201∶0∶0∶0.61∶0∶0.19 | 0.17∶0∶0∶0.6∶0.07∶0.16 | 0.18∶0∶0∶0.61∶0∶0.21 |
| X7 | 0∶0.6∶0∶0∶0.3∶0.1 | 0∶0.59∶0∶0.01∶0.28∶0.12 | 0∶0.5∶0∶0∶0.26∶0.24 | 0∶0.6∶0∶0∶0.3∶0.1 |
| X8 | 0∶0∶0.1∶0.501∶0.399∶0 | 0∶0.01∶0.11∶0.51∶0.37∶0 | 0∶0.06∶0.1∶0.56∶0.28∶0 | 0∶0.02∶0.1∶0.53∶0.35∶0 |
| X9 | 0∶0.205∶0.4∶0.395∶0∶0 | 0.008∶0.19∶0.405∶0.397∶0∶0 | 0∶0.1∶0.39∶0.38∶0∶0.13 | 0∶0.2∶0.4∶0.4∶0∶0 |
| X10 | 0.11∶0∶0∶0∶0.49∶0.4 | 0.096∶0∶0∶0.07∶0.47∶0.364 | 0.13∶0∶0.02∶0.02∶0.45∶0.38 | 0.13∶0∶0∶0∶0.47∶0.4 |
| X11 | 0∶0∶0∶0.097∶ 0.1∶0.803 | 0∶0∶0∶0.096∶0.09∶0.814 | 0∶0.06∶0∶0.16∶0.1∶0.68 | 0∶0.01∶0∶0.09∶0.08∶0.82 |
| X12 | 0.507∶0∶0.2∶0.2∶ 0.093∶0 | 0.52∶0.001∶0.219∶0.18∶ 0.06∶0.02 | 0.514∶0∶0.171∶0.207∶ 0.075∶0.033 | 0.523∶0∶0.173∶0.213∶ 0.091∶0 |
| X13 | 0∶0∶0.1∶0.21∶0.29∶0.4 | 0∶0.001∶0.104∶0.206∶ 0.291∶0.398 | 0∶0∶0.11∶0.21∶0.31∶0.37 | 0∶0.09∶0.11∶0.23∶0∶ 0.291∶0.279 |
| X14 | 0.205∶0.2∶0.201∶ 0∶0.394∶0 | 0.22∶0.19∶0.18∶ 0.05∶0.36∶0 | 0.24∶0.16∶0.2∶0.01∶0.39∶0 | 0.225∶0.146∶0.233∶ 0∶0.37∶0.026 |
| X15 | 0∶0.305∶0.3∶0.203∶ 0.192∶0 | 0∶0.283∶0.286∶0.206∶0.225∶0 | 0.02∶0.26∶0.246∶0.205∶ 0.18∶0.089 | 0∶0.3∶0.3∶0.2∶0.2∶0 |
| X16 | 0∶0∶0.3∶0.3∶0.2∶0.2 | 0.01∶0.01∶0.29∶0.29∶0.2∶0.2 | 0∶0.08∶0.31∶0.32∶0.14∶0.15 | 0∶0∶0.33∶0.31∶0.16∶0.2 |
| X17 | 0.6∶0∶0∶0.2∶0.1∶0.1 | 0.58∶0.01∶0.01∶0.2∶0.1∶0.1 | 0.59∶0.01∶0.02∶0.18∶0.1∶0.1 | 0.644∶0∶0∶0.084∶0∶0.272 |
| X18 | 0.1∶0.2∶0∶0∶0.3∶0.4 | 0.1∶0.2∶0.02∶0∶0.29∶0.39 | 0.1∶0.3∶0∶0∶0.28∶0.32 | 0.1∶0.22∶0∶0∶0.3∶0.38 |
| X19 | 0.301∶0.2∶0.199∶ 0∶0∶0.3 | 0.3∶0.2∶0.19∶0.01∶0∶0.3 | 0.28∶0.23∶0.21∶0∶0.06∶0.22 | 0.294∶0.258∶0.223∶0∶ 0.011∶0.22 |
| X20 | 0.149∶0.451∶0.2∶ 0.2∶0∶0 | 0.159∶0.445∶0.202∶ 0.187∶0∶0 | 0.13∶0.4∶0.2∶0.2∶0.02∶0.05 | 0.159∶0.321∶0.15∶ 0.177∶0.008∶0.165 |
| 编号 | 本文算法 | 传统天牛须算法 | 蚁群算法 | 粒子群算法 | |||||||
| MSE | Std | MSE | Std | MSE | Std | MSE | Std | ||||
| X1 | 8.71×10-7 | 9.55×10-7 | 3.13×10-5 | 6.28×10-6 | 5.85×10-4 | 1.55×10-4 | 1.57×10-19 | 6.81×10-20 | |||
| X2 | 1.02×10-4 | 5.63×10-5 | 6.31×10-4 | 2.03×10-4 | 2.38×10-4 | 2.60×10-4 | 3.76×10-4 | 8.84×10-6 | |||
| X3 | 2.74×10-5 | 7.93×10-6 | 1.62×10-4 | 2.68×10-5 | 5.14×10-4 | 2.40×10-4 | 1.49×10-3 | 6.05×10-4 | |||
| X4 | 1.65×10-4 | 3.28×10-5 | 9.57×10-4 | 2.11×10-4 | 3.06×10-3 | 9.77×10-5 | 1.62×10-19 | 9.46×10-5 | |||
| X5 | 1.25×10-4 | 9.24×10-6 | 1.34×10-4 | 2.89×10-5 | 1.08×10-3 | 2.07×10-4 | 1.29×10-19 | 4.92×10-4 | |||
| X6 | 1.35×10-4 | 4.19×10-5 | 7.29×10-4 | 1.68×10-4 | 9.00×10-3 | 2.21×10-4 | 1.09×10-2 | 5.97×10-4 | |||
| X7 | 1.04×10-4 | 2.84×10-5 | 1.72×10-3 | 4.81×10-4 | 2.22×10-4 | 2.89×10-4 | 7.93×10-20 | 6.15×10-4 | |||
| X8 | 1.14×10-4 | 2.82×10-5 | 7.26×10-4 | 1.48×10-4 | 2.38×10-4 | 2.86×10-4 | 3.80×10-3 | 3.61×10-4 | |||
| X9 | 3.80×10-5 | 2.45×10-5 | 1.40×10-3 | 3.17×10-4 | 2.54×10-5 | 3.23×10-5 | 1.45×10-19 | 2.76×10-5 | |||
| X10 | 7.04×10-5 | 1.80×10-5 | 1.05×10-3 | 2.25×10-5 | 2.66×10-4 | 2.22×10-4 | 2.00×10-3 | 2.33×10-4 | |||
| X11 | 2.05×10-6 | 8.83×10-6 | 1.77×10-4 | 2.26×10-5 | 5.74×10-4 | 1.93×10-4 | 2.39×10-4 | 1.85×10-4 | |||
| X12 | 2.04×10-4 | 1.05×10-4 | 2.33×10-3 | 3.91×10-4 | 4.44×10-3 | 4.33×10-4 | 7.01×10-5 | 7.26×10-4 | |||
| X13 | 1.04×10-4 | 3.70×10-5 | 5.86×10-4 | 1.23×10-4 | 2.50×10-3 | 6.00×10-4 | 9.22×10-4 | 5.86×10-4 | |||
| X14 | 1.09×10-4 | 5.44×10-5 | 1.70×10-3 | 3.66×10-4 | 2.08×10-4 | 3.52×10-4 | 1.20×10-3 | 3.61×10-4 | |||
| X15 | 1.03×10-4 | 2.21×10-5 | 7.24×10-4 | 1.61×10-4 | 1.30×10-3 | 6.03×10-4 | 3.65×10-19 | 3.43×10-4 | |||
| X16 | 5.13×10-4 | 5.57×10-5 | 3.73×10-3 | 6.18×10-4 | 8.70×10-3 | 3.27×10-4 | 2.57×10-2 | 5.00×10-4 | |||
| X17 | 6.92×10-4 | 1.16×10-4 | 9.19×10-3 | 1.82×10-3 | 1.35×10-3 | 3.77×10-4 | 1.80×10-3 | 4.54×10-4 | |||
| X18 | 3.83×10-4 | 7.98×10-5 | 3.41×10-3 | 5.99×10-4 | 2.54×10-5 | 1.20×10-4 | 9.50×10-4 | 2.20×10-4 | |||
| X19 | 3.19×10-4 | 4.02×10-5 | 1.17×10-3 | 3.18×10-4 | 6.08×10-5 | 9.16×10-5 | 5.69×10-4 | 4.80×10-5 | |||
| X20 | 3.01×10-4 | 4.62×10-5 | 7.43×10-4 | 8.23×10-5 | 7.69×10-5 | 1.87×10-4 | 9.23×10-4 | 3.61×10-4 | |||
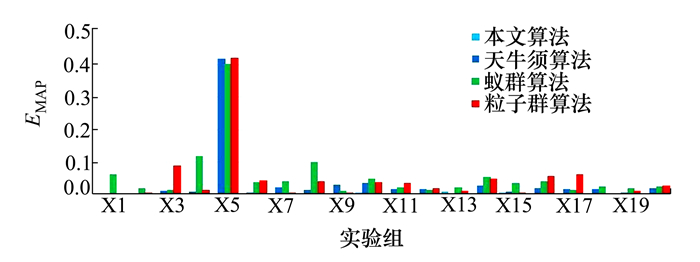
图 4显示了预测结果的平均绝对百分比误差[18] 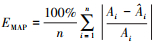
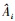
|
| 图 4 不同算法平均绝对百分比误差 |
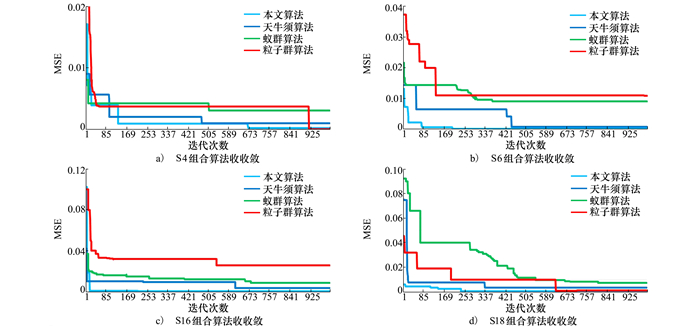
为简便起见, 图 5展示了4种算法在专色S4、S6、S16和S18上的收敛曲线。从图 5可以看出, 与其他3种方法相比, 本文所提方法得到最优解的迭代次数更少, 收敛速度更快。
|
| 图 5 收敛曲线(S4、S6、S16、S18) |
为了更直观地比较4种算法的预测结果, 本文使用色差ΔE进行进一步比较。色差ΔE计算过程如下。首先使用标准红绿蓝值(standard red green blue, sRGB)计算出CIE XYZ。
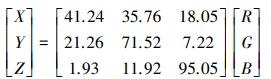
|
(21) |
然后, 通过CIE XYZ颜色值的非线性变化, 得到CIE lab的颜色值, 如(22)式所示
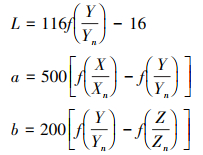
|
(22) |
式中,Xn, Yn, Zn是标准白点的三刺激值。非线性变化的定义如(23)式所示
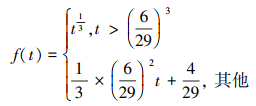
|
(23) |
那么, 色差[19]ΔE可以通过(24)式得到
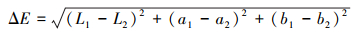
|
(24) |
表 4中列出了预设专色和预测专色的色差值ΔE, ΔE越大表示色差越大。
| ΔE | 本文算法 | 天牛须算法 | 蚁群算法 | 粒子群算法 |
| X1 | 0.146 | 0.081 | 9.319 | 0.212 |
| X2 | 0.738 | 0.173 | 12.283 | 7.928 |
| X3 | 0.141 | 2.964 | 6.587 | 7.484 |
| X4 | 0.051 | 1.181 | 6.464 | 0.102 |
| X5 | 0.696 | 1.299 | 8.844 | 0.140 |
| X6 | 0.083 | 0.714 | 11.297 | 2.427 |
| X7 | 0.063 | 4.818 | 11.599 | 0.070 |
| X8 | 0.179 | 3.962 | 14.605 | 6.579 |
| X9 | 0.765 | 0.851 | 11.767 | 0.000 |
| X10 | 1.888 | 14.682 | 13.508 | 5.592 |
| X11 | 0.440 | 2.629 | 8.936 | 3.942 |
| X12 | 0.774 | 4.010 | 2.747 | 0.616 |
| X13 | 2.324 | 2.014 | 2.934 | 5.839 |
| X14 | 0.905 | 8.954 | 6.705 | 9.259 |
| X15 | 0.934 | 2.331 | 5.037 | 0.000 |
| X16 | 0.063 | 2.243 | 5.024 | 8.647 |
| X17 | 0.065 | 1.114 | 0.952 | 8.894 |
| X18 | 0.065 | 3.647 | 4.008 | 1.348 |
| X19 | 0.073 | 0.346 | 10.388 | 5.696 |
| X20 | 0.068 | 1.067 | 2.830 | 7.979 |
通过表 4可知, 本文算法所预测专色与预设配方专色无明显差异, 预设专色和预测专色之间色差均小于3, 其中90%的色差小于1, 40%的色差小于0.1, 均满足无色差忠实复制要求[20]; 传统天牛须算法预测专色与预设配方专色X10色差达到14.682, X14达到8.954,不满足专色复制要求; 蚁群算法的X6~X10和粒子群算法的X14、X16、X17与相应的预设配方相比有明显的颜色差异, 且蚁群的算法的X8色差值为14.605, 粒子群算法X14的色差值为9.259, 不满足专色复制要求[20]。
综合上述实验结果表明, 本文所提方法在4种方法中具有最好的专色配方预测性能。
5 结论本文提出了一种寻找专色配方的颜色预测方法。首先, 提出了一个基于吸收光谱的机理模型来描述基色和专色的关系。然后, 采用最小二乘法确定构成目标专色的配方所需的基色。最后, 根据筛选的基色, 利用本文所提增强天牛须算法, 实现对专色配方的准确预测。最小二乘法缩小了天牛须算法的搜索空间, 加快了算法收敛速度。
将本文方法与传统天牛须算法、粒子群算法和蚁群算法比较, 验证了所提算法在专色配方预测方面的有效性和优越性。结果表明, 与其他3种方法相比, 本文方法预测准确性更高, 可以有效实现专色配方的预测。本文方法预测专色的结果与所有预设专色之间的色差均小于3, 其中90%的色差小于1, 40%的色差小于0.1。因此, 本文所提方法能够实现对专色配方的准确预测。未来的研究方向会针对不同的PET膜作为承印材料进行专色预测研究。
| [1] | DAI S Y, PAN X N, MA L J, et al. Discovery of the linear region of near infrared diffuse reflectance spectra using the Kubelka-Munk theory[J]. Frontiers in Chemistry, 2018, 6: 154. DOI:10.3389/fchem.2018.00154 |
| [2] | TANG A Y, WANG Y M, LEE C H, et al. Computer color matching and levelness of PEG-based reverse micellar decamethyl cyclopentasiloxane(D5) solvent-assisted reactive dyeing on cotton fiber[J]. Applied Sciences, 2017, 7(7): 682. DOI:10.3390/app7070682 |
| [3] | WEI J, PENG M, LI Q, et al. Evaluation of a novel computer color matching system based on the improved back-propagation neural network model[J]. Journal of Prosthodontics, 2018, 27(8): 775-783. DOI:10.1111/jopr.12561 |
| [4] | DONG M W, BING S Z, MIN Y, et al. Research on application of controlling variables in computer color matching for textile dyeing[J]. Applied Mechanics and Materials, 2014, 3365(602/603/604/605): 878-881. |
| [5] | MIN Y, BING S Z, DONG M W. Research on application of polynomial regression analysis for computer color matching in textile dyeing[J]. Applied Mechanics and Materials, 2014, 3365(602/603/604/605): 719-772. |
| [6] | DIVYESH R P, NAITIK B P, BHAVESH M P, et al. Computer color matching(CCM) data of some newly synthesized acid dyes and their application on polyamide fibres[J]. Proceedings of the National Academy of Sciences, India Section A: Physical Sciences, 2013, 83(4): 287-298. DOI:10.1007/s40010-013-0089-1 |
| [7] | TULEUSHEV A Z, HARRISON F E, KOZLOVSKIY A L, et al. Assessment of the irradiation exposure of PET film with swift heavy ions using the interference-free transmission UV-vis transmission spectra[J]. Polymers, 2021, 13(3): 358. DOI:10.3390/polym13030358 |
| [8] | ZAHID T, LI W. A comparative study based on the least square parameter identification method for state of charge estimation of a LiFePO4 battery pack using three model-based algorithms for electric vehicles[J]. Energies, 2016, 9(9): 720. DOI:10.3390/en9090720 |
| [9] | KOIRALA P, HAUTA-KASARI M, MARTINKAUPPI B, et al. Color mixing and color separation of pigments with concentration prediction[J]. Color Research & Application, 2008, 33(6): 461-469. |
| [10] | KANDI S G, TEHRAN M A. Color recipe prediction by genetic algorithm[J]. Dye Pigm, 2017, 74: 677-683. |
| [11] | SABRINE C, ALI M, IMED B M. Colour recipe prediction using ant colony algorithm: principle of resolution and analysis of performances[J]. Color Technology, 2019, 135: 349-360. DOI:10.1111/cote.12409 |
| [12] | WERNER M, ERHAN D. UV-VIS absorption spectroscopy: lambert-beer reloaded[J]. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 2017, 173: 965-968. DOI:10.1016/j.saa.2016.09.037 |
| [13] | JIANG X Y, LI S. BAS: beetle antennae search algorithm for optimization problems[J]. International Journal of Robotics and Control, 2018, 1(1): 1. DOI:10.5430/ijrc.v1n1p1 |
| [14] |
康文运, 宋小全, 范东启. 可见光/近红外波段多波长皮秒激光研究[J]. 红外与毫米波学报, 2018, 37(4): 433-436.
KANG Wenyun, SONG Xiaoquan, FAN Dongqi. Research on visible/near infrared multi-wavelength picosecond laser[J]. Journal of Infrared and Millimeter Waves, 2018, 37(4): 433-436. (in Chinese) |
| [15] | AL A M, CHEAH W P, TAN S C. Deep autoencoder-based community detection in complex networks with particle swarm optimization and continuation algorithms[J]. Journal of Intelligent & Fuzzy Systems, 2021, 40(3): 4517-4533. |
| [16] | GASMI I, AZIZI M W, SERIDI B H, et al. Enhanced context-aware recommendation using topic modeling and particle swarm optimization[J]. Journal of Intelligent & Fuzzy Systems, 2021, 40(6): 12227-12242. |
| [17] | JIN Y, XIAO M Y, SHENG L. Dynamic reproductive ant colony algorithm based on piecewise clustering[J]. Applied Intelligence, 2021, 51(12): 8680-8700. DOI:10.1007/s10489-021-02312-7 |
| [18] | GAO Z H, LIU Y, WANG Q J, et al. Ensemble empirical mode decomposition energy moment entropy and enhanced long short-term memory for early fault prediction of bearing[J]. Measurement, 2022, 188: 110417. DOI:10.1016/j.measurement.2021.110417 |
| [19] | HOLM J, DYER S, SHERLOCK D. Illumination source metrics and color difference-selecting sources for cinematography[C]//Proceedings of the Color and Imaging Conference, 2018 |
| [20] |
张研, 周世生, 曹从军, 等. 基于吸光度的PET薄膜专色配方预测方法[J]. 光谱学与光谱分析, 2019, 39(2): 415-420.
ZHANG Yan, ZHOU Shisheng, CAO Congjun, et al. Prediction method of PET film spot color formula based on absorbance[J]. Spectroscopy and Spectral Analysis, 2019, 39(2): 415-420. (in Chinese) |
2. School of Civil Aviation, Northwestern Polytechnical University, Xi'an 710072, China;
3. School of Mechanical and Precision Instrument Engineering, Xi'an University of Technology, Xi'an 710048, China;
4. School of Communication Engineering, Shenzhen Polytechnic, Shenzhen 518000, China




