2. 陕西烽火通信集团有限公司, 陕西 宝鸡 721006;
3. 西安石油大学 计算机学院, 陕西 西安 710065
有源噪声控制(active noise control, ANC)是一种有别于传统降噪方法的新型降噪措施, 它通过人为引入的次级声源, 使其辐射声波与原始噪声产生相消性干涉而降噪[1]。自适应控制是ANC系统的主要实现方式, 它通过控制器中的自适应算法自动调节次级声源强度,使降噪效果达到最佳[2]。ANC系统具有质量轻、布置灵活、频带针对性强等优点, 目前已步入工程应用阶段[3-4]。在该系统中, 次级声源如发生故障会使得输出的次级噪声异常, 进而导致降噪效果变差甚至引起系统失稳[5]。由于ANC系统使用环境中通常存在复杂的干扰声, 很难通过人工辨别或自动检测的方式判断其工作状态以及是否发生故障。
次级声源是有源噪声控制系统中重要的换能器件, 往往由特制的低频扬声器组成。虽然由扬声器组成的音响系统广泛用于汽车、飞机、音乐厅等, 但绝大多数情况下人们只关注扬声器自身的声学性能, 针对扬声器故障检测的研究多限于实验室或生产环境下[6], 其主要方法一般都是基于人的听觉检测进行的[7]。
近10年来, 国内外对扬声器的故障检测研究较多, 周静雷等[8]通过检测电信号和声信号判断扬声器是否存在异常音, 是一种典型的在线扬声器故障检测方法。Valk[9]设计了一种反馈控制器, 提高了低音扬声器的声学总谐波失真和低频带宽性能。Venturi等[10]提出一种RLS-NLMS混合自适应算法, 实现了扬声器中音调噪声故障的诊断。同年, 李云红等[11]通过对异音功率谱和掩蔽阈值的比较, 实现了扬声器的异音故障检测。Serban等[12]提出一种基于直接辐射场的实验系统来检测扬声器直接散热器的退化故障。Philip[13]对扬声器的缺陷和不规则行为进行识别, 研究出一种扬声器故障检测的系统识别方法。
ANC系统的复杂性和自适应性要求系统中的次级声源应具有较好的声学性能和高可靠性。这使得对次级声源在工作中的实时故障检测研究显得格外重要。现有的扬声器故障检测方法多针对实验室环境下的产品质量检测或测试, 而少数的在线扬声器故障检测方法计算复杂, 对硬件性能要求高, 且无法满足有源噪声控制中次级声源输出特性, 会增加额外的干扰而影响降噪效果。
本文基于现有的扬声器故障检测研究成果, 提出一种专门用于次级声源故障检测的方法, 目的是在ANC系统工作时, 能够实时检测次级声源是否发生故障。通过采集次级声源的输入电压和输出电流, 对实测的阻抗曲线进行移动平滑滤波处理, 从而得到次级声源的阻抗曲线, 对其指标值进行处理分析, 判断是否发生故障。该方法可以在不影响设备正常工作的情况下, 不借助其他的电声器件和检测仪器, 仍准确实时地判断出次级声源的工作状态。
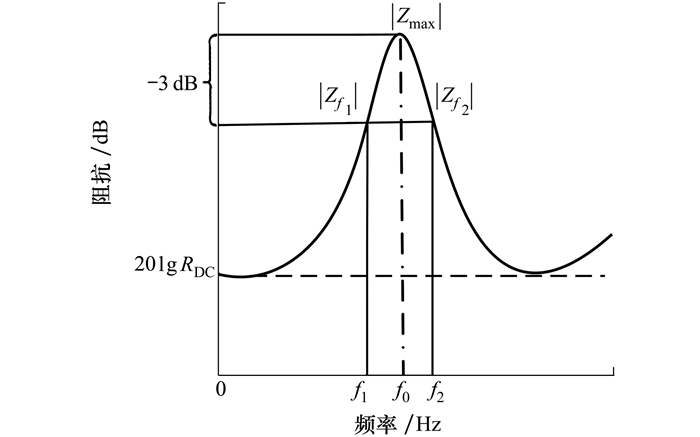
1 故障检测原理 1.1 系统原理次级声源的电学参数主要由电阻抗及其派生特性参数组成, 包括额定阻抗、共振频率和总品质因数等。由于次级声源中音圈的阻抗会随着激励信号频率的不同而呈现不同的幅值, 阻抗模值与频率的关系曲线为阻抗曲线(如图 1所示)。在阻抗曲线上可以得到上述电学参数值, 如次级声源的总品质因数Q和共振频率f0。
|
| 图 1 次级声源阻抗曲线模型 |
总品质因数Q是反映次级声源低频特性的一个重要参数, 它是在次级声源共振频率处声阻抗中惯性抗部分与纯阻部分的比, 计算方法为
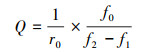
|
(1) |
式中, f1和f2是在阻抗曲线中截取(|Zmax| -3)dB处即|Zf1|和|Zf2|所对应的频率值。r0是f0处次级声源的最大阻抗与次级声源音圈直流电阻RDC之间的比值。f0是阻抗曲线第一个极大值对应的频率值。f0的计算公式为
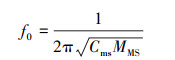
|
(2) |
式中:MMS=MS+MV+MA, MS为静止状态的纸盆质量; MV为音圈的质量; MA=MMDSD2, 为同振动空气的质量, 而MMD=MS+MV, SD为次级声源纸盆的辐射有效面积。即有

|
(3) |
从(3)式中可以看出, 共振频率f0的大小是由折环与定心支片顺性Cms、纸盆质量MS和音圈质量MV所决定。通过对无故障次级声源f0和Q值进行测量, 设定f0和Q值的允许偏差范围, 如超过f0和Q设置的偏差阈值, 就可知是次级声源的某些特征参数发生了变化,从而导致f0和Q值出现异常, 据此判断次级声源的工作状态。
依据上述原理, 本文次级声源故障检测系统微处理可以是DSP、FPGA和STM32单片机等数字信号处理器。电压和电流采集模块通过AD采集将喇叭单元的输入电压和输出电流转换为数字信号输入至微处理器, 作为故障检测的计算数据源。由于AD采集的信号中存在直流偏置, 首先进行均值滤波去除直流偏置, 然后对采集到的电压和电流进行快速傅里叶变换, 将时域信号转换为频域信号, 从而计算得到次级声源的阻抗曲线。再通过移动平均滤波器对阻抗数据进行去噪实现平滑处理。然后使用去噪后的阻抗数据得到次级声源工作时的特征参数。最后根据特征参数变化判断次级声源的工作状态。
1.2 故障类型次级声源故障分为2种:
在生产过程中由于加工操作不当或材料质量问题导致的故障, 包括: ①碰圈: 发声时音圈与导磁柱出现碰撞的情况; ②漏气: 音圈与防尘帽、纸盆与音圈、纸盆与折环之间连接处开胶, 在开胶处会产生异常音。
在次级声源日常使用过程中出现的故障, 包括: ①纸盆破损: 纸盆受潮、老化或功率过大导致纸盆破损; ②折环破裂: 折环长时间工作会出现老化, 失去弹性破裂; ③音圈损坏: 大功率下工作, 音圈烧断、烧毁; ④定心支片破损: 支片受潮、老化或异物导致支片破裂或受损。
根据ANC系统工作过程中次级声源的故障类型分析, 典型的次级声源故障有折环开裂和定心支片破损2种。
1.3 检测方法扬声器的电声转换实际上等效于一个非线性非平稳系统, 传统的傅里叶变换只能处理平稳信号。傅里叶分析是频域分析的基本工具, 为了达到时域的局部化, 在信号傅里叶变换前进行汉宁窗函数处理。本文采用STFT的方法得到扬声器响应的时频特性。STFT是利用一个适当宽度的窗函数, 把信号划分成许多小段, 对每一小段进行傅里叶分析, 得到其局部频谱。STFT能反映频率分量随时间的变化规律, 获得比较好的信号时频特征。
设系统的采样率为Fs, 采样周期为T, 则一个采样周期内的采样点数N为
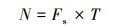
|
(4) |
一个采样周期内的电压和电流可分别表示为:

|
(5) |
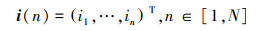
|
(6) |
由于采集电路中存在直流, 需要去除直流偏置, 第n个采样点去除直流偏置的电压和电流分别为:
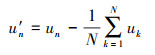
|
(7) |
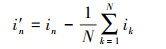
|
(8) |
分别对电压和电流的N个采样点数据进行汉宁窗函数处理后,再使用STFT方法得到扬声器响应的时频特性。电压U和电流I的频域表示为U(f)和I(f)。设H为电压U和电流I在频域中的传递函数, 则有I(f)=H(f)U(f), 传递函数H的估计为
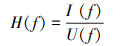
|
(9) |
电阻抗R(f)计算式为
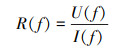
|
(10) |
即
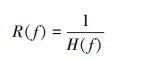
|
(11) |
对R(f)取绝对值并求对数幅度Z(f),如(12)式所示
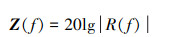
|
(12) |
即

|
(13) |
式中, Z(f)长度为N/2,可表示为
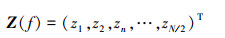
|
(14) |
由于次级声源电声响应中存在干扰音等其他信号, 得到的阻抗曲线并不平滑, 因此需要使用移动平均滤波器对阻抗数据进行平滑处理。移动平滑滤波器基于统计规律, 将连续的采样数据看成一个长度固定的队列, 按照给定的移动窗宽将相邻点的数据依一定方向连续移动进行平均。设移动窗宽为5, 输入信号为x(n), 则经过移动平滑滤波器处理后的输出信号y(n)计算公式为:
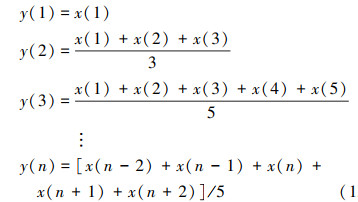
|
(15) |
系统的采样率为Fs, 一个采样周期内的采样点数为N, 通过傅里叶分析后得到的频谱频率分辨率Δf为

|
(16) |
如图 1所示, 可得阻抗曲线Z(f)的最大幅度Zmax值为
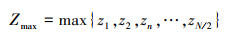
|
(17) |
设n0是Z(f)的最大值Zmax对应的队列序号, 则次级声源的最低共振频率f0为阻抗曲线幅度最大值Zmax对应的频率值, 即有
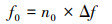
|
(18) |
对于阻抗曲线离线序列Z(f)必然存在序号为n1对应阻抗幅度为Zn1, 且满足(19)式条件的离散点
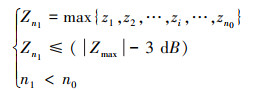
|
(19) |
同理, 对于阻抗曲线离线序列Z f(f)必然存在序号为n2对应阻抗幅度为Zn2, 且满足(20)式条件的离散点
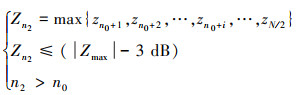
|
(20) |
Zn1和Zn2即为要求的Zf1和Zf2, 则对应f1和f2的值为

|
(21) |
式中, r0是f0处次级声源的最大阻抗与次级声源音圈直流电阻RDC之间的比值, 计算方法为

|
(22) |
至此, 根据(1)式即可求得在次级声源在工作时的实时特征参数值Q。使用实时测得的f0和Q值与标准值的偏差比例作为故障判定依据, 分别记为Δf0和ΔQ, 即
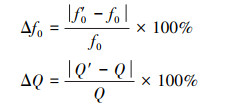
|
(23) |
式中, f′ 0和Q′分别为次级声源工作时实测并计算得的f0和Q值, 当实测值与标准值偏差比例均大于设定阈值时判定次级声源故障, 即次级声源故障判定依据为
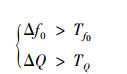
|
(24) |
式中, Tf0和TQ分别为Δf0和ΔQ异常的判定阈值。
2 仿真及实验结果分析 2.1 仿真模型工程应用中次级声源多选用低频性能较好且稳定的扬声器, 因此仿真中更关注次级声源的低频性能变化引起的性能故障。针对无故障次级声源的阻抗特性频响曲线, 对其工作时发生故障引起的阻抗特性参数f0和Q值变化进行计算机仿真。
由(10)式可知, 次级声源的阻抗值由其两端电压U和内部电流I决定。转化为离散信号系统在频域进行分析时, 其阻抗可视为电压U和电流I在频域中的传递函数, 也可视为电流I是电压U经过一个特殊滤波器后的输出。因此次级声源故障可以理解为电压U和电流I信号之间的传递函数发生变化, 即滤波器系数发生变化。
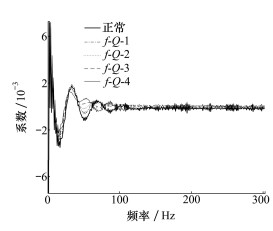
通常次级声源的工作状态发生改变时, 其阻抗特性参数f0和Q值会同时发生变化。图 2为模拟的正常无故障和4种不同损坏程度次级声源的滤波器系数曲线, 曲线f-Q-1、f-Q-2、f-Q-3和f-Q-4分别表示次级声源损坏程度由小变大时的滤波器系数。
|
| 图 2 不同损坏程度次级声源的滤波器系数曲线 |
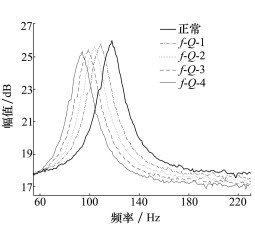
根据图 2所示的滤波器系数曲线可以得到次级声源幅频特性曲线, 如图 3所示。为便于对比, 图 2~3中同时给出了正常次级声源的滤波器系数和幅频特性曲线。
|
| 图 3 不同损坏程度次级声源的幅频特性曲线 |
由图 3的幅频特性曲线可知, 当次级声源发生故障时, 其特征值参数f0发生偏移, 并伴随特征值参数Zmax的变化, 特征值参数Q值也随之发生改变。
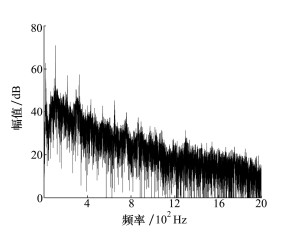
根据ANC系统中次级声源的使用场景, 噪声控制目标通常为低频的线谱噪声, 如涡桨飞机、汽车发动机和变压器噪声等, 或类似粉红噪声的宽频带噪声, 如汽车行驶中的风噪、喷气式飞机和空调管道噪声等。故仿真中分别采用飞机声、粉红噪声、扫频信号和单谱线4种典型噪声信号来激励次级声源, 以研究其在不同激励信号下的阻抗特性曲线差异。由于实际硬件电路中存在一定的底噪, 因此对单谱线噪声加入了信噪比约-35 dB的粉红噪声, 用以模拟实际电路中次级声源输出的背景噪声。飞机声是由多根谱线组成的某型涡桨飞机舱内的实测噪声, 其噪声频谱如图 4所示。
|
| 图 4 涡桨飞机噪声频谱 |
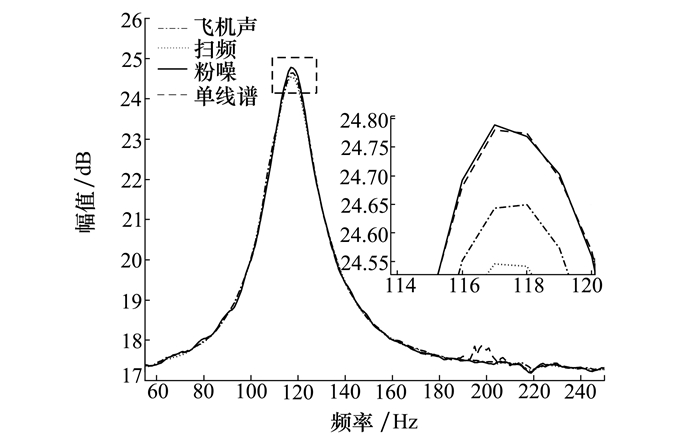
分别使用飞机声、粉红噪声、扫频信号和单线谱4种噪声信号激励正常状态下的次级声源, 计算得到的阻抗曲线如图 5所示。由图可知其4条阻抗曲线接近重合, 特征值参数f0值未发生显著变化。粉红噪声和单线谱噪声激励得到的阻抗曲线在f0处的阻抗值几乎一致, 与飞机声和扫频信号激励得到的阻抗曲线存在细微差异。
|
| 图 5 正常状态不同噪声的阻抗曲线 |
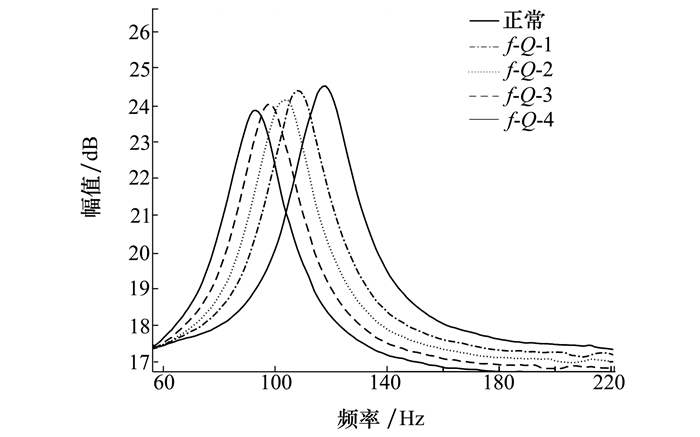
使用飞机声激励不同状态的次级声源, 不同损坏程度其特征值参数值发生显著变化, 考虑到在计算特征值Q时由于阻抗曲线并不光滑, 存在一定的偏差, 故将其经过一个移动平滑滤波器, 移动窗宽设为5, 从而达到曲线平滑的目的, 由此得到更准确的特征值Q。经过移动平滑滤波后的阻抗曲线如图 6所示。由图 6得到其特征值参数(见表 1)。由表 1可知当次级声源的损坏程度越大时, 其特征值参数f0和Q值的偏差也越大。
|
| 图 6 飞机声激励不同状态次级声源阻抗曲线 |
| 损坏状态 | f0/Hz | f1/Hz | f2/Hz | Q | Δf0/% | ΔQ/% |
| f-Q-1 | 109.0 | 97.5 | 121.0 | 1.119 1 | 8.40 | 4.43 |
| f-Q-2 | 105.0 | 92.1 | 116.0 | 1.089 0 | 11.76 | 7.00 |
| f-Q-3 | 99.0 | 87.2 | 110.9 | 1.049 9 | 16.81 | 10.34 |
| f-Q-4 | 94.0 | 81.9 | 105.7 | 1.013 6 | 21.01 | 13.44 |
使用粉红噪声、扫频和单线谱激励下的不同损坏程度次级声源阻抗特征值参数见表 2~4。由表 2和表 4对比可知, 由于2种噪声都包含了粉红噪声成分, 阻抗曲线特征值比较接近。
| 故障状态 | f0/Hz | f1/Hz | f2/Hz | Q | Δf0/% | ΔQ/% |
| f-Q-1 | 109.0 | 97.3 | 121.7 | 1.091 1 | 8.40 | 9.06 |
| f-Q-2 | 104.0 | 91.9 | 116.7 | 1.052 0 | 12.61 | 12.31 |
| f-Q-3 | 99.0 | 86.3 | 111.1 | 1.017 3 | 16.81 | 15.21 |
| f-Q-4 | 94.0 | 81.2 | 105.7 | 0.994 3 | 21.01 | 17.12 |
| 故障状态 | f0/Hz | f1/Hz | f2/Hz | Q | Δf0/% | ΔQ/% |
| f-Q-1 | 109.0 | 97.8 | 120.7 | 1.135 2 | 8.40 | 6.86 |
| f-Q-2 | 104.0 | 92.5 | 115.8 | 1.095 5 | 12.61 | 10.12 |
| f-Q-3 | 99.0 | 87.2 | 110.8 | 1.055 4 | 16.81 | 13.41 |
| f-Q-4 | 94.0 | 81.9 | 105.8 | 1.009 9 | 21.01 | 17.14 |
| 故障状态 | f0/Hz | f1/Hz | f2/Hz | Q | Δf0/% | ΔQ/% |
| f-Q-1 | 109.0 | 100.1 | 119.4 | 1.274 3 | 8.40 | 6.19 |
| f-Q-2 | 107.0 | 92.5 | 116.1 | 1.115 9 | 10.08 | 7.02 |
| f-Q-3 | 97.0 | 86.2 | 113.0 | 0.937 2 | 18.49 | 21.90 |
| f-Q-4 | 94.0 | 81.6 | 106.4 | 0.974 3 | 21.01 | 18.81 |
由表 1~4可知, 不同损坏程度的次级声源, 使用不同噪声信号激励得到的阻抗特征参数变化规律一致, 损坏程度越大, 其特征值参数Δf0和ΔQ的偏差越大。而作为故障检测使用的特征值参数Δf0和ΔQ可以使用粉红噪声、线谱噪声或扫频信号中的任意一种来激励次级声源得到。
2.3 实验验证故障检测所需的数据包括工作时喇叭单元两端的实时输入电压U和输出电流I。实验选择同一型号同一批次的次级声源, 其中直流阻抗值RDC为4 Ω。为模拟降噪时有源控制器给次级声源的输出, 次级声源输入噪声类型分别为粉红噪声、单线谱和飞机噪声。测试次级声源的故障有折环开裂和定心支片破损2种。
分别使用3种噪声测试正常和故障的次级声源, 对实验数据处理得到次级声源阻抗曲线, 得到判断次级声源故障状态所需的计算数据, 代入(1)式和(23)式, 可得不同状态的次级声源特征值参数,见表 5~7。由表 5~7可知, 与正常的次级声源相比, 当次级声源出现不同的故障时, 其特征值参数发生了明显变化。次级声源的损坏程度越大, 特征值参数变化也越大, 因此由次级声源的特征值参数变化程度, 即可判断次级声源的故障状态。
| 故障状态 | f0/Hz | f1/Hz | f2/Hz | Zmax | r0 | Q | Δf0/% | ΔQ/% |
| 正常 | 121.0 | 110.7 | 131.7 | 25.57 | 4.747 2 | 1.213 7 | 0 | 0 |
| 折环开裂 | 92.0 | 82.7 | 101.7 | 25.87 | 4.914 1 | 0.985 3 | 23.97 | 15.73 |
| 定心支片破损 | 101.0 | 91.6 | 110.7 | 25.78 | 4.863 4 | 1.087 3 | 16.53 | 10.41 |
| 故障状态 | f0/Hz | f1/Hz | f2/Hz | Zmax | r0 | Q | Δf0/% | ΔQ/% |
| 正常 | 122.0 | 111.5 | 132.2 | 25.06 | 4.476 5 | 1.316 6 | 0 | 0 |
| 折环开裂 | 90.0 | 80.4 | 100.1 | 25.39 | 4.649 9 | 0.982 5 | 26.23 | 25.38 |
| 定心支片破损 | 100.0 | 90.8 | 110.8 | 25.30 | 4.601 9 | 1.086 5 | 18.03 | 17.48 |
| 故障状态 | f0/Hz | f1/Hz | f2/Hz | Zmax | r0 | Q | Δf0/% | ΔQ/% |
| 正常 | 122.0 | 108.9 | 134.3 | 23.72 | 3.836 5 | 1.252 0 | 0 | 0 |
| 折环开裂 | 94.0 | 83.2 | 104.6 | 24.3 | 4.101 5 | 1.071 0 | 22.95 | 14.46 |
| 定心支片破损 | 95.0 | 84.0 | 107.4 | 23.92 | 3.925 9 | 1.034 1 | 22.13 | 17.40 |
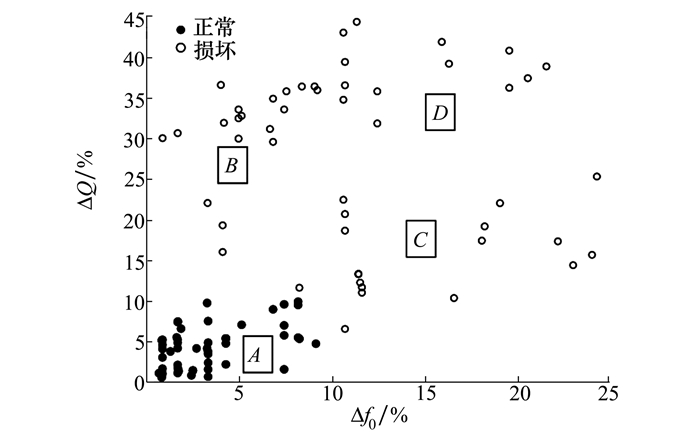
本文通过数值分析论证了使用阻抗曲线特征值参数变化来判断次级声源故障的可行性, 同时进行了实验验证。为研究故障检测阈值与故障检测误报率的关系, 本文选用的次级声源样本数N为100, 其中正常无故障的次级声源样本数N1为50, 不同程度损坏的故障次级声源样本数为50。损坏的次级声源包括折环开裂、定心支片破损和异物压迫等故障, 其损坏和故障程度大小均不相同, 通过听音辨别, 部分轻微故障的次级声源与无故障的次级声源差异并不明显。实验得到的Δf0和ΔQ变化值如图 7所示, 其中实心点表示正常无故障的次级声源, 空心点表示存在不同程度损坏的故障次级声源。
|
| 图 7 测试样本Δf0和ΔQ分布图 |
设根据设置的阈值Tf0和TQ测得的故障次级声源数量为Ne, 则误报率η计算方法为
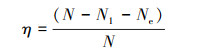
|
(25) |
由(25)式可得到不同Tf0和TQ阈值故障检测误报率(见表 8)。其中误报率η大于0表示故障数多报, 误报率η小于0表示故障数少报, 即故障检测阈值过大。
由表 8可知, 阈值Tf0如果设置小于10%会导致部分正常的次级声源被误判为发生了故障。阈值TQ如果设置小于10%, 也会导致部分正常的次级声源被误判为发生了故障, 设置大于11%时又存在少报, 即部分故障的次级声源被认为并没有发生故障。因此, 本次实验选用的次级声源最佳的Tf0阈值为10%~11%皆可, 而TQ阈值最佳为10%。
对100个次级声源样本的测试结果进行分析, 并结合样本Δf0和ΔQ值的变化, 由图 7可知, A区域的无故障次级声源, 部分在经过一定的工作时间后, 其特征值参数f0和Q也会发生一定变化, 从而接近故障状态, 这是由次级声源的工作原理和特性决定的, 自身工作发热或环境温度和湿度等变化都会导致次级声源的定心支片等部件发生性能改变。这也可作为判定次级声源产品质量性能的一个参考依据。B区域的故障多为次级声源的纸盆受到压迫, 振动减弱, 影响了对外的声辐射性能。C区域的故障为纸盆发生了破裂, 同时定心支片也受到了一定的损伤。D区域的故障为定心支片和纸盆受损严重, 通过听音明显感受到声音大小和频率成分的变化, 伴随有明显的“破音”。
3 结论为解决ANC系统中次级声源实时故障检测问题, 本文对次级声源故障检测系统原理、故障类型和检测方法进行理论分析, 给出了一种故障检测方法, 通过数值仿真和实验验证, 得到如下结论: ①通过次级声源的电压和电流信号, 根据其阻抗曲线, 获得特征值参数, 根据参数的变化可以准确判断出次级声源工作状态下的实时故障情况; ②该方法对次级声源故障检测无需针对不同的ANC使用场景测定标准值; ③故障检测的阈值可以根据经验值和降噪性能的要求来确定, 即次级声源的故障判定准则, 可以理解为次级声源性能的变化程度; ④次级声源工作时的阻抗曲线特征值变化可反映其性能稳定性及同批次产品性能的一致性。
| [1] | ELLIOTT S J, NELSON P A, et al. Active noise control[J]. Signal Processing Magazine, 1993, 10(4): 12-35. DOI:10.1109/79.248551 |
| [2] |
陈克安. 有源噪声控制[M]. 北京: 国防工业出版社, 2014.
CHEN Kean. Active noise control[M]. Beijing: Aotion Defence Indeustny Press, 2014. (in Chinese) |
| [3] | RAFAELY B, ELLIOTT S J, GARCIA-BONITO J. Broadband performance of an active headrest[J]. The Journal of Acoustic of Society of America, 1999, 106(2): 787-793. DOI:10.1121/1.427134 |
| [4] |
王磊, 陈克安, 胥健, 等. 应用卡尔曼滤波的有源头靠噪声控制策略[J]. 西北工业大学学报, 2021, 39(5): 937-944.
WANG Lei, CHEN Kean, XU Jian, et al. Noise control with Kalman filter for active headrest[J]. Journal of Northwestern Polytechnical University, 2021, 39(5): 937-944. (in Chinese) DOI:10.3969/j.issn.1000-2758.2021.05.001 |
| [5] |
李楠, 杨飞然, 杨军. 一种基于虚拟传感的无需误差传声器的自适应有源降噪方法[J]. 应用声学, 2019, 38(1): 85-92.
LI Nan, YANG Feiran, YANG Jun. An adaptive active noise method without an error microphone based on virtual microphone technique[J]. Journal of Applied Acoustics, 2019, 38(1): 85-92. (in Chinese) |
| [6] | DAVY M, DONCARLI C. A new nonstationary test procedure for improved loudspeaker fault detection[J]. Journal of the Audio Engineering Society, 2002, 50(6): 458-469. |
| [7] | WENHUA G, YUMING Q. A method of loudspeaker's pure tone fault detection based on time-frequency image fractal[J]. Recent Patents on Signal Processing, 2014, 4: 116-123. |
| [8] |
周静雷, 魏艳慧, 朱增友, 等. 基于矩形卷积窗的声频测量系统谐波分析方法[J]. 电声技术, 2011, 35(2): 71-74.
ZHOU Jinglei, WEI Yanhui, ZHU Zengyou, et al. Audio measurement system harmonic analysis based on retangular convolution window[J]. Audio Engineering, 2011, 35(2): 71-74. (in Chinese) |
| [9] | VALK R. Control of voicecoil transducers: design and implementation of a motional feedback loudspeaker woofer[D]. Delft: Delft University of Technology, 2013 |
| [10] | Venturi S, Panahi I. Hybrid RLS-NLMS algorithm for real-time remote active noise control using directional ultrasonic loudspeaker[C]//Conference of the IEEE Industrial Electronics Society, 2015 |
| [11] |
李云红, 李小英, 周静雷, 等. 掩蔽效应在扬声器异常音检测中的应用[J]. 西北大学学报, 2015, 45(2): 218-222.
LI Yunhong, LI Xiaoying, ZHOU Jinglei, et al. The application of masking effect in the speaker abnormal sounds detection[J]. Journal of Northwest University, 2015, 45(2): 218-222. (in Chinese) |
| [12] | SERBAN G, IANA G V, ANGHELESCU P. Fault detection of direct radiator loudspeaker systems by phase characterization[C]//8th International Conference on Electronics, 2016 |
| [13] | PHILIP L. Loudspeaker parameter identification for automatic fault detection[D]. Gothenburg: Chalmers University of Technology, 2018 |
2. Shaanxi Fenghuo Communication Group Co., Ltd, Baoji 721006, China;
3. School of Computer Science, Xi'an Shiyou University, Xi'an 710065, China




