在工程实际中, 由于生产水平、加工工艺等因素的制约, 结构系统的材料特性、结构尺寸和制造误差等变量中广泛地存在多种不确定性[1]。一般按照不确定性的来源可将其分为2类: 客观的不确定性和主观的不确定性。客观的不确定性与变量内在的固有随机性有关, 是不可缩减的固有属性, 而主观的不确定性与不完善的信息及有限的数据有关, 可随着认知的深入和数据的丰富而减小[2]。
灵敏度分析常常用来衡量模型输入不确定性对模型输出不确定性的贡献程度[3]。灵敏度分析分为局部灵敏度分析和全局灵敏度分析。其中, 全局灵敏度分析又被称为重要性测度分析, 用来衡量变量在其整个不确定性范围内变化时对输出性能统计特征的贡献程度[4]。目前国内外学者们对输入变量的重要性测度分析方法做了大量的研究, 比如Saltelli[5]提出了基于非参数的方法, Sobol[6]提出了基于方差的重要性分析方法, Borgonovo[7]提出了矩独立分析方法。由于基于方差的重要性测度分析方法具有模型独立、重要性测度与输入-输出关系一一对应等良好的特性, 是目前国际上最常使用的方法之一[8]。
上述提到的重要性测度分析方法并没有考虑输入变量分布参数的不确定性, 但实际上由于认知和测量水平的限制, 输入变量的分布参数并非是确切可知的, 因此分布参数具有不确定性的重要性分析方法得到了越来越多的关注[9]。分布参数的不确定性有多种描述方式, 常见的有区间模型[10]、模糊集模型[11]以及主观概率密度函数[12]等。对于存在分布参数不确定性的情况, 输入变量和分布参数的不确定性传递过程可定性地描述为: 分布参数→输入变量→输出变量→输出性能统计特征。因此分布参数的不确定性会引起输出性能统计特征的不确定性, 这就要求在进行重要性分析时考虑分布参数在其整个变化范围内对模型输出性能统计特征的影响。
对于分布参数具有不确定性的模型, 本文借助输入变量基于方差的重要性分析思想, 建立了衡量分布参数对输出统计矩影响的重要性测度指标, 并针对直接求解分布参数重要性测度指标需要3层蒙特卡洛(Monte Carlo, MC)抽样, 计算成本过高的问题, 提出2种基于代理抽样概率密度函数(surrogate sampling probability density function, SSPDF)[13]的求积公式(cubature formula, CF)方法来解决此问题。所提分析方法首先将求积公式运用到分布参数不确定性基于方差的重要性测度指标求解过程中, 以提高分布参数重要性测度指标中嵌套的期望和方差算子的计算效率; 其次, 引入代理抽样概率密度函数方法, 以降低输入变量参数不确定性向输出性能统计矩传递过程中的计算量; 最后, 将单层蒙特卡洛(quasi-Monte Carlo, QMC)方法[5]与求积公式相结合, 以降低重要性测度指标求解过程中嵌套的期望和方差算子的计算量。
1 分布参数基于方差的重要性测度指标当输入变量X的分布参数具有不确定性时, 输出的统计特征值也将具有不确定性。衡量输入变量的单个分布参数或多个分布参数的交互作用对模型输出统计特征值(这里以均值、方差为例)方差的贡献程度, 可以为改变分布参数以减小模型输出的不确定度提供依据[14]。
当输入变量X=(X1, X2, …, XdX)的分布参数Θ具有不确定性时, 模型输出将同时具有主观不确定和客观不确定, 可表示为
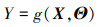
|
(1) |
式中, Θ=(Θ1, Θ2, …, ΘdΘ)是输入变量X的dΘ维相互独立的分布参数变量。在本文中, 参数的主观不确定性用主观概率密度函数fΘ(θ)来描述[12]。当Θ取某一特定值θ(·)时, 输入变量X的不确定性由条件概率密度函数fX(x|θ(·))来衡量。
当输入变量X的分布参数Θ具有不确定性时, 输出的均值和方差不再只受到输入变量X的不确定性影响, 而是可以描述为分布参数Θ的函数

|
(2) |
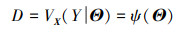
|
(3) |
因此, 类似于输入变量的基于方差的重要性测度的定义, 分布参数Θ分别对Μ和D的主重要性测度和总重要性测度如(4)~(5)式和(6)~(7)式所示
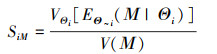
|
(4) |
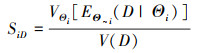
|
(5) |
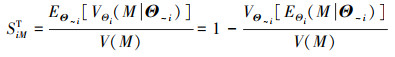
|
(6) |

|
(7) |
式中, Θ~i=(Θ1, …, Θi-1, Θi+1, …, ΘdΘ)是除了Θi以外的所有参数变量, 主重要性测度SiM和SiD分别表示参数变量Θi单独作用对输出均值Μ和方差D不确定性的贡献, 总重要性测度SiMT和SiDT分别表示参数变量Θi单独作用以及与其他所有参数变量的交互作用对M和D不确定性的总贡献[15]。
2 分布参数基于方差的重要性测度指标求解的高效方法从(4)~(7)式可以看出, 求解参数的重要性测度指标的关键仍在于求解嵌套的期望和方差算子。然而, 不同于输入变量基于方差的重要性测度指标, 参数的重要性测度指标求解过程需要将参数的不确定性传递到输出均值和方差, 是一个分布参数Θ和输入变量X嵌套的双层抽样过程。如果利用抽样方法求解(4)~(7)式中指标, 则整个过程是一个“3层嵌套”的抽样过程, 计算量太大难以为工程实际所接受[15]。求积公式利用少量的积分点和权重便能计算输出的均值和方差, 并且对更高维度的输入仍有良好的适用性与精确度[16]。Li等[13]提出的代理抽样概率密度函数方法可以将参数不确定性向输出均值和方差传递过程中的双层抽样简化为单层, 在很大程度上提高了参数不确定性传递的效率。因此, 本文将CF和SSPDF引入到参数的重要性分析中, 首先提出了参数重要性测度指标求解的S-DLCF算法, 然后再结合QMC方法, 提出了S-SLCF算法。
2.1 求积公式对于一个模型Z=φ(Θ)(Z可以是(2)式中的均值M或(3)式中的方差D), 由于CF估计统计矩是在标准正态空间中进行的[17], 因此首先通过Rosenblatt变换或Nataf变换将该模型转化为独立标准正态变量λ=(λ1, λ2, …, λdΘ)的一个函数[18]
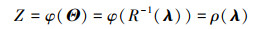
|
(8) |
式中,R-1(·)表示Rosenblatt变换或Nataf变换;ρ(λ)表示独立标准正态变量λ的多元函数。
因此, 根据(8)式, Z的一阶和二阶中心距, 也即Z的期望和方差, 可以表示为
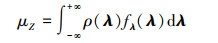
|
(9) |
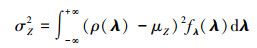
|
(10) |
式中, fλ(λ)表示独立标准正态变量λ的联合概率密度函数。
根据求积公式的理论, (9)~(10)式中的积分可利用少量合适的积分点和相应的积分权重高效地计算得出, 可以表示为[19]
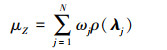
|
(11) |
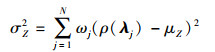
|
(12) |
式中, N是求积权重ωj与相应的积分点λj的数目。
Xu等[18]已经证明了CF能够精确估计大多数问题中函数的一阶矩和二阶矩。表 1~2中列出了目前已知的最有效的5类求积公式, 从其中可以看出, CF所需的积分点个数与变量维数有关且呈二次增长关系。
对于中低等维度变量, 积分点的个数只有几十个或几百个, 体现出了高效性[19]。公式Ⅰ、Ⅱ和Ⅴ受限于变量维度, 公式Ⅳ的计算误差随变量维数的增加而增加, 公式Ⅲ的计算误差相比较而言更加稳定[16]。
因此, 本文选择公式Ⅲ计算嵌套的期望和方差, 其表示形式为
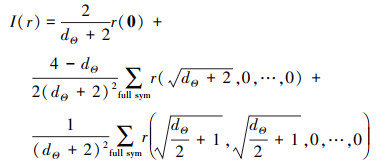
|
(13) |
式中:I(·)表示积分的简写;如果考虑(11)式中μZ及(12)式中σZ2, 则r(·)分别为ρ(λ)和(ρ(λ)-μZ)2。
2.2 代理抽样概率密度函数方法2.1节中的求积公式方法可以高效地求解(4)~(7)式中嵌套的期望和方差算子。然而, 在求解过程中首先需要将参数Θ的不确定性传递到输出的均值和方差, 该过程需要双层嵌套的输入变量X和参数Θ抽样。为解决计算成本昂贵的问题,Li等[13]提出了代理抽样概率密度函数方法。
考虑(8)式中的输出均值模型, 通过引入SSPDF hX(x|θ*), 可将输出均值M表示为
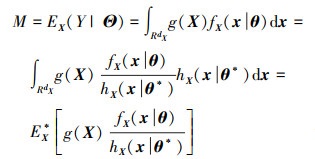
|
(14) |
式中,RdX为dX维输入变量的空间;fX(x|θ)为在分布参数条件下输入变量X的概率密度函数;EX*[·]表示关于代理抽样概率密度函数求均值。
根据方差的计算式V(Y)=E(Y2)-E2(Y), (9)式中的输出方差模型引入SSPDF hX(x|θ*)后, 可将输出方差D表示为

|
(15) |
由(14)~(15)式可知, 当在输出均值和方差函数的计算过程中引入SSPDF hX(x|θ*)时, 输入变量X是由含有确定参数θ*的SSPDF hX(x|θ*)产生, 不依赖于真实的分布参数。因此, 在计算M和D时, 分布参数Θ在外层变化, 内层所产生的输入变量X的样本可重复使用。
采用(14)~(15)式计算M和D时, SSPDF hX(x|θ*)的选取是关键。文献[13]指出, 当输入变量X随其具有不确定性的分布参数Θ改变时, hX(x|θ*)应该覆盖输入变量X的整个变化范围。一种简单而直接的方法是, 根据分布参数Θ的变化范围确定相应的输入变量X的极限分布, 然后根据输入变量X的极限分布确定SSPDF hX(x|θ*)。具体的选取方法可参考文献[13]。
2.3 基于代理抽样概率密度函数的双层求积公式(S-DLCF)算法将(2)~(3)式中的输出期望和方差模型统一表示为2.1节提到的Z=φ(Θ), 参数Θ的不确定性可以通过2.2节的代理抽样概率密度方法传递到输出Z。从(4)~(7)式可以看出, 求解重要性测度指标的关键是计算分布参数对Z方差的贡献VΘi[EΘ~i(Z|Θi)]和VΘ~i[EΘi(Z|Θ~i)], 而这些方差贡献均是期望和方差算子的嵌套。由于该算法的双层嵌套过程较长, 将其分为两部分进行描述。
首先, 求解SiZ, 也即通过S-DLCF求解分布参数Θi对Z的主重要性测度, 其基本步骤如下所示[19]
1) 估计无条件期望E(Z)和方差V(Z)
① 根据求积公式Ⅲ产生dΘ维分布参数的积分点ξldΘ (l=1, …, NΘdΘ)和相应的权重ωl(l=1, …, NΘdΘ)。通过Rosenblatt变换或Nataf变换将ξldΘ(l=1, …, NΘdΘ)变换到原模型空间得到θldΘ(l=1, …, NΘdΘ)。
② 根据2.2节方法确定SSPDF hX(x|θ*), 并由hX(x|θ*)抽取输入变量X的NX个样本xk(k=1, …, NX), 进而求得相应的模型输出Y。
③ 根据hX(x|θ*), fX(x|θ)和Y=g(x)的样本hX(xk|θ*)(k=1, …, NX), fX(xk|θ)(k=1, …, NX)和Y=g(xk)(k=1, …, NX)以及Θ的积分点θldΘ (l=1, …, NΘdΘ), 利用(14)式或(15)式求解得到Z的积分点zl(l=1, …, NΘdΘ)。
④ 由zl(l=1, …, NΘdΘ)和ωl(l=1, …, NΘdΘ)利用(13)式求解Z的期望E(Z)和方差V(Z)。
2) 估计EΘ~i(Z|Θi)和VΘi[EΘ~i(Z|Θi)]
① 根据求积公式Ⅲ产生一维分布参数的积分点ξl1 (l=1, …, NΘ1)和相应的权重ωl(l=1, …, NΘ1)。通过Rosenblatt变换或Nataf变换将ξl1 (l=1, …, NΘ1)变换到原模型空间得到θl1 (l=1, …, NΘ1)。
② 当参数Θi=θl1(l=1, …, NΘ1)时, 根据2.2节方法确定新的SSPDF hX(x|θ~i*, θl1), 并由hX(x|θ~i*, θl1)抽取输入变量X的NX个样本x ′ k(k=1, …, NX), 进而求得相应的模型输出Y′。
③ 根据求积公式Ⅲ产生dΘ-1维分布参数的积分点ξldΘ-1(l=1, …, NΘdΘ-1)和相应的权重ωl(l=1, …, NΘdΘ-1)。通过Rosenblatt变换或Nataf变换将ξldΘ-1 (l=1, …, NΘdΘ-1)变换到原模型空间得到θldΘ-1(l=1, …, NΘdΘ-1)。
④ 根据hX(x|θ~i*, θl1), fX(x|θ~i, θl1)和Y=g(x)的样本hX(x ′ k|θ~i*, θl1)(k=1, …, NX), fX(x ′ k|θ~i, θl1)(k=1, …, NX)和Y′=g(x ′ k)(k=1, …, NX)以及Θ~i的积分点θldΘ-1(l=1, …, NΘdΘ-1), 利用(14)或(15)式求解zl(l=1, …, NΘdΘ-1)。
⑤ 由zl(l=1, …, NΘdΘ-1)和ωl(l=1, …, NΘdΘ-1)利用(13)式求解Z的条件期望EΘ~i(Z|Θi=θl1)(l=1, …, NΘ1)。
⑥ 条件期望EΘ~i(Z|Θi=θl1)(l=1, …, NΘ1)可以看作是单变量Θi的函数, 由EΘ~i(Z|Θi=θl1)(l=1, …, NΘ1)和ωl(l=1, …, NΘ1)利用(19)式求解EΘi[EΘ~i(Z|Θi)]和VΘi[EΘ~i(Z|Θi)]。
3) 将求得的V(Z)和VΘi[EΘ~i(Z|Θi)]代入(4)或(5)式中便可得到SiZ。
类似地, 求解SiZT, 其基本步骤如下所示[19]。
1) 和求解主重要性测度时的步骤1)相同。
2) 估计VΘi(Z|Θ~i)和EΘ~i[VΘi(Z|Θ~i)]
① 根据求积公式Ⅲ产生dΘ-1维分布参数的积分点ξldΘ-1(l=1, …, NΘdΘ-1)和相应的权重ωl(l=1, …, NΘdΘ-1)。将ξldΘ-1(l=1, …, NΘdΘ-1)变换到原模型空间得到θldΘ-1(l=1, …, NΘdΘ-1)。
② 当参数Θi~=θldΘ-1(l=1, …, NΘdΘ-1)时, 根据2.2节方法确定新的SSPDF hX(x θi*, θldΘ-1), 并由hX(x θi*, θldΘ-1)抽取输入变量X的NX个样本x ′ k(k=1, …, NX), 进而求得相应的模型输出Y′。
③ 根据求积公式Ⅲ产生一维分布参数的积分点ξl1(l=1, …, NΘ1)和相应的权重ωl(l=1, …, NΘ1)。将ξl1(l=1, …, NΘ1)变换到原模型空间得到θl1(l=1, …, NΘ1)。
④ 根据hX(x θi*, θldΘ-1), fX(x θi, θldΘ-1)和Y=g(x)的样本hX(x ′ k|θi*, θldΘ-1)(k=1, …, NX), fX(x ′ k|θi, θldΘ-1)(k=1, …, NX)和Y′=g(x ′ k)(k=1, …, NX)以及Θi的积分点θl1(l=1, …, NΘ1), 利用(14)或(15)式求解Z的积分点zl(l=1, …, NΘ1)。
⑤ 由zl(l=1, …, NΘ1)和ωl(l=1, …, NΘ1)利用(13)式求解Z的条件期望EΘi(Z|Θ~i=θldΘ-1)(l=1, …, NΘdΘ-1)和条件方差VΘi(Z|Θ~i=θldΘ-1)(l=1, …, NΘdΘ-1)。
⑥ 由VΘi(Z|Θ~i=θldΘ-1)(l=1, …, NΘdΘ-1)和ωl(l=1, …, NΘdΘ-1)利用(13)式求解EΘ~i[VΘi(Z|Θ~i)]。
3) 将求得的V(Z)和EΘ~i[VΘi(Z|Θ~i)]代入(6)或(7)式便可得到SiZT。
2.4 基于代理抽样概率密度函数的单层求积公式(S-SLCF)算法该算法将QMC方法[5]的思想引入到求解嵌套的期望与方差中。对于模型Z=φ(Θ), 以方差贡献VΘi[EΘ~i(Z|Θi)]和VΘ~i[EΘi(Z|Θ~i)]为例, 准蒙特卡洛法求解嵌套期望和方差可表示为
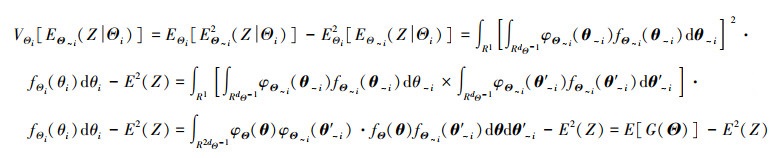
|
(16) |
式中, θ~i和θ ′ ~i是由条件概率密度函数fΘ~i(θ~i)产生的2组不同的条件样本点, G(Θ)=φΘ(θ)φΘ~i(θ ′ ~i)。对于(16)式中模型Z=φ(Θ)的条件输出的求解仍可利用(14)或(15)式的代理抽样概率密度函数方法。
根据(16)式, 通过将积分维度从dΘ维扩展到2dΘ-1维, 可将(10)式或(11)式中的双层嵌套积分简化为单层积分, 只需要分别估计期望E[G(Θ)]和无条件期望E(Z)便可得到VΘi[EΘ~i(Z|Θi)], 进而可得主重要性测度, 这大大简化了求解过程。
同样地, 求解VΘ~i[EΘi(Z|Θ~i)]可被简化为

|
(17) |
式中,G′(Θ)=φΘ(Θ)φΘi(Θ′ i)。利用(17)式求解VΘ~i[EΘi(Z|Θ~i)], 关键是分别求解dΘ+1维函数G′(Θ)的期望E[G′(Θ)]。
利用S-SLCF方法求解分布参数Θi对Z的主重要性测度和总重要性测度的基本步骤为:
1) 根据求积公式Ⅲ产生2dΘ维分布参数的积分点ξl2dΘ(l=1, …, NΘ2dΘ)和相应的权重ωl(l=1, …, NΘ2dΘ)。将ξl2dΘ(l=1, …, NΘ2dΘ)分解为三部分: 前(1~dΘ)维记为ξldΘ(l=1, …, NΘ2dΘ), 第(dΘ+1~2dΘ-1)维记为ξldΘ-1(l=1, …, NΘ2dΘ), 第2dΘ维记为ξl1(l=1, …, NΘ2dΘ)。
2) 将ξldΘ(l=1, …, NΘ2dΘ), ξldΘ-1(l=1, …, NΘ2dΘ)和ξl1(l=1, …, NΘ2dΘ)分别变换到原模型空间得到θldΘ(l=1, …, NΘ2dΘ), θldΘ-1(l=1, …, NΘ2dΘ)和θl1(l=1, …, NΘ2dΘ), 并将θldΘ表示为(θi, ldΘ, θ~i, ldΘ)。
3) 根据2.2节确定相应的SSPDF hX(x|θ*), 用hX(x|θ*)抽取输入变量X的NX个样本xk(k=1, …, NX), 进而求得相应的模型输出Y。
4) 根据hX(x|θ*), fX(x θ)和Y=g(x)的样本hX(xk|θ*)(k=1, …, NX), fX(xk|θ)(k=1, …, NX), Y=g(xk)(k=1, …, NX)和Θ的积分点θldΘ(l=1, …, NΘ2dΘ), 利用(14)式或(15)式求解Z的积分点zl(l=1, …, NΘ2dΘ)。
5) 由zl(l=1, …, NΘ2dΘ)和权重ωl(l=1, …, NΘ2dΘ)利用(13)式求解Z的期望E(Z)和方差V(Z)。
6) 当Θ=(θldΘ-1, θi, ldΘ)(l=1, …, NΘ2dΘ)时, 根据样本hX(xk|θ*)(k=1, …, NX), fX(xk|θldΘ-1, θi, ldΘ)(k=1, …, NX), Y=g(xk)(k=1, …, NX)和积分点(θldΘ-1, θi, ldΘ)(l=1, …, NΘ2dΘ), 利用(14)或(15)式求解z′ ~i, l(l=1, …, NΘ2dΘ)。
7) 由zl(l=1, …, NΘ2dΘ)和z′ ~i, l(l=1, …, NΘ2dΘ)以及相应的权重ωl(l=1, …, NΘ2dΘ), 利用(13)式求解函数G(Θ)=φ(θ)φΘ~i(θ ′ ~i)的期望E[G(Θ)]。
8) 将E[G(Θ)]和E(Z)代入到式(16)中得到VΘi[EΘ~i(Z|Θi)], 将该结果及步骤5)中求得的V(Z)代入到(4)式或(5)式中得到SiZ。
9) 当Θ=(θl1, θ~i, ldΘ)(l=1, …, NΘ2dΘ)时, 根据样本hX(xk|θ*)(k=1, …, NX), fX(xk|θl1, θ~i, ldΘ)(k=1, …, NX)和Y=g(xk)(k=1, …, NX)以及积分点(θl1, θ~i, ldΘ)(l=1, …, NΘ2dΘ), 利用(14)或(15)式求解z′ i, l(l=1, …, NΘ2dΘ)。
10) 由zl(l=1, …, NΘ2dΘ)和z′ i, l(l=1, …, NΘ2dΘ)以及相应的权重ωl(l=1, …, NΘ2dΘ), 利用(13)式求解函数G′(Θ)=φ(θ)φΘi(θ′ i)的期望E[G′(Θ)]。
11) 将E[G′(Θ)]和E(Z)代入到(17)式中得到VΘ~i[EΘi(Z|Θ~i)], 将结果及步骤5)中求得的V(Z)代入到(6)或(7)式中得到SiZT。
2.5 2种算法的比较将2.3节和2.4节对比来看, 2种新方法都利用了求积公式求解积分时的高效性和准确性, S-SLCF比S-DLCF更加简洁明了, 这是因为S-DLCF分两部分求解主和总重要性测度, 而S-SLCF只需要单层抽样便可求得这2个指标。另外, 在求解SiZ和SiZT时, S-DLCF和S-SLCF所需要调用功能函数的次数分别为(NΘ1+NΘdΘ-1)×dΘ×NX+NX和NX。
3 算例分析在本节的算例计算过程中, 为了验证所提方法的效率和精度, 以MC方法所得结果作为参考解[20], 以QMC方法所得结果作为对比解。在求解分布参数的主重要性测度指标和总重要性测度指标时, MC方法的模型调用次数为dΘ×NΘ×NΘ×NX, QMC方法的模型调用次数为(dΘ+2)×NΘ×NX, 其中MC方法中的样本量统一为NX=NΘ=2 500, QMC方法中的样本量统一为NX=NΘ=30 000, 以保证所求的重要性测度指标收敛。
3.1 可加性非线性模型考虑非线性程度较小的功能函数g(X)=40-18X1+X22+X2+X32+5X3。其中输入变量X1, X2和X3相互独立且服从同一均值为μ, 标准差为1的正态分布, 同时分布参数具有不确定性且服从正态分布, 即μi~N(4, 12)(i=1, 2, 3)。
根据SSPDF的选取原则, 该算例中选取SSPDF为正态分布N(4, 22)来抽取输入变量X的样本。
2种所提方法计算得到的重要性测度指标如表 3所示, eQMC, eS-DLCF, eS-SLCF分别表示各方法相对于MC方法得到的参考解的相对误差。其中,4种方法的计算量分别为3×(2 500)3, 5×(30 000)2, 37×1 000, 5 000。
| 重要性指标 | MC | QMC | eQMC/% | S-DLCF | eS-DLCF/% | S-SLCF | eS-SLCF/% | |
| SiM | μ1 | 0.564 78 | 0.555 97 | 1.56 | 0.564 70 | 0.01 | 0.564 31 | 0.08 |
| μ2 | 0.140 33 | 0.138 80 | 1.09 | 0.139 50 | 0.59 | 0.141 70 | 0.98 | |
| μ3 | 0.289 78 | 0.288 22 | 0.54 | 0.288 80 | 0.34 | 0.291 40 | 0.56 | |
| STiM | μ1 | 0.562 39 | 0.562 52 | 0.02 | 0.564 08 | 0.30 | 0.562 05 | 0.06 |
| μ2 | 0.140 19 | 0.140 71 | 0.37 | 0.141 34 | 0.82 | 0.140 56 | 0.26 | |
| μ3 | 0.286 15 | 0.278 75 | 2.59 | 0.285 11 | 0.36 | 0.291 40 | 1.83 | |
| SiD | μ1 | 0.003 70 | 0.005 28 | 42.58 | 0.003 68 | 0.64 | 0.004 02 | 8.37 |
| μ2 | 0.305 42 | 0.305 32 | 0.03 | 0.304 03 | 0.45 | 0.309 11 | 1.21 | |
| μ3 | 0.642 13 | 0.641 64 | 0.08 | 0.642 20 | 0.01 | 0.641 69 | 0.07 | |
| SiDT | μ1 | 0.053 31 | 0.054 44 | 2.11 | 0.052 28 | 1.93 | 0.052 64 | 1.26 |
| μ2 | 0.373 15 | 0.384 33 | 3.00 | 0.377 33 | 1.12 | 0.372 86 | 0.08 | |
| μ3 | 0.675 23 | 0.683 41 | 1.21 | 0.679 97 | 0.70 | 0.679 52 | 0.64 |
从表 3中可以看出, 本文2种方法都在很大程度上提高了重要性分析的计算效率, 并且计算结果与参考解吻合良好。相比于QMC方法, 所提方法不但提高了计算效率, 并且具有更高的计算精度。根据参数对输出均值的重要性测度指标SiM和SiMT, 各分布参数的重要性排序均为μ1>μ3>μ2, 这表明在控制输出均值的稳定性时, 应该注重对分布参数μ1的主观信息收集; 根据参数对输出方差的重要性测度指标SiD和SiDT, 分布参数μ3对输出方差的影响均为最大, μ2次之, μ1最小, 这表明在实际过程中, 通过对分布参数μ3的主观信息收集能够最大程度地减小输出方差的变异性。
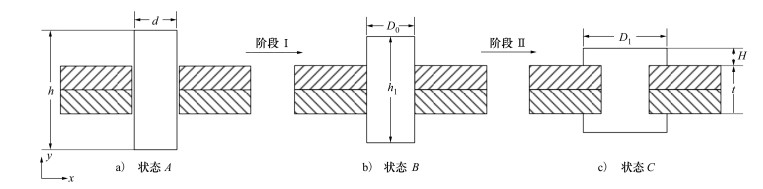
3.2 铆接结构在航空工业中, 真实的铆接过程非常复杂, 本文以无头铆钉为例, 将铆接过程简化为如图 1所示的2个阶段。第Ⅰ阶段中, 铆钉从状态A(冲击前的初始状态, 无变形)到状态B(中间状态, 铆钉和孔隙之间无缝隙)。第Ⅱ阶段中, 铆钉从状态B到状态C(铆钉受冲击后的最终状态, 头部被加工成型)。
|
| 图 1 简化的无头铆钉铆接过程 |
为了建立铆接过程中的铆钉挤压应力与几何尺寸之间的数学关系, 可以假设以下几个理想条件:
1) 铆接过程中铆钉孔直径不变
2) 铆钉体积的改变忽略不计
3) 铆接过程结束后, 铆钉的受力面为圆柱面
4) 铆钉材料具有各向同性
铆接前, 图 1a)中的状态A下铆钉的初始体积V0可以由(18)式表示
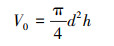
|
(18) |
式中, d和h分别表示状态A下铆钉的直径和长度。
第Ⅰ阶段后, 状态B下铆钉的体积可由(19)式表示为

|
(19) |
式中, D0和h1分别表示状态B下铆钉的直径和长度。
第Ⅱ阶段后, 假设铆钉在状态C下的上下表面的尺寸相同, 则状态C下铆钉的体积可由(20)式表示为

|
(20) |
式中:t为薄壁件的整体厚度;D1和H分别表示状态C下铆钉头的直径和长度。
根据硬化强度理论, y方向上的最大挤压应力σmax可以由(21)式表示为
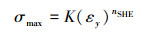
|
(21) |
式中:K为强度系数;nSHE为铆钉材料的硬化因子;εy为铆钉头在铆接过程中y方向上的真实应变。真实应变εy由第Ⅰ阶段中产生的应变εy1和第Ⅱ阶段中产生的应变εy2组成, 因此, εy可由(22)式表示为
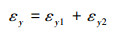
|
(22) |
式中: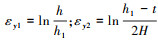
已经假设铆钉在铆接过程中体积不变, 由(18)~(22)式可得铆钉的最大挤压应力可以由(23)式表示为

|
(23) |
本文选取的铆钉材料为2017-T4, 其硬化指数nSHE=0.15。为保证铆钉上下端有一定的余量, 假设铆钉头高度H=2.2 mm。根据材料手册, 铆钉的挤压强度为σsq=565 MPa, 如果最大挤压应力大于挤压强度, 铆钉就可能会失效, 因此可以建立极限状态方程如(24)式所示
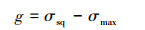
|
(24) |
在整个铆接过程中, 假设各随机变量之间相互独立且服从表 4所示的正态分布, 其均值存在主观不确定性且服从表 5所示的正态分布。
| 输入变量 | 均值 | 标准差 |
| d/mm | μd | 0.5 |
| h/mm | μh | 2 |
| D0/mm | μD0 | 0.051 |
| t/mm | μt | 0.05 |
| K/MPa | μK | 10.944 |
根据选取原则, 该算例中输入变量d, h, D0, t和K的SSPDF分别为N(5, 0.62), N(20, 2.52), N(5.1, 0.1022), N(5, 0.12)和N(547.2, 16.4162)。
表 6展示了4种方法得到的重要性测度指标以及每种方法所需调用功能函数的次数, 从中可以得出, 4种方法的计算量分别为5×(2 500)3, 7×(30 000)2, 181×10 000, 18 000。从表中可以看出,相比于MC方法和QMC方法, S-DLCF方法和S-SLCF方法在满足计算精度的前提下, 2种新方法都能有效降低分布参数重要性分析过程中的计算量, 并且S-SLCF方法比S-DLCF方法的计算量更少, 表现了S-SLCF方法在重要性测度指标求解过程中更高的计算效率。
| 重要性指标 | MC | QMC | eQMC/% | S-DLCF | eS-DLCF/% | S-SLCF | eS-SLCF/% | |
| SiM | μd | 0.039 46 | 0.038 61 | 2.16 | 0.039 11 | 0.90 | 0.039 44 | 0.04 |
| μh | 0.169 30 | 0.169 67 | 0.22 | 0.169 19 | 0.07 | 0.170 26 | 0.57 | |
| μD0 | 0.008 66 | 0.006 23 | 28.08 | 0.008 64 | 0.19 | 0.008 58 | 0.92 | |
| μt | 0.002 17 | 0.001 25 | 42.26 | 0.002 17 | 0.06 | 0.002 10 | 3.21 | |
| μK | 0.776 59 | 0.775 43 | 0.15 | 0.775 12 | 0.19 | 0.777 27 | 0.09 | |
| SiMT | μd | 0.043 58 | 0.043 18 | 0.92 | 0.043 21 | 0.86 | 0.043 51 | 0.16 |
| μh | 0.184 77 | 0.188 15 | 1.83 | 0.184 03 | 0.40 | 0.183 08 | 0.92 | |
| μD0 | 0.019 90 | 0.014 21 | 28.59 | 0.018 96 | 4.71 | 0.019 34 | 2.79 | |
| μt | 0.014 57 | 0.014 31 | 1.79 | 0.014 17 | 2.75 | 0.014 26 | 2.18 | |
| μK | 0.783 46 | 0.785 23 | 0.23 | 0.781 32 | 0.27 | 0.783 26 | 0.02 | |
| SiD | μd | 0.295 94 | 0.291 01 | 1.67 | 0.303 34 | 2.50 | 0.291 42 | 1.53 |
| μh | 0.407 56 | 0.398 71 | 2.17 | 0.403 82 | 0.92 | 0.412 94 | 1.32 | |
| μD0 | 0.044 76 | 0.046 52 | 3.93 | 0.044 52 | 0.53 | 0.043 02 | 3.88 | |
| μt | 0.011 64 | 0.011 48 | 1.42 | 0.011 65 | 0.02 | 0.011 62 | 0.20 | |
| μK | 0.006 80 | 0.011 13 | 63.69 | 0.006 91 | 1.68 | 0.006 65 | 2.24 | |
| SiDT | μd | 0.489 39 | 0.497 67 | 1.69 | 0.496 94 | 1.54 | 0.497 29 | 1.61 |
| μh | 0.571 98 | 0.567 66 | 0.76 | 0.577 24 | 0.92 | 0.567 76 | 0.74 | |
| μD0 | 0.134 44 | 0.136 55 | 1.57 | 0.136 59 | 1.60 | 0.133 97 | 0.34 | |
| μt | 0.083 36 | 0.079 19 | 5.01 | 0.082 16 | 1.44 | 0.082 65 | 0.85 | |
| μK | 0.064 37 | 0.066 49 | 3.29 | 0.062 63 | 2.70 | 0.065 65 | 1.98 |
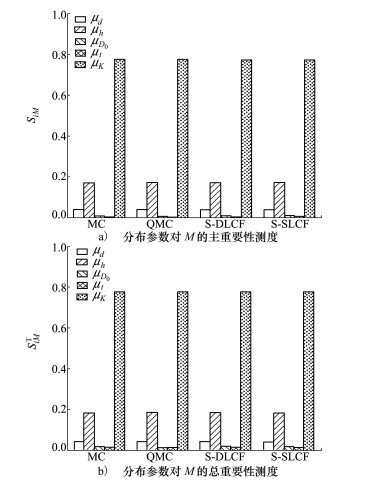
从图 2~3可以得出, 各分布参数不确定性的2个重要性测度指标SiM和SiMT的大小近似相同, 这说明各分布参数分别与其他参数的交互作用对输出均值的影响可以忽略不计。各分布参数的重要性测度排序为: μK>μh>μd>μD0>μt, 因此要最大程度地提高结构系统输出均值的稳定性, 需对参数μK进行有效调节; 分布参数不确定性的2个重要性测度指标SiD和SiDT的大小不同而其趋势近似相同, 这说明分布参数之间的交互作用对输出方差有一定的影响。各分布参数的重要性排序为: μh>μd>μD0>μt>μK, 因此, 需要增加对分布参数μh, μd的不确定性的关注度以降低输出方差的变异性。此外, 分布参数对输出均值和方差的2种重要性测度指标的排序并不相同, 这说明影响输出不同特征的主要参数一般是不同的, 在实际工程中需要根据所关心的输出特征有针对性地选择合适的重要性测度指标。
|
| 图 2 算例3.2在不同方法下计算得出的输出均值重要性测度对比图 |

|
| 图 3 算例3.2在不同方法下计算得出的输出方差重要性测度对比图 |
本文研究了分布参数具有不确定性时的重要性分析问题, 首先定义了衡量分布参数不确定性对输出均值和方差影响的重要性测度指标。其次, 针对传统MC方法在进行参数重要性分析时计算量大、工程难以接受的缺点, 以求积公式为基础, 结合SSPDF, 提出了参数不确定性重要性测度求解的两种新算法, 大大降低了参数不确定性重要性分析的成本。
所提新算法的效率和精度取决于两方面: 一方面是CF的选择, 另一方面是SSPDF的选取。对于CF的选择, 依赖于问题的维数, 本文选择的是求积公式Ⅲ, 该公式在求解低等到中等维度的问题时有较好的精度及效率; 对于SSPDF的选取, 一个合适的SSPDF应该覆盖分布参数确定的输入变量的整个变化范围, 本文采用了与原输入变量具有相同分布的方法确定SSPDF。
通过数值算例和工程算例的分析结果可以得出, 所提的新算法在求解主重要性测度和总重要性测度时都体现出了较高的精度, 并能准确对分布参数的重要性进行排序。与QMC方法比较, 2种新算法在大幅度减少计算量的同时表现出了更优的计算精度; 而S-DLCF与S-SLCF相比, S-DLCF所得结果的相对误差更小, 计算结果更有效; 而S-SLCF通过引入准蒙特卡洛法, 真正意义上将求解分布参数不确定性下的重要性测度指标时的3层MC抽样方法简化为单层抽样, 计算过程更加简洁。在工程实际中, 可以根据具体的问题选择不同的算法。
| [1] | YUN W Y, LU Z Z, HE P F, et al. An efficient method for estimating the parameter global reliability sensitivity analysis by innovative single-loop process and embedded Kriging model[J]. Mechanical Systems and Signal Processing, 2019, 133: 106288. DOI:10.1016/j.ymssp.2019.106288 |
| [2] | GUO J, DU X P. Sensitivity analysis with mixture of epistemic and aleatory uncertainties[J]. AIAA Journal, 2007, 45(9): 2337-2349. DOI:10.2514/1.28707 |
| [3] | TORⅡ A J, NOVOTNY A A. A priori error estimates for local reliability-based sensitivity analysis with Monte Carlo simulation[J]. Reliability Engineering & System Safety, 2021, 213(3): 107749. |
| [4] | LI L Y, LU Z Z. Regional importance effect analysis of the input variables on failure probability[J]. Computers & Structures, 2013, 125: 74-85. |
| [5] | SALTELLI A. Sensitivity analysis for importance assessment[J]. Risk Analysis, 2002, 22(3): 579-590. DOI:10.1111/0272-4332.00040 |
| [6] | SOBOL I M. Sensitivity estimates for nonlinear mathematical models[J]. Mathematical and Computer Modelling, 1993, 1(4): 407-414. |
| [7] | BORGONOVO E. A new uncertainty importance measure[J]. Reliability Engineering & System Safety, 2007, 92(6): 771-784. |
| [8] | HAO W R, LU Z Z, LI L Y. A new interpretation and validation of variance based importance measures for models with correlated inputs[J]. Computer Physics Communications, 2013, 184(5): 1401-1413. DOI:10.1016/j.cpc.2013.01.007 |
| [9] |
锁斌, 曾超, 程永生, 等. 认知不确定性下可靠性灵敏度分析的新指标[J]. 航空学报, 2013, 34(7): 1605-1615.
SUO Bin, ZENG Chao, CHENG Yongsheng, et al. New index for reliability sensitivity analysis under epistemic uncertainty[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(7): 1605-1615. (in Chinese) |
| [10] | WANG L, XIONG C, WANG X, et al. A dimension-wise method and its improvement for multidisciplinary interval uncertainty analysis[J]. Applied Mathematical Modelling, 2018, 59: 680-695. DOI:10.1016/j.apm.2018.02.022 |
| [11] | PEREZ-CANEDO B, CONCEPCION-MORALES E R. A method to find the unique optimal fuzzy value of fully fuzzy linear programming problems with inequality constraints having unrestricted L-R fuzzy parameters and decision variables[J]. Expert Systems with Applications, 2019, 123: 256-269. DOI:10.1016/j.eswa.2019.01.041 |
| [12] | SANKARARAMAN S, MAHADEVAN S. Separating the contributions of variability and parameter uncertainty in probability distributions[J]. Reliability Engineering & System Safety, 2013, 112: 187-199. |
| [13] | LI L Y, LU Z Z. A new algorithm for importance analysis of the inputs with distribution parameter uncertainty[J]. International Journal of Systems Science, 2016, 47(13): 3065-3077. DOI:10.1080/00207721.2015.1088099 |
| [14] | LI L Y, LU Z Z, FENG J, et al. Moment-independent importance measure of basic variable and its state dependent parameter solution[J]. Structural Safety, 2012, 38: 40-47. DOI:10.1016/j.strusafe.2012.04.001 |
| [15] | WANG P, LU Z Z, TANG Z C. An application of the Kriging method in global sensitivity analysis with parameter uncertainty[J]. Applied Mathematical Modelling, 2013, 37(9): 6543-6555. DOI:10.1016/j.apm.2013.01.019 |
| [16] | LU J, DARMOFAL D L. Higher-dimensional integration with Gaussian weight for applications in probabilistic design[J]. Siam Journal on Scientific Computing, 2004, 26(2): 613-624. |
| [17] | HUANG X Z, LI Y X, ZHANG Y M, et al. A new direct second-order reliability analysis method[J]. Applied Mathematical Modelling, 2018, 55: 68-80. |
| [18] | XU J, LU Z H. Evaluation of moments of performance functions based on efficient cubature formulation[J]. Journal of Engineering Mechanics, 2017, 143(8): 06017007. |
| [19] | LIU Y S, LI L Y, ZHOU C C, et al. Efficient multivariate sensitivity analysis for dynamic models based on cubature formula[J]. Engineering Structures, 2020, 206: 110164. |
| [20] | ZHANG X B, LU Z H, CHENG K, et al. A novel reliability sensitivity analysis method based on directional sampling and Monte Carlo simulation[J]. Journal of Risk and Reliability, 2020, 234(4): 622-635. |




