2. 西安现代控制技术研究所, 陕西 西安 710065;
3. 西北工业大学 航天学院, 陕西 西安 710072
关联分析是发现、查询数据之间关联性或相关性的一种实用分析技术,描述了事物中某些属性同时出现的规律和模式[1-2]。关联分析在经济学、军事学、互联网、航空航天及人工智能等领域有着广泛应用[3-4],其中时间序列分析是数据关联分析领域的热点研究内容。
对不同工程背景及应用需求,目前已经提出了多种数据关联分析方法[5-6]。文献[1]提出了一种信息不确定条件下的时间序列关联分析法,解决了时间序列中含有不确定信息时的数据关联分析问题。文献[7]提出了一种灰色关联分析方法,解决了时间序列曲线相似性关联分析问题。常见的时间序列关联分析方法还有TIC法、相关系数法、误差分析法、EARTH方法等[7],这些方法操作简单,应用广泛,但主要适用于单样本时间序列之间的分析,不适合工程中经常遇到的多样本(多元)时间序列情况[4]。针对多样本关联分析,文献[4]提出了一种概率关联度模型和概率关联分析方法,实现了由序列曲线关联向立体面板关联的方法拓展,但计算时需要由比较序列样本构建累积分布函数。实际应用中由于试验抽样的昂贵性、复杂性和困难性等,比较序列在实际情况中常常是小样本数据容量,构建的累积分布函数与真实分布差别一般较大,若直接应用概率关联度模型,关联分析效果较差,严重影响了概率关联度模型的工程应用范围。
针对上述问题,本文提出一种小样本概率关联度模型。使用样本函数或样本统计量代替样本构造累积经验分布函数并计算概率关联系数,发展了概率关联度模型的理论框架。当比较序列样本容量n < 5时,使用样本函数或样本统计量构建累积分布函数计算概率关联系数;当比较序列样本容量n≥5时,使用Bootstrap方法重抽样扩展样本后构建积累分布函数计算概率关联系数,改进了概率关联度模型中关联系数的计算方法,从而提高了概率关联分析的效率。通过仿真案例和实际应用验证了本文方法的正确性和有效性。
1 问题描述与分析假设有参考序列x为
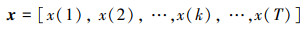
|
(1) |
比较序列y为
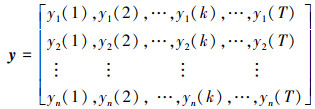
|
(2) |
式中: k为时刻; T为序列长度。
参考序列x和比较序列y之间的数据关联度为C, 一般地, C可由如(3)式计算
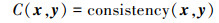
|
(3) |
式中: consistency(·)为一致性分析函数, 也称一致性检验算子, 一般有C(x, y)∈[0, 1]。文献[4]总结分析了目前常见的一致性分析函数consistency(·), 并提出了一种适合多样本时间序列的概率关联算子和概率关联分析方法。
参考序列x和比较序列y之间的概率关联度计算步骤如下[4]:
步骤1 计算k时刻概率关联系数poperator(k)

|
(4) |
步骤2 计算概率关联度p
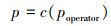
|
(5) |
式中: Fy(k)(·)为由比较序列样本y1∶n(k)确定的累积分布函数; Fy(k)(x(k))为x(k)在累积分布函数Fy(k)中的累积分布函数值; c(·)为概率关联度模型中的综合概率度计算公式, 可取均匀检验结果。
从(4)~(5)式可见, 步骤1中需要由比较序列样本y1∶n(k)构建累积分布函数Fy(k), 当比较序列y1∶n(k)样本容量较大时(样本量n较大时), 可以构建比较精确的累积分布函数Fy(k), 综合计算得到的概率关联度p比较符合实际。当比较序列y1∶n(k)样本容量较小时, 由比较序列y1∶n(k)构建的累积分布函数Fy(k)因抽样误差与实际分布函数差距较大, 此时, 若应用综合计算概率关联度p进行分析决策风险较大。工程实际中, 由于试验抽样的昂贵性、复杂性和困难性, 经常会遇到小样本情况的比较序列数据, 限制了概率关联度模型的实际应用效果和应用范围。
2 小样本概率关联度模型 2.1 改进思路综上可知, 小样本条件下概率关联度模型应用遇到的主要问题是: 比较序列y1∶n(k)样本容量n有限, 基于比较序列样本y1∶n(k)不容易构建精确的累积分布函数Fy(k), 导致概率关联度模型使用效果较差。解决该问题的有效方法是使用小样本比较序列y1∶n(k)构建满足要求的累积分布函数Fy(k)。
Bootstrap方法是Efron于1979年提出的一种逼近复杂系统统计量估计值分布的统计方法[8], 是目前被广泛采用的小样本数据处理方法, 可以用来解决概率关联度模型面临的小样本问题, 即使用Bootstrap方法重抽样扩展样本后构建积累分布函数计算概率关联系数。但通常Bootstrap方法样本容量以n≥5较合适[9-10], 当n < 5时, 其计算结果的任意性很大, 构造的经验分布函数和统计效果较差。针对样本容量n < 5的情况, 文献[3, 9]使用了一种样本顺序比率统计量K, 在样本容量n < 5的条件下应用效果较好[3], 认为相对于样本总体分布函数或经验分布函数, 使用样本顺序比率统计量K分布函数相容性检验效率更高, 可见小子样样本构建样本顺序比率统计量K经验分布函数比小子样样本构建样本经验分布函数精度要好。因此, 可以使用样本顺序比率统计量K的经验分布函数代替概率关联度模型中的经验分布函数。
2.2 变量函数概率关联度模型改进文献[4]提出的概率关联度模型, 使用比较序列样本y1∶n(k)直接构建经验分布函数, 但样本顺序比率统计量K是比较序列样本的函数, 不能直接使用。为了解决该问题, 拓展概率关联度模型的使用范围, 提出了变量函数概率关联度改进模型, 使其能同时应用于样本或样本函数构建经验分布函数。
为便于描述, 首先引入2个引理。
引理1 设X是一连续随机变量, 其分布函数为F(X), 则F(X)服从[0, 1]上的均匀分布。
引理2 设Y=f(X)是一连续随机变量, 其分布函数为F(f(X)), 则F(f(X))服从[0, 1]上的均匀分布。
从上述2个引理可见, 变量或变量函数(变量统计量)均可以代人概率关联度模型中计算概率关联系数, 因此对基本概率关联度模型改进如下:
步骤1 计算k时刻概率关联系数poperator(k)
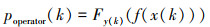
|
(6) |
步骤2 计算概率关联度p, 算子如下
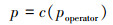
|
(7) |
式中: f(·)为样本函数或样本统计量, 一般为线性或非线性函数关系式, 根据问题背景灵活选择。
变量函数概率关联度改进模型, 可以采用样本或样本函数构建经验分布函数, 来满足小样本概率关联度模型改进使用需求。
注1:通过上述改进, 概率关联度模型适应性更广, 但需要注意的是, 并不是每一种样本/变量函数f(·)都可以参与计算概率关联系数, 这是因为函数计算会引入误差, 或者说抽样误差会通过函数计算放大, 所以选择合适的变量函数或样本统计量很关键。(虽然很难, 但仍可以寻找到一些有用统计量, 即样本函数f(·), 在小样本条件下应用效果较好, 比如文献[9]找到的样本顺序比率统计量K。)
2.3 经验分布函数构造 2.3.1 经验分布函数设x(1), x(2), x(3), …, x(n)为来自分布函数F的随机样本, 其经验分布函数Fn(x)定义为[11]
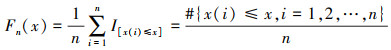
|
(8) |
式中: I[·]为示性函数; #A为集合A中元素的个数。Fn(x)为x的右函数, 共有n个跳跃点, 跳跃度为1/n, 即Fn(xi)-Fn(xi-1)=1/n, i=1, …, n, 且有Fn(-∞)=0, Fn(+∞)=1。
2.3.2 样本容量n < 5经验分布函数构造设样本x=[x(1), x(2), x(3), …, x(n+1)](其中1个样本模拟参考序列样本, 其他样本模拟比较序列样本), 对样本按自小至大顺序排列, 得到样本顺序统计量x′=[x(1), x(2), x(3), …, x(n+1)], 则样本顺序比率统计量Kijk=(x(j)-x(i))/(x(k)-x(i)), 1≤i<j<k≤n+1, 0≤Kijk≤1。
当n=2时, 有1个统计量K123=(x(2)-x(1))/(x(3)-x(1)), 且0≤K123≤1, 对于样本x来自总体X~N(μ, σ2), K123的累积分布函数为[3, 9]
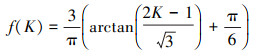
|
(9) |
对于样本x来自其他形式的情况, K123的累积分布函数见文献[9, 12]。当n=3时, 有C43=4个统计量, 分别为K123, K124, K134, K234; 当n=4时, 有C53=10个统计量, 分别为K123, K124, K125, K134, K135, K145, K234, K235, K245, K345; 当n=5时, 有C63=20个统计量, 分别为K123, K124, K125, K126, K134、K135, K136, K145, K146, K156, K234, K235, K236, K245, K246, K256, K345, K346, K356, K456。对于样本量n=3, 4等情况或n更大时, 无法给出Kijk的具体理论分布解析式, 但可以采用数值模拟方法[3]得到Kijk的累积分布函数, 然后计算参考样本在其中的函数值,得到概率关联系数。
2.3.3 样本容量n≥5经验分布函数构造 2.3.3.1 经典Bootstrap方法步骤步骤1 观测样本x=[x(1), x(2), …, x(n)]的值为有限的总体样本, 把n个样本按值自小至大顺序编号排列, 可得到样本的顺序统计量x′=[x(1), x(2), …, x(n)], 式中x(1)=min(x(i)), x(2)=second smallest(x(i)), …, x(n)=max(x(i)),其中,i=1, 2, …, n。用最简洁算法得i处的累积概率分布函数值为
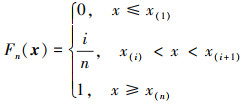
|
(10) |
步骤2 根据原始样本的累积经验分布函数, 得到N组随机抽样集合xk=(x1k, x2k, …, xnk), 其中, k=1, 2, …, N, xk称为Bootstrap样本, 或自助样本。
步骤3 设参数θ是总体的一个未知参数, Fn(x)是由样本得到的累积经验分布函数(样本量为n), 直接可由Fn(x)得到未知参数θ的估计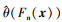
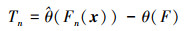
|
(11) |
根据Bootstrap样本集合也可得到参数θ的估计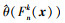
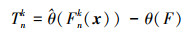
|
(12) |
式中, 由于真实的θ(F)未知, 可由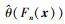
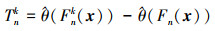
|
(13) |
根据统计理论, 用Tnk分布逼近Tn分布, 当得到大量θ(F)样本后, 运用这些样本即可统计求出参数θ估计值的分布及其特征值。
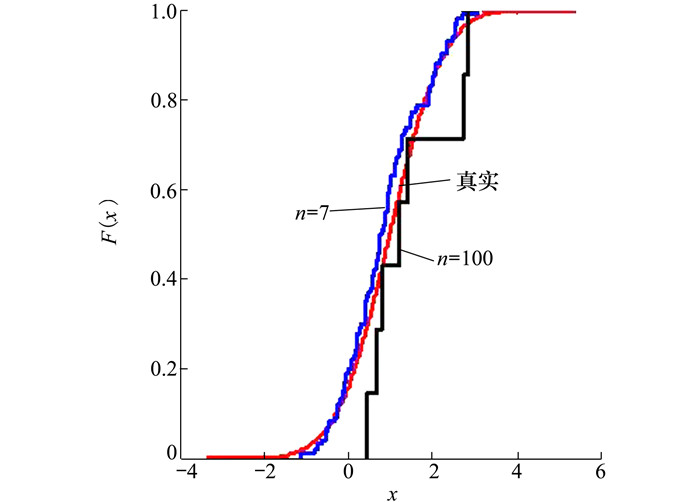
2.3.3.2 Bootstrap方法改进Bootstrap方法通过大量再生子样进行统计推断, 缓解了小样本问题, 但经典的Bootstrap方法的采样方式具有一定局限性, 主要是: ①样本的累积经验分布函数将样本的取值范围限制在[x(1)x(n)]中, 且样本的取值是离散的, 对于连续取值的变量无法获取样本点之外的信息。②从公式(10)可见, 当i=n或x=x(n)时, 有pn=1, 但理论上应是当n→∞, 才有pn=1;同理x=x(1), 有pn=0, 但理论上应是当x→-∞, 有pn=0。图 1给出不同样本构造的经验分布函数及真实分布函数对比。为了普适性应用概率关联度模型, 对基本Bootstrap方法进行修正, 改进的主要思路是:
|
| 图 1 经验分布函数 |
1) 使用样条函数代替原经验分布函数构造使用的阶跃连接, 从而解决了对于连续取值的变量无法获取样本点之外的信息问题。
2) 根据DKW(Dvoretzky-Kiefer-Wolfowitz)不等式, 对经验分布函数的尾概率进行了刻画, 由DKW不等式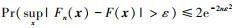

按照以下步骤计算参考序列x和比较序列y之间的小样本概率关联度。
步骤1 计算k时刻概率关联系数poperator(k)
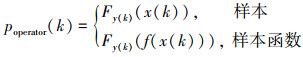
|
(14) |
步骤2 计算概率关联度p
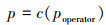
|
(15) |
性质1 小样本概率关联度具有以下基本性质。
1) 规范性, 即0≤p(x, y)≤1;
2) 整体性, 对于不同的相关因素序列xi, xj, 一般有p(xi, xj)≠p(xj, xi), i≠j;
3) 可比性和唯一性;
4) 干扰因素独立性。
性质2 概率关联度不满足偶对称性, 即χ={x, y}, 有p(x, y)≠p(y, x)。
性质3 概率关联度模型不满足数乘变换一致性和平移变换一致性。
3 适用于小样本问题的概率关联分析步骤步骤1 在相同初始条件下, 分别得到参考序列x和比较序列y。
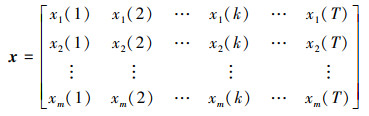
|
(16) |
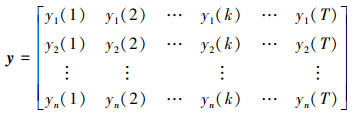
|
(17) |
式中: m为参考序列x1∶m(k)样本容量, n为比较序列y1∶n(k)样本容量,此处可以使用矩阵型概率关联度模型[4]。
步骤2 对参考序列x和比较序列y进行预处理, 使其满足等步长、等长度的数据序列要求。
步骤3 计算k时刻概率关联系数poperator(k)
1) 当y1∶n(k)样本容量n < 5时
① 构建样本顺序比率统计量Kijk=(x(j)-x(i))/(x(k)-x(i)), 1≤i < j < k≤n+1, 0≤Kijk≤1, 并基于样本估计K的经验分布函数Fy1∶n(K)。
② 将参考样本x(k)带入经验分布函数Fy1∶n(K)计算累积分布函数值, 得到关联关联系数poperator(k)。
2) 当y1∶n(k)样本容量n≥5时
① 对比较样本y1∶n(k)使用Bootstrap方法进行重抽样得到重抽样样本y′1∶n(k), 根据重抽样样本y′1∶n(k)估计y的经验分布函数Fy1∶n(y)。
② 将参考样本x(k)带入经验分布函数Fy1∶n(K)计算累积分布函数值, 得到关联系数poperator(k)。
步骤4 决策。检验poperator在一定置信水平α下是否服从[0, 1]上的均匀分布。若通过检验, 说明通过关联分析。否则, 未通过概率关联分析。
4 仿真测试与分析通过几个仿真测试案例验证本文改进模型的正确性和有效性, 仿真案例分别测试样本容量n=2(Kijk有具体理论分布解析式)、n=3(Kijk没有具体理论分布解析式)和样本容量n≥5时(Bootstrap方法改进)的应用场景。
仿真1 参考时间序列X和比较时间序列Y为:
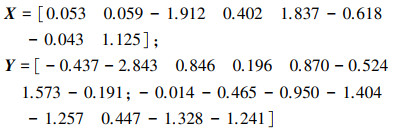
|
检验参考时间序列X和比较时间序列Y的一致性。
比较时间序列Y样本容量n=2, 有1个统计量K123=(x(2)-x(1))/(x(3)-x(1)), 且0≤K123≤1, 累积分布函数为
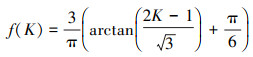
|
(18) |
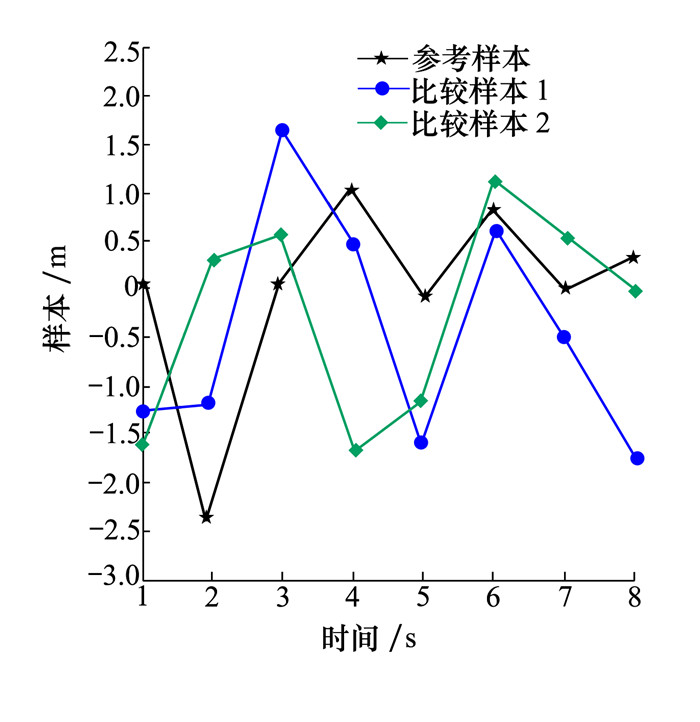
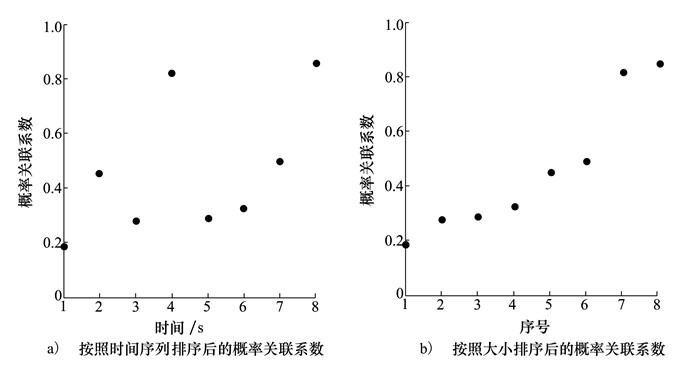
图 2给出了参考时间序列和比较时间序列样本; 将参考时间序列X带入(18)式所示累积分布函数, 得到各个时刻的概率关联系数, 如图 3所示; 图 3b)给出了排序后的概率关联系数。最后计算得到的概率关联度P=0.608 3, 结果: H=0。其中, H表示仿真模型验证结果(kstest函数的计算返回值), 当H=0时, 表示两组数据一致; 当H=1时, 表示两组数据不一致。
|
| 图 2 样本序列 |
|
| 图 3 概率关联系数 |
仿真2 参考时间序列X和比较时间序列Y如下:
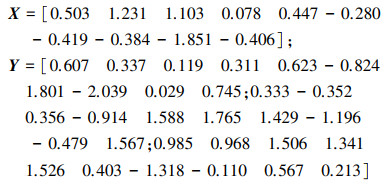
|
检验参考时间序列X和比较时间序列Y的一致性。
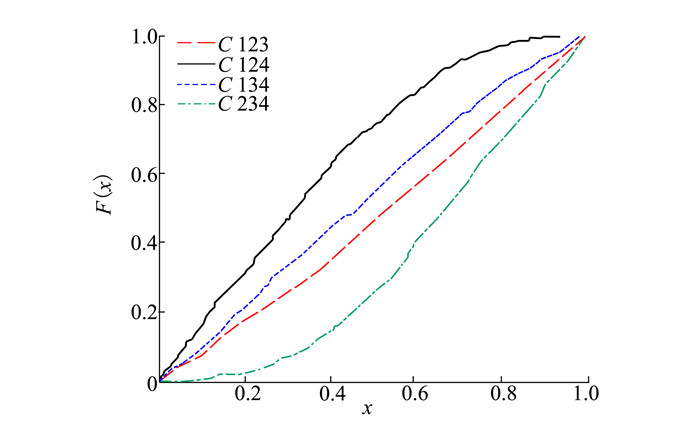
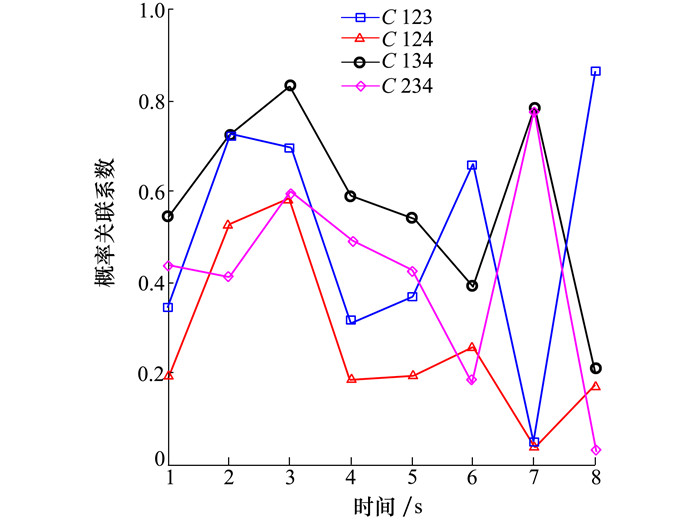
由于比较时间序列Y样本容量n=3时, 样本顺序比率统计量K没有显式表达式, 首先通过数值模拟的方法给出了累积概率密度分布如图 4所示。得到累积分布函数后, 计算参考样本在其中的函数值便可得到概率关联系数。图 5给出了各个时刻的概率关联系数。最后计算得到的概率关联度P=0.716 1, 结果: H=0。
|
| 图 4 n=3时的累积概率密度分布 |
|
| 图 5 概率关联系数 |
仿真3 参考时间序列X和比较时间序列Y如下:

|
检验参考时间序列X和比较时间序列Y的一致性。
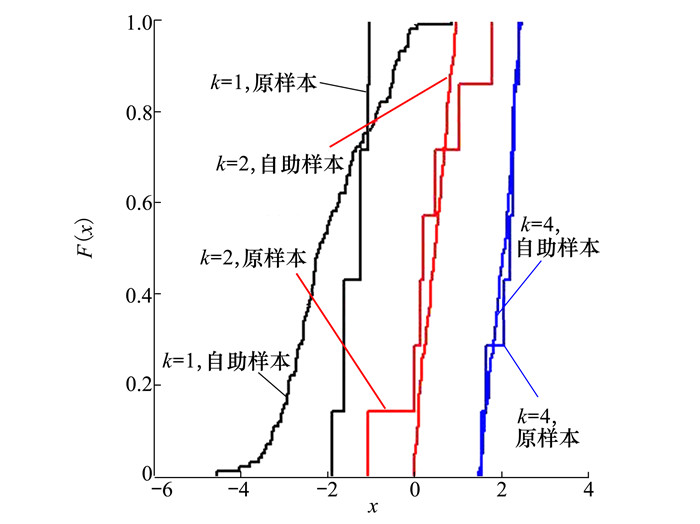
由于k时刻比较序列Y样本容量n≥5, 首先使用Bootstrap方法重抽样, 然后基于重抽样样本构建累积分布函数, 部分结果如图 6所示。由图 6可见, 改进的自助样本构建的累积概率分布函数明显比由原始样本构建的累积概率分布函数光滑。各个时刻的概率关联系数计算结果为[0.162 0.455 0.164 0.152 0.911 0.295 0.286 0.115 0.116 0.015], 最后计算得到的概率关联度P=0.073, 结果: H=1。
|
| 图 6 部分时刻累积分布函数 |
仿真4 参考时间序列X1×10和比较时间序列Y2×10均来自正态分布N(0, 1), 检验参考时间序列X1×10和比较时间序列Y2×10的一致性。分别采用概率关联分析[4]和本文改进的小样本概率关联分析进行检验, 验证本文所提方法的有效性, 共进行10 000次蒙特卡洛实验。很显然, 由于X1×10和Y2×10均来自正态分布N(0, 1), X1×10和Y2×10是一致的, 检验结果应为: H=0。定义误检率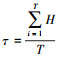
炮射导弹是由坦克炮发射的一种精确制导武器,提高了坦克炮的远距离精确打击能力。研究不同状态下炮射导弹的弹道一致性有利于部队训练使用。由于炮射导弹价格的昂贵性,现场试验组织的复杂性,现场飞行试验样本容量一般为小子样。假设高原、平原2种状态下试验数据如表 3所示,根据炮射导弹的弹道特征[13],选择了3个典型弹道特征点(第一波谷、第一波峰、平稳点)进行一致性检验。
| 状态 | 特征点1 | 特征点2 | 特征点3 |
| S1 | -1.695 4 -1.810 3 |
1.802 8 2.041 7 |
0.378 4 0.860 0 |
| S2 | -1.806 6 -1.317 8 |
1.650 9 0.853 7 |
2.197 9 0.593 6 |
检验结果见表 2,有理由认为这2种状态满足弹道一致性,这与实际现场试验结果相符。
| K | 特征点1 | 特征点2 | 特征点3 | 结果 |
| K123 | 0.032 9 | 0.388 7 | 0.452 8 | H=0, P=0.221 8 |
| K124 | 0.007 7 | 0.277 7 | 0.446 8 | H=0, P=0.211 4 |
| K134 | 0.233 4 | 0.714 4 | 0.986 8 | H=0, P=0.660 9 |
| K234 | 0.227 5 | 0.604 6 | 0.976 1 | H=0, P=0.873 6 |
针对小样本条件下的数据关联分析需求,研究提出了一种小样本概率关联度模型。使用样本函数或样本统计量的累积经验分布函数代替由样本构造的累积经验分布函数,发展拓展了概率关联度模型。当比较序列样本容量n < 5,使用样本样本顺序统计量的经验分布函数计算概率关联系数;当比较序列样本容量n≥5,使用Bootstrap方法重抽样构造经验分布函数计算概率关联系数,解决了小样本比较序列构造的累积概率分布函数误差较大导致概率关联系数计算不准确的问题。仿真案例和实际应用验证了本文方法的合理性和有效性。
| [1] |
高亮, 孙卫, 朱荣昌. 信息不确定条件下时间序列的关联分析法[J]. 西安交通大学学报, 2010, 44(6): 67-71.
GAO Liang, SUN Wei, ZHU Rongchang. A relational analysis approach of time series with uncertain information[J]. Journal of Xi'an Jiaotong University, 2010, 44(6): 67-71. (in Chinese) |
| [2] |
张培忠. 制导炸弹仿真试验技术[M]. 北京: 国防工业出版社, 2019.
ZHANG Peizhong. Guided bomb simulation test technology[M]. Beijing: National Defense Industry Press, 2019. (in Chinese) |
| [3] |
张领科, 赵峰, 余永刚. 一种小子样情况下的弹道一致性评定方法[J]. 兵工学报, 2014, 35(12): 2124-2128.
ZHANG Lingke, ZHAO Feng, YU Yonggang. An evaluation method of ballistic consistency under small sample circumstance[J]. Acta Armamentarii, 2014, 35(12): 2124-2128. (in Chinese) |
| [4] |
宁小磊, 赵新, 吴颖霞, 等. 基于概率关联分析的仿真模型验证方法研究[J]. 西北工业大学学报, 2021: 39.
NING Xiaolei, ZHAO Xin, WU Yingxia, et al. Research on simulation model validation based on probability relational analysis[J]. Northwestern Polytechnical University, 2021: 39. (in Chinese) |
| [5] |
林圣琳, 李伟, 杨明, 等. 考虑相关性的多元输出仿真模型验证方法[J]. 自动化学报, 2019, 45(9): 1666-1678.
LIN Shenglin, LI Wei, YANG Ming, et al. Multivariate validation method under correlation for simulation model[J]. Acta Automatica Sinica, 2019, 45(9): 1666-1678. (in Chinese) |
| [6] |
李伟, 焦松, 陆凌云, 等. 基于特征差异的仿真模型验证及选择方法[J]. 自动化学报, 2014, 40(10): 2134-2144.
LI Wei, JIAO Song, LU Lingyun, et al. Validation and selection of simulation model based on the feature differences[J]. Acta Automatica Sinica, 2014, 40(10): 2134-2144. (in Chinese) |
| [7] |
胡玉伟, 马萍, 杨明, 等. 基于改进灰色关联分析的仿真数据综合一致性检验方法[J]. 北京理工大学学报, 2013, 33(7): 711-715.
HU Yuwei, MA Ping, YANG Ming, et al. A comprehensive consistency test method based on improved grey relational analysis for simulation results[J]. Journal of Beijing Institute of Technology, 2013, 33(7): 711-715. (in Chinese) |
| [8] | EFRON B. Bootstrap methods[J]. The Annuals of Statistics, 1979, 7(1): 1-26. |
| [9] |
唐雪梅. 小样本场合下相容性检验方法[J]. 系统工程与电子技术, 2001, 23(10): 66-68.
TANG Xuemei. Consistency test methods in small sample situation[J]. Systems Engineering and Electronics, 2001, 23(10): 66-68. (in Chinese) |
| [10] |
徐颖强, 陈仙亮, 曹栋波. 样本量为2的极小样本相容性检验方法[J]. 航空学报, 2018, 39(5): 221936.
XU Yingqiang, CHEN Xianliang, CAO Dongbo. Compatibility test method in minimal samples situation with two samples[J]. Acta Aeronauticaet Astronautica Sinica, 2018, 39(5): 221936. (in Chinese) |
| [11] |
杨振海, 程维虎, 张军舰. 拟合优度检验[M]. 北京: 科学出版社, 2011.
YANG Zhenhai, CHENG Weihu, ZHANG Junjian. Goodness of fit test[M]. Beijing: Science Press, 2011. (in Chinese) |
| [12] |
唐雪梅, 张金槐, 邵凤昌, 等. 武器装备小子样试验分析与评估[M]. 北京: 国防工业出版社, 2001.
TANG Xuemei, ZHANG Jinhuai, SHAO Fengchang, et al. Test analysis and evaluation of weapon systems in samll-sample circumstance[M]. Beijing: National Defense Industry Press, 2001. (in Chinese) |
| [13] |
邱荣剑, 张永录. 驾束制导导弹仿真系统的可信度评估[J]. 装备制造技术, 2011(2): 27-28.
QIU Rongjian, ZHANG Yonglu. Trustworthiness assessment of beam ride missile simulation system[J]. Equipment Manufactring Technology, 2011(2): 27-28. (in Chinese) |
2. Xi'an Modern Control Technology Research Institute, Xi'an 710065, China;
3. School of Astronautics, Northwestern Polytechnical University, Xi'an 710072, China




