日本科学家于1980年最先提出了功能梯度材料(functionally graded material, FGM)的概念。功能梯度材料是一种具有非均匀微观力学结构的复合材料, 通常由陶瓷和金属组成。功能梯度材料起初由于其中陶瓷部分较好的耐热性和金属部分良好的机械强度而被用于核工业以及航空航天结构的热障材料。与传统复合材料相比, 功能梯度材料确保了应力分布的平稳过渡、应力集中的最小化, 同时增加了2种不同材料界面的结合强度。后来随着世界各国大量学者的深入研究, 功能梯度材料在各个领域都得到了重视, 广泛应用于航空航天、电子、光学、化学、生物医学、核工程和土木工程等方面[1]。
近30年来功能梯度材料及结构的力学行为分析一直是各国学者持续研究的热点, 具体成果可参见Carrera、Reddy和Chakraverty等[2-4]诸多学者的研究工作。近年来, Bouamama等[5]基于经典梁理论(CBT)和E-FGM模型, 推导出功能梯度材料梁自由振动频率的精确解, 分析了不同边界条件对功能梯度材料梁自由振动基频的影响。Safa等[6]和Chen等[7]基于梁的高阶剪切变形理论, 考虑了梁厚度方向的均匀温度、线性温度和非线性温度三种分布以及材料性质的温度依赖, 分别应用Navier法和Rayleigh-Ritz法结合改进的Fourier级数给出了功能梯度材料梁的热-弹振动响应的解答, 分析了温度分布、材料参数、细长比和边界条件等对功能梯度材料梁固有频率的影响。Xia等[8]基于三阶剪切变形理论, 导出了功能梯度材料Reddy-Bickford梁的静态弯曲解与相应的均质Euler-Bernoulli梁静态弯曲解的转换关系, 实现了剪切变形的非均匀功能梯度材料梁经典化弯曲的响应和均匀化表示。Li等[9]基于一种具有Reddy剪切函数的简单拟三维理论和一种新的三角剪切函数, 研究了在Winkler、Pasternak和Kerr弹性地基上功能梯度材料矩形板的动态响应问题。Simsek[10]基于梁的各种高阶剪切理论, 研究了功能梯度材料梁在不同边界条件和高阶剪切理论下的自由振动问题, 分析了不同边界条件下梁的细长比梯度指数在对功能梯度材料梁横向自由振动的影响。从已有文献来看, 目前关于功能梯度材料及结构力学行为的分析大多可归结为线性问题, 但由于非线性问题远比线性问题复杂, 从而对其非线性静动态力学行为的分析相对较少。随着技术的进步和设计的精细化要求, 对功能梯度材料及结构的力学行为进行非线性分析也非常必要。
功能梯度材料在实际生产过程中, 由于制备方法和工艺等缺陷, 不可避免在材料内部产生孔隙。这些孔隙对功能梯度材料的物理性质和功能应用有着较大的影响, 因此越来越多的科研人员已经开始关注多孔功能梯度材料及结构的力学行为研究。滕等[11]基于经典薄板理论, 采用微分变换法(differential transformation method, DTM)研究了不同孔隙分布对四边受压多孔功能梯度材料矩形板静动态力学行为的影响。Zhao等[12]研究了具有均匀弹性边界条件的功能梯度多孔矩形板的自由振动问题。
目前, 对于多孔功能梯度材料Timoshenko梁的非线性自由振动分析的研究还鲜有文献报道。本文基于Timoshenko梁变形理论, 将针对多孔功能梯度材料梁的孔隙均匀分布和孔隙线性分布2种形式, 根据广义Hamilton原理推导多孔功能梯度材料Timoshenko梁非线性自由振动的控制微分方程组, 采用DTM变换求解并分析不同边界条件下梯度指数、孔隙率和细长比对多孔功能梯度材料Timoshenko梁动态响应的影响。将其退化为无孔隙的功能梯度材料Timoshenko梁的非线性自由振动和线性自由振动后, 所得非线性固有频率比值和线性固有频率与已有文献的结果进行对照, 以验证DTM求解的有效性和正确性。
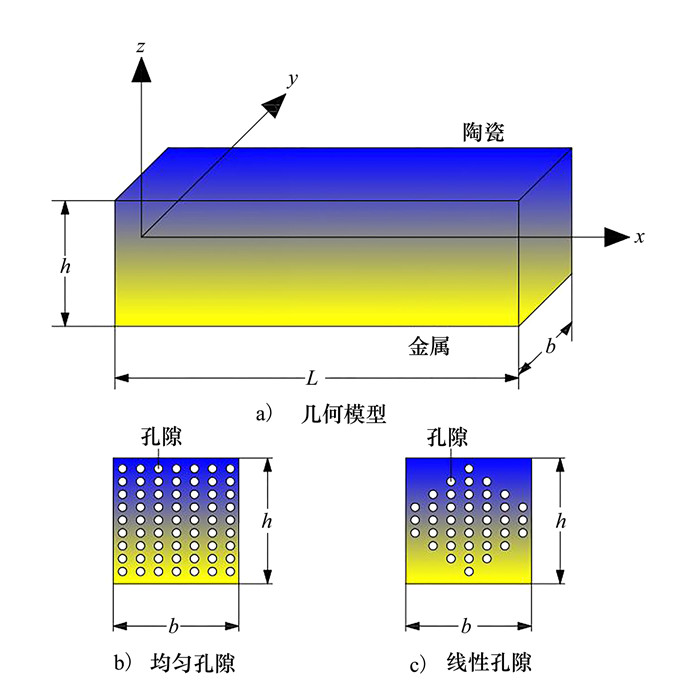
1 数学模型的建立及材料物性参数的描述考虑如图 1所示多孔功能梯度材料Timoshenko矩形截面梁, 取梁的轴线方向、宽度方向和厚度方向分别为x轴、y轴和z轴, 建立笛卡尔三维坐标系xyz。梁的长为L, 宽为b, 高为h。
|
| 图 1 多孔功能梯度材料Timoshenko梁的几何模型和截面上的2种孔隙分布 |
梁的材料由陶瓷和金属复合而成, 材料组分由下表面含孔隙的完全金属材料连续变化到上表面含孔隙的完全陶瓷材料, 且材料性质沿厚度方向呈梯度分布, 梁的主要物理参数P (弹性模量E、切变模量G、质量密度ρ、泊松比v) 均是关于坐标z的函数。由下列混合律模型[13]统一给出
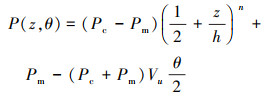
|
(1) |
式中: -0.5h≤z≤0.5h, n为梯度指数, 下标c与m分别表示陶瓷和金属材料, θ表示孔隙率, Vu表示孔隙分布模型。这里仅考虑均匀孔隙和线性孔隙这2种常见的孔隙分布, Vu的取值分别为Vu=1和Vu=(1-2|z|/h)。
2 控制微分方程及参数的无量纲化基于Timoshenko梁理论, 多孔功能梯度材料梁的位移场可表示为

|
(2) |
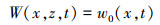
|
(3) |
式中: u0表示梁几何中面上沿x轴方向的位移;w0表示梁几何中面上沿z轴方向的位移;ϕ表示梁横截面上的转角;t表示时间。则多孔功能梯度材料Timoshenko梁的位移与应变的关系可表示为
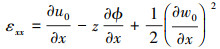
|
(4) |
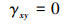
|
(5) |
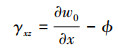
|
(6) |
式中: εxx表示梁截面上任一点的线应变; γxy和γxz为梁的切应变。系数定义如下
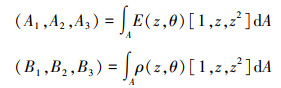
|
式中: A1, A2和A3分别称为梁的拉伸刚度、拉-弯耦合刚度和弯曲刚度; B1, B2和B3称为梁的截面惯性系数。则梁的弯曲应变能为
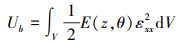
|
(7) |
将(4)式代入(7)式得

|
(8) |
将(8)式展开得
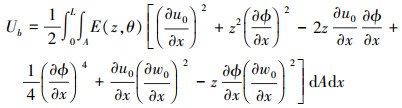
|
(9) |
由剪切变形产生的应变能为
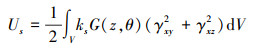
|
(10) |
将(5)式和(6)式代入(10)式得
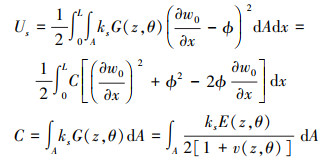
|
(11) |
式中: C为剪切刚度; ks为剪切修正系数, 本文分析的梁为矩形截面, 根据参考文献[10], 矩形截面梁的ks=5/6。将(9)式与(11)式相加, 得梁的总应变能为
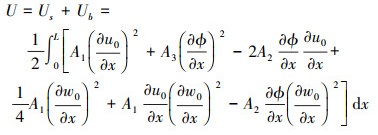
|
(12) |
梁的动能为
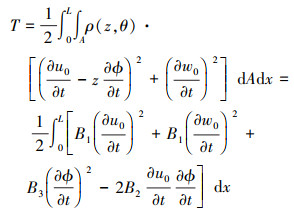
|
(13) |
引入下列无量纲系数
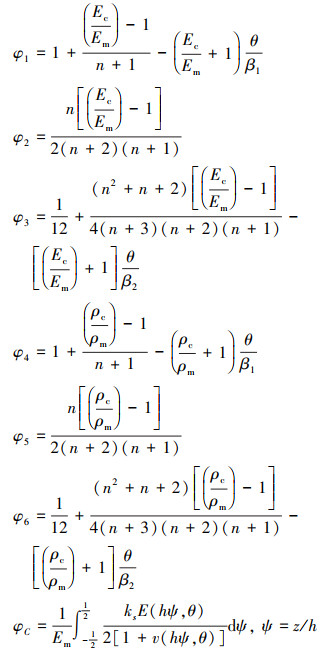
|
式中: 孔隙均匀分布时β1=2, β2=24;孔隙线性分布时β1=4, β2=96。由此将刚度系数等表示为
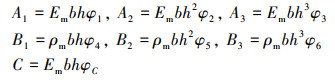
|
根据(12)~(13)式, 采用广义Hamilton原理[14]
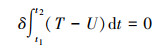
|
(14) |
式中: δ为变分符号;t1和t2分别表示系统运动的开始时间和结束时间。将(14)式展开并整理, 得到梁横向运动的控制微分方程组
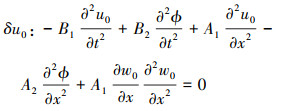
|
(15) |
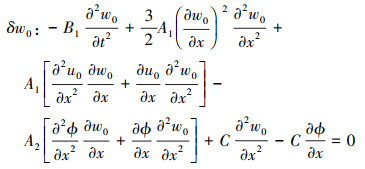
|
(16) |
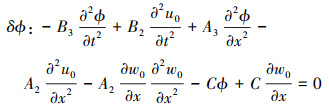
|
(17) |
由于梁在轴向的位移非常微小, 根据文献[15]的处理方法, 将梁近似视为轴向不可移动, 因此忽略(15)~(17)
式中关于u0的惯性项, 并将无量纲系数代入, 将方程组进一步化为
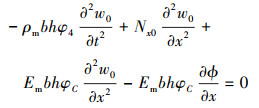
|
(18) |
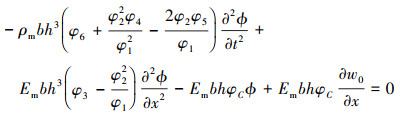
|
(19) |
式中: Nx0为大振幅产生的轴向拉伸力, 其计算式为
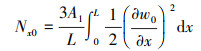
|
对于功能梯度材料梁的自由振动, 可令

|
(20) |
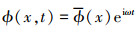
|
(21) |
式中: w, ϕ分别表示关于w0和ϕ的模态函数;e为自然底数;i为虚数单位;ω为梁的固有频率。
将(20)~(21)式代入(18)~(19)式并进行化简, 得到梁的非线性自由振动的控制微分方程组
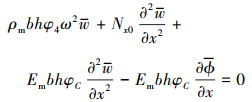
|
(22) |
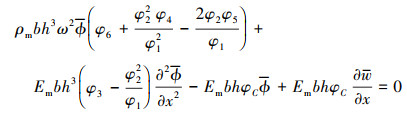
|
(23) |
对(22)~(23)式进行如下无量纲化
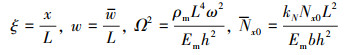
|
式中: Ω为无量纲固有频率; Nx0为大振幅产生的无量纲轴向拉伸力; kN为大挠度轴力修正系数, 本文同文献[15]一致取kN=3/4。这样可得梁的无量纲自由振动控制微分方程为
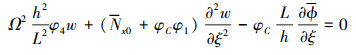
|
(24) |
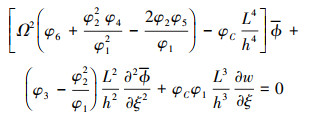
|
(25) |
对于多孔功能梯度材料Timoshenko梁的边界条件只考虑工程实际中常见的情况[16]
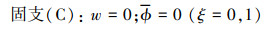
|
(26) |
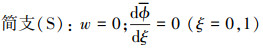
|
(27) |
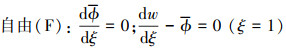
|
(28) |
微分变换法(DTM) 基于泰勒级数展开, 能有效将线性或非线性微分方程变换为代数方程进行求解的一种半解析方法, 其优点是求解过程简单、精度较高, 编程方便。利用该方法, 可将给定的偏微分方程和相应的边界条件转化为一个递推方程, 最终得到一个代数方程组的解为幂级数的系数解。该方法适用于线性和非线性常微分方程和偏微分方程的精确和近似解, 不需要线性化和摄动, 避免了大量的计算工作和舍入误差。许多研究结果[11, 17]都很好地验证了该方法在求解微分方程特征值问题时的实用性和有效性。运用DTM对控制方程组进行求解时, 首先需要将其无量纲控制微分方程组根据边界条件经DTM变换为相应的代数特征方程组, 其具体变换过程可参考文献[17]。这里用W1和W2表示经DTM变换后关于w和ϕ的变换函数, 则控制微分方程组(24)~(25)式经DTM变换为
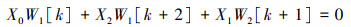
|
(29) |
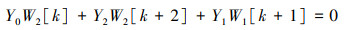
|
(30) |
式中
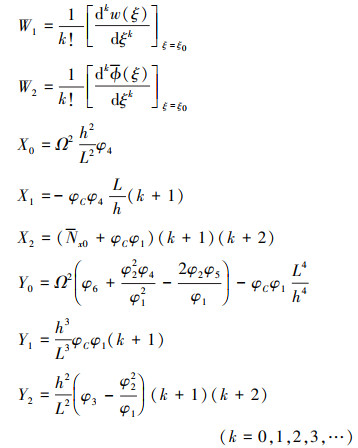
|
对边界条件也进行DTM变换:
在ξ=0处
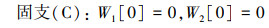
|
(31) |
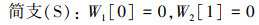
|
(32) |
在ξ=1处
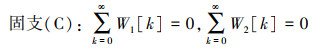
|
(33) |
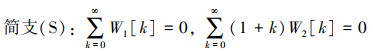
|
(34) |
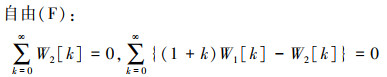
|
(35) |
将方程(29)~(30)式代入C-C、C-S、S-S、C-F 4种边界条件中, 得对应的频率特征方程
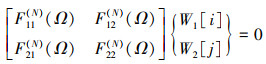
|
(36) |
式中, F11(N) (Ω), F12(N) (Ω), F21(N)(Ω)和F22(N)(Ω)是经迭代N次求出的含有以无量纲固有频率Ω为未知量的多项式。当边界条件为C-C、C-S和C-F时, i=1, j=1;S-S时, i=1, j=0。(36)式的方程有解, 则存在等式
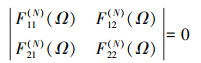
|
(37) |
最终根据(37)式即可得到无量纲固有频率Ω的解。
4 计算结果及分析指定DTM程序的迭代次数N, 令wmax=0, 使控制方程中非线性项为0, 求出收敛的线性无量纲固有频率; 根据不同的边界条件下梁产生最大挠度的位置从而确定对应的无量纲位置系数K和振幅, 求出对应的Nx0并代入(29)~(30)式; 求出收敛的非线性无量纲固有频率, 从而得到非线性无量纲固有频率比值。令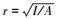
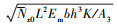
为了验证本文解的正确性, 通过令孔隙率θ为0, 将多孔功能梯度材料Timoshenko梁退化为无孔隙的功能梯度材料Timoshenko梁并与已有文献进行对照, 对照分析具体见表 1。该例在计算时同文献[18]一样, 取钨(W)为陶瓷材料, 取铜(Cu)为金属材料, 材料参数为Ec=411 GPa, Em=120 GPa, ρc=19 250 kg/m3, ρm=8 960 kg/m3, vc=vm=0.3。此表是在4种边界条件下取梁的细长比L/h=8与梯度指数n=1时, wmax/r分别为0, 0.2, 0.4, 0.6, 0.8和1时, 无孔隙的功能梯度材料Timoshenko梁通过DTM求解出的非线性无量纲固有频率比值与文献[18]所得数据的对比, 并给出两者之间计算结果的相对误差。通过此算例可知本文退化方程的计算数据与文献数据基本一致, 其最大误差仅在0.4%以内, 说明了DTM对于本文研究的有效性和正确性。
| 边界 | 方法 | wmax/r | |||||
| 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 | ||
| S-S | 本文 文献[18] 相对误差/% |
1.000 000 1.000 000 0 |
1.003 425 1.003 063 0.036 105 |
1.013 631 1.011 241 0.235 804 |
1.030 416 1.026 542 0.376 023 |
1.053 466 1.050 426 0.288 628 |
1.082 382 1.083 644 0.116 451 |
| C-S | 本文 文献[18] 相对误差/% |
1.000 000 1.000 000 0 |
1.002 152 1.002 508 0.035 501 |
1.008 578 1.008 589 0.001 061 |
1.019 190 1.018 867 0.031 727 |
1.033 847 1.033 384 0.044 827 |
1.052 365 1.052 085 0.026 571 |
| C-C | 本文 文献[18] 相对误差/% |
1.000 000 1.000 000 0 |
1.001 187 1.003 832 0.263 461 |
1.004 739 1.007 201 0.244 399 |
1.012 784 1.012 784 0.212 930 |
1.020 536 1.020 536 0.169 660 |
1.029 207 1.030 396 0.115 358 |
| C-F | 本文 文献[18] 相对误差/% |
1.000 000 1.000 000 0 |
1.000 064 1.001 903 0.183 502 |
1.000 258 1.001 860 0.159 911 |
1.000 580 1.001 787 0.120 469 |
1.001 031 1.001 686 0.065 386 |
1.001 787 1.001 787 0 |
下面分析在两种孔隙分布模型和不同边界条件下梯度指数n、细长比L/h、最大挠度值wmax和孔隙率θ等不同参数对非线性无量纲固有频率比值的影响。对于多孔功能梯度材料Timoshenko梁, 采用算例1所示的材料参数。
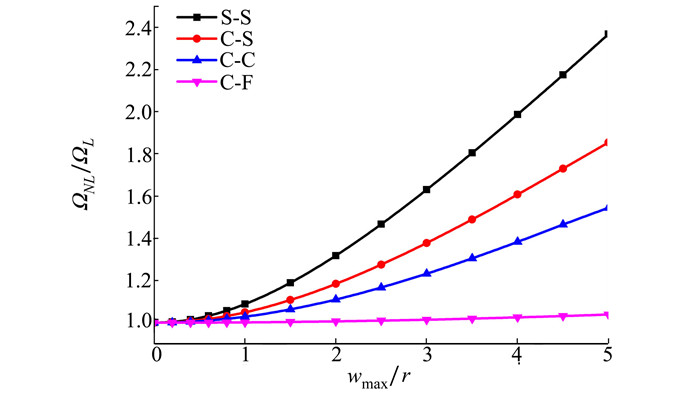
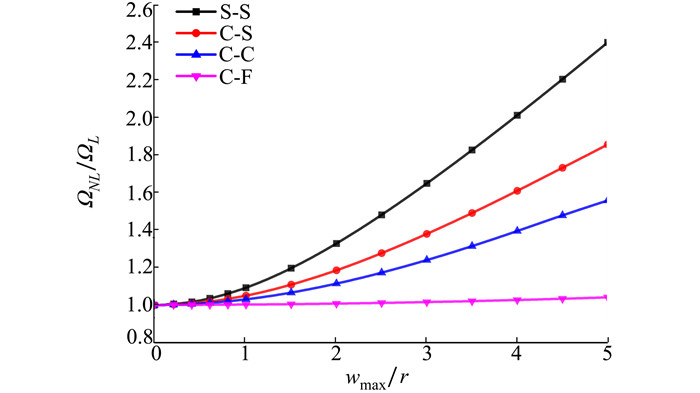
图 2和图 3分别给出了多孔功能梯度材料Timoshenko梁采用线性孔隙分布模型与均匀孔隙分布模型, 在S-S、C-S、C-C和C-F 4种边界条件下, 取细长比L/h=20, 梯度指数n=1, 孔隙率θ=0.1时, wmax/r与非线性无量纲固有频率比ΩNL/ΩL的关系曲线。
|
| 图 2 不同边界条件下最大挠度值wmax对线性孔隙分布的多孔功能梯度材料Timoshenko梁非线性无量纲固有频率比值ΩNL/ΩL的影响(h/L=1/20, n=1, θ=0.1) |
|
| 图 3 不同边界条件下最大挠度值wmax对均匀孔隙分布的多孔功能梯度材料Timoshenko梁非线性无量纲固有频率比值ΩNL/ΩL的影响(h/L=1/20, n=1, θ=0.1) |
由图可知, 随着wmax/r的增加, 4种边界条件下的无量纲固有频率比值均呈现上升趋势, 其中S-S频率比值的上升趋势最明显, C-F频率比值的变化趋势最平缓。
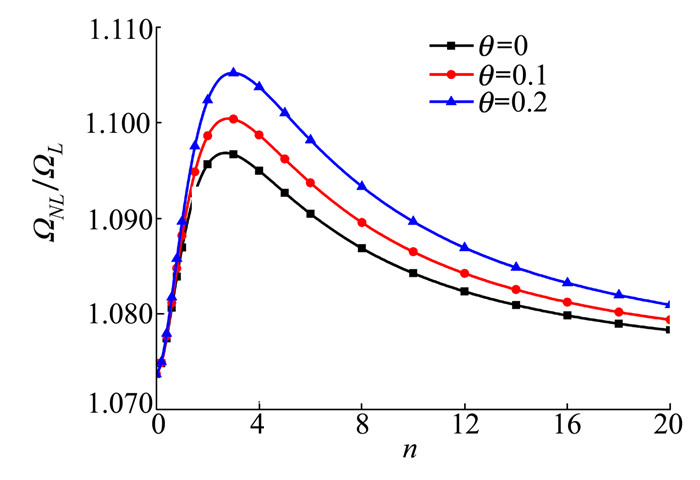
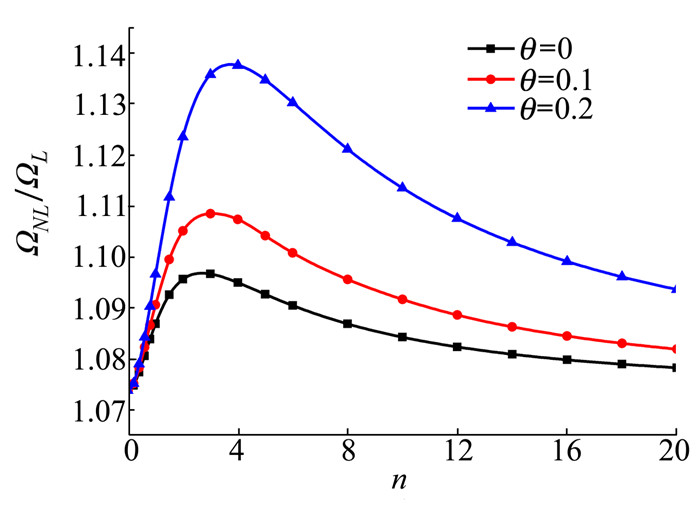
图 4~11分析了多孔功能梯度材料Timoshenko梁在不同边界条件、不同孔隙率和线性与均匀2种孔隙分布下, 取L/h=20和wmax/r=1时频率比值ΩNL/ΩL与梯度指数n的关系。图 4和图 5分别给出了S-S边界条件的多孔功能梯度材料Timoshenko梁在线性孔隙和均匀孔隙2种分布模型下, 梯度指数n与非线性无量纲固有频率比值的关系曲线。由此得出孔隙率θ与频率比呈正相关的结论, 其中在均匀孔隙分布下频率比值随孔隙率θ增加而上升的幅度比线性孔隙的大。2种孔隙分布下的梯度指数n对频率比值的影响均在0~3内最明显, 之后趋于稳定。
|
| 图 4 S-S边界条件下不同孔隙率θ和梯度指数n对线性孔隙分布的多孔功能梯度材料Timoshenko梁非线性无量纲固有频率比值ΩNL/ΩL的影响(L/h=20, wmax/r=1) |
|
| 图 5 S-S边界条件下不同孔隙率θ和梯度指数n对均匀孔隙分布的多孔功能梯度材料Timoshenko梁非线性无量纲固有频率比值ΩNL/ΩL的影响(L/h=20, wmax/r=1) |
|
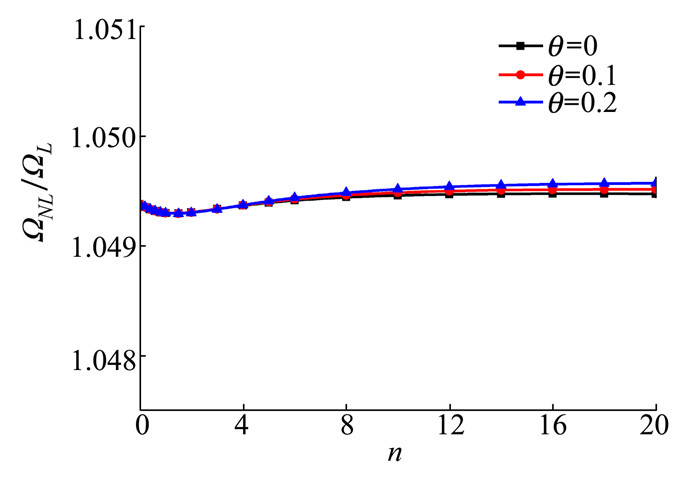
| 图 6 C-S边界条件下不同孔隙率θ和梯度指数n对线性孔隙分布的多孔功能梯度材料Timoshenko梁非线性无量纲固有频率比值ΩNL/ΩL的影响(L/h=20, wmax/r=1) |
|
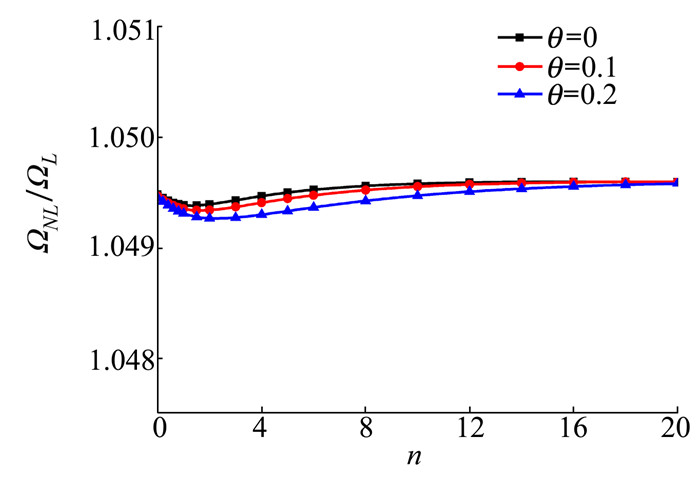
| 图 7 C-S边界条件下不同孔隙率θ和梯度指数n对均匀孔隙分布的多孔功能梯度材料Timoshenko梁非线性无量纲固有频率比值ΩNL/ΩL的影响(L/h=20, wmax/r=1) |
|
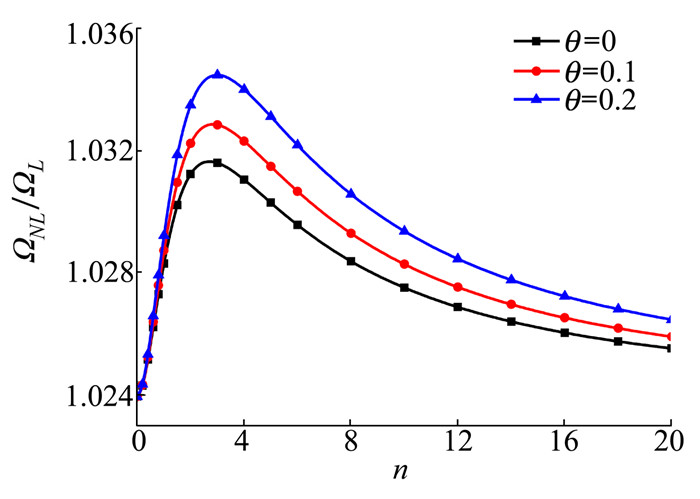
| 图 8 C-C边界条件下不同孔隙率θ和梯度指数n对线性孔隙分布的多孔功能梯度材料Timoshenko梁非线性无量纲固有频率比值ΩNL/ΩL的影响(L/h=20, wmax/r=1) |
|
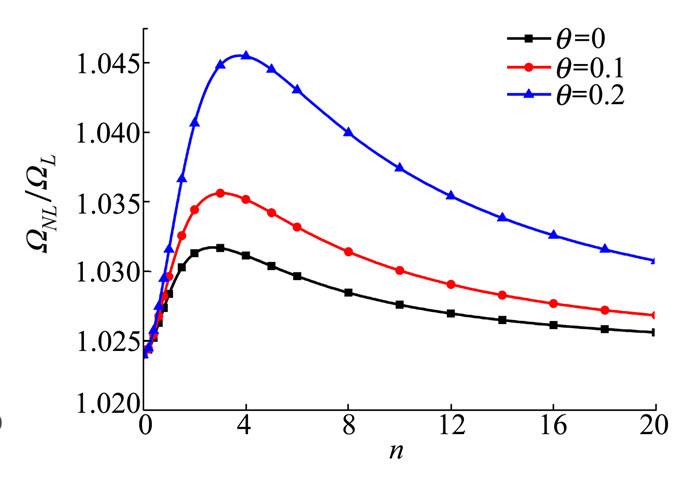
| 图 9 C-C边界条件下不同孔隙率θ和梯度指数n对均匀孔隙分布的多孔功能梯度材料Timoshenko梁非线性无量纲固有频率比值的影响(L/h=20, wmax/r=1) |
|
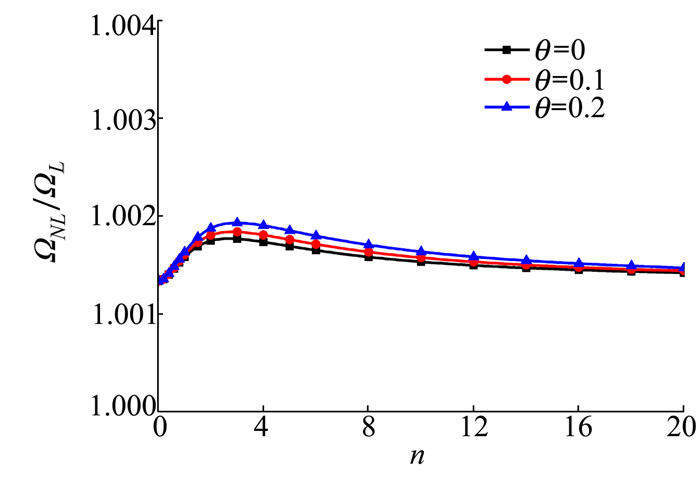
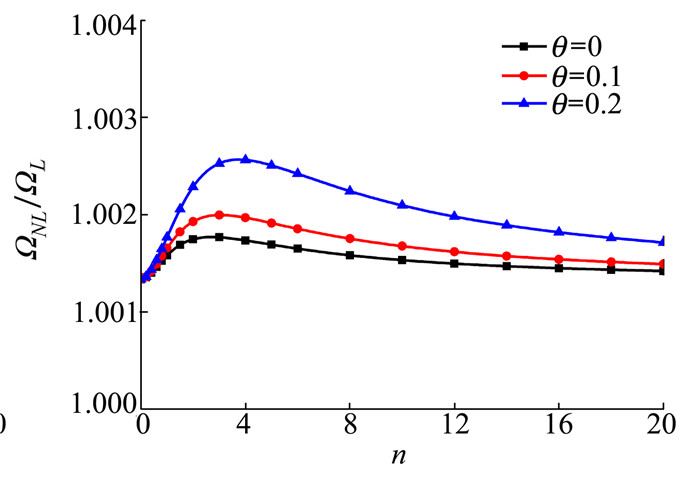
| 图 10 C-F边界条件下不同孔隙率θ和梯度指数n对线性孔隙分布的多孔功能梯度材料Timoshenko梁非线性无量纲固有频率比值的影响(L/h=20, wmax/r=1) |
|
| 图 11 C-F边界条件下不同孔隙率θ和梯度指数n对均匀孔隙分布的多孔功能梯度材料Timoshenko梁非线性无量纲固有频率比值的影响(L/h=20, wmax/r=1) |
从图 6和图 7可知, 多孔功能梯度材料Timoshenko梁在C-S边界条件下, 自振频率比值随梯度指数n增加而变化的幅度不太明显, 2种孔隙分布下的关系曲线都仅当n在0~3的之间内才能看出频率比值随n的细微改变。另外发现, 孔隙按线性分布时频率比值与孔隙率θ呈正相关, 但值得注意的是孔隙按均匀分布时频率比值与孔隙率θ呈负相关。
根据图 8和图 9对C-C边界条件下线性孔隙和均匀孔隙的多孔功能梯度材料Timoshenko梁无量纲频率比值与梯度指数n关系曲线的描绘可知, 频率比值与孔隙率θ均呈正相关, 且频率比值的变化在n处于0~3之间最活跃, 之后逐渐趋于稳定。同时还发现均匀孔隙分布下的频率比值随孔隙率θ增加而上升的幅度比线性孔隙的大。
由图 10和图 11可知, 在C-F边界条件和2种孔隙分布下多孔功能梯度材料Timoshenko梁的自振频率比值与孔隙率θ均呈正相关, 频率比值关于梯度指数n的变化程度均在n处于0~3之间时比较活跃, 之后逐渐趋于稳定。同时在均匀孔隙分布下的频率比值随孔隙率θ增加而上升的幅度比线性孔隙的大。
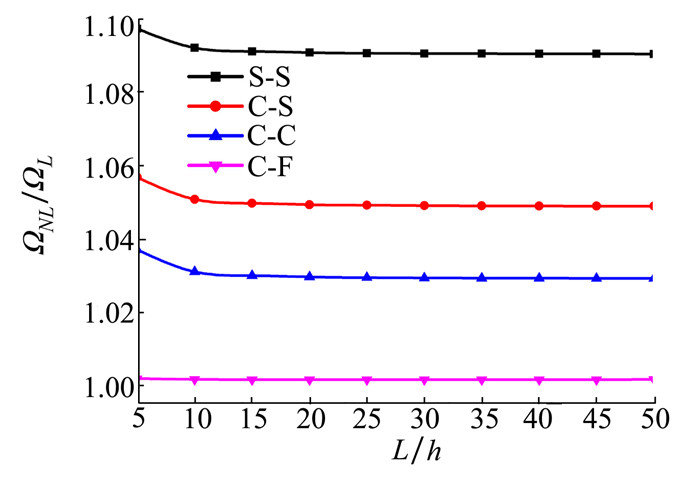
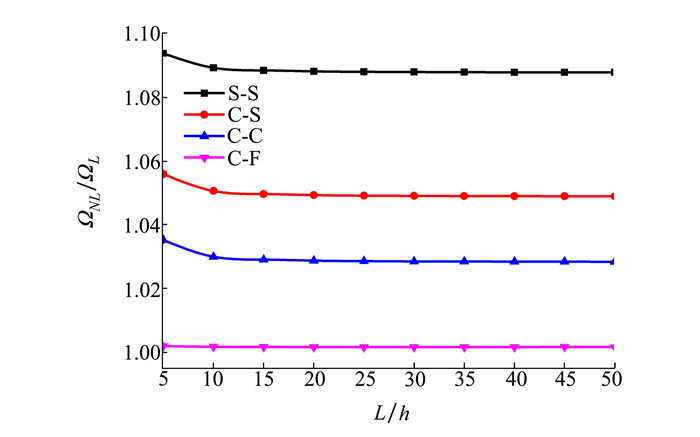
图 12和图 13给出了n=1, wmax/r=1和θ=0.1时不同边界条件下细长比L/h对2种分布孔隙的多孔功能梯度材料Timoshenko梁非线性无量纲固有频率比值的影响。就整体趋势来看可发现, 多孔功能梯度材料Timoshenko梁在2种孔隙分布下, 频率比值关于细长比L/h的变化趋势和幅度都保持基本一致。在S-S、C-S和C-C 3种边界条件下, 关于2种孔隙分布的频率比值均在细长比L/h处于5~10之间时最明显, 在C-F边界条件下的变化趋势不明显, 其整体曲线趋于平缓。
|
| 图 12 不同边界条件下细长比L/h对均匀孔隙分布的多孔功能梯度材料Timoshenko梁非线性无量纲固有频率比值的影响(n=1, wmax/r=1, θ=0.1) |
|
| 图 13 不同边界条件下细长比L/h对线性孔隙分布的多孔功能梯度材料Timoshenko梁非线性无量纲固有频率比值的影响(n=1, wmax/r=1, θ=0.1) |
本文采用微分变换法(DTM)对多孔功能梯度材料Timoshenko梁在孔隙为均匀和线性2种分布情况下的非线性自由振动进行求解。将退化的求解结果与已有文献数据对比, 验证了求解方法的有效性和正确性。最后分析了孔隙率、梯度指数、最大挠度值、细长比和边界条件对功能梯度材料Timoshenko梁非线性无量纲固有频率比值的影响。主要结论如下:
1) 材料参数一定的情况下, 频率比值随着最大挠度值的增加而增加, 其中S-S边界条件下增加的趋势最明显, C-F下的变化最微小。
2) 频率比值随梯度指数的变化程度, 在S-S边界条件下最明显, 在C-S下较微小。4种边界条件下的频率比值均在梯度指数处于0~3时变化最剧烈。
3) C-S边界条件下均匀孔隙分布的频率比值随孔隙率的增大而减小, 其余的频率比值均随孔隙率的增大而增大, 且均匀孔隙分布下的变化程度均比线性孔隙分布下显著。
| [1] | SALEH B, JIANG J, FATHI R, et al. 30 Years of functionally graded materials: an overview of manufacturing methods, applications and future challenges[J]. Composites Part B: Engineering, 2020, 201: 108376. DOI:10.1016/j.compositesb.2020.108376 |
| [2] | CARRERA E, BRISCHETTO S, ROBALDO A. Variable kinematic model for the analysis of functionally graded material plates[J]. AIAA, 2006, 46(1): 194-203. |
| [3] | REDDY J N, CHIN C D. Thermomechanical analysis of functionally graded cylinders and plates[J]. Journal of Thermal Stresses, 1998, 21: 593-626. DOI:10.1080/01495739808956165 |
| [4] | CHAKRAVERTY S, PRADHAN K K. Free vibration of exponential functionally graded rectangular plates in thermal environm-ent with general boundary conditions[J]. Aerospace Science and Technology, 2014, 36: 132-156. DOI:10.1016/j.ast.2014.04.005 |
| [5] | BOUAMAMA M, EIMEICHE A, ELHENNANI A, et al. Exact solution for free vibration analysis of FGM beams[J]. Journal of Composite and Advanced Materials, 2020, 30(2): 55-60. |
| [6] | SAFA A, HADJI L, BOURADA M, et al. Thermal vibration analysis of FGM beams using an efficient shear deformation beam theory[J]. Earthquakes and Structures, 2019, 17(3): 329-336. |
| [7] | CHEN Y, JIN G, ZHANG C, et al. Thermal vibration of FGM beams with general boundary conditions using a higher-order shear deformation theory[J]. Composites Part B: Engineering, 2018, 153: 376-386. DOI:10.1016/j.compositesb.2018.08.111 |
| [8] | XIA Y, LI S, WAN Z. Bending solutions of FGM Reddy-Bickford beams in terms of those of the homogenous Euler-Bernoulli beams[J]. Acta Mechanica Solida Sinica, 2019, 32(29): 499-516. |
| [9] | LI M, GUEDES SOARES C, YAN R. Free vibration analysis of FGM plates on Winkler/Pasternak/Kerr foundation by using a simple quasi-3D HSDT[J]. Composite Structures, 2021, 264: 113643. DOI:10.1016/j.compstruct.2021.113643 |
| [10] | SIMSEK M. Fundamental frequency analysis of functionally graded beams by using different higher-order beam theories[J]. Nuclear Engineering and Design, 2010, 240(4): 697-705. DOI:10.1016/j.nucengdes.2009.12.013 |
| [11] |
滕兆春, 席鹏飞. 多孔FGM矩形板的自由振动与临界屈曲载荷分析[J]. 西北工业大学学报, 2021, 39(2): 317-325.
TENG Zhaochun, XI Pengfei. Analysis on free vibration and critical buckling load of a FGM porous rectangular plate[J]. Journal of Northwestern Polytechnical University, 2021, 39(2): 317-325. (in Chinese) |
| [12] | ZHAO J, WANG Q, DENG X, et al. Free vibrations of functionally graded porous rectangular plate with uniform elastic boundary conditions[J]. Composites Part B: Engineering, 2019, 168: 106-120. DOI:10.1016/j.compositesb.2018.12.044 |
| [13] | KIRAN M C, KATTIMANI S C, VINYAS M. Porosity influence on structural behavior of skew functionally graded magneto-electro-elastic plate[J]. Composite Structures, 2018, 191: 36-77. DOI:10.1016/j.compstruct.2018.02.023 |
| [14] | RAO S S. Vibration of continuous systems[M]. 2nd ed. Hoboken: John Wiley and Sons, 2019. |
| [15] | WATTANASAKULPONG N, UNGBHAKORN V. Linear and nonlinear vibration analysis of elastically restrained ends FGM beams with porosities[J]. Aerospace Science and Technology, 2014, 32(1): 111-120. DOI:10.1016/j.ast.2013.12.002 |
| [16] | EBRAHIMI F, MOKHTARI M. Transverse vibration analysis of rotating porous beam with functionally graded microstructure using the differential transform method[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2015, 37(4): 1435-1444. DOI:10.1007/s40430-014-0255-7 |
| [17] | GHAZARYAN D, BURLAYENKO V N, AVETISYAN A, et al. Free vibration analysis of functionally graded beams with non-uniform cross-section using the differential transform method[J]. Journal of Engineering Mathematics, 2018, 110(1): 97-121. DOI:10.1007/s10665-017-9937-3 |
| [18] | XIE K, WANG Y, FAN X, et al. Nonlinear free vibration analysis of functionally graded beams by using different shear deformation theories[J]. Applied Mathematical Modelling, 2020, 77(2): 1860-1880. |



