2. 西北工业大学 航天学院, 陕西 西安 710072;
3. 西安现代控制技术研究所, 陕西 西安 710065
材料失效是一个复杂的渐进变化过程, 在载荷的作用下, 材料中的应力和应变不断积累, 在到达材料的破坏点之后, 损伤开始发生, 材料内部形成微观裂纹, 随着载荷继续增加, 裂纹不断扩展, 逐步形成宏观裂纹, 最终导致材料破坏[1-2]。研究材料失效过程的分析方法可大致分为连续损伤力学(CDM)方法和断裂力学(FM)方法[3-4]。连续损伤力学主要研究材料内部微观结构缺陷的萌生、汇合、扩展所造成的材料宏观力学性能的局部劣化, 通过对材料的本构关系衰减研究来反映损伤的影响[5-6]。根据损伤机理的不同, 可以建立相应的损伤判别准则和损伤演化方程, 将损伤判别准则引入到材料的本构关系中, 则可对整个分析过程的损伤程度进行描述。断裂力学主要研究宏观裂纹对材料强度的影响, 该方法对裂纹扩展进行模拟, 以描述缺陷和破坏的累积[7]。
材料失效过程涉及非线性应力、应变变化, 裂纹起始和扩展过程等问题, 一般难以进行解析分析。因此, 在结构和力学研究领域, 数值仿真模拟已经成为分析材料失效过程的重要手段。数值分析方法通常可以分为离散方法和弥散方法。离散方法如虚拟裂纹闭合技术(VCCT)[8]、扩展有限元法(XFEM)[9]。VCCT方法在模拟裂纹扩展时, 需要预先布置裂纹, 且在裂纹附近细分或不断重新划分网格。XFEM方法通过增加位移的富集项对间断项进行描述, 但其本身的收敛性较差。并且需要预先知道材料可能的破坏模式, 定义损伤后相应的开裂方向[9]。弥散的数值方法如近场动力学方法[10]、相场方法[11], 这些方法将裂纹弥散化, 描述裂纹的扩展过程。近场动力学方法将固体力学中的变形协调方程和力平衡方程改写为积分方程, 从而描述裂纹的萌生、扩展、分叉等问题[12-13]。然而, 该方法难以与材料的本构模型直接对应。
相场方法研究起源于1990年下半年, 从那时起, 就成为了一个重要的研究方向[14]。该方法通过引入一个场变量(序参数)——相场, 来描述系统中不同物理场之间的转变, 该变量在0和1之间变化, 分别表示材料的完好状态和完全破坏状态, 从而对裂纹的不连续性质进行描述。利用该方法可以模拟复杂的断裂过程, 如裂纹的萌生、扩展、分叉和结合等问题[15]。
目前, 分析材料失效的相场断裂模型主要分为2类: 第一类是以物理学中的Ginzburg-Landau理论为基础[16-17], 应用非约束裂纹相场的Ginzburg-Landau型演化方程和非凸衰减函数描述材料的损伤演化过程, 求解Ginzburg-Landau方程就可得到系统的位移场和损伤场。但该模型本质上是完全黏性的, 且主要适用于动态断裂[11]。第二类起源于断裂力学的变分方法, 是对经典Griffith断裂理论的延伸[18]。该理论由Francfort和Marigo[19]以及Bourdin等[20]提出, 采用变分方法和Γ收敛准则研究裂纹的演化过程, 使研究者更易于理解其力学概念和推向工程应用。该模型中用弹性势能和裂纹面能描述系统的总势能, 对其总势能求变分, 得到力平衡方程和损伤演化方程, 求解这2个方程, 得到位移场和损伤场, 该理论进一步由Miehe等[11]发展, 并建立了两类相场模型的统一。
Miehe等[21]又引入了历史场概念, 使裂纹相场演化满足不可逆约束, 为研究循环载荷下的裂纹扩展过程奠定了重要的理论基础, 并为相场理论的推广和应用做了重要铺垫, 使其能求解复杂的裂纹扩展问题。在Miehe等[21]研究基础上, 相场方法被不断改进并被应用到不同的研究领域。如脆性断裂问题[22-23]、塑性断裂问题[24-25]、动态断裂问题[26-27]、内聚力断裂问题[28-29]、材料疲劳问题[30-31]。同时, 研究材料范围也不断扩大, 如岩石类材料[32-33]、聚合物[34-35]、混凝土材料[36-37]、复合材料[38-39]。相比于其他的方法, 如XFEM法、界面单元法, 相场方法在研究材料失效过程中具有独特的优势, 使其能对不连续的裂纹进行描述, 以模拟复杂形式的裂纹扩展。
目前常用的相场模型主要有3种不同的选择类型, 即AT1和AT2模型, 以及PFM-CZM模型。对于AT1模型和PFM-CZM模型, 应力-应变关系存在线弹性阶段, 具有弹性极限应力, 即在载荷加载一段时间后, 才会出现损伤。而AT2模型[40], 采用常用的退化函数g2(d)=(1-d)2时, 应力-应变关系一直呈非线性形式, 不存在弹性极限, 即在载荷加载时损伤就立即发生, 并且在材料到达极限应力时, 损伤场已经增大到d=0.25, 在一定程度上影响了计算结果的准确性。为了使AT2模型更好地刻画材料的脆性断裂过程, 本文给出了一种通用的多项式型退化函数, 并分析退化函数对相场模型力学特性的影响。
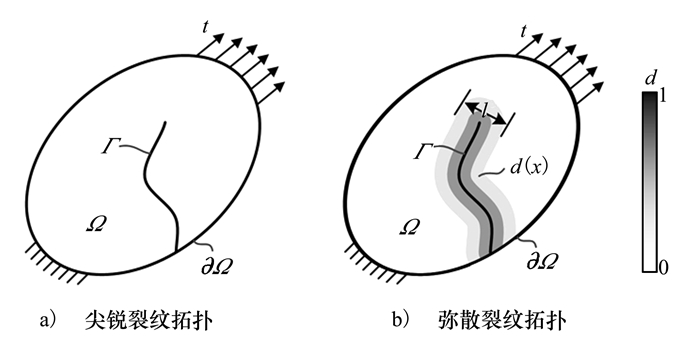
1 相场断裂模型 1.1 断裂能量泛函在相场模型中, 对于连续固体中的裂纹Γ, 可采用一个有限宽度l将裂纹弥散化, 使离散裂纹可以用某些连续函数模拟, 如图 1所示。这样就可引入辅助变量d(x)∈[0, 1]来描述这种尖锐裂纹, d=0表示杆的完好状态, d=1表示杆的完全断裂状态。
|
| 图 1 二维裂纹拓扑 |
这里, 可采用泛函[21]
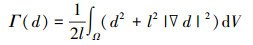
|
(1) |
表征尖锐的裂纹拓扑。裂纹面密度函数γ及其导数∂γ/∂d分别为
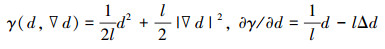
|
(2) |
对于图 1中的相场断裂问题, 根据(1)式中引入的断裂面函数Γ(d), 可定义产生新的裂纹拓扑所需的功

|
(3) |
式中, Gc是Griffith型临界能量释放率。
根据线弹性理论, 全局储能泛函可表示为

|
(4) |
储能函数ψ描述了单位体积中物体存储的体积能, 对于由断裂导致的能量降低, 可表示为

|
(5) |
式中, g(d)是能量退化函数, 应满足性质
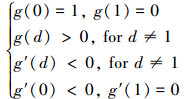
|
(6) |
参数k为残余刚度系数, 以保证数值的稳定性。ψ0为未损伤材料的应变能函数, 对于各向同性材料, 可表示为
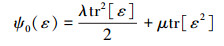
|
(7) |
为了保证裂纹扩展的准确性, 将应变能分解为正的部分ψ0+ (ε)和负的部分ψ0-(ε)
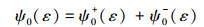
|
(8) |
式中: 依据Miehe等[21]的谱分解方法, ψ0+(ε)和ψ0-(ε)可分别表示为

|
(9) |
根据裂纹耗散泛函(3)式和储能泛函方程(4), 引入总的能量泛函
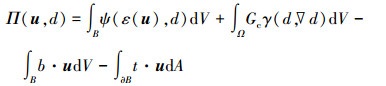
|
(10) |
式中: b是区域B中的体积力; t是在∂B上的表面外力。
对总能量泛函(10)式求变分, 可得到以下强形式的相场模型控制方程

|
(11) |
式中, 能量驱动力f为
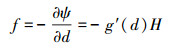
|
(12) |
为了保证损伤演化的不可逆性, 引入历史参考能量[21]
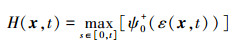
|
(13) |
为了模拟能量退化, 采用常用的多项式函数,如前文的g2(d), 以及三次函数[41]
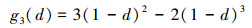
|
(14) |
和四次函数
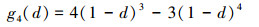
|
(15) |
采用g3(d)和g4(d)退化函数时, 都可使AT2相场模型得到弹性极限, 且其临界相场值分别为
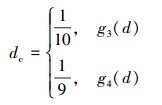
|
(16) |
这表明材料在达到极限应力时, 即发生脆性断裂时, 已经发生了一定程度的损伤, 且随着多项式次数的改变, 损伤程度发生了相应变化。
2.1 通用多项式型退化函数为了探究随着函数次数的改变, 退化函数对脆性断裂特性的影响, 采用一种通式来表达退化函数
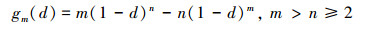
|
(17) |
根据退化函数性质((6)式), 可得到

|
(18) |
对于不同的m, gm(d)的变化趋势如图 2所示。

|
| 图 2 gm(d)随m变化形式 |
从图 2可以看出, 随着m的增大, 退化函数开始时平缓变化, 随后下降趋势逐渐增大, 在到达某个拐点后, 下降趋势开始变得缓慢, 表明在开始阶段材料性能下降缓慢, 然后下降趋势比较剧烈, 并在某个拐点后, 材料性能下降开始减缓。同时George等[42]也表示在材料开始发生损伤时, 由于材料内部微裂纹的相互作用和抑制, 在加载开始时, 材料损伤趋势较慢, 而在一定阶段后, 微裂纹间的相互阻止效应减弱, 损伤开始加快。因此, 采用这种多项式型退化函数, 在一定程度上与George等人的分析较为吻合。
对(17)式求导, 发现g′m(d=0)=0, 则能量驱动力

|
(19) |
这将使裂纹在开始阶段无法成核, 因此, 采用一种修正模型的退化函数

|
(20) |
当p=2, m=3, n=2时, g3(d)恢复为经典的退化函数g2(d)=(1-d)2。为了使相场模型在开始阶段存在裂纹驱动力, 裂纹能够成核, 需要将p设置为一个非零正值, 以保证在d=0时存在驱动力。
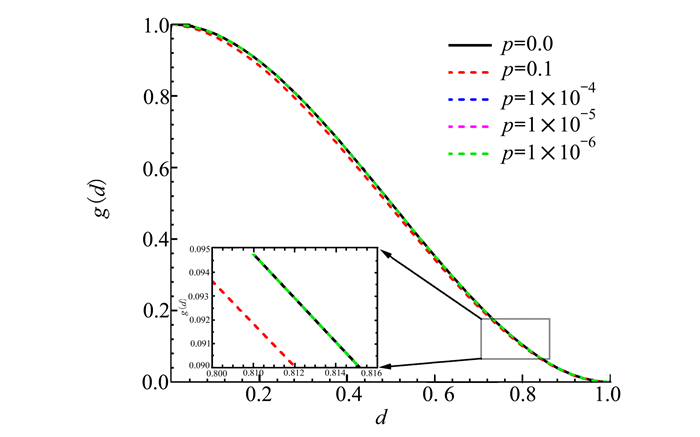
为了了解参数p对退化函数的影响, 假定m=3, 得到不同参数p时的gm(d)和g′m(d)曲线, 如图 3~4所示。
|
| 图 3 gm(d)随p的变化过程 |
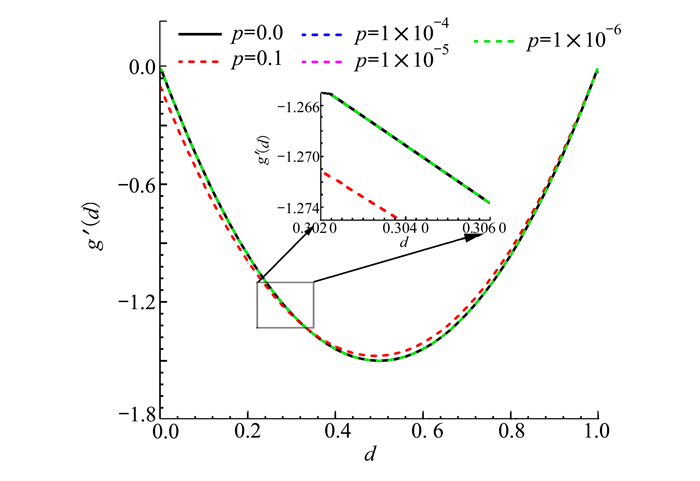
|
| 图 4 g′m(d)随p的变化过程 |
从图 3~4可以看出, 当p较大时, 如p=0.1, 退化函数(17)式和(20)式的计算结果存在一定差别, 而当0<p≪1时, 如p≤10-4, 退化函数(17)式和(20)式的计算结果基本一致, 说明当0<p≪1时, p对gm(d)的计算结果的影响很小。因此, 为了便于分析相场模型的力学特性, 在下文主要讨论p=0时的退化函数。对于p≠0情形, 见附录A。
2.2 均匀化解分析为了说明多项式型退化函数对相场断裂模型应力特性的影响, 下文将采用一维简单模型x∈[-L, L]分析相场断裂问题, 假定该模型区域中没有压缩应变场, 即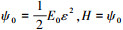
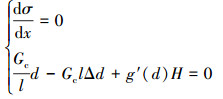
|
(21) |
式中, 应力为σ=g(d)E0ε。
忽略相场梯度Δd的影响, (21)式将变为
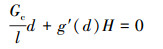
|
(22) |
将(20)式的导数代入(22)式可得到均匀化解
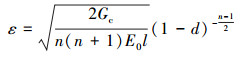
|
(23) |
在弹性极限处, 存在相场值

|
(24) |
将(24)式代入(23)式, 可得到弹性应变和应力极限
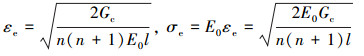
|
(25) |
将(23)式代入σ=g(d)E0ε, 并对d求导
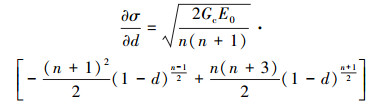
|
(26) |
当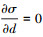

|
(27) |
从(27)式可以看出, 在多项式型退化函数中, 在n≥2情况下, 临界相场值恒满足dc>0, 这意味着材料在弹性阶段后, 还会存在一段非线性变化过程, 因此, 在到达脆性破坏极限时, 材料已经发生了一定程度的损伤。dc随n的变化形式如图 5所示。

|
| 图 5 临界相场值dc随着n的变化过程 |
从图 5可以看出, 随着n值的增大dc先增大后减小, 在n=3时, dc取得最大值, 且当n=2, 4时, 两者的临界相场值dc相等。这说明对于采用gm(d)的相场模型, 随着n的增大, 材料发生脆性断裂时的损伤程度先增大然后逐渐减小, 刻画脆性断裂的效果在增强。
将(27)式代入(23)式, 或者对σ=g(d)E0ε关于ε求导(见附录B), 都可得到临界应变
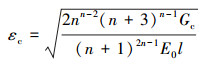
|
(28) |
因此, 可计算出临界应力

|
(29) |
为了表征弹性极限应力与临界应力特性的关系, 定义应力相对差值函数

|
(30) |
可得到应力相对差值随n变化的关系
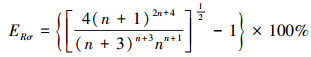
|
(31) |
如图 6所示。

|
| 图 6 应力特性随n的变化过程 |
从图 6可以看出, 随着n值的增大, 弹性极限应力与临界应力值都在减小, 但弹性极限应力减小的趋势小于与临界应力的减小趋势, 并且两者之间的相对差值在不断增大, 说明随着n值的增大, 相场模型的线弹性变化阶段在减弱, 非线性变化趋势在逐渐增强。
通过以上分析可知, 采用多项式型退化函数时, 在材料承受载荷后, 应力-应变首先呈线弹性变化, 然后是伴随着微小损伤的非线性变化, 在达到材料破坏极限时, 已经积累了一定程度的损伤。但相比较g2(d)函数, 这种多项式型函数能更好地描述材料脆性断裂过程。
3 相场模型数值实现 3.1 单元离散因为(11)式是关于位移场和相场的耦合方程, 通常采用多场有限元方法求解。首先对位移场u及其相应的应变场ε进行离散化
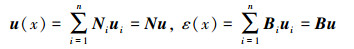
|
(32) |
式中, 插值矩阵N=[N1, …, Ni, …, Nn], 几何矩阵B=[B1, …, Bi, …, Bn]。
同理, 相场d及其相应的梯度场∇d可离散化为
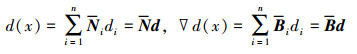
|
(33) |
相应的试探函数及其导数为
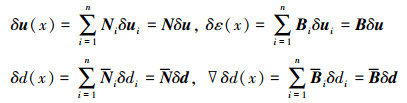
|
(34) |
其相应的容许函数类和试探函数类如(35)式所示
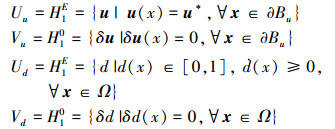
|
(35) |
然后, 可以得到以下弱形式的控制方程

|
(36) |
在求解(36)式时, 常用的方法有: 整体牛顿法、分步算法、BFGS法。而由于所得到的相场模型控制方程的非线性, 采用整体牛顿法计算时不容易收敛。为了改善计算的收敛性, 可采用分步算法求解以上的相场断裂模型控制方程, 但这种方法求解效率较慢, 计算复杂模型时非常耗时。由于BFGS法无需每次迭代都更新刚度矩阵, 且计算过程较为简单, 计算效率较高, 被Wu等[43]应用于控制方程的求解, 在保证收敛性的同时, 提高了计算效率。
对于弱耦合非线性问题, 通常可以忽略非对称项, 即
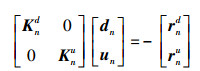
|
(37) |
求解方程(37)可得到位移场和相场。
式中
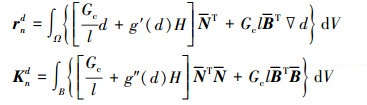
|
(38) |
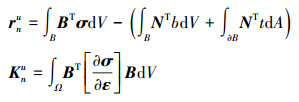
|
(39) |
由于不同次数的退化函数计算得到的弹性极限应力和临界应力不同, 而实际材料发生破坏时强度不会随退化函数发生变化, 因此, 可根据(29)式计算出不同退化函数计算时的长度尺度参数l。
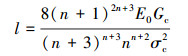
|
(40) |
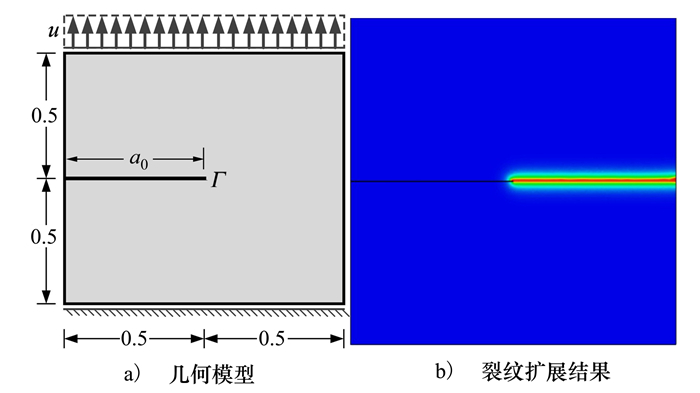
本节算例中模型尺寸为1 mm×1 mm, 在模型的中间区域0.5 mm的位置有一条初始裂纹Γ, 初始长度a0=0.5 mm, 下边界固定, 上边界施加拉伸载荷u=0.01 mm, 模型的边界条件及载荷形式如图 7所示, 其材料参数为E=210 kN/mm2, 泊松比ν=0.3, 能量释放率Gc=2.7×10-3 kN/mm。
|
| 图 7 几何模型及模拟结果 |
计算中模型最小单元尺度选择为h=0.5l, 假定n=2, 即m=3时, ln=2=0.01, 由于不同次数n时计算得到的临界应力相同, 因此根据(40)式可等效计算出n=3, 4, 5时的尺度参数l, ln=3=0.005 3, ln=4=0.003 3, ln=5=0.002 3。
从图 8可以看出, 相比于二次退化函数, 采用的多项式型退化函数使材料在断裂发生前更好地保持线弹性变化。在初始加载时, 由于材料内部微裂纹的相互抑制作用, 材料损伤增加地非常缓慢, 模型保持了线弹性变化, 很好地描述材料的脆性断裂性能, 如g3(d), g4(d)函数得到的载荷-位移曲线。

|
| 图 8 不同对应的载荷-位移曲线 |
同时, 从图 8可以发现, 随着多项式函数次数的增大, 由于其函数下降趋势逐渐增加, 材料内部微裂纹间的相互抑制效应减弱, 使材料损伤加快, 引起材料的断裂。所以虽然在计算中假定不同退化函数最终破坏的载荷相同, 即得到位移-载荷曲线应该相同, 但随着函数次数的增加, 其下降趋势增加, 即材料损伤趋势增大, 会诱发材料产生一定程度的微观损伤, 引起最终的断裂破坏, 如g5(d), g6(d)函数得到的载荷-位移曲线。通过该算例也说明了描述材料性能下降的退化函数, 其变化趋势在一定程度上也影响了材料损伤和断裂变化过程。
5 结论本文采用一种通用的多项式型退化函数分析了AT2相场断裂模型的力学特性, 通过研究得到了以下结论:
1) 通过一维简单模型分析得到了一般形式的弹性应变和应力、临界相场值等公式, 发现随着函数次数的增大, 临界相场值先增大, 然后减小, 表明当函数次数增大时, 理论上材料发生断裂时的损伤程度更小。
2) 相比于常用的二次退化函数, 多项式退化函数使相场模型具有弹性应力极限, 特别是当退化函数的次数较小时, 能很好地描述脆性断裂行为, 使材料在断裂前保持线弹性变化, 直至发生脆性断裂。
3) 退化函数的变化趋势会影响材料发生断裂的时间。在函数次数较小时, 如m=3, 4时, 模型断裂前很好地保持线弹性变化。随着函数次数的增大, 如m=5, 6时, 其函数下降趋势逐渐增加, 导致材料内部微裂纹间的相互抑制效应减弱, 诱发材料更早地发生损伤, 引起最终的断裂。但这种影响相比于二次退化函数, 还是比较微弱。
附录A当(20)式中的p≠0时, gm(d)、g′m(d)和g″m(d)分别为
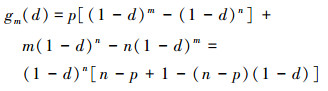
|
(41) |
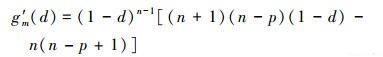
|
(42) |
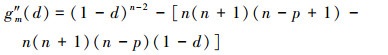
|
(43) |
由(22)式可得到应变
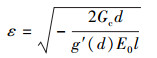
|
(44) |
对ε关于d求导, 得到
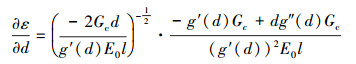
|
(45) |
对σ=g(d)E0ε关于d求导
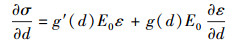
|
(46) |
将(45)式和(44)式代入(46)式
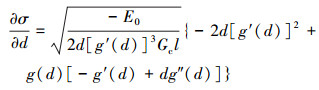
|
(47) |
当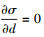

|
(48) |
将(41)~(43)式代入(48)式, 得到
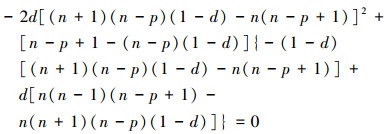
|
(49) |
整理化简可得到一个关于d的三次多项式, 但由于多项式较为复杂, 此处不再展示, 利用Matlab或者Mathematica求解(49)式, 可得到一个关于n, p的多项式
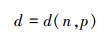
|
(50) |
将退化函数带入应力表达式σ=g(d)E0ε中, 得到
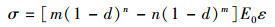
|
(51) |
将(23)式代入(51)式, 可得到
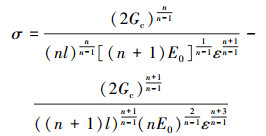
|
(52) |
对(52)式关于ε求导得
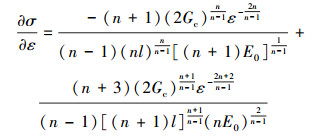
|
(53) |
使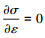
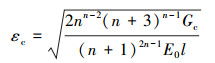
|
(54) |
如(28)式所示。
| [1] | ARSON C. Generalized stress variables in continuum damage mechanics[J]. Mechanics Research Communications, 2014, 60: 81-84. DOI:10.1016/j.mechrescom.2014.06.006 |
| [2] | ZHAN Z, HU W, LI B, et al. Continuum damage mechanics combined with the extended finite element method for the total life prediction of a metallic component[J]. International Journal of Mechanical Sciences, 2017, 124/125: 48-58. DOI:10.1016/j.ijmecsci.2017.03.002 |
| [3] | PANDEY V B, SAMANT S S, SINGH I V, et al. An improved methodology based on continuum damage mechanics and stress triaxiality to capture the constraint effect during fatigue crack propagation[J]. International Journal of Fatigue, 2020, 140: 105823. DOI:10.1016/j.ijfatigue.2020.105823 |
| [4] | DAVEY K, DARVIZEH R, ZHANG J. Finite similitude in fracture mechanics[J]. Engineering Fracture Mechanics, 2021, 245: 107573. DOI:10.1016/j.engfracmech.2021.107573 |
| [5] | YUN K, WANG Z, RONALD S, et al. An advanced continuum damage mechanics model for predicting the crack progress process based on the consideration of the influence of crack direction under quasi-static load[J]. International Journal of Mechanical Sciences, 2017, 130: 487-496. DOI:10.1016/j.ijmecsci.2017.05.021 |
| [6] | FRANCISCO E J, JOSÉ F. A novel continuum damage model to simulate quasi-brittle failure in mode I and mixed-mode conditions using a continuous or a continuous-discontinuous strategy[J]. Theoretical and Applied Fracture Mechanics, 2020, 109: 102745. DOI:10.1016/j.tafmec.2020.102745 |
| [7] | JIANG S, GU Y, FAN C M, et al. Fracture mechanics analysis of bimaterial interface cracks using the generalized finite difference method[J]. Theoretical and Applied Fracture Mechanics, 2021, 113: 102942. DOI:10.1016/j.tafmec.2021.102942 |
| [8] | KRUEGER R. Virtual crack closure technique: history, approach, and applications[J]. Applied Mechanics Reviews, 2004, 57(1): 109-143. |
| [9] | MOES N, DOLBOW J, BELYTSCHKO T. A finite element method for crack growth without remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 46: 131-150. DOI:10.1002/(SICI)1097-0207(19990910)46:1<131::AID-NME726>3.0.CO;2-J |
| [10] | BOBARU F, FOSTER J T, GEUBELLE P H, et al. Handbook of Peridynamic Modeling[M]. Boca Raton: CRC Press, 2016. |
| [11] | MIEHE C, WELSCHINGER F, HOFACKER M. Thermodynamically-consistent phase field models of fracture: variational principles and multi-field FE implementations[J]. International Journal for Numerical Methods in Engineering, 2010, 83: 1273-1311. DOI:10.1002/nme.2861 |
| [12] | SILLING S, EPTON M, WECKNERO O, et al. Peridynamics states and constitutive modeling[J]. Journal of Elasticity, 2007, 88: 151-184. DOI:10.1007/s10659-007-9125-1 |
| [13] | SILLING S. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids, 2000, 48: 175-209. DOI:10.1016/S0022-5096(99)00029-0 |
| [14] | AMBATI M, GERASIMOV T, LORENZIS L D. A review on phase-field models of brittle fractureand a new fast hybrid formulation[J]. Computational Mechanics, 2015, 55: 383-405. DOI:10.1007/s00466-014-1109-y |
| [15] | TEICHTMEISTER S, KIENLE D, ALDAKHEEL F, et al. Phase field modeling of fracture in anisotropic brittle solids[J]. International Journal of Non-Linear Mechanics, 2017, 97: 1-21. DOI:10.1016/j.ijnonlinmec.2017.06.018 |
| [16] | HAKIM V, KARMA A. Laws of crack motion and phase-field models of fracture[J]. Journal of the Mechanics and Physics of Solids, 2009, 57: 342-368. DOI:10.1016/j.jmps.2008.10.012 |
| [17] | PONS A J, KARMA A. Helical crack-front instability in mixed-mode fracture[J]. Nature, 2010, 464(7285): 85-89. DOI:10.1038/nature08862 |
| [18] | BOURDIN B, FRANCFORT G, MARIGO J J. The variational approach to fracture[M]. Berlin: Springer Science+Business Media, 2008. |
| [19] | FRANCFORT G A, MARIGO J J. Revisiting brittle fracture as an energy minimization problem[J]. Journal of the Mechanics and Physics of Solids, 1998, 46: 1319-1342. DOI:10.1016/S0022-5096(98)00034-9 |
| [20] | BOURDIN B, FRANCFORT G A, MARIGO J J. Numerical experiments in revisited brittle fracture[J]. Journal of the Mechanics and Physics of Solids, 2000, 48: 797-826. DOI:10.1016/S0022-5096(99)00028-9 |
| [21] | MIEHE C, HOFACKER M, WELSCHINGER F. A phase field model for rate-independent crack propagation: robust algorithmic implementation based on operator splits[J]. Computer Method in Applied Mechanics and Engineering, 2010, 199: 2765-2778. DOI:10.1016/j.cma.2010.04.011 |
| [22] | CHEN Y, VASIUKOV D, GÉLÉBART L, et al. A FFT solver for variational phase-field modeling of brittle fracture[J]. Computer Method in Applied Mechanics and Engineering, 2019, 349: 167-190. DOI:10.1016/j.cma.2019.02.017 |
| [23] | HIRSHIKESH, PRAMOD A L N, ANNABATTULA R K, et al. Adaptive phase-field modeling of brittle fracture using the scaled boundary finite element method[J]. Computer Method in Applied Mechanics and Engineering, 2019, 355: 284-307. DOI:10.1016/j.cma.2019.06.002 |
| [24] | MIEHE C, HOFACKER M, SCHÄNZEL LM, et al. Phase field modeling of fracture in multi-physics problems. Part Ⅱ. Coupled brittle-to-ductile failure criteria and crack propagation in thermo-elastic-plastic solids[J]. Computer Method in Applied Mechanics and Engineering, 2015, 294: 486-522. DOI:10.1016/j.cma.2014.11.017 |
| [25] | BORDEN M J, HUGHES T J, LANDIS C M, et al. A phase-field formulation for fracture in ductile materials: finite deformation balance law derivation, plastic degradation, and stress triaxiality effects[J]. Computer Method in Applied Mechanics and Engineering, 2016, 312: 130-166. DOI:10.1016/j.cma.2016.09.005 |
| [26] | BORDEN M J, VERHOOSEL C V, SCOTT M A, et al. A phase-field description of dynamic brittle fracture[J]. Computer Method in Applied Mechanics and Engineering, 2012, 217/218/219/220: 77-95. |
| [27] | REN H, ZHUANG X, ANITESCU C, et al. An explicit phase field method for brittle dynamic fracture[J]. Computers and Structures, 2019, 217: 45-56. DOI:10.1016/j.compstruc.2019.03.005 |
| [28] | PAGGI M, REINOSO J. Revisiting the problem of a crack impinging on an interface: a modeling framework for the interaction between the phase field approach for brittle fracture and the interface cohesive zone model[J]. Computer Method in Applied Mechanics and Engineering, 2017, 321: 145-172. DOI:10.1016/j.cma.2017.04.004 |
| [29] | MANDAL T K, NGUYEN V P, WU J Y. Length scale and mesh bias sensitivity of phase-field models for brittle and cohesive fracture[J]. Engineering Fracture Mechanics, 2019, 217: 106532. DOI:10.1016/j.engfracmech.2019.106532 |
| [30] | MESGARNEJAD A, IMANIAN A, KARMA A. Phase-field models for fatigue crack growth[J]. Theoretical and Applied Fracture Mechanics, 2019, 103: 102282. DOI:10.1016/j.tafmec.2019.102282 |
| [31] | LO Y S, BORDEN M J, RAVI-CHANDAR K, et al. A phase-field model for fatigue crack growth[J]. Journal of the Mechanics and Physics of Solids, 2019, 132: 103684. DOI:10.1016/j.jmps.2019.103684 |
| [32] | BRYANT E C, SUN W C. A mixed-mode phase field fracture model in anisotropic rocks with consistent kinematics[J]. Computer Method in Applied Mechanics and Engineering, 2018, 342: 561-584. DOI:10.1016/j.cma.2018.08.008 |
| [33] | ZHOU S, ZHUANG X, RABCZUK T. Phase field modeling of brittle compressive-shear fractures in rock-like materials: a new driving force and a hybrid formulation[J]. Computer Method in Applied Mechanics and Engineering, 2019, 355: 729-752. DOI:10.1016/j.cma.2019.06.021 |
| [34] | XIE Y, KRAVCHENKO OG, PIPES RB, et al. Phase field modeling of damage in glassy polymers[J]. Journal of the Mechanics and Physics of Solids, 2016, 93: 182-197. DOI:10.1016/j.jmps.2015.12.021 |
| [35] | TALAMINI B, MAO Y, ANAND L. Progressive damage and rupture in polymers[J]. Journal of the Mechanics and Physics of Solids, 2018, 111: 434-457. DOI:10.1016/j.jmps.2017.11.013 |
| [36] | FENG D C, WU J Y. Phase-field regularized cohesive zone model (CZM) and size effect of concrete[J]. Engineering Fracture Mechanics, 2018, 197: 66-79. DOI:10.1016/j.engfracmech.2018.04.038 |
| [37] | YANG Z J, LI B B, WU J Y. X-ray computed tomography images based phase-field modeling of mesoscopic failure in concrete[J]. Engineering Fracture Mechanics, 2019, 208: 151-170. DOI:10.1016/j.engfracmech.2019.01.005 |
| [38] | ESPADAS E J J, DIJK N P V, ISAKSSON P. A phase-field model for strength and fracture analyses of fiber-reinforced composites[J]. Composites Science and Technology, 2019, 174: 58-67. DOI:10.1016/j.compscitech.2018.10.031 |
| [39] | QUINTANAS C A, REINOSO J, CASONIC E, et al. A phase field approach to simulate intralaminar and translaminar fracture in long fiber composite materials[J]. Composite Structures, 2019, 220: 899-911. DOI:10.1016/j.compstruct.2019.02.007 |
| [40] | LIU G, LI Q, MSEKH M A, et al. Abaqus implementation of monolithic and staggered schemes for quasi-static and dynamic fracture phase-field model[J]. Computational Materials Science, 2016, 121: 35-47. DOI:10.1016/j.commatsci.2016.04.009 |
| [41] | KUHN C, SCHLVTER A, MVLLER R. On degradation functions in phase field fracture models[J]. Computational Materials Science, 2015, 108: 374-384. DOI:10.1016/j.commatsci.2015.05.034 |
| [42] | GEORGE Z V, NAVID M. Nonlocal damage model using the phase field method: theory and applications[J]. International Journal of Solids and Structures, 2013, 50: 3136-3151. DOI:10.1016/j.ijsolstr.2013.05.015 |
| [43] | WU J Y, HUANG Y, NGUYEN P V. On the BFGS monolithic algorithm for the unified phase field damage theory[J]. Computer Method in Applied Mechanics and Engineering, 2020, 360: 112704. DOI:10.1016/j.cma.2019.112704 |
2. School of Astronautics, Northwestern Polytechnical University, Xi'an 710072, China;
3. Xi'an Modern Control Technology Research Institute, Xi'an 710065, China




